OpenCascade Shape Representation in OpenSceneGraph
eryar@163.com
摘要Abstract:本文通過程序實例,將OpenCascade中的拓樸數據(邊、面)離散化后在OpenSceneGraph中進行顯示。有了這些離散數據,就可以不用OpenCascade的顯示模塊了,可以使用其他顯示引擎對形狀進行顯示。即若要線框模式顯示形狀時,就繪制離散形狀拓樸邊后得到的多段線;若要實體渲染模式顯示形狀時,就繪制離散形狀拓樸面得到的三角網格。理解這些概念也有助于理解顯示模塊的實現,及拓樸數據中包含的幾何數據的意義。
關鍵字 Key Words:OpenCascade, polygon curve, triangulation,discrete edge, discrete face, OpenSceneGraph, OSG
一、引言 Introduction
“實體造型技術主流的是邊界表達BRep,就是模型由面和邊組成,這些面和邊都是參數化的解析曲面和曲線,當拉伸或切割實體操作時候,就是用生成的實體和已有的實體進行實體布爾運算,其實是進行的面和邊的相交運算,從而算出到新的面或者邊。比如圓柱面和平面相交,以前的圓柱面分成了兩個,同時產生出一條相交的空間橢圓曲線段,這些解析面/線邊要通過三角化算法離散成三角網格或者線段條作為逼近表達,才能用OpenGL畫出來。”以上內容來自博客:http://yrcpp.blog.163.com/blog/static/126045259201310199515969/ ,感謝網友的分享,言簡意賅地把造型的核心進行了說明。
以前看《計算機圖形學》相關的書時,從數學概念到具體實現的橋梁總是無法銜接。現在,通過學習OpenCascade,終于把這些都串起來了。正如上面網友所說,面和邊要在OpenGL中顯示出來就需要離散化,即把邊離散為多段線,把面離散為三角網格。這樣就可以把用參數精確表示的幾何數據在計算機布滿像素點的屏幕上逼近顯示了。
本文通過程序實例,將OpenCascade中的拓樸數據(邊、面)離散化后在OpenSceneGraph中進行顯示。有了這些離散數據,就可以不用OpenCascade的顯示模塊了,可以使用其他顯示引擎對形狀進行顯示。即若要線框模式顯示形狀時,就繪制離散形狀拓樸邊后得到的多段線;若要實體渲染模式顯示形狀時,就繪制離散形狀拓樸面得到的三角網格。理解這些概念也有助于理解顯示模塊的實現,及拓樸數據中包含的幾何數據的意義。
二、程序示例
以下通過一個具體程序實例,來對OpenCascade中的拓樸邊和拓樸面進行離散化。
/*
* Copyright (c) 2013 eryar All Rights Reserved.
*
* File : Main.cpp
* Author : eryar@163.com
* Date : 2013-12-03 18:09
* Version : 1.0v
*
* Description : Draw OpenCascade polygon Curves of the edge
* and triangulations of the face in OpenSceneGraph.
* When you want to display the shape in the computer,
* you can not display the geometry exactly, the only
* way to show them is in the approximation form.
*
* Key Words : OpenCascade, polygon curve, triangulation,
* discrete edge, discrete face, OpenSceneGraph, OSG
*
*/
// OpenCascade library.
#define WNT
#include <gp_Circ.hxx>
#include <gp_Elips.hxx>
#include <gp_Sphere.hxx>
#include <Poly_Polygon3D.hxx>
#include <Poly_Triangulation.hxx>
#include <TopoDS_Edge.hxx>
#include <TopoDS_Face.hxx>
#include <BRep_Tool.hxx>
#include <BRepMesh.hxx>
#include <BRepBuilderAPI_MakeEdge.hxx>
#include <BRepBuilderAPI_MakeFace.hxx>
#pragma comment(lib, "TKernel.lib")
#pragma comment(lib, "TKMath.lib")
#pragma comment(lib, "TKBRep.lib")
#pragma comment(lib, "TKMesh.lib")
#pragma comment(lib, "TKTopAlgo.lib")
// OpenSceneGraph library.
#include <osgDB/ReadFile>
#include <osgViewer/Viewer>
#include <osgGA/StateSetManipulator>
#include <osgViewer/ViewerEventHandlers>
#pragma comment(lib, "osgd.lib")
#pragma comment(lib, "osgDBd.lib")
#pragma comment(lib, "osgGAd.lib")
#pragma comment(lib, "osgViewerd.lib")
/*
* @breif Descret the shape: edge.
* For Edge will be discreted to polylines; (GCPnts_TangentialDeflection)
* To get the polyline of the edge, use BRep_Tool::Polygon3D(Edge, L);
*/
osg::Node* BuildPolyline(const TopoDS_Edge& edge, double deflection = 0.1)
{
osg::ref_ptr<osg::Geode> geode = new osg::Geode();
osg::ref_ptr<osg::Geometry> linesGeom = new osg::Geometry();
osg::ref_ptr<osg::Vec3Array> pointsVec = new osg::Vec3Array();
TopLoc_Location location;
BRepMesh::Mesh(edge, deflection);
Handle_Poly_Polygon3D polyline = BRep_Tool::Polygon3D(edge, location);
for (int i = 1; i < polyline->NbNodes(); i++)
{
gp_Pnt point = polyline->Nodes().Value(i);
pointsVec->push_back(osg::Vec3(point.X(), point.Y(), point.Z()));
}
// Set the color of the polyline.
osg::ref_ptr<osg::Vec4Array> colors = new osg::Vec4Array;
colors->push_back(osg::Vec4(1.0f, 1.0f, 0.0f, 0.0f));
linesGeom->setColorArray(colors.get());
linesGeom->setColorBinding(osg::Geometry::BIND_OVERALL);
// Set vertex array.
linesGeom->setVertexArray(pointsVec);
linesGeom->addPrimitiveSet(new osg::DrawArrays(osg::PrimitiveSet::LINE_LOOP, 0, pointsVec->size()));
geode->addDrawable(linesGeom.get());
return geode.release();
}
/*
* @breif Descret the shape: face.
* For Face will be discreted to triangles; (BRepMesh_FastDiscret)
* To get the triangles of the face, use BRep_Tool::Triangulation(Face, L);
*/
osg::Node* BuildMesh(const TopoDS_Face& face, double deflection = 0.1)
{
osg::ref_ptr<osg::Geode> geode = new osg::Geode();
osg::ref_ptr<osg::Geometry> triGeom = new osg::Geometry();
osg::ref_ptr<osg::Vec3Array> vertices = new osg::Vec3Array();
osg::ref_ptr<osg::Vec3Array> normals = new osg::Vec3Array();
TopLoc_Location location;
BRepMesh::Mesh(face, deflection);
Handle_Poly_Triangulation triFace = BRep_Tool::Triangulation(face, location);
Standard_Integer nTriangles = triFace->NbTriangles();
gp_Pnt vertex1;
gp_Pnt vertex2;
gp_Pnt vertex3;
Standard_Integer nVertexIndex1 = 0;
Standard_Integer nVertexIndex2 = 0;
Standard_Integer nVertexIndex3 = 0;
TColgp_Array1OfPnt nodes(1, triFace->NbNodes());
Poly_Array1OfTriangle triangles(1, triFace->NbTriangles());
nodes = triFace->Nodes();
triangles = triFace->Triangles();
for (Standard_Integer i = 1; i <= nTriangles; i++)
{
Poly_Triangle aTriangle = triangles.Value(i);
aTriangle.Get(nVertexIndex1, nVertexIndex2, nVertexIndex3);
vertex1 = nodes.Value(nVertexIndex1).Transformed(location.Transformation());
vertex2 = nodes.Value(nVertexIndex2).Transformed(location.Transformation());
vertex3 = nodes.Value(nVertexIndex3).Transformed(location.Transformation());
gp_XYZ vector12(vertex2.XYZ() - vertex1.XYZ());
gp_XYZ vector13(vertex3.XYZ() - vertex1.XYZ());
gp_XYZ normal = vector12.Crossed(vector13);
Standard_Real rModulus = normal.Modulus();
if (rModulus > gp::Resolution())
{
normal.Normalize();
}
else
{
normal.SetCoord(0., 0., 0.);
}
//if (face.Orientable() != TopAbs_FORWARD)
//{
// normal.Reverse();
//}
vertices->push_back(osg::Vec3(vertex1.X(), vertex1.Y(), vertex1.Z()));
vertices->push_back(osg::Vec3(vertex2.X(), vertex2.Y(), vertex2.Z()));
vertices->push_back(osg::Vec3(vertex3.X(), vertex3.Y(), vertex3.Z()));
normals->push_back(osg::Vec3(normal.X(), normal.Y(), normal.Z()));
}
triGeom->setVertexArray(vertices.get());
triGeom->addPrimitiveSet(new osg::DrawArrays(osg::PrimitiveSet::TRIANGLES, 0, vertices->size()));
triGeom->setNormalArray(normals);
triGeom->setNormalBinding(osg::Geometry::BIND_PER_PRIMITIVE);
geode->addDrawable(triGeom);
return geode.release();
}
osg::Node* BuildScene(void)
{
osg::ref_ptr<osg::Group> root = new osg::Group();
gp_Ax2 axis;
// 1. Test circle while deflection is default 0.1;
TopoDS_Edge circleEdge1 = BRepBuilderAPI_MakeEdge(gp_Circ(axis, 6.0));
root->addChild(BuildPolyline(circleEdge1));
// 2. Test circle while deflection is 0.001.
axis.SetLocation(gp_Pnt(8.0, 0.0, 0.0));
axis.SetDirection(gp_Dir(1.0, 1.0, 1.0));
TopoDS_Edge circleEdge2 = BRepBuilderAPI_MakeEdge(gp_Circ(axis, 6.0));
root->addChild(BuildPolyline(circleEdge2, 0.001));
// 3. Test ellipse while deflection is 1.0.
TopoDS_Edge ellipseEdge = BRepBuilderAPI_MakeEdge(gp_Elips(gp::XOY(), 16.0, 8.0));
root->addChild(BuildPolyline(ellipseEdge, 1.0));
// 4. Test sphere face while deflection is default 0.1.
axis.SetLocation(gp_Pnt(26.0, 0.0, 0.0));
TopoDS_Face sphereFace1 = BRepBuilderAPI_MakeFace(gp_Sphere(axis, 8.0));
root->addChild(BuildMesh(sphereFace1));
// 5. Test sphere face while deflection is 2.0.
axis.SetLocation(gp_Pnt(26.0, 18.0, 0.0));
TopoDS_Face sphereFace2 = BRepBuilderAPI_MakeFace(gp_Sphere(axis, 8.0));
root->addChild(BuildMesh(sphereFace2, 2.0));
// 6. Test sphere face while deflection is 0.001.
axis.SetLocation(gp_Pnt(26.0, -18.0, 0.0));
TopoDS_Face sphereFace3 = BRepBuilderAPI_MakeFace(gp_Sphere(axis, 8.0));
root->addChild(BuildMesh(sphereFace3, 0.001));
return root.release();
}
int main(void)
{
osgViewer::Viewer myViewer;
myViewer.setSceneData(BuildScene());
myViewer.addEventHandler(new osgGA::StateSetManipulator(myViewer.getCamera()->getOrCreateStateSet()));
myViewer.addEventHandler(new osgViewer::StatsHandler);
myViewer.addEventHandler(new osgViewer::WindowSizeHandler);
return myViewer.run();
}
示例程序測試了不同的離散精度情況下同一個形狀的顯示效果,程序結果如下圖所示:
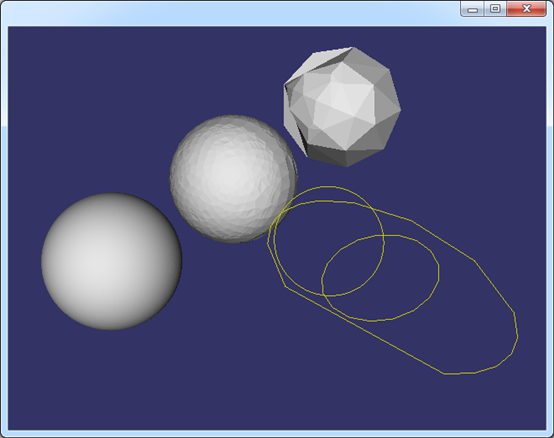
Figure 2.1 Edge and Face representation in OpenSceneGraph
從圖中可知,離散精度越高,離散后得到線上的點或三角網格就越多,顯示越細膩。
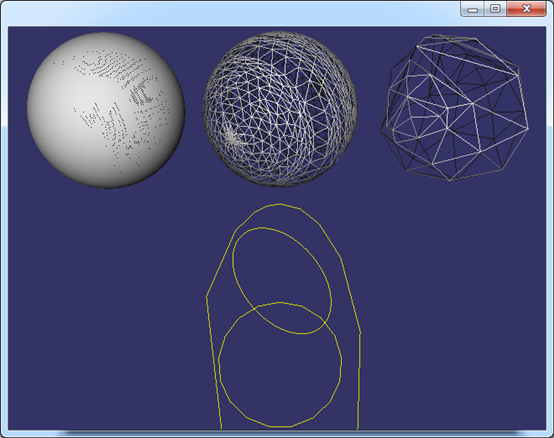
Figure 2.2 Edge and Face representation in OpenSceneGraph
其中,邊的離散化使用到了類:GCPnts_TangentialDeflection;面的離散化使用到了類:BRepMesh_FastDiscret。有興趣的讀者可跟蹤調試,理解其具體實現的算法。邊的離散應該很好理解,面的離散使用了Delauney三角剖分算法。關于Delauney三角剖分算法的介紹可參考博客:http://www.shnenglu.com/eryar/archive/2013/05/26/200605.aspx。
三、結論
通過把OpenCascade中的拓樸邊和面離散化用OpenSceneGraph顯示,填補了形狀數學精確表示與在計算機屏幕上近似顯示之間的隔閡。也有助于理解拓樸結構中包含幾何數據的BRep_TFace、BRep_TEdge、BRep_TVertex中除了包含面、邊的精確的參數表示數據外,還包含了用于近似顯示的離散數據的意義。
四、參考資料
1. 博客:http://yrcpp.blog.163.com/blog/static/126045259201310199515969/
2. 博客:http://www.shnenglu.com/eryar/archive/2013/05/26/200605.aspx