Seam Edge and Degenerated Edge
eryar@163.com
摘要Abstract:介紹了ACIS與OpenCascade中的Seam edge和Degenerated edge。通過對比學習,更好地理解了Seam Edge和Degenerated Edge的概念。
關鍵字Key Words:ACIS、OpenCascade、Seam Edge、Degenerated Edge
一、Seam Edge and Degenerated Edge in OpenCascade
最近在看OpenCascade中的拓樸與幾何(Topology and Geometry),發現他對拓樸邊進行了分類,其中有強調了兩種特殊種類的邊:seam-edge和degenerated edge。在Roman Lygin的博客對其定義分別為:
l Seam edge:one which is shared by the same face twice(i.e. Has 2 pcurves on the same surface).
l Degenerated edge:one which lies on a surface singularity that corresponds to a single point in 3D space.
并以球面為例說明了這兩種邊,關于球面的seam edge和degenerated edge如下圖所示:
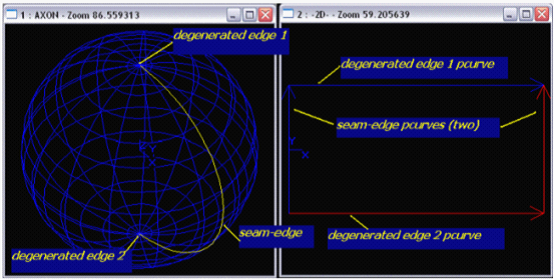
Figure 1.1 Seam edge and degenerated edge of sphere
Other examples - torus, cylinder, and cone. Torus has two seam-edge corresponding to its parametric space boundaries; cylinder has a seam-edge. Degenerated edge represents on a cone apex.
根據其定義,在看《基于ACIS的幾何造型技術與系統開發》時,發現ACIS中也有相同的概念。通過對比學習,更好地理解了seam-edge和degenerated edge的概念。下面從《基于ACIS的幾何造型技術與系統開發》書中摘抄一些內容來說明這兩個概念。
二、Seam Edge and Degenerated Edge in ACIS
在ACIS中,樣條曲面也被稱為參數曲面,是從二維參數空間到三維模型空間的映射,如圖所示:
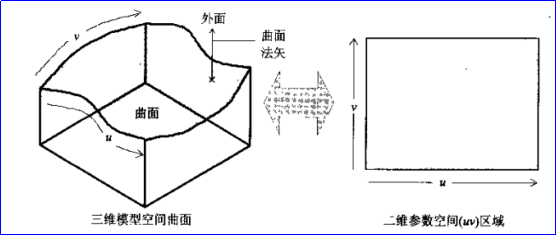
Figure 2.1 Parametric surface
參數空間的矩形區域中的兩個對邊可以映射成模型空間中的同一條邊,如圖2.2和圖2.3中圓柱和圓錐的銜接線。在這種情況下,曲面在與這些垂直的參數方向是閉合的。如果在這個邊界上曲面的參數化方程的導數也相等,那么該曲面在這個參數方向上為周期曲面(Periodic surface)。模型空間中與該邊對應的直線為周期曲面的銜接線(seam line)。如圖2.2所示,圓柱在一個方向上具有周期懷而在另一個方向上不具備周期性,圓環面在兩個方向都具有周期性。
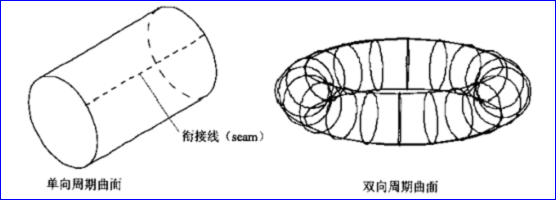
Figure 2.2 Periodic surface
參數空間的矩形區域的一邊可以映射成一個模型空間中的單一點,如圖2.3所示,該點是曲面的一個參數奇異點,如果曲面在這一點的法線不連續,這個點就是曲面的奇異點。在OpenCascade類似描述的為Degenerated edge。
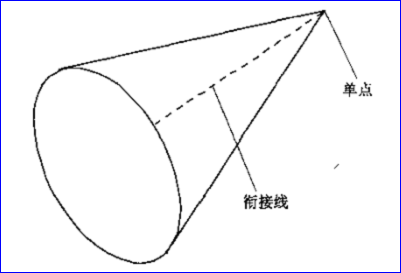
Figure 2.3 參數邊映射成單一點
三、參考資料
1. 詹海生等, 基于ACIS的幾何造型技術與系統開發, 清華大學出版社, 2002
2. Roman Lygin, OpenCascade notes, opencascade.blogspot.com