Topology and Geometry in OpenCascade-Vertex
eryar@163.com
摘要Abstract：本文簡(jiǎn)要介紹了幾何造型中的邊界表示法（BRep），并結(jié)合程序說(shuō)明OpenCascade中的邊界表示的具體實(shí)現(xiàn)，即拓樸與幾何的聯(lián)系。對(duì)具有幾何信息的拓樸結(jié)構(gòu)頂點(diǎn)（vertex）、邊（edge）、面（face）進(jìn)行了詳細(xì)說(shuō)明。本文只對(duì)頂點(diǎn)數(shù)據(jù)進(jìn)行說(shuō)明。
關(guān)鍵字Key Words：OpenCascade、BRep、Topology、Geometry
一、引言 Introduction
邊界表示（Boundary Representation）也稱為BRep表示，它是幾何造型中最成熟、無(wú)二義的表示法。實(shí)體的邊界通常是由面的并集來(lái)表示，而每個(gè)面又由它所在的曲面的定義加上其邊界來(lái)表示，面的邊界是邊的并集，而邊又是由點(diǎn)來(lái)表示的。
邊界表示的一個(gè)重要特征是描述形體的信息包括幾何信息（Geometry）和拓樸信息（Topology）兩個(gè)方面。拓樸信息描述形體上的頂點(diǎn)、邊、面的連接關(guān)系，它形成物體邊界表示的“骨架”。形體的幾何信息猶如附著在“骨架”上的肌肉。例如，形體的某個(gè)面位于某一個(gè)曲面上，定義這一曲面方程的數(shù)據(jù)就是幾何信息。此外，邊的形狀、頂點(diǎn)在三維空間中的位置（點(diǎn)的坐標(biāo)）等都是幾何信息，一般來(lái)說(shuō)，幾何信息描述形體的大小、尺寸、位置和形狀等。
在邊界表示法中，邊界表示就按照體－面－環(huán)－邊－點(diǎn)的層次，詳細(xì)記錄構(gòu)成形體的所有幾何元素的幾何信息及其相互連接的拓樸關(guān)系。這樣，在進(jìn)行各種運(yùn)算和操作中，就可以直接取得這些信息。
下圖所示為由一條邊連接的兩個(gè)面組成的殼（shell）：
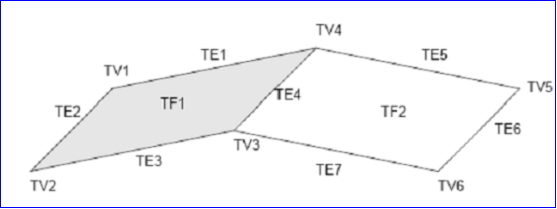
Figure 1.1 Structure of a shell formed from two faces
上圖所示的形狀表示為TS， 面TF1和TF2，有七條邊TE1~TE7和六個(gè)頂點(diǎn)TV1~TV6。
環(huán)TW1引用邊TE1~TE4；環(huán)TW2引用TE4~TE7 。邊引用的頂點(diǎn)如下：TE1（TV1，TV4），TE2（TV1，TV2），TE3（TV2，TV3），TE4（TV3，TV4），TE5（TV4，TV5），TE6（TV5，TV6），TE7（TV3，TV6）。
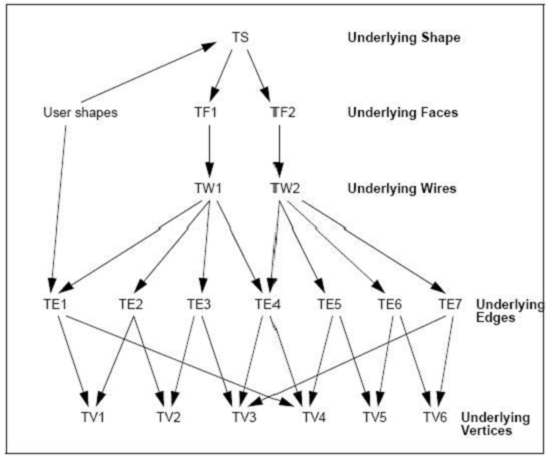
Figure 1.2 Data structure of the shell formed from two faces connected at an edge
注：OpenCascade中的這個(gè)數(shù)據(jù)結(jié)構(gòu)中不包含“回溯引用（back references）”，即所有的引用只從復(fù)雜形狀到簡(jiǎn)單形狀。（Note that this data structure does not contain any “back references”. All references go from more comples underlying shapes to less complex ones.）有點(diǎn)有向圖的意思。
二、OpenCascade中的邊界表示 BRep in OpenCascade
2.1 拓樸結(jié)構(gòu) TopoDS_Shape data structure
OpenCascade中的拓樸（topology）是根據(jù)STEP標(biāo)準(zhǔn)ISO-10303-42設(shè)計(jì)的。也許讀一下這個(gè)標(biāo)準(zhǔn)中的有關(guān)概念還是很有幫助的。STEP ISO-10303-42的相關(guān)資源：
http://www.steptools.com/support/stdev_docs/express/step_irs/index.html
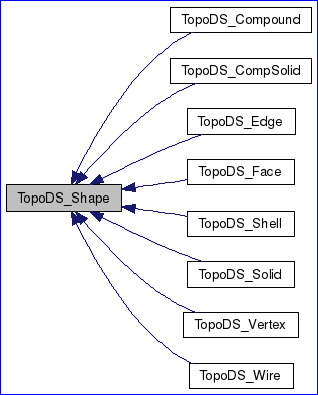
Figure 2.1 Topology data structure in OpenCascade
TopoDS_Shape由值控制，包含三個(gè)成員變量：myLocation、myOrient、myTShape。
Figure 2.2 TopoDS_Shape member fields
2.2 拓樸與幾何的聯(lián)系 Connection with Geometry
現(xiàn)在我們來(lái)考慮一下拓樸結(jié)構(gòu)與幾何的關(guān)系。通過(guò)繼承TopoDS包中的抽象的拓樸類實(shí)現(xiàn)了邊界表示模型。如下圖所示：
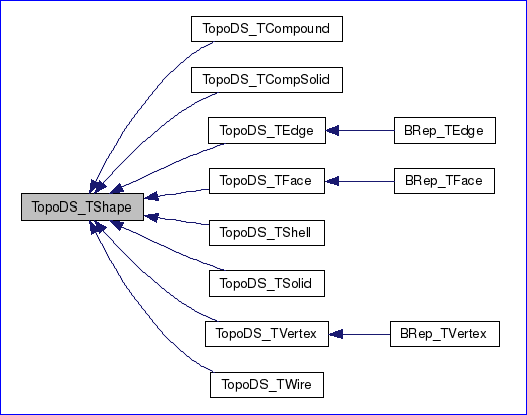
Figure 2.3 Topology data structure in OpenCascade
從上面的類圖可以看出只有三種拓樸對(duì)象有幾何表示數(shù)據(jù)：頂點(diǎn)（vertex）、邊（edge）、面（face），分別為BRep_TVertex、BRep_TEdge、BRep_TFace。
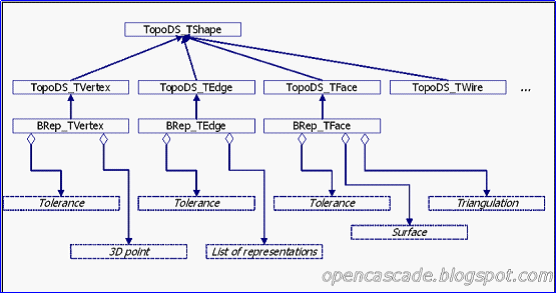
Figure 2.4 TopoDS_TShape class diagram
三、頂點(diǎn) Vertex
頂點(diǎn)（vertex）的位置用幾何點(diǎn)（gp_Pnt）來(lái)表示。點(diǎn)是幾何造型中的最基本元素，自由曲線、曲面或其他形體均可用有序的點(diǎn)集表示。用計(jì)算機(jī)存儲(chǔ)、管理、輸出形體的實(shí)質(zhì)就是對(duì)點(diǎn)集及其連接關(guān)系的處理。在正則形體定義中，不允許孤立點(diǎn)存在。
頂點(diǎn)的另一個(gè)重要屬性是容差（Tolerance），用來(lái)表示位置精度。頂點(diǎn)容差T的幾何意義為以頂點(diǎn)為圓心半徑為T的球。這個(gè)球必須包含所有與這個(gè)頂點(diǎn)相連的邊的曲線的端點(diǎn)。
Figure 3.1 Vertex Tolerance
與其他幾何庫(kù)有全局精度（global precision）不同，OpenCascade把容差作為局部屬性（local properties）。由圖2.4可知，容差是頂點(diǎn)、邊、面的屬性。這種方法有助于用更一般的方式來(lái)描述高精度的模型。如下圖所示：
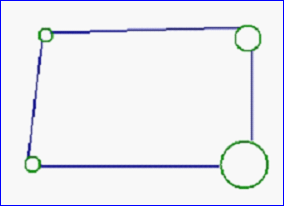
Figure 3.2 Vertex with different tolerance
如果從底層來(lái)創(chuàng)建形狀，最好的方法就是指定最小的允許誤差。默認(rèn)值Precision::Confusion()為1e-07。
下面討論頂點(diǎn)的朝向（orientation）屬性。它沒(méi)有直接的幾何意義，但是根據(jù)約定，若頂點(diǎn)的朝向?qū)傩灾禐門opAbs_FORWARD，它就必須與表示邊的曲線的參數(shù)值小的端部匹配。相應(yīng)地，TopAbs_REVERSED的頂點(diǎn)與參數(shù)值大的端部匹配。例如，有條邊位于圓弧上，圓弧半徑為1且在Z＝0的平面上，起點(diǎn)為（1，0，0），向－Z軸向，曲線為逆時(shí)針?lè)较颉Ｋ皂旤c(diǎn)（1，0，0）的朝向?yàn)門opAbs_FORWARD，頂點(diǎn)（0，1，0）的朝向?yàn)門opAbs_REVERSED。如下圖所示：
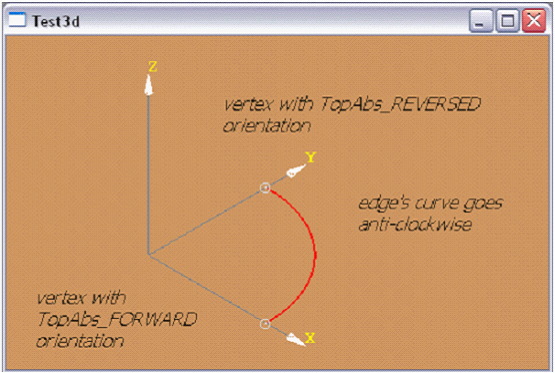
Figure 3.3 Vertex Orientation attribute
實(shí)現(xiàn)上圖所示的程序代碼如下所示：
1 /*
2 * Copyright (c) 2013 eryar All Rights Reserved.
3 *
4 * File : Main.cpp
5 * Author : eryar@163.com
6 * Date : 2013-08-17 21:46
7 * Version : 1.0v
8 *
9 * Description : Demonstrate how to build a edge bottom-up by BRepBuilderAPI_MakeEdge,
10 * and how to access vertex infomation by BRep_Tool.
11 *
12 */
13
14 // OpenCascade library.
15 #define WNT
16 #include <gp_Circ.hxx>
17 #include <GC_MakeArcOfCircle.hxx>
18
19 #include <TopoDS_Edge.hxx>
20 #include <BRep_Tool.hxx>
21 #include <BRepBuilderAPI_MakeEdge.hxx>
22 #include <BRepBuilderAPI_MakeVertex.hxx>
23
24 #pragma comment(lib, "TKernel.lib")
25 #pragma comment(lib, "TKMath.lib")
26 #pragma comment(lib, "TKBRep.lib")
27 #pragma comment(lib, "TKGeomBase.lib")
28 #pragma comment(lib, "TKTopAlgo.lib")
29
30 /**
31 * @breif Dump orientation types.
32 * Orientation definitaion:
33 * enum TopAbs_Orientation {
34
35 * TopAbs_FORWARD,
36
37 * TopAbs_REVERSED,
38
39 * TopAbs_INTERNAL,
40
41 * TopAbs_EXTERNAL
42
43 * };
44 */
45 std::string DumpOrientation(const TopAbs_Orientation& orient)
46 {
47 std::string strType;
48
49 switch (orient)
50 {
51 case TopAbs_FORWARD:
52 strType = "TopAbs_FORWARD";
53 break;
54
55 case TopAbs_REVERSED:
56 strType = "TopAbs_REVERSED";
57 break;
58
59 case TopAbs_INTERNAL:
60 strType = "TopAbs_INTERNAL";
61 break;
62
63 case TopAbs_EXTERNAL:
64 strType = "TopAbs_EXTERNAL";
65 break;
66 }
67
68 return strType;
69 }
70
71 /**
72 * @breif Dump attributes of the vertex.
73 */
74 void DumpVertex(const TopoDS_Vertex& v)
75 {
76 gp_Pnt p = BRep_Tool::Pnt(v);
77 Standard_Real dTolerance = BRep_Tool::Tolerance(v);
78
79 std::cout<<"Vertex position: ("<<p.X()<<", "<<p.Y()<<", "<<p.Z()<<")"<<std::endl;
80 std::cout<<"Vertex Tolerance: "<<dTolerance<<std::endl;
81 std::cout<<"Vertex orientation: "<<DumpOrientation(v.Orientation())<<std::endl;
82 std::cout<<std::endl;
83 }
84
85 int main(int argc, char* argv[])
86 {
87 gp_Circ circle;
88 TopoDS_Edge edge;
89 TopoDS_Vertex vertex1;
90 TopoDS_Vertex vertex2;
91 BRepBuilderAPI_MakeEdge edgeBuilder;
92
93 circle.SetRadius(1.0);
94 circle.SetAxis(gp::OZ());
95
96 edgeBuilder.Init(GC_MakeArcOfCircle(circle, 0.0, M_PI/2.0, Standard_True));
97
98 // Test single vertex.
99 /*vertex1 = BRepBuilderAPI_MakeVertex(gp_Pnt(100.0, 200.0, 300.0));
100 vertex2 = BRepBuilderAPI_MakeVertex(gp_Pnt(500.0, 600.0, 700.0));
101
102 std::cout<<"Single vetex test: "<<std::endl;
103
104 std::cout<<"Vertex 1 attributes: "<<std::endl;
105 DumpVertex(vertex1);
106
107 std::cout<<"Vertex 2 attributes: "<<std::endl;
108 DumpVertex(vertex2);*/
109
110 edge = edgeBuilder.Edge();
111 vertex1 = edgeBuilder.Vertex1();
112 vertex2 = edgeBuilder.Vertex2();
113
114 std::cout<<"Test vertex belong to edge:"<<std::endl;
115
116 std::cout<<"Vertex 1 attributes: "<<std::endl;
117 DumpVertex(vertex1);
118
119 std::cout<<"Vertex 2 attributes: "<<std::endl;
120 DumpVertex(vertex2);
121
122 return 0;
123 }
程序運(yùn)行結(jié)果如下圖所示：
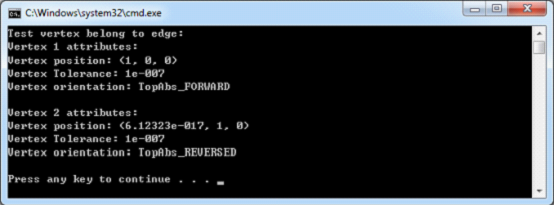
Figure 3.4 Code example result
BRep_Builder是從底層創(chuàng)建拓樸結(jié)構(gòu)的類。如下代碼所示為從底層創(chuàng)建頂點(diǎn)的示例：
1 gp_Pnt aPoint(100.0, 200.0, 300.0)
2
3 BRep_Builder aBuilder;
4
5 TopoDS_Vertex aVertex;
6
7 aBuilder.MakeVertex(aVertex, aPoint, Precision::Confusion());
8
9 aVertex.Orientation(TopAbs_REVERSED);
有一個(gè)方便的類也可用來(lái)創(chuàng)建頂點(diǎn)BRepBuilderAPI_MakeVertex，其內(nèi)部也是使用了類BRep_Builder。所以，若想從底層創(chuàng)建拓樸結(jié)構(gòu)，必須要熟悉BRep_Builder。
BRep_Tool是用來(lái)訪問(wèn)拓樸結(jié)構(gòu)中幾何信息的工具，他的大部分的函數(shù)是靜態(tài)的。如下代碼所示為獲取頂點(diǎn)的容差和幾何點(diǎn)的方法：
1 Standard_Real aTolerance = BRep_Tool::Tolerance(aVertex);
2
3 gp_Pnt aPoint = BRep_Tool::Pnt(aVertex);
4
四、BRep文件中Vertex的數(shù)據(jù)
結(jié)合《BRep Format Description White Paper》中對(duì)<vertex data>的描述，及程序代碼中對(duì)頂點(diǎn)數(shù)據(jù)的讀取，分析OpenCascade的BRep表示中的頂點(diǎn)。
Figure 4.1 NBF-like definition of Vertex
詳細(xì)說(shuō)明：
<vertex data representation u parameter>u的使用方法說(shuō)明如下：
<vertex data representation data 1> 和參數(shù)u定義了三維曲線C上的點(diǎn)V的位置。參數(shù)u是曲線C上點(diǎn)V對(duì)應(yīng)的參數(shù)：C（u）＝V。
<vertex data representation data 2>和參數(shù)u定義了曲面上的二維曲線C上點(diǎn)V的位置。參數(shù)u是曲線C上點(diǎn)V對(duì)應(yīng)的參數(shù)：C（u）＝V。
<vertex data representation data 3>和參數(shù)u及<vertex data representation v parameter>v定義了曲面S上的點(diǎn)V：S（u，v）＝V。
<vertex data tolerance>t定義如下所示：
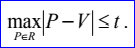
讀取Vertex部分的程序代碼摘抄如下：
1 //---------
2 // vertex
3 //---------
4
5 case TopAbs_VERTEX :
6 {
7 TopoDS_Vertex& V = TopoDS::Vertex(S);
8
9 // Read the point geometry
10 IS >> tol;
11 IS >> X >> Y >> Z;
12 myBuilder.MakeVertex(V,gp_Pnt(X,Y,Z),tol);
13 Handle(BRep_TVertex) TV = Handle(BRep_TVertex)::DownCast(V.TShape());
14
15 BRep_ListOfPointRepresentation& lpr = TV->ChangePoints();
16 TopLoc_Location L;
17
18 do {
19 IS >> p1 >> val;
20
21 Handle(BRep_PointRepresentation) PR;
22 switch (val) {
23
24 case 1 :
25 {
26 IS >> c;
27
28 // Modified by Sergey KHROMOV - Wed Apr 24 13:59:09 2002 Begin
29 if (myCurves.Curve(c).IsNull())
30 break;
31 // Modified by Sergey KHROMOV - Wed Apr 24 13:59:13 2002 End
32
33 Handle(BRep_PointOnCurve) POC =
34 new BRep_PointOnCurve(p1,
35 myCurves.Curve(c),
36 L);
37 PR = POC;
38 }
39 break;
40
41 case 2 :
42 {
43 IS >> pc >> s;
44
45 // Modified by Sergey KHROMOV - Wed Apr 24 13:59:09 2002 Begin
46 if (myCurves2d.Curve2d(pc).IsNull() ||
47 mySurfaces.Surface(s).IsNull())
48 break;
49 // Modified by Sergey KHROMOV - Wed Apr 24 13:59:13 2002 End
50
51 Handle(BRep_PointOnCurveOnSurface) POC =
52 new BRep_PointOnCurveOnSurface(p1,
53 myCurves2d.Curve2d(pc),
54 mySurfaces.Surface(s),
55 L);
56 PR = POC;
57 }
58 break;
59
60 case 3 :
61 {
62 IS >> p2 >> s;
63
64 // Modified by Sergey KHROMOV - Wed Apr 24 13:59:09 2002 Begin
65 if (mySurfaces.Surface(s).IsNull())
66 break;
67 // Modified by Sergey KHROMOV - Wed Apr 24 13:59:13 2002 End
68
69 Handle(BRep_PointOnSurface) POC =
70 new BRep_PointOnSurface(p1,p2,
71 mySurfaces.Surface(s),
72 L);
73 PR = POC;
74 }
75 break;
76 }
77
78 if (val > 0) {
79 IS >> l;
80 if (!PR.IsNull()) {
81 PR->Location(Locations().Location(l));
82 lpr.Append(PR);
83 }
84 }
85 } while (val > 0);
86 }
87 break;
從BRep文件中可知，大部分的Vertex只有如下數(shù)據(jù)：
1 0101101
2 *
3 Ve
4 1e-007
5 2 3 0
6 0 0
即只使用了BRep_Builder.MakeVertex()創(chuàng)建創(chuàng)建頂點(diǎn)（vertex），還可記錄頂點(diǎn)的類型：
1. 若頂點(diǎn)在三維空間中的曲線上Geom_Curve，則記錄三維曲線的索引號(hào)及參數(shù)u；
2. 若頂點(diǎn)在二維空間中的曲線上Geom2d_Curve，則記錄二維曲線的索引號(hào)及參數(shù)u；
3. 若頂點(diǎn)在曲面上Geom_Surface，則記錄曲面的索引號(hào)及參數(shù)（u，v）；
五、結(jié)論 Conclusion
結(jié)合博客“OpenCascade notes”及《BRep format Description white paper》對(duì)OpenCascade的拓樸結(jié)構(gòu)中的頂點(diǎn)（vertex）的屬性數(shù)據(jù)進(jìn)行說(shuō)明。結(jié)合程序說(shuō)明了頂點(diǎn)的容差及朝向的意義及從底層創(chuàng)建頂點(diǎn)的方法。通過(guò)BRep_Tool的靜態(tài)函數(shù)可以獲取頂點(diǎn)的幾何數(shù)據(jù)及其他屬性。
發(fā)現(xiàn)在BRep文件中還對(duì)頂點(diǎn)進(jìn)行了分類：三維曲線上的點(diǎn)、二維曲線上的點(diǎn)和曲面上的點(diǎn)。
六、參考資料
1. OpenCascade notes: opencascade.blogspot.com
2. 孫家廣等. 計(jì)算機(jī)圖形學(xué). 清華大學(xué)出版社