B樣條曲線比Bezier曲線更靈活，它的靈活性來自于你對基函數靈活地控制。我將對B樣條的各組成部分進行講解，首先講一下控制頂點（Control Points）。

Control Points 控制頂點

Bezier曲線的控制頂點對整條曲線都有影響，即改變某一頂點的位置，對整條曲線都有影響，因而Bezier曲線不具有局部修改性。

由于靈活性的緣故，你可以對B樣條設置任意數量的控制頂點，也可以確定各控制頂點的影響范圍。

Degree and Order 次數和階數

多項式曲線時，曲線的次數是由多項式中變量指數最高項確定。Bezier曲線時，曲線的次數由控制頂點數N確定，即N個控制頂點的曲線的次數是（N-1）次。基于這一點，我將引入一些新的術語來討論曲線的次數和階數，即階數（Order）由設計值k確定，次數（Degree）則為（k-1）。

B樣條把控制頂點數N與曲線的次數和控制頂點影響范圍解耦。再抽象點說，曲線上的點只受一些控制頂點的影響，而不是任意控制頂點。或者說每個控制頂點只影響曲線上的一部分點的值。這就有意思啦，因為你對曲線有了局部修改的權力。你可用16個控制頂點定義一條曲線，但是它的階數為4。如圖4.1所示，移動一個控制頂點只會影響曲線上的一部分。若要用Bezier曲線來實現，就只能是把幾個Bezier曲線拼接啦。

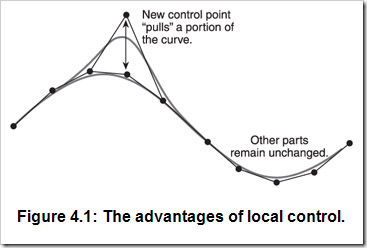
我已經講到了術語階數（Order）、次數（Degree），及控制頂點對曲線區間的影響，但是并沒有講到具體是怎樣影響的。使用Bezier曲線時，沒有任何的機制來限制影響的區間，因為任意一個控制頂點的改變都會影響到曲線上的每個點。B樣條給你更多的控制，正是由于有節點向量（Knot Vectors）的機制。

Knot Vectors 節點向量

節點向量的目的就是描述控制頂點的影響范圍。想象一下你想畫一個有五個控制頂點的三階曲線，每個控制頂點只會影響到參數區間上的曲線的一小部分。你可以描述任意一個控制頂點的影響范圍為：[t₀, t₃], [t ₁, t₄], [t₂, t₅], [t₃, t₆], [t₄, t₇]。也可以在一個單一序列中緊湊的寫成：[t₀ t₁ t₂ t₃ t₄ t₅ t₆ t₇]。這就是節點向量。圖4.3所示為正式地表示了節點向量的影響范圍：

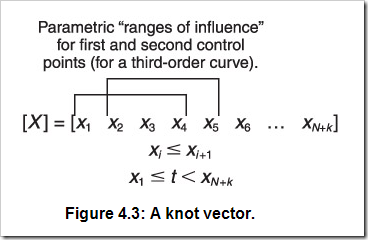
還可以從本例中推出幾個更普遍的結論。首先，一個節點向量必須有N+k個元素；其次，節點向量必須是單調遞增的。即每個節點向量的元素必須比前一個大或相等。單調遞增的區間可以是任意的，當然也可以是[0，1]。下面是三個節點向量的例子。注意第二個節點向量和第三個在功能上相同，即用它們將會生成相同的曲線：

[X] = [3 4 5 6 7 8]

[X] = [1 2 3 4 5 6 7 8]

[X] = [0.125 0.25 0.375 0.5 0.625 0.75 0.875 1.0]

本書中大部分情況下將會使用整型的節點向量值，如第二種，因為這樣解釋起來要簡單些。而在程序代碼中，我將使用單位化后的節點向量，因為當參數區間為[0，1]時，考慮不同的范圍要簡單些。這兩種情況產生的曲線沒什么不同。

通常喜歡按節點向量是否均勻分布把節點向量分為均勻節點向量和非均勻節點向量。各舉例如下：

• [X] = [1 2 3 4 5 6] (uniform)

• [X] = [1 3 5 7 9 11] (uniform)

• [X] = [1 2 2 3 3 4] (nonuniform)

• [X] = [1 2 3 3 4 5] (nonuniform)

節點向量還有兩種類型：開放（Open）和周期性的（Periodic）。

至此為止，你已經知道創建B樣條曲線的所有內容，除了B樣條的基函數。知道一系列控制頂點可以用來定義曲線；知道可以用階數及其相應的次數來描述曲線的屬性；知道節點向量的機制，控制頂點是怎樣來影響曲線的。你還需要一個基本的部分，即把上面所有組合在一起來畫些東西，這就是基函數（the Basis Function）。

B樣條基函數 B-Spline Basis Functions

在第三章講Bezier曲線時，生活要簡單的多。Bezier曲線的Bernstein基函數只是控制頂點的函數。現在，有了更多的靈活性，但是需要關注的就更多。（能力越大，責任越大。）除了控制頂點以外，B樣條基函數還需要解釋曲線的次數，還有由節點矢量定義的區間。這個基函數不是由Bernstein多項式定義的，而是由Cox-de Boor遞歸公式定義的。這個著名的遞推公式的發現是B樣條理論的最重要的進展。

B樣條基的性質：

1. 遞推性。由遞推公式可以表明；
2. 局部支承性。局部支承性表明B樣條基是定義在整個參數軸上，但僅在支承區間上有大于零的值，在這個區間外均為零。B樣條由其支承區間內的所有節點決定。
3. 規范性。

    

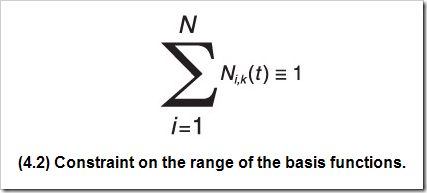
4. 可微性。在節點區間內部是無限次可微的。

這些公式初看起來很嚇人，其實不然，只要你理解它們都是做什么用的。畫Bezier曲線時，可以根據Bernstein基函數很容易就推出一個基函數。現在必須根據階數來遞推去找到基函數。從一階基函數開始推導，因為便于圖示和舉例。

想像一下我想用四個控制頂點畫一個四階三次曲線，我選擇節點矢量為[X] = [0, 0, 0, 0, 1, 1, 1, 1]。在繼續后面內容之前，用圖4.3中的術語來考慮一下這個節點矢量。這個節點矢量讓每個控制頂點的改變都會影響到整條曲線，聽起來很耳熟？