跟國內大多數計算機輔助幾何造型或計算幾何的教材不同,《Focus on Curves and Surfaces》介紹Bezier的方法簡單,讓人易于接受。現將本節內容翻譯如下,若有錯誤,請指出。國內教材上來就是給出定義,而她是按幾何方法推導出了二次Bezier曲線的伯恩斯坦(Bernstein)基函數,讓人豁然開朗。
==================================================================================================================================================
Bezier曲線的參數方程定義 Bezier Curves Defined in Parametric Terms
原來的CAD/CAM工具和高精度的機器設備、工程師和繪圖師繪制的曲線非常粗糙,精度不高。典型地,他們先標記出曲線上很少的幾個點,再使用一個曲線板或其它類似的工具畫出一條通過這些點的最佳配合的曲線。當引入計算機輔助制造技術后,這種方法就不能接受啦,因為自動化的設備可以制造出高精度的零件。Pierre Bezier在1960年代法國雷諾汽車公司工作時也遇到了這個問題。他發明了Bezier曲線作為高精度擬合曲線的一種方法。計算機驅動的機床設備可以精確地、可靠地的制造出曲線。和其它偉大的發明一樣,其他的發明家也同時做出了成績,但是這種擬合曲線的方法還是以Bezier的名字命名。
注:在第四章,B樣條曲線,你將會學到Bezier曲線可以認為是B樣條曲線的一個特例。本章中我將用嚴格的術語來解釋,為了后面更通用的B樣條曲線。
一些推導Bezier曲線的數學概念超出了本書的范圍,對于應用的人來說也不是很重要,所以我將用基本的幾何術語來描述這個公式。我已經講過了直線的參數方程,現在將把這些概念擴展到曲線。要畫一個線性曲線,至少需要三個點。這三個點叫做控制頂點(Control Points),把控制頂點連接起來就形成了特征多邊形(Control Polygon)。圖3.2所示為由三個控制頂點形成的二次曲線。
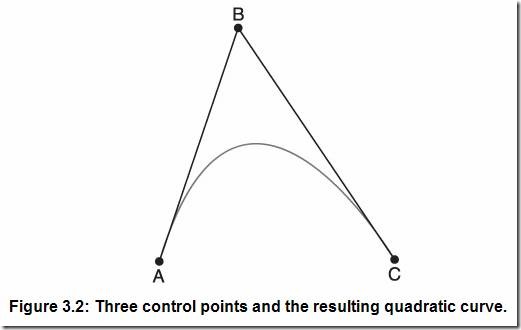
在我講述怎樣用參數方程的方法創建曲線之前,先考慮一個很簡單的幾何方法。圖3.2中的曲線可以用一個基本的細分方法來創建。對每個直線段,選中其中點,并將其相連,重復直到直線段太短而不能再細分時就創建出了光滑的曲線。圖3.3所示為使用這種方法的幾個步驟:
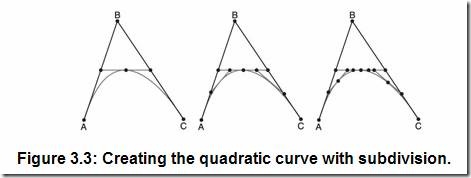
若你只是畫曲線,幾何方法完全夠用啦。在實際應用中,你很快就會發現這種方法的局限性。如果其中任意一點改變了,你必須重復所有的細分步驟只為了計算出一個點。顯然地,你需要一個方法來描述曲線上任意一點,這個方法就是通過控制頂點的方程來實現。這樣你只需要計算控制頂點的方程來求出曲線上的點而不需要再用細分方法啦。這聽起來你像是參數方程的活!
圖3.4與圖3.2有著相同的控制頂點,唯一的不同就是通過直線的參數方程來定義點。
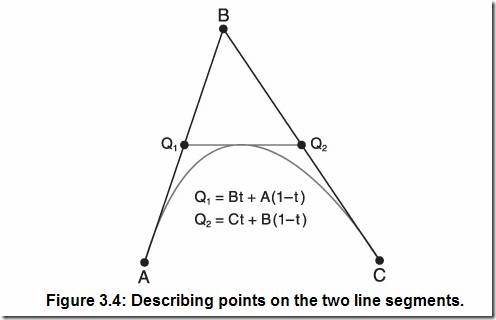
現在連接Q1和Q2。圖3.5所示為點Q3的參數方程與Q1和Q2的關系。
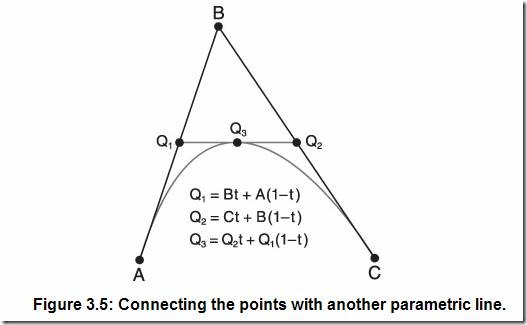
所以對于參數t的任意值,都可以在每條線段上找到一個與之對應的點,把它們連接上,就找到連接生成的新的直線上的一個點。圖3.5中的Q3即是如此。Q3的位置是由參數t和Q1、Q2的方程確定的,即是由A、B、C和t確定。把Q1、Q2的方程代入Q3的方程可以推導出Q3關于控制頂點和參數t的方程。推導過程如下:
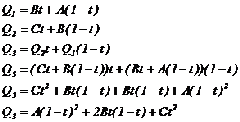
方程的最終形式將推導出相同的二次曲線,如圖3.2 和3.3。也是二次Bezier曲線的方程。也可以將其看作一系列基函數和相應的控制頂點和乘積。如下方程所示:
由基函數表示的Bezier曲線上的點: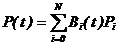
這個基函數就是伯恩斯坦基函數(Bernstein polynomials)。它確定對于任意參數值t,每個控制頂點對曲線的影響。Bezier曲線的控制頂點數也是不定的。對于控制頂點數量確定的伯恩斯坦基函數,可由如下方程求出:
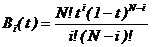
使用更多的控制頂點的缺點就是計算量會隨著控制頂點數的增加而增加。所以通常人們會限制控制頂點數為三或四。在三章剩余部分都以四個控制頂點為例,即三次Bezier曲線。其基函數可以上述方程求出,但為了簡單其見,列出如下:
三次Bezier曲線的四個基函數: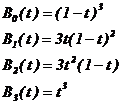
在三章或其它章節中畫出基函數有時是很有用的。圖3.6所示為四個基函數的圖形。參數t的區間是[0,1],函數值的區間也是[0,1]。
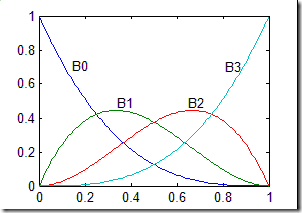
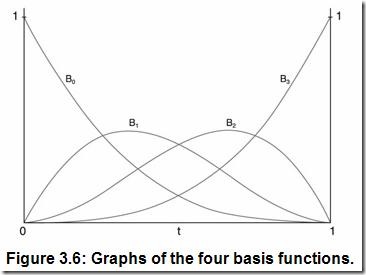
圖3.6揭示了Bezier曲線的基函數的幾個特性。首先:權性。即所有基函數的和在參數t取任意值時都為1。其次,端點性質。即曲線的端點通過特征多邊形的首末點。
圖3.6也揭示了Bezier曲線的一些局限性。每個控制頂點都會影響曲線上的點,端點除外。這就意味著在計算曲線上的點時需要計算很多控制頂點。結果就是控制頂點的個數決定了曲線的次數。曲線的次數是控制頂點數減1。改變任意一個控制頂點都會影響到曲線上的點,所以這就是沒有局部控制的作用。這也是Bezier的不足之處,在你確定曲線最終形狀時有點不夠靈活。由于這個原因,人們通常會把幾個三次Bezier曲線拼接,而不是用很多控制頂點來形成曲線。