91精品国产高清久久久久久国产嫩草 ,99精品国产99久久久久久97,四虎国产精品成人免费久久

Bézier Curve

Posted on 2011-11-20 15:18 eryar 閱讀(4462) 評論(0) 編輯收藏引用所屬分類: 2.OpenCASCADE

在產品零件設計中，許多自由曲面是通過自由曲線來構造的。對于自由曲線的設計，設計人員經常需要大致勾畫出曲線的形狀，用戶希望有一種方法能不再采用一般的代數描述，而采用直觀的具有明顯幾何意義的操作，使得設計的曲線能夠逼近曲線的形狀。采用插值方法，用戶設計的曲線形狀不但受曲線上型值點的約束，而且受到邊界條件影響，用戶不能靈活調整曲線形狀。但在產品設計中，曲線的設計是經過多次修改和調整來完成的，已有的方法完成這樣的功能并不容易。Bézier方法的出現改善了上述設計方法的不足，使用戶能方便地實現曲線形狀的修改。

一、Bézier曲線定義

1. 定義：用基函數表示的Bézier曲線為

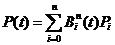
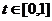
Bernstein基函數：

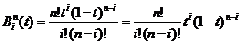
當N=3時，即特征多邊形有四個頂點，由上式可得到三次Bernstein基函數：

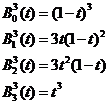
因此根據定義可把三次Bézier曲線表示為：

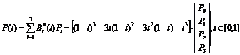
也可根據上式寫成矩陣形式，有點類似二次型：

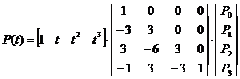
由上可知，只要給定特征多邊形的四個頂點矢量P₀P₁P₂P₃，并得用上式即可構造一條三次Bézier曲線。只要改變t值即可計算曲線上的點。對于曲線設計來說，采用這種特征多邊形頂點的方法比較方便、直觀。

二、編程實現

利用OpenGL的glut庫根據Bézier曲線定義來實現曲線的繪制，源程序如下：

// Bezier Curve Program

#include <gl\glut.h>

#define POINTS_NUM	100

// point structure
typedef struct SPoint{
	float	x;
	float	y;
}Point;

Point	ctrlPoint[4];

void	Initialize(void);
void	DrawScene(void);
void	myReshape(GLsizei w, GLsizei h);
void	PlotBezierCurveDirectly(void);
Point	PointOnBezierCurve(int i, int k, float t);
void	PlotBezierCurve(void);

void main(int argc, char* argv[]) {
	glutInit(&argc, argv);				// Initialize GLUT
	glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB);	// Set display mode
	glutInitWindowPosition(50,100);			// Set top-left display window position
	glutInitWindowSize(400, 300);			// set display window width and height
	glutCreateWindow("Bézier Curve");		 // Create display window

	Initialize();					// Execute initialization procedure
	glutDisplayFunc(DrawScene);			// Send graphics to display window
	glutReshapeFunc(myReshape);			// 

	glutMainLoop();					// Display everything and wait
}

/*
*/
void	Initialize(void) {
	//glClearColor(1.0, 1.0, 1.0, 0.0);		// Set Display-window color to white
	glMatrixMode(GL_PROJECTION);			// Set projection parameters
	glLoadIdentity();
	gluOrtho2D(0.0, 200, 0.0, 150);			// 

} // Initialize

/*
*/
void	myReshape(GLsizei w, GLsizei h) {
	// Reset viewport and projection parameter
	glViewport(0, 0, w, h);
	glMatrixMode(GL_PROJECTION);
	glLoadIdentity();
	gluOrtho2D(0, w, 0, h);
	glMatrixMode(GL_MODELVIEW);
} // myReshape

/*
*/
void	DrawScene(void) {
	glClear(GL_COLOR_BUFFER_BIT);			// Clear display window

	PlotBezierCurveDirectly();

	PlotBezierCurve();

	glFlush();					// Process all OpenGL routines as quickly possible
} // DrawScene


/*
	plot the Bezier Curve according to Definition.
*/
void	PlotBezierCurveDirectly(void) {
	// Basis functions
	#define B0(t)	((1.0 - t) * (1.0 - t) * (1.0 - t))
	#define B1(t)	(3.0 * t * (1.0 - t) * (1.0 - t))
	#define B2(t)	(3.0 * t * t * (1.0 - t))
	#define B3(t)	(t * t * t)

	// initialize control points
	Point	controlPoint[4];
	Point	plotPoint[POINTS_NUM];

	controlPoint[0].x	=	100.0;
	controlPoint[0].y	=	100.0;
	controlPoint[1].x	=	300.0;
	controlPoint[1].y	=	200.0;
	controlPoint[2].x	=	400.0;
	controlPoint[2].y	=	200.0;
	controlPoint[3].x	=	600.0;
	controlPoint[3].y	=	100.0;

	// calculate the points on the Bezier curve
	glColor3f(1.0, 0.0, 0.0f);			// set line segment geometry color to red
	glBegin(GL_LINE_STRIP);
	for (int i = 0; i < POINTS_NUM; ++i) {
		float	t	=	1.0 * i / POINTS_NUM;

		plotPoint[i].x	=	(B0(t) * controlPoint[0].x) +
					(B1(t) * controlPoint[1].x) +
					(B2(t) * controlPoint[2].x) +
					(B3(t) * controlPoint[3].x);

		plotPoint[i].y	=	(B0(t) * controlPoint[0].y) +
					(B1(t) * controlPoint[1].y) +
					(B2(t) * controlPoint[2].y) +
					(B3(t) * controlPoint[3].y);

		glVertex2f(plotPoint[i].x, plotPoint[i].y);
	}
	glEnd();

	// draw control points
	glColor3f(1.0, 1.0, 0.0f);
	glPointSize(6.0);
	glBegin(GL_POINTS);
		glVertex2f(controlPoint[0].x, controlPoint[0].y);
		glVertex2f(controlPoint[1].x, controlPoint[1].y);
		glVertex2f(controlPoint[2].x, controlPoint[2].y);
		glVertex2f(controlPoint[3].x, controlPoint[3].y);
	glEnd();

	// draw control polygon
	glColor3f(1.0, 0.0, 1.0f);
	glBegin(GL_LINE_STRIP);
		glVertex2f(controlPoint[0].x, controlPoint[0].y);
		glVertex2f(controlPoint[1].x, controlPoint[1].y);
		glVertex2f(controlPoint[2].x, controlPoint[2].y);
		glVertex2f(controlPoint[3].x, controlPoint[3].y);
	glEnd();

} // PlotBezierCurveDirectly

/*
*/
Point	PointOnBezierCurve(int i, int k, float t) {
	if (k == 0) {
		return ctrlPoint[i];
	}
	else {
		Point	point;
		Point	iPrev	=	PointOnBezierCurve(i, k-1, t);
		Point	iNext	=	PointOnBezierCurve(i+1, k-1, t);

		point.x	=	(1.0 - t) * iPrev.x + t * iNext.x;
		point.y	=	(1.0 - t) * iPrev.y + t * iNext.y;

		return point;
	}
} // PointOnBezierCurve

/*
	Use recursive algorithm to plot Bezier Curve.
*/
void	PlotBezierCurve(void) {

	// initialize control points
	ctrlPoint[0].x	=	100.0;
	ctrlPoint[0].y	=	200.0;
	ctrlPoint[1].x	=	300.0;
	ctrlPoint[1].y	=	300.0;
	ctrlPoint[2].x	=	400.0;
	ctrlPoint[2].y	=	500.0;
	ctrlPoint[3].x	=	600.0;
	ctrlPoint[3].y	=	300.0;

	Point	plotPoint[POINTS_NUM];

	// calculate the points on the Bezier curve
	glColor3f(1.0, 0.0, 0.0f);			// set line segment geometry color to red
	glBegin(GL_LINE_STRIP);
	for (int i = 0; i < POINTS_NUM; ++i) {
		float	t	=	1.0 * i / POINTS_NUM;

		plotPoint[i]	=	PointOnBezierCurve(0,3,t);
		
		glVertex2f(plotPoint[i].x, plotPoint[i].y);
	}
	glEnd();

	// draw control points
	glColor3f(1.0, 1.0, 1.0f);
	glPointSize(6.0);
	glBegin(GL_POINTS);
		glVertex2f(ctrlPoint[0].x, ctrlPoint[0].y);
		glVertex2f(ctrlPoint[1].x, ctrlPoint[1].y);
		glVertex2f(ctrlPoint[2].x, ctrlPoint[2].y);
		glVertex2f(ctrlPoint[3].x, ctrlPoint[3].y);
	glEnd();

	// draw control polygon
	glColor3f(0.0, 0.0, 1.0f);
	glBegin(GL_LINE_STRIP);
		glVertex2f(ctrlPoint[0].x, ctrlPoint[0].y);
		glVertex2f(ctrlPoint[1].x, ctrlPoint[1].y);
		glVertex2f(ctrlPoint[2].x, ctrlPoint[2].y);
		glVertex2f(ctrlPoint[3].x, ctrlPoint[3].y);
	glEnd();

} // PlotBezierCurve

程序運行結果如圖1所示：

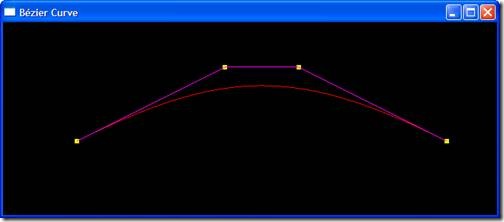
圖1 根據定義實現的Bézier曲線

可修改特征多邊形頂點變量controlPoint來看看相應的Bézier曲線的變化。

三、Bézier曲線的遞推算法

計算Bézier曲線上的點，可用Bézier曲線方程直接計算，但使用de Casteljau提出的遞推算法則要簡單得多。

Bézier曲線的Bernstein基函數的遞推性質

由于組合數的遞推性：

因此有

為了保證公式可計算，我們約定：在以上公式中，凡當指標超出范圍，以至記號不具有意義時，都應理解為零，如：

根據Bézier曲線定義可知：

這說明一條n次Bézier曲線可表示為分別由前后n個控制頂點決定的兩條n-1次Bézier曲線的線性組合。由此可得Bézier曲線上某一點遞歸求值的de Casteljau算法：

其中：

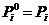——，是定義Bézier曲線的控制點；

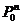——，即是曲線P(t)上具有參數t的點；

用這一遞推公式在給定參數下，求Bézier曲線上一點P(t)非常有效。de Casteljau算法穩定可靠，直觀簡便，可以編寫出十分簡捷的程序，是計算Bézier曲線的基本算法和標準算法。

四、de Casteljau算法的程序實現

根據遞推公式可寫出Bézier曲線的遞歸算法，如下：

/*
*/
Point    PointOnBezierCurve(int i, int k, float t) {
    if (k == 0) {
        return ctrlPoint[i];
    }
    else {
        Point    point;
        Point    iPrev    =    PointOnBezierCurve(i, k-1, t);
        Point    iNext    =    PointOnBezierCurve(i+1, k-1, t);

        point.x    =    (1.0 - t) * iPrev.x + t * iNext.x;
        point.y    =    (1.0 - t) * iPrev.y + t * iNext.y;

        return point;
    }
} // PointOnBezierCurve

.csharpcode, .csharpcode pre { font-size: small; color: black; font-family: consolas, "Courier New", courier, monospace; background-color: #ffffff; /*white-space: pre;*/ } .csharpcode pre { margin: 0em; } .csharpcode .rem { color: #008000; } .csharpcode .kwrd { color: #0000ff; } .csharpcode .str { color: #006080; } .csharpcode .op { color: #0000c0; } .csharpcode .preproc { color: #cc6633; } .csharpcode .asp { background-color: #ffff00; } .csharpcode .html { color: #800000; } .csharpcode .attr { color: #ff0000; } .csharpcode .alt { background-color: #f4f4f4; width: 100%; margin: 0em; } .csharpcode .lnum { color: #606060; }

其中，為了保存數據的方便，控制頂點數組變量ctrlPoint為全局變量。

根據遞推算法實現Bézier曲線與根據定義實現的程序效果如下圖2所示：

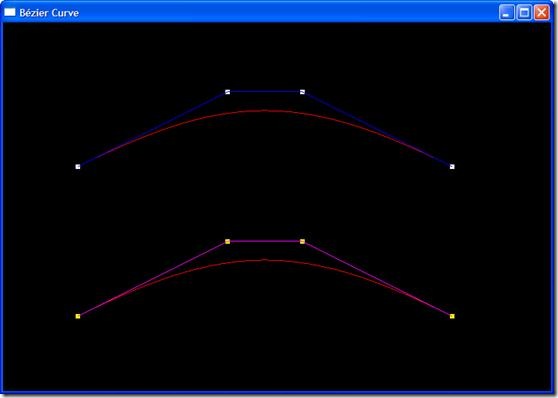
圖2 圖中上面部分為用遞推算法實現，下面部分為用定義實現。

源程序如下：

// Bezier Curve Program

// File : BezierCurve.cpp

#include <gl\glut.h>

#define POINTS_NUM 100

// point structure

typedef struct SPoint{

float x;

float y;

}Point;

Point ctrlPoint[4]; // control point for recursive algorithm Bezier Curve

void Initialize(void);

void DrawScene(void);

void myReshape(GLsizei w, GLsizei h);

void PlotBezierCurveDirectly(void);

Point PointOnBezierCurve(int i, int k, float t);

void PlotBezierCurve(void);

void main(int argc, char* argv[]) {

glutInit(&argc, argv); // Initialize GLUT

glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB); // Set display mode

glutInitWindowPosition(50,100); // Set top-left display window position

glutInitWindowSize(400, 300); // set display window width and height

glutCreateWindow("Bézier Curve"); // Create display window

Initialize(); // Execute initialization procedure

glutDisplayFunc(DrawScene); // Send graphics to display window

glutReshapeFunc(myReshape); //

glutMainLoop(); // Display everything and wait

}

void Initialize(void) {

//glClearColor(1.0, 1.0, 1.0, 0.0); // Set Display-window color to white

glMatrixMode(GL_PROJECTION); // Set projection parameters

glLoadIdentity();

gluOrtho2D(0.0, 200, 0.0, 150); //

} // Initialize

void myReshape(GLsizei w, GLsizei h) {

// Reset viewport and projection parameter

glViewport(0, 0, w, h);

glMatrixMode(GL_PROJECTION);

glLoadIdentity();

gluOrtho2D(0, w, 0, h);

glMatrixMode(GL_MODELVIEW);

} // myReshape

void DrawScene(void) {

glClear(GL_COLOR_BUFFER_BIT); // Clear display window

PlotBezierCurveDirectly();

PlotBezierCurve();

glFlush(); // Process all OpenGL routines as quickly possible

} // DrawScene

plot the Bezier Curve according to Definition.

void PlotBezierCurveDirectly(void) {

// Basis functions

#define B0(t) ((1.0 - t) * (1.0 - t) * (1.0 - t))

#define B1(t) (3.0 * t * (1.0 - t) * (1.0 - t))

#define B2(t) (3.0 * t * t * (1.0 - t))

#define B3(t) (t * t * t)

// initialize control points

Point controlPoint[4];

Point plotPoint[POINTS_NUM];

controlPoint[0].x = 100.0;

controlPoint[0].y = 100.0;

controlPoint[1].x = 300.0;

controlPoint[1].y = 200.0;

controlPoint[2].x = 400.0;

controlPoint[2].y = 200.0;

controlPoint[3].x = 600.0;

controlPoint[3].y = 100.0;

// calculate the points on the Bezier curve

glColor3f(1.0, 0.0, 0.0f); // set line segment geometry color to red

glBegin(GL_LINE_STRIP);

for (int i = 0; i < POINTS_NUM; ++i) {

float t = 1.0 * i / POINTS_NUM;

plotPoint[i].x = (B0(t) * controlPoint[0].x) +

(B1(t) * controlPoint[1].x) +

(B2(t) * controlPoint[2].x) +

(B3(t) * controlPoint[3].x);

plotPoint[i].y = (B0(t) * controlPoint[0].y) +

(B1(t) * controlPoint[1].y) +

(B2(t) * controlPoint[2].y) +

(B3(t) * controlPoint[3].y);

glVertex2f(plotPoint[i].x, plotPoint[i].y);

}

glEnd();

// draw control points

glColor3f(1.0, 1.0, 0.0f);

glPointSize(6.0);

glBegin(GL_POINTS);

glVertex2f(controlPoint[0].x, controlPoint[0].y);

glVertex2f(controlPoint[1].x, controlPoint[1].y);

glVertex2f(controlPoint[2].x, controlPoint[2].y);

glVertex2f(controlPoint[3].x, controlPoint[3].y);

glEnd();

// draw control polygon

glColor3f(1.0, 0.0, 1.0f);

glBegin(GL_LINE_STRIP);

glVertex2f(controlPoint[0].x, controlPoint[0].y);

glVertex2f(controlPoint[1].x, controlPoint[1].y);

glVertex2f(controlPoint[2].x, controlPoint[2].y);

glVertex2f(controlPoint[3].x, controlPoint[3].y);

glEnd();

} // PlotBezierCurveDirectly

Point PointOnBezierCurve(int i, int k, float t) {

if (k == 0) {

return ctrlPoint[i];

}

else {

Point point;

Point iPrev = PointOnBezierCurve(i, k-1, t);

Point iNext = PointOnBezierCurve(i+1, k-1, t);

point.x = (1.0 - t) * iPrev.x + t * iNext.x;

point.y = (1.0 - t) * iPrev.y + t * iNext.y;

return point;

}

} // PointOnBezierCurve

Use recursive algorithm to plot Bezier Curve.

void PlotBezierCurve(void) {

// initialize control points

ctrlPoint[0].x = 100.0;

ctrlPoint[0].y = 300.0;

ctrlPoint[1].x = 300.0;

ctrlPoint[1].y = 400.0;

ctrlPoint[2].x = 400.0;

ctrlPoint[2].y = 400.0;

ctrlPoint[3].x = 600.0;

ctrlPoint[3].y = 300.0;

Point plotPoint[POINTS_NUM];

// calculate the points on the Bezier curve

glColor3f(1.0, 0.0, 0.0f); // set line segment geometry color to red

glBegin(GL_LINE_STRIP);

for (int i = 0; i < POINTS_NUM; ++i) {

float t = 1.0 * i / POINTS_NUM;

plotPoint[i] = PointOnBezierCurve(0,3,t);

glVertex2f(plotPoint[i].x, plotPoint[i].y);

}

glEnd();

// draw control points

glColor3f(1.0, 1.0, 1.0f);

glPointSize(6.0);

glBegin(GL_POINTS);

glVertex2f(ctrlPoint[0].x, ctrlPoint[0].y);

glVertex2f(ctrlPoint[1].x, ctrlPoint[1].y);

glVertex2f(ctrlPoint[2].x, ctrlPoint[2].y);

glVertex2f(ctrlPoint[3].x, ctrlPoint[3].y);

glEnd();

// draw control polygon

glColor3f(0.0, 0.0, 1.0f);

glBegin(GL_LINE_STRIP);

glVertex2f(ctrlPoint[0].x, ctrlPoint[0].y);

glVertex2f(ctrlPoint[1].x, ctrlPoint[1].y);

glVertex2f(ctrlPoint[2].x, ctrlPoint[2].y);

glVertex2f(ctrlPoint[3].x, ctrlPoint[3].y);

glEnd();

} // PlotBezierCurve

因此，根據遞歸算法繪制Bézier曲線的程序簡單直觀，便于把數學公式與程序對應。

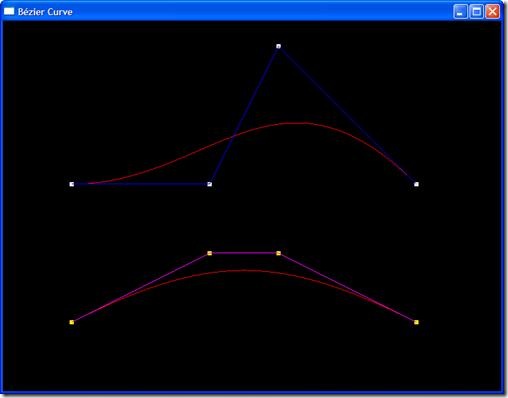
圖3 修改控制頂點后效果圖

只有注冊用戶登錄后才能發表評論。
【推薦】100%開源！大型工業跨平臺軟件C++源碼提供，建模，組態！

相關文章: OpenCASCADE HLR 輪廓線 OpenCASCADE-HLR Edge OpenCASCADE 線面求交 OpenCASCADE二維曲線求交 OpenCASCADE曲線上點的反求 OpenCASCADE - 曲線自交 OpenCASCADE 曲線求交 [書]-OpenCASCADE參考書籍 OpenCASCADE 掃掠曲面布爾數據面的相交

網站導航: 博客園 IT新聞 BlogJava 博問 Chat2DB 管理

eryar

導航

公告

常用鏈接

留言簿(107)

隨筆分類(692)

隨筆檔案(603)

Links

搜索

最新評論

閱讀排行榜

評論排行榜

Bézier Curve