Android 上實現水波特效
羅朝輝(http://www.shnenglu.com/kesalin)
轉載請注明出處
說明:
本文算法部分整理自 GameRes
上的資料,原作者 Imagic。我只是在學習 Android 的過程中,想到這個特效,然后就在Android 上實現出來,并在源算法的基礎上添加了雨滴滴落特效,以及劃過水面時的漣漪特效。 該程序在模擬器和真機上運行速度都較慢,需要進一步優化或使用 JNI 實現,如果你想到好的優化算法,請聯系我:kesalin@gmail.com。
示例程序下載:http://www.shnenglu.com/Files/kesalin/RippleDemo.zip
基礎知識:
在講解代碼之前,我們來回顧一下在高中的物理課上我們所學的關于水波的知識。水波有擴散,衰減,折射,反射,衍射等幾個特性:
擴散:當你投一塊石頭到水中,你會看到一個以石頭入水點為圓心所形成的一圈圈的水波,這里,你可能會被這個現象所誤導,以為水波上的每一點都是以石頭入水點為中心向外擴散的,這是錯誤的。實際上,水波上的任何一點在任何時候都是以自己為圓心向四周擴散的,之所以會形成一個環狀的水波,是因為水波的內部因為擴散的對稱而相互抵消了。
衰減:因為水是有阻尼的,否則,當你在水池中投入石頭,水波就會永不停止的震蕩下去。
折射:因為水波上不同地點的傾斜角度不同,所以我們從觀察點垂直往下看到的水底并不是在觀察點的正下方,而有一定的偏移。如果不考慮水面上部的光線反射,這就是我們能感覺到水波形狀的原因。
反射:水波遇到障礙物會反射。
衍射:在水池中央放上一塊礁石,或放一個中間有縫的隔板,那么就能看到水波的衍射現象了。
算法推導:
好了,有了這幾個特性,再運用數學和幾何知識,我們就可以模擬出真實的水波了。但是,如果你曾用3DMax做過水波的動畫,你就會知道要渲染出一幅真實形狀的水波畫面少說也得好幾十秒,而我們現在需要的是實時的渲染,每秒種至少也得渲染20幀才能使得水波得以平滑的顯示。考慮到電腦運算的速度,我們不可能按照正弦函數或精確的公式來構造水波,不能用乘除法,更不能用sin、cos等三角函數,只能用一種取近似值的快速算法,盡管這種算法存在一定誤差,但是為了滿足實時動畫的要求,我們不得不這樣做。
首先我們要建立兩個與水池圖象一樣大小的數組buf1[PoolWidth * PoolHeight]和buf2[PoolWidth * PoolHeight](PoolWidth 為水池圖象的象素寬度、PoolHeight 為水池圖象的象素高度),用來保存水面上每一個點的前一時刻和后一時刻波幅數據,因為波幅也就代表了波的能量,所以在后面我們稱這兩個數組為波能緩沖區。水面在初始狀態時是一個平面,各點的波幅都為0,所以,這兩個數組的初始值都等于0。
下面來推導計算波幅的公式
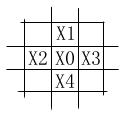
我們假設存在這樣一個一次公式,可以在任意時刻根據某一個點周圍前、后、左、右四個點以及該點自身的振幅來推算出下一時刻該點的振幅,那么,我們就有可能用歸納法求出任意時刻這個水面上任意一點的振幅。如左圖,你可以看到,某一時刻,X0點的振幅除了受X0點自身振幅的影響外,同時受來自它周圍前、后、左、右四個點(X1、X2、X3、X4)的影響(為了簡化,我們忽略了其它所有點),而且,這四個點對X0點的影響力可以說是機會均等的。那么我們可以假設這個一次公式為:
|
X0’
= a * (X1 + X2 + X3 + X4) + b * X0
(公式1)
|
a, b為待定系數,X0’ 為X0點下一時刻的振幅,
X0、X1、X2、X3、X4為當前時刻的振幅
下面我們來求解a和b。
假設水的阻尼為0。在這種理想條件下,水的總勢能將保持不變,水波永遠波動。也就是說在任何時刻,所有點的振幅的和保持不變。那么可以得到下面這個公式:
|
X0’ + X1’ + ... + Xn’ = X0 + X1 + ... + Xn
|
將每一個點用公式1替代,代入上式,得到:
|
(4a + b) * X0 + (4a + b) * X1 + ... (4a + b) * Xn = X0 + X1 + ... + Xn =>
4a + b = 1
|
找出一個最簡解:a = 1/2、b = -1。
因為1/2可以用移位運算符 “>>”
來進行,不用進行乘除法,所以,這組解是最適用的而且是最快的。那么最后得到的公式就是:
|
X0’=(X1 + X2 + X3 + X4)/ 2 - X0
|
好了,有了上面這個近似公式,你就可以推廣到下面這個一般結論:已知某一時刻水面上任意一點的波幅,那么,在下一時刻,任意一點的波幅就等于與該點緊鄰的前、后、左、右四點的波幅的和除以2、再減去該點的波幅。
應該注意到,水在實際中是存在阻尼的,否則,用上面這個公式,一旦你在水中增加一個波源,水面將永不停止的震蕩下去。所以,還需要對波幅數據進行衰減處理,讓每一個點在經過一次計算后,波幅都比理想值按一定的比例降低。這個衰減率經過測試,用1/32比較合適,也就是1/2^5。可以通過移位運算很快的獲得。
到這里,水波特效算法中最艱難的部分已經明了,下面是Android 源程序中計算波幅數據的代碼。
|
// 某點下一時刻的波幅算法為:上下左右四點的波幅和的一半減去當前波幅,即
// X0' =(X1 + X2 + X3 + X4)/ 2 - X0
// +----x3----+
// + | +
// + | +
// x1---x0----x2
// + | +
// + | +
// +----x4----+
//
void rippleSpread()
{
int pixels = m_width * (m_height - 1);
for (int i = m_width; i < pixels; ++i) {
// 波能擴散:上下左右四點的波幅和的一半減去當前波幅
// X0' =(X1 + X2 + X3 + X4)/ 2 - X0
//
m_buf2[i] =
(short)(((m_buf1[i - 1] + m_buf1[i + 1]+
m_buf1[i - m_width] + m_buf1[i + m_width]) >> 1)
- m_buf2[i]);
// 波能衰減 1/32
//
m_buf2[i] -= m_buf2[i] >> 5;
}
//交換波能數據緩沖區
short[] temp = m_buf1;
m_buf1 = m_buf2;
m_buf2 = temp;
}
|
渲染:
然后我們可以根據算出的波幅數據對頁面進行渲染。
因為水的折射,當水面不與我們的視線相垂直的時候,我們所看到的水下的景物并不是在觀察點的正下方,而存在一定的偏移。偏移的程度與水波的斜率,水的折射率和水的深度都有關系,如果要進行精確的計算的話,顯然是很不現實的。同樣,我們只需要做線性的近似處理就行了。因為水面越傾斜,所看到的水下景物偏移量就越大,所以,我們可以近似的用水面上某點的前后、左右兩點的波幅之差來代表所看到水底景物的偏移量。
在程序中,用一個頁面裝載原始的圖像,用另外一個頁面來進行渲染。先取得指向兩個頁面內存區的指針 src 和 dst,然后用根據偏移量將原始圖像上的每一個象素復制到渲染頁面上。進行頁面渲染的代碼如下:
|
void rippleRender()
{
int offset;
int i = m_width;
int length = m_width * m_height;
for (int y = 1; y < m_height - 1; ++y) {
for (int x = 0; x < m_width; ++x, ++i) {
// 計算出偏移象素和原始象素的內存地址偏移量 :
//offset = width * yoffset + xoffset
offset
= (m_width * (m_buf1[i - m_width] - m_buf1[i + m_width])) + (m_buf1[i - 1] - m_buf1[i + 1]);
// 判斷坐標是否在范圍內
if (i + offset >
0 && i + offset < length) {
m_bitmap2[i] = m_bitmap1[i + offset];
}
else {
m_bitmap2[i] = m_bitmap1[i];
}
}
}
}
|
增加波源:
俗話說:無風不起浪,為了形成水波,我們必須在水池中加入波源,你可以想象成向水中投入石頭,形成的波源的大小和能量與石頭的半徑和你扔石頭的力量都有關系。知道了這些,那么好,我們只要修改波能數據緩沖區buf,讓它在石頭入水的地點來一個負的“尖脈沖”,即讓buf[x,y] = -n。經過實驗,n的范圍在(32 ~ 128)之間比較合適。
控制波源半徑也好辦,你只要以石頭入水中心點為圓心,畫一個以石頭半徑為半徑的圓,讓這個圓中所有的點都來這么一個負的“尖脈沖”就可以了(這里也做了近似處理)。
增加波源的代碼如下:
|
// stoneSize : 波源半徑
// stoneWeight : 波源能量
//
void dropStone(int x, int y, int stoneSize, int stoneWeight)
{
// 判斷坐標是否在范圍內
if ((x + stoneSize) > m_width || (y +
stoneSize) > m_height
||
(x - stoneSize) < 0 || (y - stoneSize) < 0) {
return;
}
int value = stoneSize * stoneSize;
short weight = (short)-stoneWeight;
for (int posx = x - stoneSize; posx < x +
stoneSize; ++posx) {
for (int posy = y - stoneSize; posy < y +
stoneSize; ++posy) {
if ((posx - x) * (posx - x) + (posy - y) *
(posy - y)
< value)
{
m_buf1[m_width * posy + posx] = weight;
}
}
}
}
|
如果我們想要模擬在水面劃過時引起的漣漪效果,那么我們還需要增加新的算法函數
breasenhamDrop。
|
void dropStoneLine(int x, int y, int stoneSize, int stoneWeight) {
// 判斷坐標是否在屏幕范圍內
if ((x + stoneSize) > m_width || (y +
stoneSize) > m_height
|| (x - stoneSize) < 0 || (y -
stoneSize) < 0) {
return;
}
for (int posx = x - stoneSize; posx < x +
stoneSize; ++posx) {
for (int posy = y - stoneSize; posy < y +
stoneSize; ++posy) {
m_buf1[m_width * posy + posx] = -40;
}
}
}
// xs, ys
: 起始點,xe, ye : 終止點
// size : 波源半徑,weight : 波源能量
void breasenhamDrop (int xs, int ys, int xe, int ye, int size, int weight)
{
int dx = xe - xs;
int dy = ye - ys;
dx = (dx >= 0) ? dx : -dx;
dy = (dy >= 0) ? dy : -dy;
if (dx == 0 && dy == 0) {
dropStoneLine(xs, ys, size, weight);
}
else if (dx == 0) {
int yinc = (ye - ys
!= 0) ? 1 : -1;
for(int i = 0; i <
dy; ++i){
dropStoneLine(xs, ys, size, weight);
ys += yinc;
}
}
else if (dy == 0) {
int xinc = (xe - xs != 0) ? 1 : -1;
for(int i = 0; i < dx; ++i){
dropStoneLine(xs, ys, size, weight);
xs += xinc;
}
}
else if (dx > dy) {
int p = (dy << 1) - dx;
int inc1 = (dy << 1);
int inc2 = ((dy - dx) << 1);
int xinc = (xe - xs != 0) ? 1 : -1;
int yinc = (ye - ys != 0) ? 1 : -1;
for(int i = 0; i < dx; ++i) {
dropStoneLine(xs, ys, size, weight);
xs += xinc;
if (p < 0) {
p += inc1;
}
else {
ys += yinc;
p += inc2;
}
}
}
else {
int p = (dx << 1) - dy;
int inc1 = (dx << 1);
int inc2 = ((dx - dy) << 1);
int xinc = (xe - xs != 0) ? 1 : -1;
int yinc = (ye - ys != 0) ? 1 : -1;
for(int i = 0; i < dy; ++i) {
dropStoneLine(xs, ys, size, weight);
ys += yinc;
if (p < 0) {
p += inc1;
}
else {
xs += xinc;
p += inc2;
}
}
}
}
|
效果圖:

劃過水面時的漣漪特效 | 
雨滴滴落水面特效
|
結語:
這種用數據緩沖區對圖像進行水波處理的方法,有個最大的好處就是,程序運算和顯示的速度與水波的復雜程度是沒有關系的,無論水面是風平浪靜還是波濤洶涌,程序的fps始終保持不變,這一點你研究一下程序就應該可以看出來。