src:
維基百科,自由的百科全書
跳轉到: 導航, 搜索
在計算理論中,確定有限狀態(tài)自動機或確定有限自動機(英:deterministic finite automaton;簡稱:DFA)是一個能實現狀態(tài)轉移的自動機。對于一個給定的屬于該自動機的狀態(tài)和一個屬于該自動機字母表Σ的字符,它都能根據事先給定的轉移函數轉移到下一個狀態(tài)(這個狀態(tài)有可能就是先前那個狀態(tài))。
[編輯] 基礎概念
[編輯] 定義
確定有限狀態(tài)自動機  是由
是由
- 一個非空有限狀態(tài)的集合 Q
- 一個輸入字母表 Σ(非空有限字符的集合)
- 一個轉移函數
 (例如:
(例如: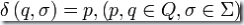 )
) - 一個開始狀態(tài)

- 一個接受狀態(tài)的集合

所組成的5-元組。因此一個DFA可以寫成這樣的形式: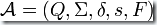 。
。
[編輯] 非正式的語義
確定有限狀態(tài)自動機一個字符接一個字符的讀入一個字符串 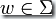 ,并根據給定的轉移函數一步一步的轉移至下一個狀態(tài)。在讀完該字符串后,如果該自動機停在一個屬于F的接受狀態(tài),那么它就接受該字符串,反之則拒絕該字符串。
,并根據給定的轉移函數一步一步的轉移至下一個狀態(tài)。在讀完該字符串后,如果該自動機停在一個屬于F的接受狀態(tài),那么它就接受該字符串,反之則拒絕該字符串。
[編輯] 擴展轉移函數
為了能夠對DFA的命題進行證明,需要一個數學上的正式的語義定義。
為此我們定義一個擴展的轉移函數 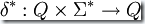 。
。
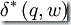 是自動機從狀態(tài)q順序讀入字符串w后達到的那個狀態(tài)
是自動機從狀態(tài)q順序讀入字符串w后達到的那個狀態(tài) - 擴展轉移函數遞歸的定義為:
[編輯] 正式的語義
對于一個確定有限狀態(tài)自動機 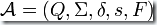 ,如果
,如果 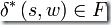 ,我們就說該自動機接受字符串w,反之則表明該自動機拒絕字符串w。
,我們就說該自動機接受字符串w,反之則表明該自動機拒絕字符串w。
被一個確定有限自動機接受的語言(或者叫“被識別的語言”)定義為: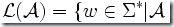 接受字符串
接受字符串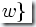 ,也就是由所有被接受的字符串組成的集合。
,也就是由所有被接受的字符串組成的集合。
[編輯] 利弊
DFA 是最實際的計算模型,因為有平凡的線性時間、恒定空間的在線算法模擬在輸入流上的 DFA。給定兩個 DFA 有有效算法找到識別它們所識別語言的并集、交集和補集 DFA。還有有效算法確定一個 DFA 是否接受任何字符串,一個 DFA 是否接受所有字符串,兩個 DFA 是否識別同樣的語言,和對特定正則語言找到有極小數目個狀態(tài)的 DFA。
在另一方面,DFA 在可識別的語言上有嚴格的限制 — 很多簡單的語言,包括需要多于恒定空間來解決的任何問題,不能被 DFA 識別。經典的 DFA 不能識別的簡單語言的例子是括號語言,就是由正確配對的括號組成的語言,比如 (()())。由形如 anbn 的字符串組成的語言,就是有限數目個 a,隨后是相等數目個 b。可以證明沒有 DFA 有足夠狀態(tài)來識別這種語言。
[編輯] 其它
1. 能被確定有限狀態(tài)自動機識別的語言是正則語言。
2. 確定有限狀態(tài)自動機是非確定有限狀態(tài)自動機的一種極限形式。
3. 確定有限狀態(tài)自動機在計算能力上等價于非確定有限狀態(tài)自動機。
4. 沒有接受狀態(tài)列表并沒有指定開始狀態(tài)的確定有限狀態(tài)機叫做轉移系統(tǒng)或半自動機。
[編輯] 例子
下面是一個確定有限狀態(tài)自動機的例子。
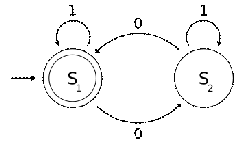

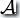 的狀態(tài)圖
的狀態(tài)圖
確定有限狀態(tài)自動機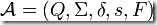
- Q = {S1,S2}
- Σ = {0,1}
- s = S1
- F = {S1}
- δ 由下面的狀態(tài)轉移表定義:
- 對應的轉移函數為:
- δ(S1,0) = S2
- δ(S1,1) = S1
- δ(S2,0) = S1
- δ(S2,1) = S2
狀態(tài)S1表示在輸入的字符串中有偶數個0,而S2表示有奇數個0。在輸入中1不改變自動機的狀態(tài)。當讀完輸入的字符串的時候,狀態(tài)將顯示輸入的字符串是否包含偶數個0。
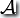 能識別的的語言是
能識別的的語言是 。用正則表達式表示為:(1 * (01 * 0) * ) * 。
。用正則表達式表示為:(1 * (01 * 0) * ) * 。
[編輯] 封閉性及一些運算
[編輯] 封閉性
確定有限狀態(tài)自動機的交,并,差,補,連接,替換,同態(tài),逆同態(tài)等運算是封閉的,也就是說確定有限狀態(tài)自動機通過這些運算產生的新的自動機也是確定有限狀態(tài)自動機。
[編輯] 補運算
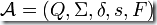 是一個DFA,那么由補運算產生的新DFA定義為:
是一個DFA,那么由補運算產生的新DFA定義為: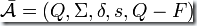 。顯然只要將
。顯然只要將 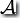 中接受的狀態(tài)設為不接受的狀態(tài),同時把不接受的狀態(tài)設為接受的狀態(tài)就得到
中接受的狀態(tài)設為不接受的狀態(tài),同時把不接受的狀態(tài)設為接受的狀態(tài)就得到 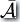 。補運算的復雜度是:
。補運算的復雜度是: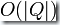 。
。
[編輯] 交運算和并運算
有兩個DFA,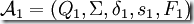 和
和 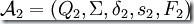 ,那么由這兩個DFA創(chuàng)造出來的新的自動機定義為:
,那么由這兩個DFA創(chuàng)造出來的新的自動機定義為: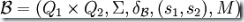 。其中
。其中 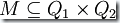 ,
,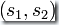 為
為  的開始狀態(tài),
的開始狀態(tài),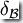 為
為  的轉移函數,且作如下定義:
的轉移函數,且作如下定義: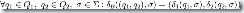 。
。
1. 當 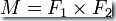 時,由上述方法得到的
時,由上述方法得到的  就是DFA
就是DFA 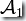 和
和 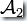 的交運算,記作:
的交運算,記作: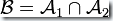 。也就是說對于讀入的字符串w,當且僅當
。也就是說對于讀入的字符串w,當且僅當 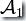 和
和 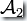 同時接受w的時候
同時接受w的時候  接受w。
接受w。
2. 當 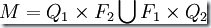 時,由上述方法得到的
時,由上述方法得到的  就是DFA
就是DFA 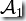 和
和 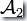 的并運算,記作:
的并運算,記作: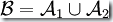 。也就是說對于讀入的字符串w,只要
。也就是說對于讀入的字符串w,只要 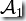 或
或 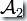 中至少有一個接受w,
中至少有一個接受w,  就接受w。
就接受w。
交運算和并運算的復雜度都是  。
。
[編輯] 同態(tài)和逆同態(tài)運算
一個同態(tài)函數 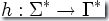 可以遞歸的定義為:
可以遞歸的定義為:
于是則有 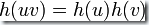 。(以上所述中
。(以上所述中 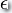 為空字符,
為空字符,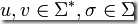 )
)
1. 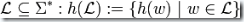 :對于接受語言L的DFA,只要將其中代表
:對于接受語言L的DFA,只要將其中代表 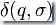 的邊替換成一個序列
的邊替換成一個序列 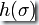 并在其中加入不屬于原DFA狀態(tài)的新狀態(tài),就產生了接受語言h(L)的DFA。
并在其中加入不屬于原DFA狀態(tài)的新狀態(tài),就產生了接受語言h(L)的DFA。
2. 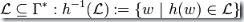 :定義一個
:定義一個 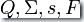 都不變的新DFA,并定義新的轉移函數為
都不變的新DFA,并定義新的轉移函數為 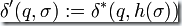 ,則
,則 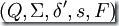 就是逆同態(tài)運算產生的新DFA。
就是逆同態(tài)運算產生的新DFA。
此外替換運算和逆同態(tài)運算的方法近似。
[編輯] 最小自動機
[編輯] 等價類自動機
對于一個正則語言,接受該語言的等價類自動機是一個 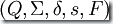 的5-元組。其定義如下:
的5-元組。其定義如下:
~L 被稱為Nerode關系,是Myhill-Nerode定理的基礎。簡單的來說就是對于任意 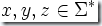 ,如果
,如果  ,那么 x~Ly 。
,那么 x~Ly 。
[編輯] 唯一性
對于任意給定的確定有限狀態(tài)自動機都能找到一個與之計算能力等價的最小確定有限狀態(tài)自動機,簡稱最小自動機。該最小自動機中狀態(tài)的數量等于能識別相同語言的等價類自動機中等價關系的數量,我們可以稱最小自動機和等價類自動機“實際上”是相等的,也就是同構。非正式的說法是:對于最小自動機上的任意狀態(tài)都可以通過一個同構函數變換成等價類自動機上的一個狀態(tài)。
能識別一個正則語言的等價類自動機是唯一的,因此能識別該語言的最小自動機也是唯一的。
[編輯] 算法
定義一個非等價關系: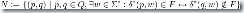 ,如下步驟可以得到這個集合N:
,如下步驟可以得到這個集合N:
1. 如果 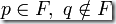 ,就給所有的狀態(tài)對(p,q)和(q,p)打上標記
,就給所有的狀態(tài)對(p,q)和(q,p)打上標記
2. 重復步驟3,直到所標記的狀態(tài)對沒有變化為止
3. 對于未標記的狀態(tài)對(p,q)和σ,如果  被標記過了就把(p,q)也標記上
被標記過了就把(p,q)也標記上
4. 以上所有標記了的狀態(tài)對的集合就是非等價關系N
以下是由一個任意DFA轉換到一個最小DFA的步驟:
1. 把所有不能從開始狀態(tài)達到的狀態(tài)刪除
2. 通過上述標記算法計算非等價關系N
3. 一步一步將不屬于N的狀態(tài)對中的兩個狀態(tài)合成一個狀態(tài)
這樣就得到了接受相同語言的最小自動機。復雜度為 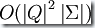 。
。
[編輯] 參見
[編輯] 引用
- Michael Sipser, Introduction to the Theory of Computation. PWS, Boston. 1997. ISBN 0-534-94728-X. Section 1.1: Finite Automata, pp.31–47. Subsection "Decidable Problems Concerning Regular Languages" of section 4.1: Decidable Languages, pp.152–155.4.4 DFA can accept only regular language
來自“http://zh.wikipedia.org/wiki/%E7%A1%AE%E5%AE%9A%E6%9C%89%E9%99%90%E7%8A%B6%E6%80%81%E8%87%AA%E5%8A%A8%E6%9C%BA”