最近得做一些跟自動機有關的東東,其中一部分可以簡要地看作是由一套正則文法生成狀態自動機的過程。
什么是正則表達式?
首先我們看看什么是正則表達式。這個東東呢,一般用于描述一個字符串的集合——直接說就是一個正則表達式可能可以匹配一大堆字符串,而這一大堆字符串可以形成一個集合,它們的共同特征就是可以被這個正則表達式匹配。就像去死去死團�����,但是不同的是去死去死團的團員的共同特征是不被任何異性所匹配——但是這沒關系����,我們不妨取去死去死團的補集就行了。
反正正則表達是很好啦�����,因為你只要用一點點在臟話里����,就可以罵好多好多人����,比如:
Mar(y|k|cus) is son of bitch.
真是非常de省力,唯一的缺點是可能對方不知道你在說什么��。
好了�����,從上面我們可以看出正則表達式中的兩個基本結構:
· 連結 (Concatenation)�����,比如 bitch,由b, i, t, c, h連接而成
· 聯合 (Union),比如 y|k|cus����,可以認為是y或k或者cus
下面是第三個基本結構����,被稱為Kleene star (或者 Kleene 閉包)的。因為這個操作是Stephen Cole Kleene發明的�����。啊啊��,其實正則表達式這個東西就是Kleene發明的��。這個同學真是非常的牛B����,因為他是更加牛B的 阿隆佐 - 丘奇 ( Alonzo Church )——歷史上和阿蘭 - 圖靈 ( Alan Turing ) 并稱的人物——的學生。有多牛B呢��,這個Kleene還和他的老師��,還有圖靈����,就遞歸論發表了論文��,奠定了可計算理論的根基��。啊哈哈哈,真是牛B啊。
嗯,所謂Kleene Star的例子就是這樣的��。
· Kleene Star�����,比如a*��,可以接受空串和若干個a連結組成的串
當然咯,還有一些別的操作��,比如我們知道的+��,?��,集合[]等等,但是這些操作都可以通過上面三個基本操作的組合來完成�����。
比如+����,a+可以認為是aa*
什么是NFA��?
要說NFA嘛��,我得先說說DFA。所謂DFA�����,就是Deterministic Finite state Automata的簡稱����。是狀態機的一種。通俗的說�����,就是一大堆狀態的集合��,里面有一個初始狀態和若干終止狀態����,每個狀態可以有若干個輸出邊前往別的狀態��。但是要求每個狀態的同一種輸出邊至多只有一個�����,所以自動機被稱為是”Deterministic”的��。
比如下面這個例子:
表述的是一個電燈de開關,這個開關每按一下就從’開’狀態轉換到’關’狀態,或者從’關’狀態轉換到’開’狀態����。而為了從環保角度出發��,在’關’狀態才被認為是終止態��。
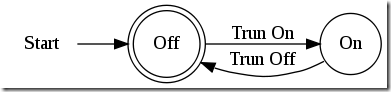
上面的自動機呢��,就可以描述這個燈泡的行為模式,或者說可以描述電燈的狀態轉換過程����。輸出邊就是’開’或者’關’的動作��,或者說這個燈泡的開關,只接受這兩種動作:“Trun On”����,“Trun Off”����。而”Trun On”動作只會導致燈的狀態變成“On”��,“Trun Off”動作只會導致燈的狀態變成“Off”��,這是確定的,你的外婆都可以預料到的��。所以說DFA是確定有限狀態自動機�����。
現在可以說NFA了��。這個NFA嘛,全稱是Non-deterministic Finite state Automata����。也是狀態自動機的一種��。確切地說,剛才的DFA是NFA的一個子集�����。和DFA唯一的區別就是他是”Non-deterministic”的��,哈,非確定的�����,每個狀態的同一種輸出邊可以不止一個�����。
還是用剛才的例子?�,F在假設我們的電燈有一種新的狀態咯~:壞掉了。燈絲被過大的電流燒斷了�����,聽上去遭透了��,因為一”Trun On”就得準備換燈泡了:
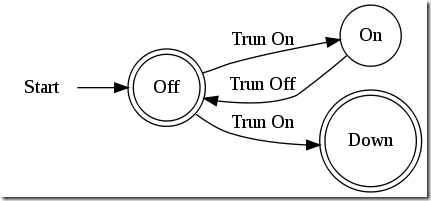
但是我們沒法確定的知道哪一次Trun On會導致燈泡壞掉��,使得燈泡進入”Down”狀態的那次“開”操作看上去跟你昨天開燈的那次操作一模一樣(嚴格的說,每一次點亮燈泡都會導致燈絲的狀態發生變化����,但是在此簡化了)
所以從狀態”Off”出來的輸出邊中����,”Trun On”有兩條�����,這就導致沒法根據當前狀態和輸出邊確定下一狀態����,這就是為什么稱為非確定性有限自動機的原因��。
如何轉換����?
剛才Shellex說了����,正則表達式有三種基本結構。如果能先將這三種基本結構轉換成對應的NFA����,然后在用這三種基本結構去拼裝成完整的NFA是不是很省力呢����?
下面就是三種基本正則表達式的NFA
ab:

a*:
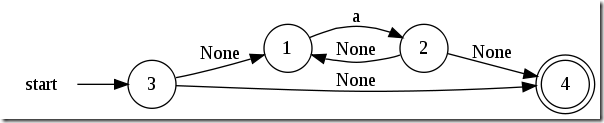
a|b:
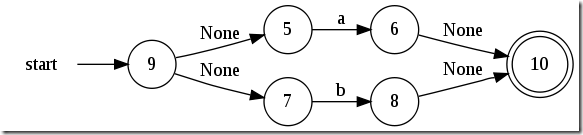
里面出現了一種叫“None”的邊����。這個不代表這個邊是字面上的“None”,而是指這個邊是個空邊。也就是說任何“動作”都可以從這個邊進入下一個狀態�����。它的學名叫 epsilon 邊��,一般表示成’ε’��,Shellex這里表示成“None”了。
下面我們來考慮正則表達式到NFA轉換。給出一個正則串的輸入,得到一個NFA的輸出�����。被廣泛采用的是Thompson Algorithm��,也就是所謂的子集算法。該算法的發明人應該就是寫ed編輯器的那個Thompson大牛。該算法的實現和算術表達式的求值非常的類似,需要一個符號棧存放操作符��,一個自動機棧存放生成的自動機��。算法結束后��,可以從自動機棧中Pop一個最終的結果。
比如對于正則表達式(a|b)*cd,求值過程如下:
PUSH a To automaton stack
PUSH b To automaton stack
UNION
STAR
PUSH c To automaton stack
CONCAT
PUSH d To automaton stack
CONCAT
POP result
里面的UNION��,STAR 和 CONCAT就是三種基本結構的生成操作了�����。而這三種基本操作的實現是這樣的:
Star:
POP T from automaton stack
CREATE state A, B
ADD transition from A to B with 'ε'
ADD transition from A to T.entry with 'ε'
ADD transition from T.exit to A with 'ε'
ADD transition from T.exit to B with 'ε'
ADD state A, B to T
PUSH T to automaton stack
Concat:
POP F, S from automaton stack
ADD transition from F.exit to S.entry with 'ε'
JOIN S to F
SET F.exit = S.exit
SET F.inputSet += S.inputSet
PUSH F to automaton stack
Union:
POP F, S from automaton stack
CREATE state A, B
ADD transition from A to F.entry with 'ε'
ADD transition from A to S.entry with 'ε'
ADD transition from T.exit to B with 'ε'
ADD transition from T.exit to B with 'ε'
JOIN S to F
ADD state A, B to T
SET F.exit = S.exit
SET F.inputSet += S.inputSet
PUSH F to automaton stack