詞法分析(1)---詞法分析的有關概念以及轉換圖
詞法分析是編譯的第一個階段,前面簡介中也談到過詞法分析器的任務就是:
字符流------>詞法記號流
這里詞法分析和語法分析會交錯進行,也就是說,詞法分析器不會讀取所有的詞法記號再使用語法分析器來處理,通常情況下,每取一個詞法記號,就送入語法分析器進行分析,圖解:
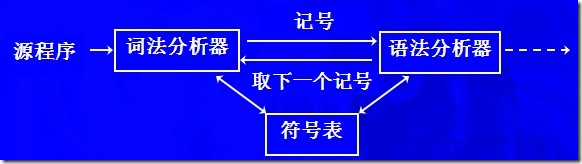
詞法分析器是編譯器中與源程序直接接觸的部分,因此詞法分析器可以做諸如
1). 去掉注釋,自動生成文檔(c#中的///注釋)
2). 提供錯誤位置(可以通過記錄行號來提供),當字符流變成詞法記號流以后,就沒有了行的概念
3). 完成預處理,比如宏定義
1. 詞法記號,詞法單元(lexeme),模式
模式是一種規則
每個詞法單元都有一個特定記號
比如 int a=3,這里 int,a,=,3都是詞法單元,每個詞法單元都屬于某個詞法記號,比如3就是"num"這個詞法記號的一個詞法單元,而模式規定了什么樣的字符串的詞法記號是什么樣的(模式是一種規則)
某一特定模式規定了某個詞法記號下的一類詞法單元,比如:
模式:用字母開頭的包含字母和數字的串
上面模式的詞法記號:id(所有符合上面模式的字符串的記號都是id)
詞法單元:a123 或者 aabc 等
詞法記號舉例(簡稱為記號):
1) 每個的關鍵字都有屬于自己的一個記號,比如關鍵字for,它可以使用記號for;關鍵字int,可以使用記號int
2) 所有的關系運算符只有一個記號,比如 >=,<=都用記號relation
3) 所有的標識符只有一個記號,比如a123,aab使用記號id
4) 所有的常數只有一個記號,比如123,22,32.3,23E10使用記號num
5) 所有的字符串只有一個記號,比如"123","ab1"使用記號literal
在實際的編譯器設計中,詞法記號,一般用一個整形數字表示
詞法記號的屬性:
我們喜歡用<詞法記號, 屬性>這個二元組來描述一個詞法單元,比如,對于源代碼:position := initial + rate * 60
對于詞法單元 +,我們可以使用 <add_op, '+'> 來表示。
有些情況,更加復雜一點,比如對于 position,我們表示是這樣的,<id, 指向符號表中的position元素的指針>,詳細來說應該是這樣的,假定屬性是一個字符串,那么id將指向這樣一個字符串"position\0",我們把存放這個字符串的地方叫做符號表。有些時候,屬性是不必要的,比如 := ,表示賦值,我們可以使用 <assign_op,257> 這樣的表示這個詞法單元,不過這個顯得有些多于,因為assign_op和詞法單元是一對一的,也就是assign_op只對應了:=,所以額外信息(屬性)就顯得多余的了
詞法錯誤:
詞法分析器是很難(有些錯誤還是可以檢測)檢測錯誤的,因為詞法分析器的目的是產生詞法記號流,它沒有能力去分析程序結構,因此無法檢測到和程序結構有關的錯誤,比如:
fi(a == b)
詞法分析器不會找到這個錯誤,它認為 fi 是一個標識符,而不是一個關鍵字,只有在后面的階段中,這個錯誤才會被發現,這是一個與程序結構有關的錯誤
詞法分析器,只能檢測到詞法單元上的問題,比如 12.ab ,作為一個詞法單元,卻不沒有對應的模式,那么就是產生一個錯誤。
2. 正規式:
前面說過模式是一種規則,為了使用,我們需要一種規范的方式來表達模式,這就是正規式
1) 串和語言
字符類(又叫字母表):關于字符的有限集合
串:字符類上字符的有窮序列,串這個概念,具體來說是,某個字符類上的串
串的長度:串中字符的個數,比如串 s = abc ,那么串的長度為3,用|s|表示串的長度
空串:用 ε 表示
語言:某字符類上的串的集合,屬于語言的串,成為語言的句子或字
比如:{abc, a}這就是一個語言,abc和a就是句子。另外空集也是屬于語言
連接:x是串,y是串,x和y連接,結果就是 xy 這個串。假如 x 是串,x^3為 xxx。對于 x^n (n>=0),x^0 = ε
語言的運算(假定L和M是語言):
1. L U M = {s|s屬于L或者M},例如:
L={1,2} M={3,4} 那么 L U M = {1,2,3,4}
2. LM = {st|s屬于L且t屬于M},例如:
L={a,b} M={1,2} 那么 LM = {a1,a2,b1,b2} ML={1a,1b,2a,2b}
3. L^n = LLL...LLL (n個L),例如:
L={a,b} 那么 L^3 = {aaa,aab,aba,abb,baa,bab,bbb,bba}
注意 n 可以為0,L^0 = {ε}
4. L* = L^0 U L^1 U L^2 U L^3 U ...
L*表示,語言L中,所有的句子(串)以任意數目任意順序組成的句子的集合,包括 ε,例如:
{a,b}* = {ε,a,b,ab,ba,aab,aba,baa,bba,bab,abb,aaa,bbb...}
L*叫做L的閉包
5. L+ = L^1 U L^2 U L^3 U...
L+表示,語言L中,所有的句子(串)以任意數目任意順序組成的句子的集合,但是不包括 ε
L+中的句子和 L*中的句子相比少一個 ε
那么,我們通過上面的知識就可以表示一個標識符了,我們知道一般語言規定標識符是由字母開頭,后接若干個字母或數字,我們可以這樣來表示: L={a-z A-Z} N={0-9},那么標識符就是 L(L U N)*
2) 正規式
正規式又叫正規表達式,正規式是模式得一種規范的表達形式,正規式描述了一個集合,這個集合是由串組成的,其實這個集合就是我們前面說過的語言,不過這里大家喜歡使用正規集這個術語。正規式 r 表示正規集L(r)
正規式的運算:
1. 閉包運算,運算優先級最高,(r)* 表示 (L(r))*
2. 連接運算,運算優先集合低于閉包,(r)(s) 表示 (L(r))(L(s))
3. 或運算,運算優先集合最低,(r) | (s) 表示 (L(r)) U (L(s))
例如:
a | b 表示集合(語言,正規集) {a,b}
(a | b)(a | b) 表示集合(語言,正規集) {aa,ab,ba,bb}
a* 表示由一切a字符組成的集合(語言,正規集),包括 ε
(a | b) 表示由a,b組成的集合(語言,正規集),包括 ε
等價的正規式:(a | b) = (b | a)
正規式的代數性質:
1. r|s = s|r
2. r|(s|t) = (r|s)|t
3. (rs)t = r(st)
4. r(s|t) = rs|rt
5. εr = r
6. r** = r*
7. r* = (r|ε)*
注意,rs != sr 因為連接運算是有順序的,記住并理解2個最基本的運算:a|b表示{a,b},ab表示{ab}
3. 正規定義
我們可以使用 名字 -> 正規式這種表示,來說明一個等價的代替,比如:
dight -> 0|1|2|3|4|5|6|7|8|9
這里,我們就可以使用名字 digit 來代替后面的正規表達式
我們可以對某個串集進行正規定義,比如我們對標識符集合進行正規定義:
letter -> A|B|...|Z|a|b|...|z
dight -> 0|1|2|3|4|5|6|7|8|9
id -> letter(letter|dight)*
請通過上面的例子理解正規定義。
在我們表達正規表達式的時候,可以使用一些符號使得表達簡化
1) + ,表示一個或者多個實力,比如,a+ 表示 {a,aa,aaa,aaaa,...}。區別一下*,他們的關系是這里 r+ = r* | ε
2) 字符組,[abc]表示a|b|c,還可以這樣表示[a-zA-Z]表示字母表中的字符
4. 狀態轉換圖
狀態轉換圖是對詞法分析器進行分析過程的描述,我們看一個判斷關系運算的狀態轉化圖:
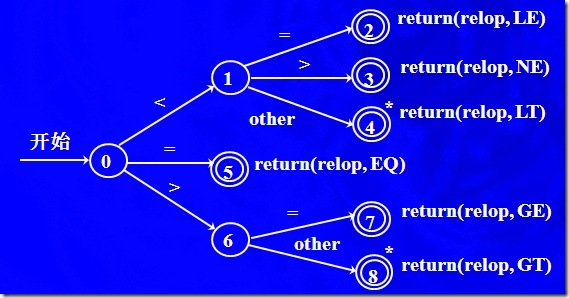
1) 圖中圓圈表示狀態
2) 箭頭叫做邊。X狀態的邊,一般指的是由X狀態出發,指向其他狀態的邊
3) 邊上的符號叫做標記
如何來使用這個圖?假定輸入字符串是 <= ,那么識別開始時,發現 < 和狀態0與狀態1間的邊上的標記一樣,那么就進入1狀態,下一個輸入字符為=,將進入2狀態,識別結束,返回二元組<relop,LE>
上圖中2,3,4,5,7,8狀態,他們表示識別了一個關系運算符,這個狀態叫做接受狀態
狀態4上面有一個*,表示說,輸入指針需要回移。所謂的輸入指針,就是指向輸入字符串中現在被讀入的字符的位置,4狀態會多讀取一個字符,所以需要回移,也就是要注意的是,識別完成之后,輸入指針指向的是被識別對象的最后一個字符,而不是待識別對象的第一個字符,這樣的規定在實現詞法分析器時,是有一定的意義,舉例說明:
輸入字符串為: a>b
識別的時候,從>開始,讀入下一個字符b時,進入4狀態,這個時候,輸入指針指向b,這時候需要回移
我們在需要回移的狀態上加一個*
每個狀態后面有一個return(relop,XX)這個是狀態的行為,這里具體來說就是返回一個二元組的行為,詞法分析器分析的結果就是得到二元組(詞法記號和屬性的二元組),這個二元組可以表示一個特定的字符串。其實上面的*,也是表示行為,也就是輸入指針回移的行為,我們可以看見,只有在接受狀態才會有行為出現
對一門典型的語言來說狀態可能有幾百個
5. 如何編寫一個詞法分析器
1) 根據需要寫出正規定義
2) 根據正規定義畫出轉換圖
3) 根據轉換圖寫出詞法分析器
這里詳細討論面向過程的語言來實現一個詞法分析器(比如c語言),并且主要討論的是第3步
1) 我們需要一個 nextchar() 函數,取得緩存中下一個等待分析的字符,這個函數完成年2個任務
1. 讓輸入指針向前移動一位
2. 返回輸入指針指向的字符
2) 定義一個變量 token_beginning,在每個狀態轉換圖開始的時候,記錄輸入指針的位置,定義forward變量作為輸入指針
3) 狀態轉換圖被實現成為代碼之后,每個狀態都有屬于自己的一塊代碼,這些代碼按順序完成以下工作:
1. 讀取一個字符,通過nextchar()函數
2. 讀取的字符(標志),如果它和當前狀態的邊上的標記相同,那么狀態將轉換到邊所指向的狀態,具體實現只需要一個語句就是 state = xxx(xxx為目標狀態);如果當前狀態的所有邊的標記和這個讀取字符不一樣,那么表示沒有找到token(詞法記號),這時候需要調用 fail() 函數
3. fail() 函數完成這樣的功能:a.指針回移,完成 forward = token_beginning 的操作 b.找到適當的開始狀態(也就是尋找另外一個轉換圖的開始狀態)。假定所有的轉換圖都被嘗試過,并且無法匹配,這時候會調用一個發現錯誤的小程序,來報告錯誤
4. 請不要隨意添加行為到各個狀態所持有的代碼中,應該以轉換圖中表示的行為為準
4) 定義一個全局變量 lexical_value,用于保存一個指針,這個指針由 install_id() 和 install_num() 兩個函數中的一個返回
5) 定義兩個整形變量 start,state,分別表示一個轉換圖的開始狀態和當前的狀態
6) nexttoken(),這是詞法分析器的主程序,可以說,我們通過調用nexttoken()就完成了詞法分析,這個函數一定是這樣的格式:
while(1){
switch(state){
case xx:
...
case yy:
...
default:
...
}
}
關于詳細的設計這里就不說了,舉例說明一個轉換圖如何轉換成為程序:
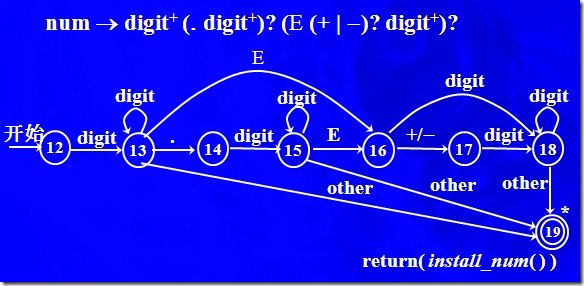
這是一個識別浮點數的例子,看下面的代碼:
#include <stdio.h>
#include <ctype.h>
#include <string.h>
char *nexttoken();
char nextchar();
void next();
void back();
char* gettoken();
char cbuf[]="12.3*********klj12.2e2jj778";
int forward = -1;
int main(){
while(1){
printf("%s\n",nexttoken());
if(forward >= strlen(cbuf)-1){
getchar();
return 0;
}
}
}
int state;
int start;
char* nexttoken(){
char c;
state = 12;
while(1){
switch(state){
case 12:
c = nextchar();
start = forward;
if(isdigit(c)){
state = 13;
}else{
next();
}
break;
case 13:
c = nextchar();
if(isdigit(c))
state = 13;
else if(c == 'e'||c == 'E')
state = 16;
else if(c == '.')
state = 14;
else
state = 19;
break;
case 14:
c = nextchar();
if(isdigit(c))
state = 15;
break;
case 15:
c = nextchar();
if(isdigit(c))
state = 15;
else if(c == 'e'|| c == 'E')
state = 16;
else
state = 19;
break;
case 16:
c = nextchar();
if(isdigit(c))
state = 18;
else if(c == '+' || c == '-')
state = 17;
break;
case 17:
c = nextchar();
if(isdigit(c))
state = 18;
break;
case 18:
c = nextchar();
if(isdigit(c))
state = 18;
else
state = 19;
break;
case 19:
back();
return gettoken();
}
}
}
char nextchar(){
forward ++;
return cbuf[forward];
}
void back(){
forward --;
}
void next(){
forward ++;
}
char token_buf[128];
char* gettoken(){
int i,j=0;
for(i = start; i <= forward; i ++){
token_buf[j++] = cbuf[i];
}
token_buf[j] = '\0';
return token_buf;
}
詞法分析(2)---NFA
假定一個輸入符號(symbol),可以得到2個或者2個以上的可能狀態,那么這個finite automaton就是不確定的,反之就是確定的。例如:
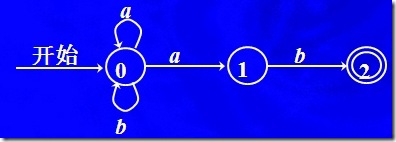
這就是一個不確定的無限自動機,在symbol a輸入的時候,無法確定狀態應該轉向0,還是1
不論是確定的finite automaton還是非確定的finite automaton,它們都可以精確的描述正規集(regular sets)
我們可以很方便的把正規表達式(regular expressions)轉換成為不確定 finite automaton
2. NFA(Nondeterministic Finite Automaton)
非確定的無限自動機,我們用NFA這個術語表示,它是一個數學模型(model):
1. 一個關于狀態的集合S
2. 一個關于輸入符號(input symbols)的集合Σ
3. 函數 move : (狀態, 符號) -> P(S)
4. 一個開始狀態s0,是一個唯一的狀態
5. 一個結束(接受)狀態集合F
注意,P(S),表示S的冪集。在NFA中,input symbol可以為 ε
轉換函數(transition function)的含義就是,一個確定的狀態已經從這個狀態出發的一條邊的標簽(符號symbol),可以確定它的下一個狀態組成的集合,比如上圖(這個轉換圖就是NFA的一種表示方式),0狀態,a符號,確定了一個狀態的集合{0,1}
3. 轉換圖(transition graph)的表示
我們知道,計算機是無法直接表示一個圖,我們應該如何來表示一個轉換圖?使用表格就是一個最簡單的方法,每行表示一個狀態,每列表示一個input symbol,這種表格被叫做 transtion table(轉換表)
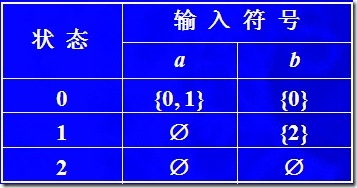
可以說使用表格是最簡單的表示方式,但是我們可以注意到在這個圖中狀態1和input symbol a,是沒有下一個狀態的(空集合),也就是,對于一個大的狀態圖,我們可能花費大量的空間,而其中空集合會消耗不少空間,但是這種消耗又不是必須的,所以,作為最簡單的一種實現方式,卻不是最優的
語言(language)被NFA定義成為一個input string的集合,而這個集合中的元素則是被NFA受接受的所有的字符串(那些可以從開始狀態到某接受狀態的input string)
至于存儲的方式,可以試試鄰接表。注意,使用什么樣的數據結構來保存NFA按情況不同而不同,在一些特殊情況下,某些數據結構會變得很方便使用,而換入其他情況,則不可以使用了。
詞法分析(3)---DFA
1. DFA(Deterministic Finite automaton)
DFA就是確定的有限自動機,因為DFA和NFA關系密切,我們經常需要把他們拿到一起來講,NFA可以轉化成為一個DFA,DFA依然是一個數學model,它和NFA有以下區別
1. 不存在ε-transition,也就是說,不存在ε為input symbol的邊
2. 對于move函數,move : (state, symbol) -> S,具體來說就是,一個狀態和一個特定的input symbol,不會映射到2個不同的狀態。這樣的結果是,每個狀態,關于每個特定的input symbol,只有一條出邊
下圖就是一個DFA:
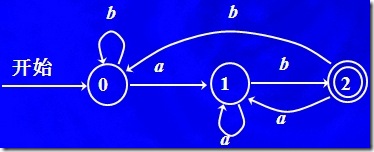
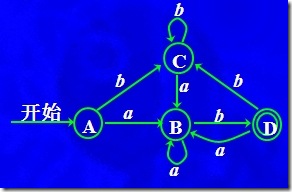
接受語言(a|b)*ab,注意一下,接受語言(a|b)*ab的DFA我們前面見過,就是這張圖:
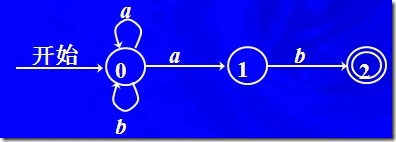
2. DFA的行為
我們用一個算法來模擬DFA的行為
s = s0;
c = nextchar();
while(c != EOF){
s = move(s,c);
c = nextchar();
}
if(s屬于F)
return "yes"
else
return "no"
詞法分析(4)---NFA與DFA的轉化
1. 子集構造(Subset Construction)
這是一個轉換NFA到DFA的算法。我們知道NFA和DFA的區別最主要的就是一個狀態和一個input symbol是否能夠確定一個狀態的問題,對于NFA,它將確定一個組狀態,而DFA將確定一個狀態,因此,我們有一個很好的辦法就是把NFA的狀態集對應每個DFA的狀態,這就是subset construction的思想,不過這只是大概泛泛而論,我們需要更加明確的認識
1) NFA在任何一個input symbol下,映射的狀態集(通過move函數,這個集合通常用T字母表示)應該被知道
2) 必須保證1)中狀態集都對應了DFA中的一個狀態
具體算法:
Input : 一個NFA N
Output : 接受相同語言的DFA D
Method : 為D構架一個transition table(轉換表) Dtran,每個DFA的狀態是一個NFA的狀態集合(這里一定要注意前面說過的1)2)兩點)。我們定義一些操作:
s 表示NFA的狀態,T 表示NFA的狀態集合,a表示一個input symbol
ε-transition(ε轉換)就是說input symbol為ε時的transition(轉換)
| 操作(operation) | 描述(description) |
| ε-closure(s) | 從NFA的狀態s出發,只通過ε-transition到達的NFA的狀態集合 |
| ε-closure(T) | NFA的集合T中的狀態p,只通過ε-transition到達的NFA的狀態集合,再求這些集合的交集。用數學表達就是 {p|p 屬于 ε-closure(t) , t屬于T} |
| move(T,a) | NFA的集合,這個集合在input symbol為a,狀態為T中任意狀態情況下,通過一個轉換得到的集合 |
注意一下,所有的操作都是針對NFA的狀態或者狀態集合,得到的時NFA的狀態集合,或者說是DFA看為一個狀態
Subset Construction
初始Dstates,它僅僅含有狀態(D的狀態)ε-closure(s0),并且狀態未被標記,s0表示開始狀態,注意,Dstates放的是D的狀態
while ( Dstates 有未標記的狀態 T ) { // T是D中的一個狀態,也是N中一個狀態集
標記 T;
for ( input symbol a ){ // 遍歷所有的input symbol
U = ε-closure(move(T, a)); // move為NFA的move函數
if ( U 不在 Dstates 中 )
把U作為尚未標記的狀態加入Dstates;
Dtran[T, a] = U
}
}
注意,狀態s,ε-closure(s)一定包含s
我們先來熟悉上面的操作operation,再來看上面的算法

ε-closure(0) = {0, 1, 2, 4, 7} // 從0狀態出發的,input symbol為ε的所有狀態的集合
ε-closure(3) = {1, 2, 3, 4, 6, 7}
ε-closure(8) = {8}
ε-closure( {3, 8} ) = ε-closure(3) U ε-closure(8) = {1, 2, 3, 4, 6, 7, 8}
move(0,a) = 空
move(7,a) = {8}
move(8,b) = {9}
move( {0, 1, 2, 4, 7}, a) = move(0,a) U move(1,a) U move(2,a) U move(4,a) U move(7,a) = {3, 8}
現在可以回去理解一下算法了。
這里再說說求ε-closure(T)的算法:
把T的所有狀態壓入stack(棧);
ε-closure(T)的初始值為 T 中的所有元素 ; // 也就是一定包含他們本身
while( 棧非空 ) {
彈出棧頂元素 t ;
for( 每個屬于 move(t, ε) 的狀態 u ){
if( u 不在 ε-closure(T) 中 ){
u 加入 ε-closure(T);
把 u 入棧;
}
}
}
下面對上圖如何使用Set Construction算法來構建DFA做一個詳細的描述:
1. 初始化Dstates 把集合 ε-closure(s0) = {0, 1, 2, 4, 7}作為第一個狀態,設此狀態為 A
2. 現在轉化,input symbol {a, b},因此,求:
ε-closure(move(A, a));
ε-closure(move(A, b));
這里會得到2個狀態
ε-closure(move(A, a)) = {1, 2, 3, 4, 6, 7, 8},設其為 B
ε-closure(move(A, b)) = {1, 2, 4, 5, 6, 7}, 設其為C
B,C放入Dstates
改寫 Dtrans
最終得到的 Dtrans 為:
A = {0, 1, 2, 4, 7}
B = {1, 2, 3, 4, 6, 7, 8}
C = {1, 2, 4, 5, 6, 7}
D = {1, 2, 4, 5, 6, 7, 9}
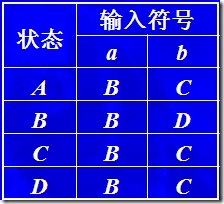
因此,NFA轉化成為DFA:
詞法分析(5)---從正規式到NFA
在說到這個問題前,先告訴大家,我們可以直接從 Regular expression 到 DFA,不過這里我們先不討論這個問題
關于RE到DFA的算法有很多,這里學習一個最簡單的
Algorithm Thompson's construction:
Input : 一個字母表(Σ)上的 Regular Experssion r
Output : 一個接受 L(r) 的 NFA N
Method : 把 r 解析成為子表達式(subexpressions),然后使用下面的1),2)規則,為 r 中的基本符號(basic symbols,基本符號就是ε和Σ中的字符)構建NFA,基本符號符合1),2)關于正規式的定義,注意,假如symbol a 出現多次,那么它每次出現都要構建一個NFA。之后,我們需要通過 r 的語法結構,通過規則3)組合前面構建的NFA,直到得到整個NFA為止。對于中間產生的NFA,它只有一個終態,沒有進入開始裝狀態的邊,也沒有離開接受狀態的邊。
1) 對于 ε 構造如下NFA
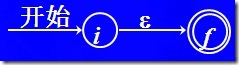
注意,每次構建時,i,f的值都不一樣,因此可見構造一個識別 ε 的NFA,會產生2個新的狀態
2) 對于Σ中的每個字符a

同樣,對于aaa,第一個a構造的NFA中的i,f不會和第2個a構造的i,f一樣,因此可見構造一個識別Σ中的每個字符a 的NFA,會產生2個新的狀態
3) 先假定 N(t) N(s) 分別是 t s 的NFA,則:
a) 對于表達式 s|t 構建 NFA N(s|t)
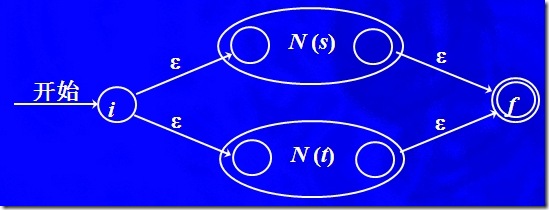
這里一樣會產生2個新的狀態i,j,我們看其中一個N(s),左邊的圓圈,表示N(s)的開始狀態,右邊的圓圈表示N(s)的接受狀態,N(t)同理
b) 對于表達式 st ,構建N(st)
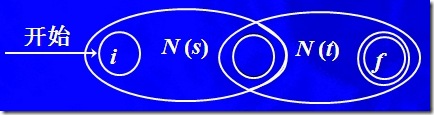
這個時候,不產生新的狀態,N(s)的開始狀態變為N(st)的開始狀態,N(t)的接受狀態變成N(st)的接受狀態,N(s)的接受狀態和N(t)開始狀態成為一個狀態。這里提醒一下,寫程序的時候,這里千萬要注意,因為沒有新的狀態產生,必須考慮狀態的部分復制,如果不小心就會出錯。
c) 對于正規式 s*,構造N(s*)
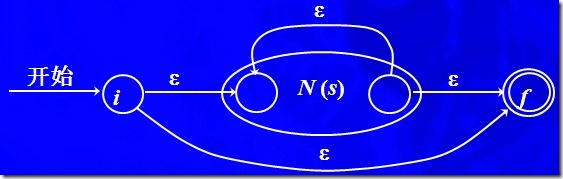
這里一樣需要產生2個新的狀態i,f,注意,產生了一條N(s)接受狀態到N(s)開始狀態的邊,邊上的symbol為 ε
d) 對于(s),使用N(s)本身作為它的NFA,也就是不用構造新的NFA
注意一下,以上產生的NFA,有以下性質:
1) 只有一個接受狀態和一個開始狀態
2) 每個狀態最多含有2個指向其他狀態的邊,詳細的來說,如果狀態只有一條指向其他狀態的邊,那么邊上的symbol為Σ中的任意字符或者ε,如果狀態有兩條指向其他狀態的邊,那么邊上的symbol一定為2個ε
由以上性質,我們可以很好的選擇數據結構來表示NFA
詞法分析(6)---DFA的化簡
通過NFA轉化而成的DFA不一定是最簡的,也就是說,有多余的狀態可以被刪除,對于每一個正規定義,我們一定可以得到一個唯一的最簡的DFA
我們回顧一下Move函數,DFA的move函數:
move : (state, symbol) -> S
注意,這里(state, symbol)表示的是一個集合,這里規范的數學表達應該是:
move : { (state, symbol) | 所有屬于DFA的state和symbol } -> S 或者
move : S × Σ -> S
假如一個DFA的move函數不是全函數,那么必須引入死狀態。假如某個DFA的move函數是全函數,那么每個狀態在所有input symbol下都有出邊,比如:
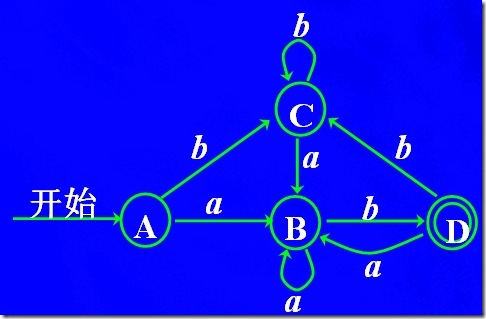
這個DFA每個狀態都可以接受所有的input symbol,這里是a,b。而下面的DFA:
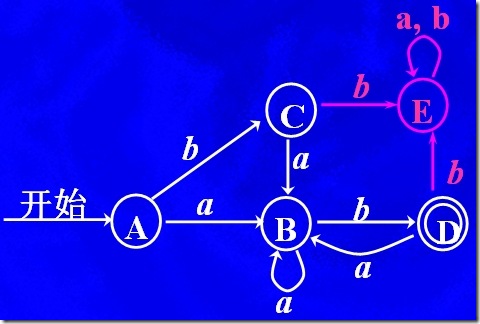
先不要看紅色部分,那么這個DFA的狀態c,d,它們無法通過input symbol b 進入下一個狀態,我們可以加上紅色的部分,把這個move函數,轉化成為一個全函數,并且,經過轉化操作之后,新的DFA與原DFA等價。這個紅色部分標識的狀態,被叫做死狀態
死狀態:
假如出現DFA的move函數不是全函數,我們可以引入一個死狀態S(僅僅引入一個方可),這個狀態包括所有input symbol對自身的轉換,所有的其他狀態假如不接受某個input symbol a,那么,我們建立這個狀態到S且input symbol為 a 的邊。
狀態的區別:
假如一個狀態s,通過input string w,可以轉換到某個狀態,而某個狀態t,通過w,轉化到了一個與s通過w轉化到的狀態不同的狀態,那么我們就可以通過w來區別狀態s,t,如果這樣的w不存在,那么s,t這2個狀態是無法區別的。
每個接受狀態都可以通過ε和非接受狀態進行區別。
化簡算法,極小化DFA的思想:
極小化DFA算法,它把狀態分成一些不相交的子集,每一個子集中的所有狀態都是不可區別的,而不同子集中的每個狀態兩兩都是可區別的,最后我們把每個子集中的所有狀態合成一個狀態。
1) 劃分狀態集
首先把所有狀態劃分成為2個集合,一個集合是接受狀態的集合,一個集合是非接受狀態的集合,他們通過ε來區別。然后看每個集合中的狀態時候還可以區別,例如一個集合通過input symbol a,轉換后得到的狀態落入當前劃分的不同集合,那么說明通過input symbol a,是可以區別這個集合中的狀態的(這里要強調的是,對于一個而不是多個input symbol,假如轉換到的狀態落入不同的劃分中那么這些狀態就是可以區別的)。我們假定有一個狀態集合{s1,s2},s1通過a到達狀態集合t1,s2通過a到達狀態集合t2,t1,t2分別是當前劃分的狀態集合,那么,集合{s1,s2}就可以分成2個集合{s1},{s2}
2) 構造最簡的DFA
我們可以重復1)的步驟,最后得到一些子集合,我們從每個子集合中取一個狀態,通過它們可以得到最簡的DFA,但具體需要按一定規則去構建
極小化DFA狀態數的算法:
Input : 一個DFA M,它的狀態集是S,輸入符號集合Σ,move : S × Σ -> S,開始狀態為s0,接受狀態的集合為F
Output : 一個DFA N,它和DFA M等價,并為最簡
Method :
1) 初始化: 假如move函數不是全函數,那么加入死狀態,構造劃分X:把S分成2個子集合,包括接受狀態集合F和非接受狀態集合S-F(F集合的補集)
2) Xnew是一個劃分
for( X 中的每個集合G ){
G中狀態每次通過Σ中的symbol轉化到的狀態如果屬于X的不同子集,那么把集合G分成子集,每個symbol都可能劃分G,劃分之后,使用下一個symbol進行操作,一直到遍歷完所有的input symbol
更新Xnew,用G的劃分代替G
}
3) 如果Xnew == X,那么定義 Xfinal = X,執行4),否則進行賦值操作 X = Xnew,進行2)
4) Xfinal中每個子集合中選擇一個狀態來代表這個狀態集合,包含s0的狀態集合,就是表示開始狀態的集合。通過DFA M來構造DFA N,規則是這樣的:假如某狀態p通過某input symbol a,通過DFA M的move函數轉到另外一個狀態q,我們就用q所在的集合的代表狀態來表示q,并把這個轉換過程的邊,input symbol,集合的代表狀態,加入DFA N中。我們需要遍歷DFA M,然后按規則構建DFA N。化簡的DFA中,可能有多個接受狀態。
5) 如果N中有死狀態(終態不是死狀態),去掉它,有開始狀態無法到達的狀態,也去掉它。注意,在DFA N中有可能出現死狀態,也就是通過所有的input symbol都回到自己的狀態,前面說過,添加一個死狀態得到的新的DFA與原DFA等價,那么我們這里也自然可以刪除它。
在真正的實現上面算法的時候,是靈活的,因為出于時間復雜度的考慮,可能并不需要完全照搬上面的算法,把握主要的思想是很重要的。
1) 每個input symbol都可能劃分一次集合
2) 每個集合都中的狀態被看成是不可區別的,即使在計算過程中某些集合中的狀態是可以區別的
3) 一定要確保每個集合都無法在分