參考原文:
http://tech.idv2.com/2006/05/08/parse-regex-with-dfa/
程序編譯的第一個階段是詞法分析,即把字節流識別為記號(token)流,提供給下一步的語法分析過程。而識別記號的方法就是正則表達式的分析。本文介紹利用有限自動機分析表達式的方法。
· 概念
· 將正則表達式轉換為NFA(Thompson構造法)
o 算法
o 性質
o 示例
· 將NFA轉化為DFA
o 算法
o 示例
· NFA和DFA的效率
概念
記號
有字母表中的符號組成的有限長度的序列。記號s的長度記為|s|。長度為0的記號稱為空記號,記為ε。
有限自動機(Finite State Automaton)
為研究某種計算過程而抽象出的計算模型。擁有有限個狀態,根據不同的輸入每個狀態可以遷移到其他的狀態。
非確定有限自動機(Nondeterministic Finite Automaton)
簡稱NFA,由以下元素組成:
1. 有限狀態集合S;
2. 有限輸入符號的字母表Σ;
3. 狀態轉移函數move;
4. 開始狀態 sSUB{0};
5. 結束狀態集合F,F ∈ S。
自動機初始狀態為sSUB{0},逐一讀入輸入字符串中的每一個字母,根據當前狀態、讀入的字母,由狀態轉移函數move控制進入下一個狀態。如果輸入字符串讀入結束時自動機的狀態屬于結束狀態集合F,則說明該自動機接受該字符串,否則為不接受。
確定有限自動機(Deterministic Finite Automaton)
簡稱DFA,是NFA的一種特例,有以下兩條限制:
1. 對于空輸入ε,狀態不發生遷移;
2. 某個狀態對于每一種輸入最多只有一種狀態轉移。
將正則表達式轉換為NFA(Thompson構造法)
算法
算法1 將正則表達式轉換為NFA(Thompson構造法)
輸入 字母表Σ上的正則表達式r
輸出 能夠接受L(r)的NFA N
方法 首先將構成r的各個元素分解,對于每一個元素,按照下述規則1和規則2生成NFA。 注意:如果r中記號a出現了多次,那么對于a的每次出現都需要生成一個單獨的NFA。
之后依照正規表達式r的文法規則,將生成的NFA按照下述規則3組合在一起。
規則1 對于空記號ε,生成下面的NFA。
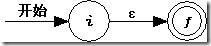
規則2 對于Σ的字母表中的元素a,生成下面的NFA。
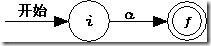
規則3 令正規表達式s和t的NFA分別為N(s)和N(t)。
a) 對于s|t,按照以下的方式生成NFA N(s|t)。
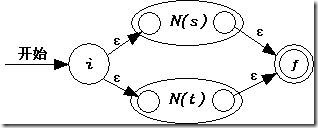
b) 對于st,按照以下的方式生成NFA N(st)。

c) 對于s*,按照以下的方式生成NFA N(s*)。
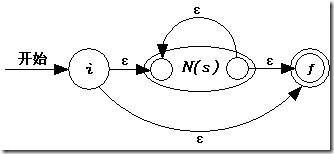
d) 對于(s),使用s本身的NFA N(s)。
性質
算法1生成的NFA能夠正確地識別正則表達式,并且具有如下的性質:
1. N(r)的狀態數最多為r中出現的記號和運算符的個數的2倍。
2. N(r)的開始狀態和結束狀態有且只有一個。
3. N(r)的各個狀態對于Σ中的一個符號,或者擁有一個狀態遷移,或者擁有最多兩個ε遷移。
示例
利用算法1,根據正則表達式 r=(a|b)*abb 可以生成以下的NFA。
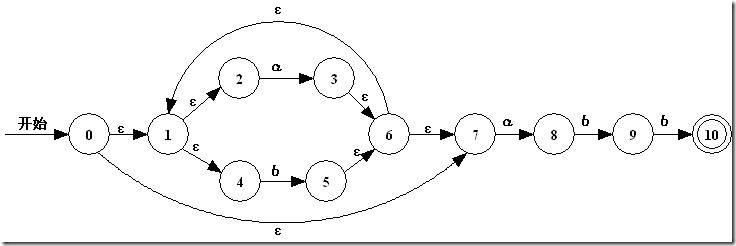
將NFA轉化為DFA
算法
使用以下的算法可以將NFA轉換成等價的DFA。
算法2 將NFA轉化為DFA
輸入 NFA N
輸出 能夠接受與N相同語言的DFA D
方法 本算法生成D對應的狀態遷移表Dtran。DFA的各個狀態為NFA的狀態集合,對于每一個輸入符號,D模擬N中可能的狀態遷移。
定義以下的操作。
| 操作 | 說明 |
| ε-closure(s) | 從NFA的狀態s出發,僅通過ε遷移能夠到達的NFA的狀態集合 |
| ε-closure(T) | 從T中包含的某個NFA的狀態s出發,僅通過ε遷移能夠到達的NFA的狀態集合 |
| move(T, a) | 從T中包含的某個NFA的狀態s出發,通過輸入符號a遷移能夠到達的NFA的狀態集合 |
令 Dstates 中僅包含ε-closure(s), 并設置狀態為未標記;
while Dstates中包含未標記的狀態T do
begin
標記T;
for 各輸入記號a do
begin
U := ε-closure(move(T, a));
if U不在Dstates中 then
將 U 追加到 Dstates 中,設置狀態為未標記;
Dtrans[T, a] := U;
end
end
ε-closure(T)的計算方法如下:
將T中的所有狀態入棧;
設置ε-closure(T)的初始值為T;
while 棧非空 do
begin
從棧頂取出元素t;
for 從t出發以ε為邊能夠到達的各個狀態u do
if u不在ε-closure(T)中 then
begin
將u追加到ε-closure(T)中;
將u入棧;
end
end
示例
將上面生成的NFA轉化為DFA。
最初,Dstates內僅有ε-closure(0) = A = {0, 1, 2, 4, 7}。然后對于狀態A,對于輸入記號a,計算 ε-closure(move(A, a)) = ε-closure(move({0, 1, 2, 4, 7}, a)) = ε-closure({3, 8}) = {1, 2, 3, 4, 6, 7, 8},即 B={1, 2, 3, 4, 6, 7, 8}, Dtran[A, a]=B。對于狀態A,由輸入記號b能夠到達的僅有4->5,因此 C = ε-closure({5}) = {1, 2, 4, 5, 6, 7},即 Dtran[A, b] = C。
以此類推,可得到以下的狀態和Dtran。
A = {0, 1, 2, 4, 7} D = {1, 2, 4, 5, 6, 7, 9}
B = {1, 2, 3, 4, 6, 7, 8} E = {1, 2, 4, 5, 6, 7, 10}
C = {1, 2, 4, 5, 6, 7}
| 狀態 | 輸入符號 |
| a | b |
| A | B | C |
| B | B | D |
| C | B | C |
| D | B | E |
| E | B | C |
由此得出DFA如下圖所示。
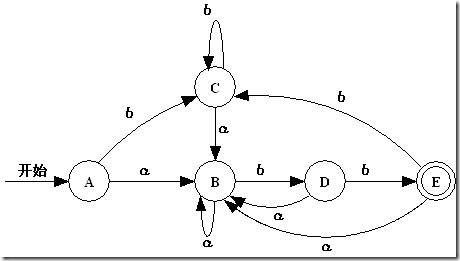
NFA和DFA的效率
給定正則表達式r和輸入記號序列x,判斷r是否能夠接受x。
使用NFA的情況下,由正則表達式生成NFA的時間復雜度為O(|r|),另外由于NFA的狀態數最多為r的2倍,因此空間復雜度為O(|r|)。由NFA判斷是否接受x時,時間復雜度為O(|r|×|x|)。因此,總體上處理時間與 r、x的長度之積成比例。這種處理方法在x不是很長時十分有效。
如果使用DFA,由于利用DFA判斷是否接受x與狀態數無關,因此時間復雜度為O(|x|)。但是DFA的狀態數與正則表達式的長度呈指數關系。例如,正規表達式 (a|b)*a(a|b)(a|b)...(a|b),尾部有 n-1 個 (a-b)的話, DFA最小狀態數也會超過 2SUP{n}。