| 一、深度優先搜索
深度優先搜索就是在搜索樹的每一層始終先只擴展一個子節點,不斷地向縱深前進直到不能再前進(到達葉子節點或受到深度限制)時,才從當前節點返回到上一級節點,沿另一方向又繼續前進。這種方法的搜索樹是從樹根開始一枝一枝逐漸形成的。
深度優先搜索亦稱為縱向搜索。由于一個有解的問題樹可能含有無窮分枝,深度優先搜索如果誤入無窮分枝(即深度無限),則不可能找到目標節點。所以,深度優先搜索策略是不完備的。另外,應用此策略得到的解不一定是最佳解(最短路徑)。
二、 重排九宮問題游戲
在一個3乘3的九宮中有1-8的8個數及一個空格隨機擺放在其中的格子里。如下面左圖所示。現在要求實現這樣的問題:將該九宮調整為如下圖右圖所示的形式。調整規則是:每次只能將與空格(上,下或左,右)相臨的一個數字平移到空格中。試編程實現。
| 2 | 8 | 3 | | 1 | 2 | 3 |
-
| 1 | | 4 | | 8 | | 4 |
| 7 | 6 | 5 | | 7 | 6 | 5 |
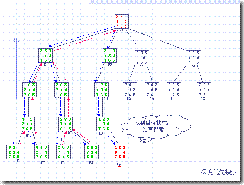
深度優先搜索的路徑示意圖:
|
| 
|
三、廣度優先搜索
在深度優先搜索算法中,是深度越大的結點越先得到擴展。如果在搜索中把算法改為按結點的層次進行搜索,本層的結點沒有搜索處理完時,不能對下層結點進行處理,即深度越小的結點越先得到擴展,也就是說先產生的結點先得以擴展處理,這種搜索算法稱為廣度優先搜索法。
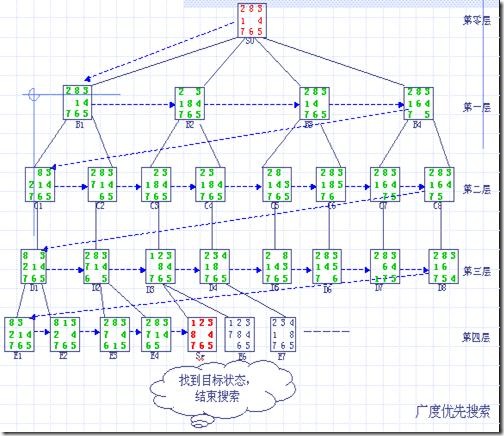
廣度優先搜索路徑示意圖:
四、航班問題(來自《The Art of Java》)
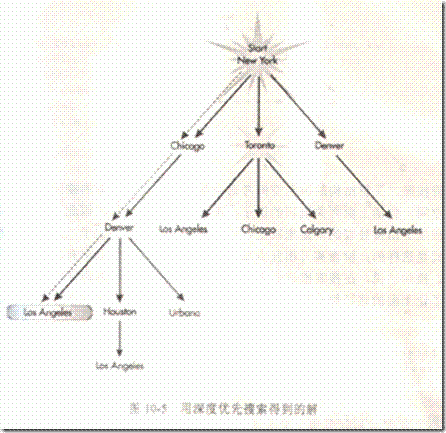
一位顧客要預定一張從New York到Los Angeles的航班機票,下面是航班線路,請你為顧客找一種購票方案。
| 航班 | 距離 |
| New York到Chicago | 900英里 |
| Chicago到Denver | 1000英里 |
| New York到Toronto | 500英里 |
| New York到Denver | 1800英里 |
| Toronto到Calgary | 1700英里 |
| Toronto到Los Angeles | 2500英里 |
| Toronto到Chicago | 500英里 |
| Denver到Urbana | 1000英里 |
| Denver到Houston | 1000英里 |
| Houston到Los Angeles | 1500英里 |
| Denver到Los Angeles | 1000英里 |
下面是用深度優先搜索求解的程序:
// Find connections using a depth-first search.
import java.util.*;
import java.io.*;
// Flight information.
class FlightInfo {
String from;
String to;
int distance;
boolean skip; // used in backtracking
FlightInfo(String f, String t, int d) {
from = f;
to = t;
distance = d;
skip = false;
}
}
class Depth {
final int MAX = 100;
// This array holds the flight information.
FlightInfo flights[] = new FlightInfo[MAX];
int numFlights = 0; // number of entries in flight array
Stack btStack = new Stack(); // backtrack stack
public static void main(String args[])
{
String to, from;
Depth ob = new Depth();
BufferedReader br = new
BufferedReader(new InputStreamReader(System.in));
ob.setup();
try {
System.out.print("From? ");
from = br.readLine();
System.out.print("To? ");
to = br.readLine();
ob.isflight(from, to);
if(ob.btStack.size() != 0)
ob.route(to);
} catch (IOException exc) {
System.out.println("Error on input.");
}
}
// Initialize the flight database.
void setup()
{
addFlight("New York", "Chicago", 900);
addFlight("Chicago", "Denver", 1000);
addFlight("New York", "Toronto", 500);
addFlight("New York", "Denver", 1800);
addFlight("Toronto", "Calgary", 1700);
addFlight("Toronto", "Los Angeles", 2500);
addFlight("Toronto", "Chicago", 500);
addFlight("Denver", "Urbana", 1000);
addFlight("Denver", "Houston", 1000);
addFlight("Houston", "Los Angeles", 1500);
addFlight("Denver", "Los Angeles", 1000);
}
// Put flights into the database.
void addFlight(String from, String to, int dist)
{
if(numFlights < MAX) {
flights[numFlights] =
new FlightInfo(from, to, dist);
numFlights++;
}
else System.out.println("Flight database full.\n");
}
// Show the route and total distance.
void route(String to)
{
Stack rev = new Stack();
int dist = 0;
FlightInfo f;
int num = btStack.size();
// Reverse the stack to display route.
for(int i=0; i < num; i++)
rev.push(btStack.pop());
for(int i=0; i < num; i++) {
f = (FlightInfo) rev.pop();
System.out.print(f.from + " to ");
dist += f.distance;
}
System.out.println(to);
System.out.println("Distance is " + dist);
}
/* If there is a flight between from and to,
return the distance of flight;
otherwise, return 0. */
int match(String from, String to)
{
for(int i=numFlights-1; i > -1; i--) {
if(flights[i].from.equals(from) &&
flights[i].to.equals(to) &&
!flights[i].skip)
{
flights[i].skip = true; // prevent reuse
return flights[i].distance;
}
}
return 0; // not found
}
// Given from, find any connection.
FlightInfo find(String from)
{
for(int i=0; i < numFlights; i++) {
if(flights[i].from.equals(from) &&
!flights[i].skip)
{
FlightInfo f = new FlightInfo(flights[i].from,
flights[i].to,
flights[i].distance);
flights[i].skip = true; // prevent reuse
return f;
}
}
return null;
}
// Determine if there is a route between from and to.
void isflight(String from, String to)
{
int dist;
FlightInfo f;
// See if at destination.
dist = match(from, to);
if(dist != 0) {
btStack.push(new FlightInfo(from, to, dist));
return;
}
// Try another connection.
f = find(from);
if(f != null) {
btStack.push(new FlightInfo(from, to, f.distance));
isflight(f.to, to);
}
else if(btStack.size() > 0) {
// Backtrack and try another connection.
f = (FlightInfo) btStack.pop();
isflight(f.from, f.to);
}
}
}
解釋:isflight()方法用遞歸方法進行深度優先搜索,它先調用match()方法檢查航班的數據庫,判斷在from和to之間有沒有航班可達。如果有,則獲取目標信息,并將該線路壓入棧中,然后返回(找到一個方案)。否則,就調用find()方法查找from與任意其它城市之間的線路,如果找到一條就返回描述該線路的FlightInfo對象,否則返回null。如果存在這樣的一條線路,那么就把該線路保存在f中,并將當前航班信息壓到棧的頂部,然后遞歸調用isflight()方法 ,此時保存在f.to中的城市成為新的出發城市.否則就進行回退,彈出棧頂的第一個節點,然后遞歸調用isflight()方法。該過程將一直持續到找到目標為止。
程序運行結果:
C:\java>java Depth
From? New York
To? Los Angeles
New York to Chicago to Denver to Los Angeles
Distance is 2900
C:\java>
深度優先搜索能夠找到一個解,同時,對于上面這個特定問題,深度優先搜索沒有經過回退,一次就找到了一個解;但如果數據的組織方式不同,尋找解時就有可能進行多次回退。因此這個例子的輸出并不具有普遍性。而且,在搜索一個很長,但是其中并沒有解的分支的時候,深度優先搜索的性能將會很差,在這種情況下,深度優先搜索不僅在搜索這條路徑時浪費時間,而且還在向目標的回退中浪費時間。
再看對這個例子使用廣度優先搜索的程序:
// Find connections using a breadth-first search.
import java.util.*;
import java.io.*;
// Flight information.
class FlightInfo {
String from;
String to;
int distance;
boolean skip; // used in backtracking
FlightInfo(String f, String t, int d) {
from = f;
to = t;
distance = d;
skip = false;
}
}
class Breadth {
final int MAX = 100;
// This array holds the flight information.
FlightInfo flights[] = new FlightInfo[MAX];
int numFlights = 0; // number of entries in flight array
Stack btStack = new Stack(); // backtrack stack
public static void main(String args[])
{
String to, from;
Breadth ob = new Breadth();
BufferedReader br = new
BufferedReader(new InputStreamReader(System.in));
ob.setup();
try {
System.out.print("From? ");
from = br.readLine();
System.out.print("To? ");
to = br.readLine();
ob.isflight(from, to);
if(ob.btStack.size() != 0)
ob.route(to);
} catch (IOException exc) {
System.out.println("Error on input.");
}
}
// Initialize the flight database.
void setup()
{
addFlight("New York", "Chicago", 900);
addFlight("Chicago", "Denver", 1000);
addFlight("New York", "Toronto", 500);
addFlight("New York", "Denver", 1800);
addFlight("Toronto", "Calgary", 1700);
addFlight("Toronto", "Los Angeles", 2500);
addFlight("Toronto", "Chicago", 500);
addFlight("Denver", "Urbana", 1000);
addFlight("Denver", "Houston", 1000);
addFlight("Houston", "Los Angeles", 1500);
addFlight("Denver", "Los Angeles", 1000);
}
// Put flights into the database.
void addFlight(String from, String to, int dist)
{
if(numFlights < MAX) {
flights[numFlights] =
new FlightInfo(from, to, dist);
numFlights++;
}
else System.out.println("Flight database full.\n");
}
// Show the route and total distance.
void route(String to)
{
Stack rev = new Stack();
int dist = 0;
FlightInfo f;
int num = btStack.size();
// Reverse the stack to display route.
for(int i=0; i < num; i++)
rev.push(btStack.pop());
for(int i=0; i < num; i++) {
f = (FlightInfo) rev.pop();
System.out.print(f.from + " to ");
dist += f.distance;
}
System.out.println(to);
System.out.println("Distance is " + dist);
}
/* If there is a flight between from and to,
return the distance of flight;
otherwise, return 0. */
int match(String from, String to)
{
for(int i=numFlights-1; i > -1; i--) {
if(flights[i].from.equals(from) &&
flights[i].to.equals(to) &&
!flights[i].skip)
{
flights[i].skip = true; // prevent reuse
return flights[i].distance;
}
}
return 0; // not found
}
// Given from, find any connection.
FlightInfo find(String from)
{
for(int i=0; i < numFlights; i++) {
if(flights[i].from.equals(from) &&
!flights[i].skip)
{
FlightInfo f = new FlightInfo(flights[i].from,
flights[i].to,
flights[i].distance);
flights[i].skip = true; // prevent reuse
return f;
}
}
return null;
}
/* Determine if there is a route between from and to
using breadth-first search. */
void isflight(String from, String to)
{
int dist, dist2;
FlightInfo f;
// This stack is needed by the breadth-first search.
Stack resetStck = new Stack();
// See if at destination.
dist = match(from, to);
if(dist != 0) {
btStack.push(new FlightInfo(from, to, dist));
return;
}
/* Following is the first part of the breadth-first
modification. It checks all connecting flights
from a specified node. */
while((f = find(from)) != null) {
resetStck.push(f);
if((dist = match(f.to, to)) != 0) {
resetStck.push(f.to);
btStack.push(new FlightInfo(from, f.to, f.distance));
btStack.push(new FlightInfo(f.to, to, dist));
return;
}
}
/* The following code resets the skip fields set by
preceding while loop. This is also part of the
breadth-first modifiction. */
int i = resetStck.size();
for(; i!=0; i--)
resetSkip((FlightInfo) resetStck.pop());
// Try another connection.
f = find(from);
if(f != null) {
btStack.push(new FlightInfo(from, to, f.distance));
isflight(f.to, to);
}
else if(btStack.size() > 0) {
// Backtrack and try another connection.
f = (FlightInfo) btStack.pop();
isflight(f.from, f.to);
}
}
// Reset skip field of specified flight.
void resetSkip(FlightInfo f) {
for(int i=0; i< numFlights; i++)
if(flights[i].from.equals(f.from) &&
flights[i].to.equals(f.to))
flights[i].skip = false;
}
}
程序運行結果:
C:\java>java Breadth
From? New York
To? Los Angeles
New York to Toronto to Los Angeles
Distance is 3000
C:\java>
它找到了一個合理的解,但這不具有一般性。因為找到的第一條路徑取決于信息的物理組織形式。

如果目標在搜索空間中隱藏得不是太深,那么廣度優先搜索的性能會很好。