基本描述
自動機是有限狀態(tài)機(FSM)的數(shù)學模型。FSM 是給定符號輸入，依據(jù)(可表達為一個表格的)轉移函數(shù)“跳轉”過一系列狀態(tài)的一種機器。在常見的 FSM 的“Mealy”變體中，這個轉移函數(shù)告訴自動機給定當前狀態(tài)和當前字符的時候下一個狀態(tài)是什么。
逐個讀取輸入中的符號，直到被完全耗盡(把它當作有一個字寫在其上的磁帶，通過自動機的讀磁頭來讀取它；磁頭在磁帶上前行移動，一次讀一個符號)。一旦輸入被耗盡，自動機被稱為“停止”了。
依賴自動機停止時的狀態(tài)，稱呼這個自動機要么是“接受”要么“拒絕”這個輸入。如果停止于“接受狀態(tài)”，則自動機“接受”了這個字。在另一方面，如果它停止于“拒絕狀態(tài)”，則這個字被“拒絕”。自動機接受的所有字的集合被稱為“這個自動機接受的語言”。
但要注意，自動機一般不必須有有限數(shù)目甚至可數(shù)個狀態(tài)。比如，量子有限自動機有不可數(shù)無限個狀態(tài)，因為所有可能狀態(tài)的集合是在復投影空間中所有點的集合。所以，量子有限自動機和有限狀態(tài)機一樣，都是更一般想法拓撲自動機的特殊情況，它的狀態(tài)的集合是拓撲空間，而狀態(tài)轉移函數(shù)取自在這個空間上的所有可能函數(shù)。拓撲自動機經常叫做 M-自動機，簡單是半自動機加上接受狀態(tài)集合的補充，這里的集合交集確定初始狀態(tài)是被接受還是被拒絕。
一般的說，自動機不需要嚴格的接受或拒絕一個輸入；它可以按某個在零和一之間的概率接受它。還是用量子有限自動機作為展示例子，它只按某個概率接受輸入。這個想法也是更一般情況幾何自動機或度量自動機的特殊情況，它的狀態(tài)的集合是度量空間，一個語言被這個自動機接受如果在初始點和接受狀態(tài)的集合之間的距離關于這個度量是足夠的小。
[編輯] 術語
自動機有如下基本概念：
符號
有某種意義或在這個機器上有效的任意數(shù)據(jù)(datum)。符號有時就叫做“字母”。
字
通過一些符號串接而形成的有限字符串。
字母表
符號的有限集合。字母表經常指示為 Σ，它是在字母表中所有字母的集合。
語言
字的集合，由給頂字母表中的符號形成。可以是也可以不是無限的。
Kleene閉包
一個語言可以被認為是所有可能字的子集。所有可能字的集合可以被認為是所有可能的字符串串接的集合。形式上說，所有可能字符串的集合叫做自由幺半群。它被指示為 Σ * ，上標 * 被稱為 Kleene星號。
[編輯] 形式描述
自動機可以表示為5-元組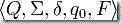 
，這里的:
- Q 是狀態(tài)的集合。
- ∑ 是符號的有限集合，我們稱為這個自動機接受的語言的字母表。
- δ 是轉移函數(shù)，就是
。
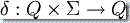(對于非確定自動機，空串是允許的輸入)。
- q0 是開始狀態(tài)，就是說自動機在還未處理輸入的時候的狀態(tài)(明顯的 q0∈ Q)。
- F 是叫做接受狀態(tài)的 Q 中的狀態(tài)的集合(就是 F?Q)。
給定一個輸入字母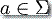 
，可以使用簡單的 currying 技巧寫轉移函數(shù)為 
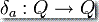，就是說，寫 δ(q,a) = δa(q) 對于所有
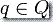。這種方式下轉移可以被更簡單的看待: 它就是“動作”于 Q 中一個狀態(tài)上的生成另一個狀態(tài)的某種東西。你可以接著考慮重復的應用函數(shù)復合于各種函數(shù) δa, δb 等等的結果。重復的函數(shù)復合形成一個幺半群。對于轉移函數(shù)，這個幺半群叫做轉移幺半群，有時也叫做“變換半群”。
給定一對字母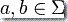 
，可以通過堅持 
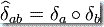定義一個新函數(shù) 
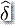，這里的 
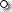指示函數(shù)復合。明顯的，可以遞歸的繼續(xù)這個過程，這樣就有了為所有字 
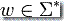定義的函數(shù) 
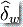的遞歸定義，因此有了映射
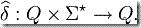
這個構造也可以反過來: 給定 
，可以重新構造一個 δ，因此兩個描述是等價的。
三元組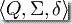 
被稱為半自動機。半自動機位于自動機底下，它們就是忽略了開始狀態(tài)和接受狀態(tài)的自動機。開始狀態(tài)和接受狀態(tài)的補充概念允許自動機做半自動機不能做的事情: 它們可以識別形式語言。確定有限自動機 
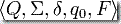接受的語言 L 是:
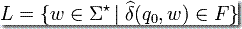
就是說，一個自動機所接受的語言是在字母表 Σ 之上所有字 w 的集合，當給定為自動機的輸入的時候，將導致它停止于 F 中的某個狀態(tài)。被自動機接受的語言叫做可識別語言。
當狀態(tài)集合 Q 是有限的時候，自動機被稱為有限狀態(tài)自動機，而所有可識別的語言是正則語言。事實上，有一個強等價: 對于所有正則語言，都有一個有限狀態(tài)自動機，反之亦然。
如上所述，集合 Q 不必須是有限或可數(shù)的；它可以采用一般的拓撲空間；這就得到了一般的拓撲自動機。另一種可能的推廣是度量自動機或“幾何自動機”。在這種情況下，改變了對語言的接受: 替代在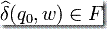 
中的最終狀態(tài)的集合包含，以在最終狀態(tài) 
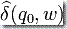和集合 F 之間的度量距離的方式給出。特定類型的概率自動機是度量自動機，其度量空間是在概率空間上的測量。
[編輯] 有限自動機的分類
下面是三類有限自動機
確定有限自動機(DFA)
對字母表中每個符號，自動機的狀態(tài)都有且僅有一個轉移。
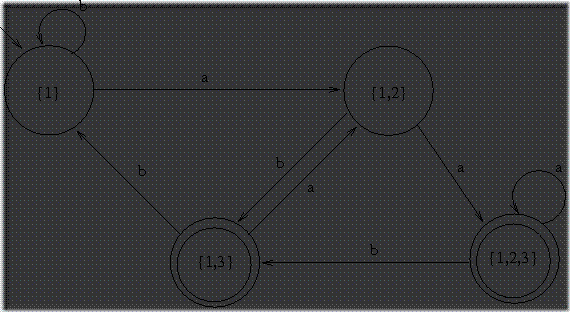
DFA
非確定有限自動機(NFA)
自動機的狀態(tài)對字母表中的每個符號可以有也可以沒有轉移，對一個符號甚至可以有多個轉移。自動機接受一個字，如果存在至少一個從 q0 到 F 中標記(label)著這個輸入字的一個狀態(tài)的路徑。如果一個轉移是“未定義”的，自動機因此不知道如何繼續(xù)讀取輸入，則拒絕這個字。
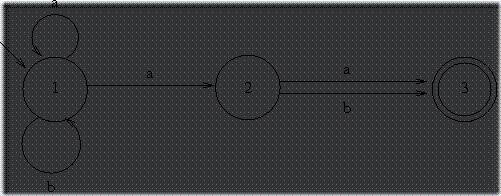
等價于前面例子 DFA 的 NFA
有ε轉移的非確定有限自動機(FND-ε或ε-NFA)
除了有能力對任何符號跳轉到更多狀態(tài)或沒有狀態(tài)可以跳轉之外，它們可以做根本不關于符號的跳轉。就是說，如果一個狀態(tài)有標記著 ε 的轉移，則 NFA 可以處在 ε-轉移可到達的任何狀態(tài)中，直接或通過其他有 ε-轉移的狀態(tài)。從一個狀態(tài) q 通過這種方法可到達的狀態(tài)的集合叫做 q 的 ε-閉包。
盡管可以證明所有這些自動機都“可以接受同樣的語言”。你總是可以構造接受與給定的 NFA M 同樣語言的某個 DFA M。
[編輯] 有限自動機的擴展
上述自動機接受的語言家族被稱為正則語言家族。更強力的自動機可以接受更復雜的語言。比如:
下推自動機(PDA)
這種機器等同于 DFA (或 NFA)，除了它們額外的裝備了棧形式的內存。轉移函數(shù) δ 也依賴于在棧頂?shù)姆枺⒃诿看无D移時指定如何變更棧。非確定 PDA 接受上下文無關語言。
線性有界自動機(LBA)
LBA 是有限制的圖靈機；不使用無限磁帶，它的磁帶有同輸入字符串成正比的空間。LBA 接受上下文有關語言。
圖靈機
它們是最強力的計算機器。它們擁有磁帶形式的無限內存，和可以讀取和變更磁帶的磁頭，它可在磁帶上向任何方向移動。圖靈機等價于算法，是現(xiàn)代計算機的理論基礎。圖靈機判定遞歸語言并識別遞歸可枚舉語言。
[編輯] 有限狀態(tài)自動機的最小化
根據(jù) Myhill-Nerode定理，在同構意義下接受一個正則語言的最少狀態(tài)的確定有限狀態(tài)自動機是唯一的。同時我們還存在有效的算法（時間開銷是O(n2)的）構造出與給定確定有限狀態(tài)自動機等價的最小化的確定有限狀態(tài)自動機。
[編輯] 計算能力與判定問題
確定有限狀態(tài)自動機與非確定有限狀態(tài)自動機識別的語言都是正則語言。由于正則語言的良好性質，許多為其他自動機（下推自動機或圖靈機）不能判定的問題，在有限狀態(tài)自動機的情形下，都可以得到判定，并且存在有效的算法。
對一個確定有限狀態(tài)自動機，下述判定問題都可以判定，并且存在有效的算法。
- 該自動機識別的語言是否為空集。
- 該自動機識別的語言是否為有限集。
- 該自動機是否與另一個確定有限狀態(tài)自動機識別同一個的語言。
[編輯] 外部鏈接
[編輯] 引用
- John E. Hopcroft, Rajeev Motwani, Jeffrey D. Ullman - Introduction to Automata Theory, Languages, and Computation (2nd Edition)
- Michael Sipser（1997）．Introduction to the Theory of Computation．PWS Publishing．ISBN 0-534-94728-X． Part One: Automata and Languages, chapters 1–2, pp.29–122. Section 4.1: Decidable Languages, pp.152–159. Section 5.1: Undecidable Problems from Language Theory, pp.172–183.
取自"