一個非確定自動機( NFA) 在讀入符號串之后,并不確切地知道自動機處于哪個狀態。但可以肯定一定處于狀態集中的某一狀態。該狀態集記做 {q1,q2,…qk} 。而一個等價的確定自動機( DFA) 讀入同樣的 w 一定處于某個確定的狀態上。這樣,都是讀入同樣的 w , DFA 到達某一個狀態,而 NFA 到達某一個狀態集。由 w 的任意性,可將 NFA 的所有的狀態集和 DFA 的狀態一一對應起來。這種對應的前提就是能識別同樣的輸入串。即 L(M1)=L(M2) 。
顯然,后一個狀態集是依賴于前一個狀態集的,是在前一個狀態集的基礎上,(其內任意結點)經過同一條路徑到達的。下面是一個簡單的例子:
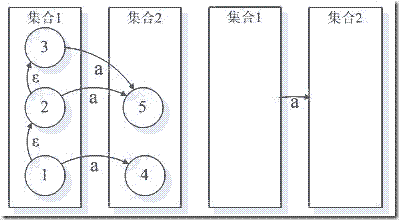
可以看出,其核心是將 NFA 狀態集歸并為 DFA 中的狀態。在 NFA 中,無論是從 1 到 4 ,還是 1 到 5 ,作為集合來講都是集合 1 到集合 2 ,最為重要得是經過的條件都是 a 。因而從識別語言的效果是一樣的。這使得這些弧合并成為可能。
考慮集合覆蓋的情況。
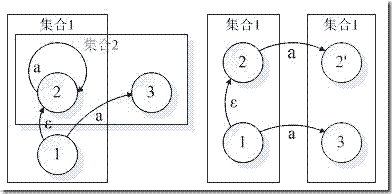
一個結點屬于第一個集合又同時屬于第二個集合。這種情況不一定好理解。但如果從路徑的歷史的角度進一步區分,即不同的時間經過同一個結點,將其看成是不同的狀態。按照這種時空的角度進一步區分,得到右圖。這和圖 1 是類似的。
再來看看帶有終態結點的情況:
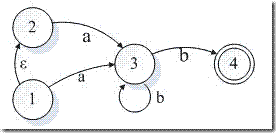
ab , abb 均為該 NFA 識別的句子,其轉換如下:
| | I a | Ib |
| A{1,2} | {3} | Φ |
| B{3} | Φ | {3,4} |
| C{3,4} | Φ | {3,4} |
從某種意義上說。 NFA 中的狀態 3 在 DFA 中被分離成兩部分,當首次到達 3 時應該是狀態 B ,而第二次以后再到達 3 則應該屬于狀態 C 。
根據規則, C{3,4} 為 DFA 的終態,但在 NFA 中,只有 4 為終態, C 中仍然有 3 為非終態,若有路徑 1 à 3 à 3 映射到 DFA 中也是 A à B à C ,何解?
這里面最關鍵的是:對任意一個句子,總可以在兩個圖中分別找到一條路徑,形成對應關系。并不是說 NFA 中的每條路徑都要和 DFA 中的每條路徑一一對應。
當識別句子 ab 時,選擇由 3 直接到達 4 的路徑。當識別句子 abb 時,則在狀態 3 循環一次再到達 4 。
現在設想,通過 1 à 3 à 3 經過的路徑也是 ab 。但此時并未到達終態。可以說,在到達 C 中的 3 時,必然選擇了兩個 b 以上的句子。
而這樣的路徑與選擇句子有關系。
對于 NFA 能識別的句子,在 DFA 中也能識別。
對于 NFA 不能識別的句子,在 DFA 中也不能識別。