一、概述Strategy(策略)模式又稱Policy模式,用于定義一系列的算法,把它們一個(gè)個(gè)封裝起來,并且使它們可相互替換。這里的算法并非狹義的數(shù)據(jù)結(jié)構(gòu)或算法理論中所討論的KMP、shell sort等算法,而是指應(yīng)用程序設(shè)計(jì)中不同的處理邏輯,前面所說的狹義的算法只是其中的一部分。Strategy模式使得算法與算法的使用者相分離,減少了二者間的耦合度,使得算法可獨(dú)立于使用它的客戶而變化;同時(shí),由于設(shè)計(jì)粒度的減小,程序的復(fù)用性也得到了進(jìn)一步提高,分離出來的算法可以更好地適應(yīng)復(fù)用的需要。二、結(jié)構(gòu)Strategy模式的結(jié)構(gòu)如下圖所示: 計(jì)模式/Strategy.jpg) 從結(jié)構(gòu)上看,Strategy模式與State模式有幾分相似,但二者所討論的Context(情景)具有顯著的差異:State模式在于將其狀態(tài)信息分離出來保存到一個(gè)獨(dú)立的對(duì)象中,以便狀態(tài)信息的獲取或狀態(tài)的轉(zhuǎn)換;Strategy模式在于將可能的算法分離出來,根據(jù)需要進(jìn)行適當(dāng)?shù)倪x擇。此外,二者的區(qū)別還在于,Strategy模式中各個(gè)Strategy(算法、策略)往往用于解決相同的問題,即只是解決同一問題的不同“策略”、“途徑”,而且,一次只能有一個(gè)Strategy為上次應(yīng)用提供服務(wù);而State模式中的各個(gè)State本身往往具有一定的差異,但他們之間存在明顯的相互轉(zhuǎn)換的關(guān)系,而且這種轉(zhuǎn)換往往會(huì)在程序運(yùn)行過程中經(jīng)常性地發(fā)生,同時(shí)存在一個(gè)以上State也是可能的。區(qū)別參考:二者的應(yīng)用場(chǎng)合不同。狀態(tài)模式用于處理對(duì)象有不同狀態(tài)(狀態(tài)機(jī))的場(chǎng)合,策略模式用于隨不同外部環(huán)境采取不同行為的場(chǎng)合。在狀態(tài)模式中,狀態(tài)的變遷是由對(duì)象的內(nèi)部條件決定,外界只需關(guān)心其接口,不必關(guān)心其狀態(tài)對(duì)象的創(chuàng)建和轉(zhuǎn)化;而策略模式里,采取何種策略由外部條件決定。所以,有人說“狀態(tài)模式是完全封裝且自修改的策略模式”。至于Bridge,在結(jié)構(gòu)上與前兩者都不一樣了。要說相似之處,就是三者都有具有對(duì)外接口統(tǒng)一的類,展現(xiàn)出多態(tài)性而已。三、應(yīng)用當(dāng)存在以下情況時(shí)可考慮使用Strategy模式:
從結(jié)構(gòu)上看,Strategy模式與State模式有幾分相似,但二者所討論的Context(情景)具有顯著的差異:State模式在于將其狀態(tài)信息分離出來保存到一個(gè)獨(dú)立的對(duì)象中,以便狀態(tài)信息的獲取或狀態(tài)的轉(zhuǎn)換;Strategy模式在于將可能的算法分離出來,根據(jù)需要進(jìn)行適當(dāng)?shù)倪x擇。此外,二者的區(qū)別還在于,Strategy模式中各個(gè)Strategy(算法、策略)往往用于解決相同的問題,即只是解決同一問題的不同“策略”、“途徑”,而且,一次只能有一個(gè)Strategy為上次應(yīng)用提供服務(wù);而State模式中的各個(gè)State本身往往具有一定的差異,但他們之間存在明顯的相互轉(zhuǎn)換的關(guān)系,而且這種轉(zhuǎn)換往往會(huì)在程序運(yùn)行過程中經(jīng)常性地發(fā)生,同時(shí)存在一個(gè)以上State也是可能的。區(qū)別參考:二者的應(yīng)用場(chǎng)合不同。狀態(tài)模式用于處理對(duì)象有不同狀態(tài)(狀態(tài)機(jī))的場(chǎng)合,策略模式用于隨不同外部環(huán)境采取不同行為的場(chǎng)合。在狀態(tài)模式中,狀態(tài)的變遷是由對(duì)象的內(nèi)部條件決定,外界只需關(guān)心其接口,不必關(guān)心其狀態(tài)對(duì)象的創(chuàng)建和轉(zhuǎn)化;而策略模式里,采取何種策略由外部條件決定。所以,有人說“狀態(tài)模式是完全封裝且自修改的策略模式”。至于Bridge,在結(jié)構(gòu)上與前兩者都不一樣了。要說相似之處,就是三者都有具有對(duì)外接口統(tǒng)一的類,展現(xiàn)出多態(tài)性而已。三、應(yīng)用當(dāng)存在以下情況時(shí)可考慮使用Strategy模式:
1.許多相關(guān)的類僅僅是行為有異。“策略”提供了一種用多個(gè)行為中的一個(gè)行為來配置一個(gè)類的方法。
2.需要使用一個(gè)算法的不同變體。例如,你可能會(huì)定義一些反映不同的空間/時(shí)間權(quán)衡的算法,當(dāng)這些變體實(shí)現(xiàn)為一個(gè)算法的類層次時(shí),可以使用策略模式。
3.算法使用客戶不應(yīng)該知道的數(shù)據(jù)。可使用策略模式以避免暴露復(fù)雜的、與算法相關(guān)的數(shù)據(jù)結(jié)構(gòu)。
4.一個(gè)類定義了多種行為,并且這些行為在這個(gè)類的操作中以多個(gè)條件語句的形式出現(xiàn)。將相關(guān)的條件分支移入它們各自的Strategy類中以代替這些條件語句。更具體的應(yīng)用實(shí)例包括:
1.以不同的格式保存文件;
2.以不同的方式對(duì)文件進(jìn)行壓縮或其他處理;
3.以不同的方式繪制/處理相同的圖形數(shù)據(jù);等等。四、舉例下面是一個(gè)應(yīng)用Strategy模式對(duì)vector進(jìn)行排序的例子,為了簡(jiǎn)化問題,其中的排序Strategy實(shí)際上調(diào)用的是STL的排序算法:sort和stable_sort。
1 #include <iostream>
2 #include <vector>
3 #include <algorithm>
4 #include <time.h>
5 using namespace std;
6
7 template <typename T>
8 class SortStrategy // Strategy
9 {
10 public:
11 virtual void Sort( vector<T>& v_t ) = 0;
12 };
13
14 template <typename T>
15 class SortQuick : public SortStrategy<T> // ConcreateStrategy1
16 {
17 public:
18 void Sort( vector<T>& v_t ) { std::sort( v_t.begin(), v_t.end() ); }
19 };
20
21 template <typename T>
22 class SortStable : public SortStrategy<T> // ConcreateStrategy1
23 {
24 public:
25 void Sort( vector<T>& v_t ) { std::stable_sort(v_t.begin(), v_t.end()); }
26 };
27
28 template <typename T>
29 class Context { // Context, who or whose client takes charge of which strategy will be selected
30 public:
31 Context() { m_pStrategy = NULL; }
32 virtual ~Context() { if (m_pStrategy != NULL) delete m_pStrategy; }
33
34 void SetStrategy(SortStrategy<T>* pStrategy); // select a strategy
35
36 void ReadVector( vector<T>& v_t);
37 bool SortVector();
38 void OutputVector();
39 private:
40 vector<T> m_vt;
41 SortStrategy<T>* m_pStrategy; // a pointer to current strategy
42 };
43
44 template <typename T>
45 void Context<T>::SetStrategy( SortStrategy<T>* pStrategy )
46 {
47 if ( NULL != m_pStrategy )
48 delete m_pStrategy;
49
50 m_pStrategy = pStrategy;
51 }
52
53 template <typename T>
54 void Context<T>::ReadVector( vector<T>& v_t)
55 {
56 m_vt.clear();
57 copy( v_t.begin(), v_t.end(), back_inserter( m_vt ) );
58 }
59
60 template <typename T>
61 bool Context<T>::SortVector()
62 {
63 if ( NULL == m_pStrategy )
64 return false;
65
66 m_pStrategy->Sort( m_vt );
67
68 return true;
69 }
70
71 template <typename T>
72 void Context<T>::OutputVector()
73 {
74 copy( m_vt.begin(), m_vt.end(), ostream_iterator<T>( cout, " " ) );
75 }
76
77 // a functor to generate random int
78 struct RandGen
79 {
80 RandGen(int ratio) { m_ratio = ratio; }
81 int operator() () { return rand() % m_ratio + 1; }
82 private:
83 int m_ratio;
84 };
85
86 int main()
87 {
88 const int NUM = 9;
89 vector< int > vi;
90 time_t t;
91 srand( (unsigned) time(&t) );
92
93 // create a vector with random information
94 vi.reserve(NUM + 1);
95 generate_n(back_inserter(vi), NUM, RandGen(NUM));
96
97 Context< int > con;
98 con.SetStrategy( new SortQuick<int>() );
99 con.ReadVector( vi );
100 con.OutputVector();
101
102 cout << endl;
103
104 con.SortVector();
105 con.OutputVector();
106
107 return 0;
108 }
本文轉(zhuǎn)自:http://blog.csdn.net/haiyan0106/article/details/1651797
一、概述
Iterator(迭代器)模式又稱Cursor(游標(biāo))模式,用于提供一種方法順序訪問一個(gè)聚合對(duì)象中各個(gè)元素, 而又不需暴露該對(duì)象的內(nèi)部表示。或者這樣說可能更容易理解:Iterator模式是運(yùn)用于聚合對(duì)象的一種模式,通過運(yùn)用該模式,使得我們可以在不知道對(duì)象內(nèi)部表示的情況下,按照一定順序(由iterator提供的方法)訪問聚合對(duì)象中的各個(gè)元素。
由于Iterator模式的以上特性:與聚合對(duì)象耦合,在一定程度上限制了它的廣泛運(yùn)用,一般僅用于底層聚合支持類,如STL的list、vector、stack等容器類及ostream_iterator等擴(kuò)展iterator。
根據(jù)STL中的分類,iterator包括:
Input Iterator:只能單步向前迭代元素,不允許修改由該類迭代器引用的元素。
Output Iterator:該類迭代器和Input Iterator極其相似,也只能單步向前迭代元素,不同的是該類迭代器對(duì)元素只有寫的權(quán)力。
Forward Iterator:該類迭代器可以在一個(gè)正確的區(qū)間中進(jìn)行讀寫操作,它擁有Input Iterator的所有特性,和Output Iterator的部分特性,以及單步向前迭代元素的能力。
Bidirectional Iterator:該類迭代器是在Forward Iterator的基礎(chǔ)上提供了單步向后迭代元素的能力。
Random Access Iterator:該類迭代器能完成上面所有迭代器的工作,它自己獨(dú)有的特性就是可以像指針那樣進(jìn)行算術(shù)計(jì)算,而不是僅僅只有單步向前或向后迭代。
這五類迭代器的從屬關(guān)系,如下圖所示,其中箭頭A→B表示,A是B的強(qiáng)化類型,這也說明了如果一個(gè)算法要求B,那么A也可以應(yīng)用于其中。
圖1、五種迭代器之間的關(guān)系
vector 和deque提供的是RandomAccessIterator,list提供的是BidirectionalIterator,set和map提供的 iterators是 ForwardIterator,關(guān)于STL中iterator的更多信息。
二、結(jié)構(gòu)
Iterator模式的UML結(jié)構(gòu)如下圖所示:
計(jì)模式/gof32.jpg)
三、應(yīng)用
Iterator模式有三個(gè)重要的作用:
1)它支持以不同的方式遍歷一個(gè)聚合 復(fù)雜的聚合可用多種方式進(jìn)行遍歷,如二叉樹的遍歷,可以采用前序、中序或后序遍歷。迭代器模式使得改變遍歷算法變得很容易: 僅需用一個(gè)不同的迭代器的實(shí)例代替原先的實(shí)例即可,你也可以自己定義迭代器的子類以支持新的遍歷,或者可以在遍歷中增加一些邏輯,如有條件的遍歷等。
2)迭代器簡(jiǎn)化了聚合的接口 有了迭代器的遍歷接口,聚合本身就不再需要類似的遍歷接口了,這樣就簡(jiǎn)化了聚合的接口。
3)在同一個(gè)聚合上可以有多個(gè)遍歷 每個(gè)迭代器保持它自己的遍歷狀態(tài),因此你可以同時(shí)進(jìn)行多個(gè)遍歷。
4)此外,Iterator模式可以為遍歷不同的聚合結(jié)構(gòu)(需擁有相同的基類)提供一個(gè)統(tǒng)一的接口,即支持多態(tài)迭代。
簡(jiǎn) 單說來,迭代器模式也是Delegate原則的一個(gè)應(yīng)用,它將對(duì)集合進(jìn)行遍歷的功能封裝成獨(dú)立的Iterator,不但簡(jiǎn)化了集合的接口,也使得修改、增 加遍歷方式變得簡(jiǎn)單。從這一點(diǎn)講,該模式與Bridge模式、Strategy模式有一定的相似性,但I(xiàn)terator模式所討論的問題與集合密切相關(guān), 造成在Iterator在實(shí)現(xiàn)上具有一定的特殊性,具體將在示例部分進(jìn)行討論。
四、優(yōu)缺點(diǎn)
正如前面所說,與集合密切相關(guān),限制了 Iterator模式的廣泛使用,就個(gè)人而言,我不大認(rèn)同將Iterator作為模式提出的觀點(diǎn),但它又確實(shí)符合模式“經(jīng)常出現(xiàn)的特定問題的解決方案”的 特質(zhì),以至于我又不得不承認(rèn)它是個(gè)模式。在一般的底層集合支持類中,我們往往不愿“避輕就重”將集合設(shè)計(jì)成集合 + Iterator 的形式,而是將遍歷的功能直接交由集合完成,以免犯了“過度設(shè)計(jì)”的詬病,但是,如果我們的集合類確實(shí)需要支持多種遍歷方式(僅此一點(diǎn)仍不一定需要考慮 Iterator模式,直接交由集合完成往往更方便),或者,為了與系統(tǒng)提供或使用的其它機(jī)制,如STL算法,保持一致時(shí),Iterator模式才值得考 慮。
五、舉例
可以考慮使用兩種方式來實(shí)現(xiàn)Iterator模式:內(nèi)嵌類或者友元類。通常迭代類需訪問集合類中的內(nèi)部數(shù)據(jù)結(jié)構(gòu),為此,可在集合類中設(shè)置迭代類為friend class,但這不利于添加新的迭代類,因?yàn)樾枰薷募项悾砑?font color="#990000">friend class語句。也可以在抽象迭代類中定義protected型的存取集合類內(nèi)部數(shù)據(jù)的函數(shù),這樣迭代子類就可以訪問集合類數(shù)據(jù)了,這種方式比較容易添加新的迭代方式,但這種方式也存在明顯的缺點(diǎn):這些函數(shù)只能用于特定聚合類,并且,不可避免造成代碼更加復(fù)雜。
STL的list::iterator、deque::iterator、rbtree::iterator等采用的都是外部Iterator類的形式,雖然STL的集合類的iterator分散在各個(gè)集合類中,但由于各Iterator類具有相同的基類,保持了相同的對(duì)外的接口(包括一些traits及tags等,感興趣者請(qǐng)認(rèn)真閱讀參考1、2),從而使得它們看起來仍然像一個(gè)整體,同時(shí)也使得應(yīng)用algorithm成為可能。我們?nèi)绻獢U(kuò)展STL的iterator,也需要注意這一點(diǎn),否則,我們擴(kuò)展的iterator將可能無法應(yīng)用于各algorithm。
以下是一個(gè)遍歷二叉樹的Iterator的例子,為了方便支持多種遍歷方式,并便于遍歷方式的擴(kuò)展,其中還使用了Strategy模式(見筆記21):
(注:1、雖然下面這個(gè)示例是本系列所有示例中花費(fèi)我時(shí)間最多的一個(gè),但我不得不承認(rèn),它非常不完善,感興趣的朋友,可以考慮參考下面的參考材料將其補(bǔ)充完善,或提出寶貴改進(jìn)意見。2、 我本想考慮將其封裝成與STL風(fēng)格一致的形式,使得我們遍歷二叉樹必須通過Iterator來進(jìn)行,但由于二叉樹在結(jié)構(gòu)上較線性存儲(chǔ)結(jié)構(gòu)復(fù)雜,使訪問必須 通過Iterator來進(jìn)行,但這不可避免使得BinaryTree的訪問變得異常麻煩,在具體應(yīng)用中還需要認(rèn)真考慮。3、以下只提供了Inorder<中序>遍歷iterator的實(shí)現(xiàn)。)
1 #include <assert.h>
2
3 #include <iostream>
4 #include <xutility>
5 #include <iterator>
6 #include <algorithm>
7 using namespace std;
8
9 template <typename T>
10 class BinaryTree;
11 template <typename T>
12 class Iterator;
13
14 template <typename T>
15 class BinaryTreeNode
16 {
17 public:
18 typedef BinaryTreeNode<T> NODE;
19 typedef BinaryTreeNode<T>* NODE_PTR;
20
21 BinaryTreeNode(const T& element) : data(element), leftChild(NULL), rightChild(NULL), parent(NULL) { }
22 BinaryTreeNode(const T& element, NODE_PTR leftChild, NODE_PTR rightChild)
23 :data(element), leftChild(leftChild), rightChild(rightChild), parent(NULL)
24 {
25 if (leftChild)
26 leftChild->setParent(this);
27 if (rightChild)
28 rightChild->setParent(this);
29 }
30
31 T getData(void) const { return data; }
32 NODE_PTR getLeft(void) const { return leftChild; }
33 NODE_PTR getRight(void) const { return rightChild; }
34 NODE_PTR getParent(void) const { return parent; }
35 void SetData(const T& data) { this->data = item; }
36 void setLeft(NODE_PTR ptr) { leftChild = ptr; ptr->setParent(this); }
37 void setRight(NODE_PTR ptr) { rightChild = ptr; ptr->setParent(this); }
38 void setParent(NODE_PTR ptr) { parent = ptr; }
39 private:
40 T data;
41 NODE_PTR leftChild;
42 NODE_PTR rightChild;
43 NODE_PTR parent; // pointer to parent node, needed by iterator
44
45 friend class BinaryTree<T>;
46 };
本文轉(zhuǎn)自:
http://www.cnblogs.com/berry/archive/2009/10/12/1581554.html
singleton模式是Gof提出的23中模式之一,也稱為單例模式,那么簡(jiǎn)單說一下,什么叫單例模式呢?
通常我們創(chuàng)建類的對(duì)象是使用new Object(),然后就調(diào)用該對(duì)象里面的方法,那么當(dāng)我們多次使用new Object()的話,會(huì)對(duì)系統(tǒng)資源造成一種浪費(fèi),當(dāng)然.net內(nèi)部已經(jīng)有垃圾回收機(jī)制可以處理這種浪費(fèi)。當(dāng)然我們并不會(huì)再程序里面多次使用new Object(),但是,作為一個(gè)類的設(shè)計(jì)者,我們需要負(fù)什么責(zé)任,除了讓別的模塊可以調(diào)用使用之外,我們的設(shè)計(jì)還需要一種規(guī)范,這也是OO里面的規(guī)范,singleton模式在這里派上了用場(chǎng)。
singleton模式的意圖:確保一個(gè)類只能擁有一個(gè)實(shí)例,并保證邏輯的正確性以及良好的效率,并提供一個(gè)該實(shí)例的全局訪問點(diǎn)。
singleton模式類型:?jiǎn)尉€程singleton,多線程singleton
singleton思路:要讓使用者只能使用一個(gè)實(shí)例的話,那么必須繞過常規(guī)的公有缺省構(gòu)造器
singleton代碼:
1 public class singleton
2 {
3 private static singleton instance;
4 private singleton() { }
5 public static singleton Instance
6 {
7 get
8 {
9 if (instance == null)
10 {
11 instance = new singleton();
12 }
13 return instance;
14 }
15 }
16 }
17
第4行:利用私有構(gòu)造函數(shù)繞開系統(tǒng)自帶的缺省公有構(gòu)造函數(shù),這樣就使類的外部不可以直接使用new實(shí)例化對(duì)象
第5行:提供一個(gè)靜態(tài)的公有屬性,供類外部調(diào)用
第9行:在這里可能存在BUG,當(dāng)有兩個(gè)線程同時(shí)操作公有屬性時(shí),常規(guī)的話應(yīng)該返回兩個(gè)一樣的實(shí)例,但是假如當(dāng)?shù)谝粋€(gè)實(shí)例還未來得及創(chuàng)建時(shí),第二個(gè)線程又訪問了它,顯然也會(huì)執(zhí)行 new singleton()這個(gè)語句,那么這兩個(gè)對(duì)象的引用就不一樣了,可以使用object.ReferenceEquals測(cè)試一下對(duì)象的引用是否一樣。因此,給大家提供多線程方案,請(qǐng)看下面代碼
1 public class singletons
2 {
3 private static volatile singletons instances = null;
4 private static object lockHelper = new object();
5 private singletons() { }
6 public static singletons Instance
7 {
8 get
9 {
10 if(instances==null)
11 {
12 lock (lockHelper)
13 {
14 if(instances==null )
15 {
16 instances = new singletons();
17 }
18 }
19 }
20 return instances;
21 }
22 }
23 }
顯然看起來與單線程singleton差不多,多了volatile 修飾符,還有一個(gè)Object對(duì)象,接下來跟大家解釋使用這些其中的緣由
volatile 修飾符
假如我定義兩個(gè)變量和兩個(gè)屬性
1 int a;
2 volatile int b;
3 public int GetFirst
4 {
5 get { return a; }
6 }
7 public int GetSecond
8 {
9 get { return b; }
10 }
GetFirst會(huì)得到當(dāng)前線程中a的值,而多個(gè)線程就會(huì)有多個(gè)a的變量拷貝,而且這些拷貝之間可以互不相同,換句話說,另一個(gè)線程可能改變了它線程內(nèi)的a值,而這個(gè)值和當(dāng)前線程中的a值不相同,那么就造成線程沖突了。
那么再來看看b,因?yàn)?span style="color: #0000ff">volatile 修飾的變量不允許有不同于“主”內(nèi)存區(qū)域的變量拷貝,換句話說,一個(gè)變量經(jīng)volatile 修飾后在所有線程中都是同步的;任何線程改變了它的值,所以其他線程立即獲取到了相同的值,當(dāng)然加了volatile 修飾的變量存儲(chǔ)時(shí)會(huì)比一般變量消耗的資源要多一點(diǎn)。
Object對(duì)象鎖
對(duì)象鎖可以保證Lock里面的代碼只能同時(shí)讓一個(gè)線程執(zhí)行,所以確保了一個(gè)對(duì)象只存在一個(gè)實(shí)例。
同樣的需求可以有不同的方法實(shí)現(xiàn),以下是另外一種實(shí)現(xiàn)singleton模式的代碼,代碼更簡(jiǎn)單,不夠有缺陷,請(qǐng)看
1 public class singletonss
2 {
3 public static readonly singletonss Instance = new singletonss();
4 private singletonss() { }
5 }
首先定義一個(gè)靜態(tài)的只讀實(shí)例,當(dāng)然也需要私有構(gòu)造器繞過缺省構(gòu)造器,這樣子也可以保證多線程里也只誕生一個(gè)對(duì)象實(shí)例,因?yàn)?Net類型初始化機(jī)制保證只有一個(gè)線程執(zhí)行了靜態(tài)構(gòu)造器。當(dāng)然這么少的代碼也可以實(shí)現(xiàn)singleton,但是靜態(tài)構(gòu)造器不支持參數(shù),也不能重構(gòu),因?yàn)樵?Net機(jī)制里面只允許一個(gè)類擁有一個(gè)靜態(tài)構(gòu)造器而且是私有的,外部不能調(diào)用只能供系統(tǒng)調(diào)用,所以我們不能使用參數(shù)。
本文轉(zhuǎn)自:http://www.cnblogs.com/magicchaiy/archive/2010/12/02/1894826.html
其他鏈接:http://www.shnenglu.com/dyj057/archive/2005/09/20/346.html
摘要: 今天開始這個(gè)系列之前,心里有些恐慌,畢竟園子里的高手關(guān)于設(shè)計(jì)模式的經(jīng)典文章很多很多,特別是大俠李會(huì)軍、呂震宇 老師的文章更是堪稱經(jīng)典。他們的文筆如行云流水,例子活潑生動(dòng),講解深入淺出。好在他們都是用C#描述,也沒有提供必要的源碼下載,所以我這里用C++實(shí) 現(xiàn)。首先我想聲明的是我的文筆絕對(duì)不如他們的好,例子也沒有他們的形象,不過我打算把C+...
閱讀全文
Active Object 模式是Command模式的一種,是實(shí)現(xiàn)多線程控制的一項(xiàng)古老技術(shù) .
在《敏捷軟件開發(fā)》這本書中描述的算法如下:
1、構(gòu)造一個(gè)命令。(實(shí)現(xiàn)Command模式的一個(gè)命令)
2、將該命令放入
Active Object Engine(也就是放入一個(gè)隊(duì)列,LinkedList)
3、從該Engine取出一個(gè)命令,執(zhí)行,若該命令沒有執(zhí)行過,設(shè)為執(zhí)行過,然后將自己加入隊(duì)列尾部,若執(zhí)行過,判斷該命令執(zhí)行需要的事件發(fā)生沒有,未發(fā)生,再將自己加入隊(duì)列尾部。事件發(fā)生了,將需要執(zhí)行的命令加入隊(duì)列尾部。
Active Object模式不屬于《Design Pattern》23模式。實(shí)際上,她是一種特殊的Command Queue。其特殊之處在于:
1. 隊(duì)列的擁有者會(huì)順序地執(zhí)行隊(duì)列中所有Command對(duì)象的Execute方法。(這個(gè)其實(shí)不算特殊)
2.Command對(duì)象在自己的Execute方法結(jié)束前,可以把一個(gè)新的command對(duì)象(實(shí)際上常常是這個(gè)command對(duì)象自己)再加到隊(duì)列的尾部。
看出來了嗎,這個(gè)隊(duì)列有可能不會(huì)終止的,他可以一直執(zhí)行下去。這個(gè)可以作為一個(gè)應(yīng)用或者服務(wù)的主模塊了,想像一下她可以作多少事情吧。
《ASP》指出這個(gè)模式可以用來在一個(gè)線程中處理多任務(wù)的問題!!! ^_^ 太cool了。
如何處理呢?你可以把每個(gè)command對(duì)象看作是一個(gè)任務(wù)。他在Execute函數(shù)中,處理自己的任務(wù),在任務(wù)告一段落時(shí),記錄自己的狀態(tài),然后把自己插入到隊(duì)列的尾部,結(jié)束Execute方法。當(dāng)隊(duì)列輪完一周后,又會(huì)再次執(zhí)行這個(gè)command對(duì)象的Execute方法。 ^_^ 很cool吧。
那么這種方法和多線程的方法相比有什么有缺點(diǎn)呢?
最大的優(yōu)點(diǎn)是,所有的command都在同一個(gè)線程中,因此切換時(shí),不需要進(jìn)入內(nèi)核模式!!超高效啊!!而且,可以有很多很多的command,數(shù)量上遠(yuǎn)遠(yuǎn)超過多線程的數(shù)量。
缺點(diǎn)嘛,是這種方法需要用戶自己來實(shí)現(xiàn)調(diào)度,另外這其實(shí)是一種非剝奪模式的多任務(wù),如果command處理不好,就會(huì)連累其它所有的command,因此實(shí)際上比多線程要更復(fù)雜。(嘿嘿,程序員能夠怕麻煩嗎?)
還有一點(diǎn),Active Object運(yùn)行于單線程,也就是說,她不能享受多處理器或多處理器核心帶來的性能上的改善。
其實(shí),這最后一點(diǎn)是非常致命的一點(diǎn)。也就是說,在當(dāng)前intel的超線程CPU機(jī)器上,如果系統(tǒng)的負(fù)擔(dān)并不重的時(shí)候。Active Object的效率有可能比多線程更低。
摘要: 引言
提起Command模式,我想沒有什么比遙控器的例子更能說明問題了,本文將通過它來一步步實(shí)現(xiàn)GOF的Command模式。
我們先看下這個(gè)遙控器程序的需求:假如我們需要為家里的電器設(shè)計(jì)一個(gè)遠(yuǎn)程遙控器,通過這個(gè)控制器,我們可以控制電器(諸如燈、風(fēng)扇、空調(diào)等)的開關(guān)。我們的控制器上有一系列的按鈕,分別對(duì)應(yīng)家中的某個(gè)電器,當(dāng)我們?cè)谶b控器上按下“On”時(shí),電器打開;當(dāng)我們按下...
閱讀全文
假設(shè)需要執(zhí)行的程序如下:
int main(int argc, char* argv[])
{
return argc;
}
執(zhí)行它,并取得其返回值,我寫了一個(gè)函數(shù)如下:
DWORD WinExecAndWait32( LPCTSTR lpszAppPath, // 執(zhí)行程序的路徑
LPCTSTR lpParameters, // 參數(shù)
LPCTSTR lpszDirectory, // 執(zhí)行環(huán)境目錄
DWORD dwMilliseconds) // 最大等待時(shí)間, 超過這個(gè)時(shí)間強(qiáng)行終止
{
SHELLEXECUTEINFO ShExecInfo = {0};
ShExecInfo.cbSize = sizeof(SHELLEXECUTEINFO);
ShExecInfo.fMask = SEE_MASK_NOCLOSEPROCESS;
ShExecInfo.hwnd = NULL;
ShExecInfo.lpVerb = NULL;
ShExecInfo.lpFile = lpszAppPath;
ShExecInfo.lpParameters = lpParameters;
ShExecInfo.lpDirectory = lpszDirectory;
ShExecInfo.nShow = SW_HIDE;
ShExecInfo.hInstApp = NULL;
ShellExecuteEx(&ShExecInfo);
// 指定時(shí)間沒結(jié)束
if (WaitForSingleObject(ShExecInfo.hProcess, dwMilliseconds) == WAIT_TIMEOUT)
{ // 強(qiáng)行殺死進(jìn)程
TerminateProcess(ShExecInfo.hProcess, 0);
return 0; //強(qiáng)行終止
}
DWORD dwExitCode;
BOOL bOK = GetExitCodeProcess(ShExecInfo.hProcess, &dwExitCode);
ASSERT(bOK);
return dwExitCode;
}
我上傳了兩個(gè)工程,希望對(duì)大家有所幫助!
下載本文轉(zhuǎn)自:
http://www.shnenglu.com/humanchao/archive/2007/12/28/39815.html
完成端口聽起來好像很神秘和復(fù)雜,其實(shí)并沒有想象的那么難。這方面的文章在論壇上能找到的我差不多都看過,寫得好點(diǎn)的就是CSDN.NET上看到的一組系列文章,不過我認(rèn)為它只是簡(jiǎn)單的翻譯了一下Network Programming for Microsoft Windows 2nd 中的相關(guān)內(nèi)容,附上的代碼好像不是原書中的,可能是另一本外文書里的。我看了以后,覺得還不如看原版的更容易理解。所以在我的開始部分,我主要帶領(lǐng)初學(xué)者理解一下完成端口的有關(guān)內(nèi)容,是我開發(fā)的經(jīng)驗(yàn),其他的請(qǐng)參考原書的相關(guān)內(nèi)容。
采用完成端口的好處是,操作系統(tǒng)的內(nèi)部重疊機(jī)制可以保證大量的網(wǎng)絡(luò)請(qǐng)求都被服務(wù)器處理,而不是像WSAAsyncSelect 和WSAEventSelect的那樣對(duì)并發(fā)的網(wǎng)絡(luò)請(qǐng)求有限制,這一點(diǎn)從上一章的測(cè)試表格中可以清楚的看出。
完成端口就像一種消息通知的機(jī)制,我們創(chuàng)建一個(gè)線程來不斷讀取完成端口狀態(tài),接收到相應(yīng)的完成通知后,就進(jìn)行相應(yīng)的處理。其實(shí)感覺就像 WSAAsyncSelect一樣,不過還是有一些的不同。比如我們想接收消息,WSAAsyncSelect會(huì)在消息到來的時(shí)候直接通知Windows 消息循環(huán),然后就可以調(diào)用WSARecv來接收消息了;而完成端口則首先調(diào)用一個(gè)WSARecv表示程序需要接收消息(這時(shí)可能還沒有任何消息到來),但是只有當(dāng)消息來的時(shí)候WSARecv才算完成,用戶就可以處理消息了,然后再調(diào)用一個(gè)WSARecv表示等待下一個(gè)消息,如此不停循環(huán),我想這就是完成端口的最大特點(diǎn)吧。
Per-handle Data 和 Per-I/O Operation Data 是兩個(gè)比較重要的概念,Per-handle Data用來把客戶端數(shù)據(jù)和對(duì)應(yīng)的完成通知關(guān)聯(lián)起來,這樣每次我們處理完成通知的時(shí)候,就能知道它是哪個(gè)客戶端的消息,并且可以根據(jù)客戶端的信息作出相應(yīng)的反應(yīng),我想也可以理解為Per-Client handle Data吧。Per-I/O Operation Data則不同,它記錄了每次I/O通知的信息,比如接收消息時(shí)我們就可以從中讀出消息的內(nèi)容,也就是和I/O操作有關(guān)的信息都記錄在里面了。當(dāng)你親手實(shí)現(xiàn)完成端口的時(shí)候就可以理解他們的不同和用途了。
CreateIoCompletionPort函數(shù)中有個(gè)參數(shù)NumberOfConcurrentThreads,完成端口編程里有個(gè)概念Worker Threads。這里比較容易引起混亂,NumberOfConcurrentThreads需要設(shè)置多少,又需要?jiǎng)?chuàng)建多少個(gè)Worker Threads才算合適?NumberOfConcurrentThreads的數(shù)目和CPU數(shù)量一樣最好,因?yàn)樯倭司蜎]法利用多CPU的優(yōu)勢(shì),而多了則會(huì)因?yàn)榫€程切換造成性能下降。Worker Threads的數(shù)量是不是也要一樣多呢,當(dāng)然不是,它的數(shù)量取決于應(yīng)用程序的需要。舉例來說,我們?cè)赪orker Threads里進(jìn)行消息處理,如果這個(gè)過程中有可能會(huì)造成線程阻塞,那如果我們只有一個(gè)Worker Thread,我們就不能很快響應(yīng)其他客戶端的請(qǐng)求了,而只有當(dāng)這個(gè)阻塞操作完成了后才能繼續(xù)處理下一個(gè)完成消息。但是如果我們還有其他的Worker Thread,我們就能繼續(xù)處理其他客戶端的請(qǐng)求,所以到底需要多少的Worker Thread,需要根據(jù)應(yīng)用程序來定,而不是可以事先估算出來的。如果工作者線程里沒有阻塞操作,對(duì)于某些情況來說,一個(gè)工作者線程就可以滿足需要了。
===========================================================
“完成端口”模型是迄今為止最為復(fù)雜的—種I/O模型。然而。假若—個(gè)應(yīng)用程序同時(shí)需要管理為數(shù)眾多的套接字,那么采用這種模型。往往可以達(dá)到最佳的系統(tǒng)性能,然而不幸的是,該模型只適用于以下操作系統(tǒng)(微軟的):Windows NT和Windows 2000操作系統(tǒng)。因其設(shè)計(jì)的復(fù)雜性,只有在你的應(yīng)用程序需要同時(shí)管理數(shù)百乃至上千個(gè)套接字的時(shí)候、而且希望隨著系統(tǒng)內(nèi)安裝的CPU數(shù)量的增多、應(yīng)用程序的性能也可以線性提升,才應(yīng)考慮采用“完成端口”模型。要記住的一個(gè)基本準(zhǔn)則是,假如要為Windows NT或windows 2000開發(fā)高性能的服務(wù)器應(yīng)用,同時(shí)希望為大量套接字I/O請(qǐng)求提供服務(wù)(Web服務(wù)器便是這方面的典型例子),那么I/O完成端口模型便是最佳選擇.
從本質(zhì)上說,完成端口模型要求我們創(chuàng)建一個(gè)Win32完成端口對(duì)象,通過指定數(shù)量的線程對(duì)重疊I/O請(qǐng)求進(jìn)行管理。以便為已經(jīng)完成的重疊I/O請(qǐng)求提供服務(wù)。要注意的是。所謂“完成端口”,實(shí)際是Win32、Windows NT以及windows 2000采用的一種I/O構(gòu)造機(jī)制,除套接字句柄之外,實(shí)際上還可接受其他東西。然而,本節(jié)只打算講述如何使用套接字句柄,來發(fā)揮完成端口模型的巨大威力。使用這種模型之前,首先要?jiǎng)?chuàng)建一個(gè)I/O完成端口對(duì)象,用它面向任意數(shù)量的套接字句柄。管理多個(gè)I/O請(qǐng)求。要做到這—點(diǎn),需要調(diào)用CreateIoCompletionPort函數(shù)。該函數(shù)定義如下:
HANDLE CreateIoCompletionPort(
HANDLE FileHandle,
HANDLE ExistingCompletionPort,
DWORD CompletionKey,
DWORD NumberOfConcurrentThreads
);
在我們深入探討其中的各個(gè)參數(shù)之前,首先要注意意該函數(shù)實(shí)際用于兩個(gè)明顯有別的目的:
■用于創(chuàng)建—個(gè)完成端口對(duì)象。
■將一個(gè)句柄同完成端口關(guān)聯(lián)到一起。
最開始創(chuàng)建—個(gè)完成端口的時(shí)候,唯一感興趣的參數(shù)便是NumberOfConcurrentThreads 并發(fā)線程的數(shù)量);前面三個(gè)參數(shù)都會(huì)被忽略。NumberOfConcurrentThreads 參數(shù)的特殊之處在于.它定義了在一個(gè)完成端口上,同時(shí)允許執(zhí)行的線程數(shù)量。理想情況下我們希望每個(gè)處理器各自負(fù)責(zé)—個(gè)線程的運(yùn)行,為完成端口提供服務(wù),避免過于頻繁的線程“場(chǎng)景”切換。若將該參數(shù)設(shè)為0,說明系統(tǒng)內(nèi)安裝了多少個(gè)處理器,便允許同時(shí)運(yùn)行多少個(gè)線程!可用下述代碼創(chuàng)建一個(gè)I/O完成端口:
CompetionPort=CreateIoCompletionPort(INVALID_HANDLE_VALUE,NULL,0,0)
該語加的作用是返問一個(gè)句柄.在為完成端口分配了—個(gè)套接字句柄后,用來對(duì)那個(gè)端
口進(jìn)行標(biāo)定(引用)。
1.工作者線程與完成端口
成功創(chuàng)建一個(gè)完成端口后,便可開始將套接字句柄與對(duì)象關(guān)聯(lián)到一起。但在關(guān)聯(lián)套接字之前、首先必須創(chuàng)建—個(gè)或多個(gè)“工作者線程”,以便在I/O請(qǐng)求投遞給完成端口對(duì)象后。為完成端口提供服務(wù)。在這個(gè)時(shí)候,大家或許會(huì)覺得奇怪、到底應(yīng)創(chuàng)建多少個(gè)線程。以便為完成端口提供服務(wù)呢?這實(shí)際正是完成端口模型顯得頗為“復(fù)雜”的—個(gè)方面, 因?yàn)榉?wù)I/O請(qǐng)求所需的數(shù)量取決于應(yīng)用程序的總體設(shè)計(jì)情況。在此要記住的—個(gè)重點(diǎn)在于,在我們調(diào)用CreateIoComletionPort時(shí)指定的并發(fā)線程數(shù)量,與打算創(chuàng)建的工作者線程數(shù)量相比,它們代表的并非同—件事情。早些時(shí)候,我們?cè)ㄗh大家用CreateIoCompletionPort函數(shù)為每個(gè)處理器都指定一個(gè)線程(處理器的數(shù)量有多少,便指定多少線程)以避免由于頻繁的線程“場(chǎng)景”交換活動(dòng),從而影響系統(tǒng)的整體性能。CreateIoCompletionPort函數(shù)的NumberofConcurrentThreads參數(shù)明確指示系統(tǒng): 在一個(gè)完成端口上,一次只允許n個(gè)工作者線程運(yùn)行。假如在完成端門上創(chuàng)建的工作者線程數(shù)量超出n個(gè).那么在同一時(shí)刻,最多只允許n個(gè)線程運(yùn)行。但實(shí)際上,在—段較短的時(shí)間內(nèi),系統(tǒng)有可能超過這個(gè)值。但很快便會(huì)把它減少至事先在CreateIoCompletionPort函數(shù)中設(shè)定的值。那么,為何實(shí)際創(chuàng)建的工作者線程數(shù)最有時(shí)要比CreateIoCompletionPort函數(shù)設(shè)定的多—些呢?這樣做有必要嗎?如先前所述。這主要取決于應(yīng)用程序的總體設(shè)計(jì)情況,假設(shè)我們的工作者線程調(diào)用了一個(gè)函數(shù),比如Sleep()或者WaitForSingleobject(),但卻進(jìn)入了暫停(鎖定或掛起)狀態(tài)、那么允許另—個(gè)線程代替它的位置。換行之,我們希望隨時(shí)都能執(zhí)行盡可能多的線程;當(dāng)然,最大的線程數(shù)量是事先在CreateIoCompletonPort調(diào)用里設(shè)定好的。這樣—來。假如事先預(yù)料到自己的線程有可能暫時(shí)處于停頓狀態(tài),那么最好能夠創(chuàng)建比CreateIoCompletionPort的NumberofConcurrentThreads參數(shù)的值多的線程.以便到時(shí)候充分發(fā)揮系統(tǒng)的潛力。—旦在完成端口上擁有足夠多的工作者線程來為I/O請(qǐng)求提供服務(wù),便可著手將套接字句柄同完成端口關(guān)聯(lián)到一起。這要求我們?cè)?#8212;個(gè)現(xiàn)有的完成端口上調(diào)用CreateIoCompletionPort函數(shù),同時(shí)為前三個(gè)參數(shù): FileHandle,ExistingCompletionPort和CompletionKey——提供套接字的信息。其中,FileHandle參數(shù)指定—個(gè)要同完成端口關(guān)聯(lián)在—一起的套接字句柄。
ExistingCompletionPort參數(shù)指定的是一個(gè)現(xiàn)有的完成端口。CompletionKey(完成鍵)參數(shù)則指定要與某個(gè)特定套接字句柄關(guān)聯(lián)在—起的“單句柄數(shù)據(jù)”,在這個(gè)參數(shù)中,應(yīng)用程序可保存與—個(gè)套接字對(duì)應(yīng)的任意類型的信息。之所以把它叫作“單句柄數(shù)據(jù)”,是由于它只對(duì)應(yīng)著與那個(gè)套接字句柄關(guān)聯(lián)在—起的數(shù)據(jù)。可將其作為指向一個(gè)數(shù)據(jù)結(jié)構(gòu)的指針、來保存套接字句柄;在那個(gè)結(jié)構(gòu)中,同時(shí)包含了套接字的句柄,以及與那個(gè)套接字有關(guān)的其他信息。就象本章稍后還會(huì)講述的那樣,為完成端口提供服務(wù)的線程例程可通過這個(gè)參數(shù)。取得與其套字句柄有關(guān)的信息。
根據(jù)我們到目前為止學(xué)到的東西。首先來構(gòu)建—個(gè)基本的應(yīng)用程序框架。
程序清單8—9向人家闡述了如何使用完成端口模型。來開發(fā)—個(gè)回應(yīng)(或“反射’)服務(wù)器應(yīng)用。
在這個(gè)程序中。我們基本上按下述步驟行事:
1) 創(chuàng)建一個(gè)完成端口。第四個(gè)參數(shù)保持為0,指定在完成端口上,每個(gè)處理器一次只允許執(zhí)行一個(gè)工作者線程。
2) 判斷系統(tǒng)內(nèi)到底安裝了多少個(gè)處理器。
3) 創(chuàng)建工作者線程,根據(jù)步驟2)得到的處理器信息,在完成端口上,為已完成的I/O請(qǐng)求提供服務(wù)。在這個(gè)簡(jiǎn)單的例子中,我們?yōu)槊總€(gè)處理器都只創(chuàng)建—個(gè)工作者線程。這是出于事先已經(jīng)預(yù)計(jì)到,到時(shí)候不會(huì)有任何線程進(jìn)入“掛起”狀態(tài),造成由于線程數(shù)量的不足,而使處理器空閑的局面(沒有足夠的線程可供執(zhí)行)。調(diào)用CreateThread函數(shù)時(shí),必須同時(shí)提供—個(gè)工作者線程,由線程在創(chuàng)建好執(zhí)行。本節(jié)稍后還會(huì)詳細(xì)討論線程的職責(zé)。
4) 準(zhǔn)備好—個(gè)監(jiān)聽套接字。在端口5150上監(jiān)聽進(jìn)入的連接請(qǐng)求。
5) 使用accept函數(shù),接受進(jìn)入的連接請(qǐng)求。
6) 創(chuàng)建—個(gè)數(shù)據(jù)結(jié)構(gòu),用于容納“單句柄數(shù)據(jù)”。 同時(shí)在結(jié)構(gòu)中存入接受的套接字句柄。
7) 調(diào)用CreateIoCompletionPort將自accept返回的新套接字句柄向完成端口關(guān)聯(lián)到 一起,通過完成鍵(CompletionKey)參數(shù),將但句柄數(shù)據(jù)結(jié)構(gòu)傳遞給CreateIoCompletionPort。
8) 開始在已接受的連接上進(jìn)行I/O操作。在此,我們希望通過重疊I/O機(jī)制,在新建的套接字上投遞一個(gè)或多個(gè)異步WSARecv或WSASend請(qǐng)求。這些I/O請(qǐng)求完成后,一個(gè)工作者線程會(huì)為I/O請(qǐng)求提供服務(wù),同時(shí)繼續(xù)處理未來的I/O請(qǐng)求,稍后便會(huì)在步驟3)指定的工作者例程中。體驗(yàn)到這一點(diǎn)。
9) 重復(fù)步驟5)—8)。直到服務(wù)器終止。
程序清單8。9 完成端口的建立
StartWinsock()
//步驟一,創(chuàng)建一個(gè)完成端口
CompletionPort=CreateIoCompletionPort(INVALI_HANDLE_VALUE,NULL,0,0);
//步驟二判斷有多少個(gè)處理器
GetSystemInfo(&SystemInfo);
//步驟三:根據(jù)處理器的數(shù)量創(chuàng)建工作線程,本例當(dāng)中,工作線程的數(shù)目和處理器數(shù)目是相同的
for(i = 0; i < SystemInfo.dwNumberOfProcessers,i++){
HANDLE ThreadHandle;
//創(chuàng)建工作者線程,并把完成端口作為參數(shù)傳給線程
ThreadHandle=CreateThread(NULL,0,
ServerWorkerThread,CompletionPort,
0, &ThreadID);
//關(guān)閉線程句柄(僅僅關(guān)閉句柄,并非關(guān)閉線程本身)
CloseHandle(ThreadHandle);
}
//步驟四:創(chuàng)建監(jiān)聽套接字
Listen=WSASocket(AF_INET,S0CK_STREAM,0,NULL,
WSA_FLAG_OVERLAPPED);
InternetAddr.sin_famlly=AF_INET;
InternetAddr.sin_addr.s_addr = htonl(INADDR_ANY);
InternetAddr.sln_port = htons(5150);
bind(Listen,(PSOCKADDR)&InternetAddr,sizeof(InternetAddr));
//準(zhǔn)備監(jiān)聽套接字
listen(Listen,5);
while(TRUE){
//步驟五,接入Socket,并和完成端口關(guān)聯(lián)
Accept = WSAAccept(Listen,NULL,NULL,NULL,0);
//步驟六 創(chuàng)建一個(gè)perhandle結(jié)構(gòu),并和端口關(guān)聯(lián)
PerHandleData=(LPPER_HANDLE_DATA)GlobalAlloc(GPTR,sizeof(PER_HANDLE_DATA));
printf("Socket number %d connected\n",Accept);
PerHandleData->Socket=Accept;
//步驟七,接入套接字和完成端口關(guān)聯(lián)
CreateIoCompletionPort((HANDLE)Accept,
CompletionPort,(DWORD)PerHandleData,0);
//步驟八
//開始進(jìn)行I/O操作,用重疊I/O發(fā)送一些WSASend()和WSARecv()
WSARecv(...)
本文轉(zhuǎn)自:http://blog.sina.com.cn/s/blog_458f4a2c0100nq44.html
基本算法貪心算法:
貪心算法 作者:
獨(dú)酌逸醉
貪心算法精講 作者:3522021224
遞歸和分治:
遞歸與分治策略 作者:
zhoudaxia圖論圖的遍歷(DFS和BFS):
圖的遍歷 作者:
jefferent最小生成樹(Prim算法和Kruskal算法):
貪心算法--最小生成樹 作者:
獨(dú)酌逸醉Dijkstra算法: 最短路徑之Dijkstra算法詳細(xì)講解 作者:綠巖
最短路徑算法—Dijkstra(迪杰斯特拉)算法分析與實(shí)現(xiàn)(C/C++) 作者:
tankywooBellman-Ford算法:最短路徑算法—Bellman-Ford(貝爾曼-福特)算法分析與實(shí)現(xiàn)(C/C++) 作者:tankywoo
Floyd-Warshall算法:最短路徑算法—Floyd(弗洛伊德)算法分析與實(shí)現(xiàn)(C/C++) 作者:tankywoo
Johnson算法:Johnson 算法 作者:huliang82
A*算法:A*算法詳解 作者:愚人有節(jié)
拓?fù)渑判颍?a title="拓?fù)渑判? >拓?fù)渑判?作者:
midgard
如何去理解 拓?fù)渑判蛩惴?/font> 作者:
張善友關(guān)鍵路徑:關(guān)鍵路徑 作者:navorse
歐拉路:歐拉路問題 作者:MaiK
差分約束:差分約束系統(tǒng) 作者:fuliang
二分圖最大匹配:二分圖匹配總結(jié) 作者:北極天南星
二分圖匹配算法總結(jié) 作者:z7m8v6
網(wǎng)絡(luò)流:網(wǎng)絡(luò)流基礎(chǔ) 作者:chhaj523
數(shù)據(jù)結(jié)構(gòu)
并查集:并查集--學(xué)習(xí)詳解 作者:yx_th000
哈希表:哈希表 作者:獵人杰二分查找:查找(二):二分查找 作者:xiaosuo
哈夫曼樹:哈夫曼樹 作者:angle平衡二叉樹: 平衡二叉樹(解惑) 作者:Never
樹狀數(shù)組:
樹狀數(shù)組總結(jié) 作者:
熊貓yingcai線段樹:
線段樹總結(jié) 作者:
星星歸并排序求逆序數(shù):
利用歸并排序求逆序數(shù) 作者:
kahn動(dòng)態(tài)規(guī)劃(DP)簡(jiǎn)單動(dòng)態(tài)規(guī)劃:
動(dòng)態(tài)規(guī)劃 作者:
brokencode背包問題:《背包九講》
數(shù)學(xué)遺傳算法:
遺傳算法入門 作者:
heaad容斥原理:
容斥原理(翻譯) 作者:
vici
母函數(shù):母函數(shù)入門小結(jié) 作者:zhangxiang0125
秦九韶算法:秦九韶算法 作者:simonezhlx
高斯消元法:歐幾里得定理(GCD):擴(kuò)展歐幾里得定理:中國(guó)剩余定理:概率問題:
計(jì)算幾何幾何公式:
離散化:
什么是離散化? 作者:
matrix67掃描線算法:
叉積和點(diǎn)積:
凸包:
本文轉(zhuǎn)自:
http://www.shnenglu.com/cxiaojia/archive/2011/11/16/rumen.html
Floyd-Warshall算法,簡(jiǎn)稱Floyd算法,用于求解任意兩點(diǎn)間的最短距離,時(shí)間復(fù)雜度為O(n^3)。
使用條件&范圍
通常可以在任何圖中使用,包括有向圖、帶負(fù)權(quán)邊的圖。
Floyd-Warshall 算法用來找出每對(duì)點(diǎn)之間的最短距離。它需要用鄰接矩陣來儲(chǔ)存邊,這個(gè)算法通過考慮最佳子路徑來得到最佳路徑。
1.注意單獨(dú)一條邊的路徑也不一定是最佳路徑。
2.從任意一條單邊路徑開始。所有兩點(diǎn)之間的距離是邊的權(quán),或者無窮大,如果兩點(diǎn)之間沒有邊相連。
對(duì)于每一對(duì)頂點(diǎn) u 和 v,看看是否存在一個(gè)頂點(diǎn) w 使得從 u 到 w 再到 v 比己知的路徑更短。如果是更新它。
3.不可思議的是,只要按排適當(dāng),就能得到結(jié)果。
偽代碼:
1 // dist(i,j) 為從節(jié)點(diǎn)i到節(jié)點(diǎn)j的最短距離
2 For i←1 to n do
3 For j←1 to n do
4 dist(i,j) = weight(i,j)
5
6 For k←1 to n do // k為“媒介節(jié)點(diǎn)”
7 For i←1 to n do
8 For j←1 to n do
9 if (dist(i,k) + dist(k,j) < dist(i,j)) then // 是否是更短的路徑?
10 dist(i,j) = dist(i,k) + dist(k,j)
我們平時(shí)所見的Floyd算法的一般形式如下:
1 void Floyd(){
2 int i,j,k;
3 for(k=1;k<=n;k++)
4 for(i=1;i<=n;i++)
5 for(j=1;j<=n;j++)
6 if(dist[i][k]+dist[k][j]<dist[i][j])
7 dist[i][j]=dist[i][k]+dist[k][j];
8 }
注意下第6行這個(gè)地方,如果dist[i][k]或者dist[k][j]不存在,程序中用一個(gè)很大的數(shù)代替。最好寫成if(dist[i] [k]!=INF && dist[k][j]!=INF && dist[i][k]+dist[k][j]
Floyd算法的實(shí)現(xiàn)以及輸出最短路徑和最短路徑長(zhǎng)度,具體過程請(qǐng)看【動(dòng)畫演示Floyd算法】。
代碼說明幾點(diǎn):
1、A[][]數(shù)組初始化為各頂點(diǎn)間的原本距離,最后存儲(chǔ)各頂點(diǎn)間的最短距離。
2、path[][]數(shù)組保存最短路徑,與當(dāng)前迭代的次數(shù)有關(guān)。初始化都為-1,表示沒有中間頂點(diǎn)。在求A[i][j]過程中,path[i][j]存放從頂點(diǎn)vi到頂點(diǎn)vj的中間頂點(diǎn)編號(hào)不大于k的最短路徑上前一個(gè)結(jié)點(diǎn)的編號(hào)。在算法結(jié)束時(shí),由二維數(shù)組path的值回溯,可以得到從頂點(diǎn)vi到頂點(diǎn)vj的最短路徑。
初始化A[][]數(shù)組為如下,即有向圖的鄰接矩陣。
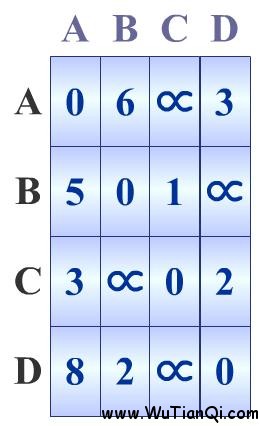
完整的實(shí)現(xiàn)代碼如下:
1 #include <iostream>
2 #include <string>
3 #include <stdio.h>
4 using namespace std;
5 #define MaxVertexNum 100
6 #define INF 32767
7 typedef struct
8 {
9 char vertex[MaxVertexNum];
10 int edges[MaxVertexNum][MaxVertexNum];
11 int n,e;
12 }MGraph;
13
14 void CreateMGraph(MGraph &G)
15 {
16 int i,j,k,p;
17 cout<<"請(qǐng)輸入頂點(diǎn)數(shù)和邊數(shù):";
18 cin>>G.n>>G.e;
19 cout<<"請(qǐng)輸入頂點(diǎn)元素:";
20 for (i=0;i<G.n;i++)
21 {
22 cin>>G.vertex[i];
23 }
24 for (i=0;i<G.n;i++)
25 {
26 for (j=0;j<G.n;j++)
27 {
28 G.edges[i][j]=INF;
29 if (i==j)
30 {
31 G.edges[i][j]=0;
32 }
33 }
34 }
35 for (k=0;k<G.e;k++)
36 {
37 cout<<"請(qǐng)輸入第"<<k+1<<"條弧頭弧尾序號(hào)和相應(yīng)的權(quán)值:";
38 cin>>i>>j>>p;
39 G.edges[i][j]=p;
40 }
41 }
42 void Dispath(int A[][MaxVertexNum],int path[][MaxVertexNum],int n);
43
44 void Floyd(MGraph G)
45 {
46 int A[MaxVertexNum][MaxVertexNum],path[MaxVertexNum][MaxVertexNum];
47 int i,j,k;
48 for (i=0;i<G.n;i++)
49 {
50 for (j=0;j<G.n;j++)
51 {
52 A[i][j]=G.edges[i][j];
53 path[i][j]=-1;
54 }
55 }
56 for (k=0;k<G.n;k++)
57 {
58 for (i=0;i<G.n;i++)
59 {
60 for (j=0;j<G.n;j++)
61 {
62 if (A[i][j]>A[i][k]+A[k][j])
63 {
64 A[i][j]=A[i][k]+A[k][j];
65 path[i][j]=k;
66 }
67 }
68 }
69 }
70 Dispath(A,path,G.n);
71 }
72
73 void Ppath(int path[][MaxVertexNum],int i,int j)
74 {
75 int k;
76 k=path[i][j];
77 if (k==-1)
78 {
79 return;
80 }
81 Ppath(path,i,k);
82 printf("%d,",k);
83 Ppath(path,k,j);
84 }
85
86 void Dispath(int A[][MaxVertexNum],int path[][MaxVertexNum],int n)
87 {
88 int i,j;
89 for (i=0;i<n;i++)
90 {
91 for (j=0;j<n;j++)
92 {
93 if (A[i][j]==INF)
94 {
95 if (i!=j)
96 {
97 printf("從%d到%d沒有路徑\n",i,j);
98 }
99 }
100 else
101 {
102 printf(" 從%d到%d=>路徑長(zhǎng)度:%d路徑:",i,j,A[i][j]);
103 printf("%d,",i);
104 Ppath(path,i,j);
105 printf("%d\n",j);
106 }
107 }
108 }
109 }
110
111 int main()
112 {
113 freopen("input2.txt", "r", stdin);
114 MGraph G;
115 CreateMGraph(G);
116 Floyd(G);
117 return 0;
118 }
測(cè)試結(jié)果如下:
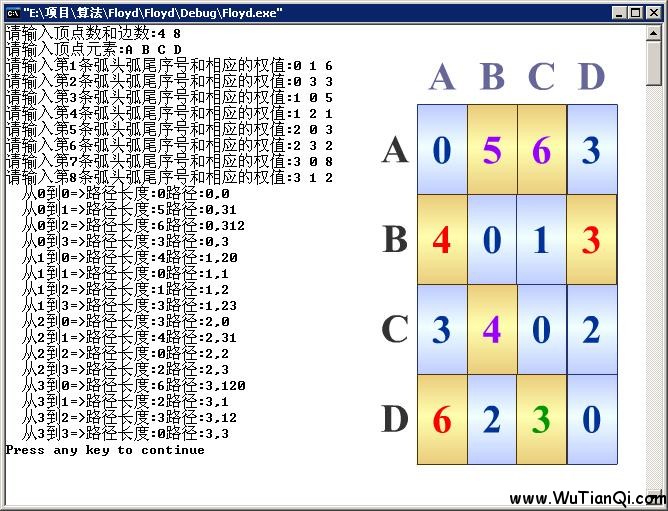
本文轉(zhuǎn)自:http://www.wutianqi.com/?p=1903