Floyd-Warshall算法,簡稱Floyd算法,用于求解任意兩點間的最短距離,時間復(fù)雜度為O(n^3)。
使用條件&范圍
通常可以在任何圖中使用,包括有向圖、帶負權(quán)邊的圖。
Floyd-Warshall 算法用來找出每對點之間的最短距離。它需要用鄰接矩陣來儲存邊,這個算法通過考慮最佳子路徑來得到最佳路徑。
1.注意單獨一條邊的路徑也不一定是最佳路徑。
2.從任意一條單邊路徑開始。所有兩點之間的距離是邊的權(quán),或者無窮大,如果兩點之間沒有邊相連。
對于每一對頂點 u 和 v,看看是否存在一個頂點 w 使得從 u 到 w 再到 v 比己知的路徑更短。如果是更新它。
3.不可思議的是,只要按排適當,就能得到結(jié)果。
偽代碼:
1 // dist(i,j) 為從節(jié)點i到節(jié)點j的最短距離
2 For i←1 to n do
3 For j←1 to n do
4 dist(i,j) = weight(i,j)
5
6 For k←1 to n do // k為“媒介節(jié)點”
7 For i←1 to n do
8 For j←1 to n do
9 if (dist(i,k) + dist(k,j) < dist(i,j)) then // 是否是更短的路徑?
10 dist(i,j) = dist(i,k) + dist(k,j)
我們平時所見的Floyd算法的一般形式如下:
1 void Floyd(){
2 int i,j,k;
3 for(k=1;k<=n;k++)
4 for(i=1;i<=n;i++)
5 for(j=1;j<=n;j++)
6 if(dist[i][k]+dist[k][j]<dist[i][j])
7 dist[i][j]=dist[i][k]+dist[k][j];
8 }
注意下第6行這個地方,如果dist[i][k]或者dist[k][j]不存在,程序中用一個很大的數(shù)代替。最好寫成if(dist[i] [k]!=INF && dist[k][j]!=INF && dist[i][k]+dist[k][j]
Floyd算法的實現(xiàn)以及輸出最短路徑和最短路徑長度,具體過程請看【動畫演示Floyd算法】。
代碼說明幾點:
1、A[][]數(shù)組初始化為各頂點間的原本距離,最后存儲各頂點間的最短距離。
2、path[][]數(shù)組保存最短路徑,與當前迭代的次數(shù)有關(guān)。初始化都為-1,表示沒有中間頂點。在求A[i][j]過程中,path[i][j]存放從頂點vi到頂點vj的中間頂點編號不大于k的最短路徑上前一個結(jié)點的編號。在算法結(jié)束時,由二維數(shù)組path的值回溯,可以得到從頂點vi到頂點vj的最短路徑。
初始化A[][]數(shù)組為如下,即有向圖的鄰接矩陣。
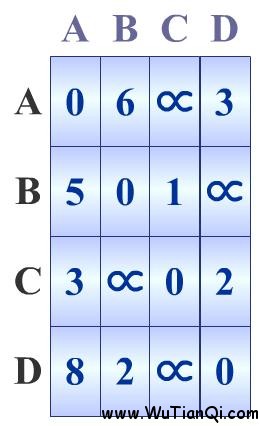
完整的實現(xiàn)代碼如下:
1 #include <iostream>
2 #include <string>
3 #include <stdio.h>
4 using namespace std;
5 #define MaxVertexNum 100
6 #define INF 32767
7 typedef struct
8 {
9 char vertex[MaxVertexNum];
10 int edges[MaxVertexNum][MaxVertexNum];
11 int n,e;
12 }MGraph;
13
14 void CreateMGraph(MGraph &G)
15 {
16 int i,j,k,p;
17 cout<<"請輸入頂點數(shù)和邊數(shù):";
18 cin>>G.n>>G.e;
19 cout<<"請輸入頂點元素:";
20 for (i=0;i<G.n;i++)
21 {
22 cin>>G.vertex[i];
23 }
24 for (i=0;i<G.n;i++)
25 {
26 for (j=0;j<G.n;j++)
27 {
28 G.edges[i][j]=INF;
29 if (i==j)
30 {
31 G.edges[i][j]=0;
32 }
33 }
34 }
35 for (k=0;k<G.e;k++)
36 {
37 cout<<"請輸入第"<<k+1<<"條弧頭弧尾序號和相應(yīng)的權(quán)值:";
38 cin>>i>>j>>p;
39 G.edges[i][j]=p;
40 }
41 }
42 void Dispath(int A[][MaxVertexNum],int path[][MaxVertexNum],int n);
43
44 void Floyd(MGraph G)
45 {
46 int A[MaxVertexNum][MaxVertexNum],path[MaxVertexNum][MaxVertexNum];
47 int i,j,k;
48 for (i=0;i<G.n;i++)
49 {
50 for (j=0;j<G.n;j++)
51 {
52 A[i][j]=G.edges[i][j];
53 path[i][j]=-1;
54 }
55 }
56 for (k=0;k<G.n;k++)
57 {
58 for (i=0;i<G.n;i++)
59 {
60 for (j=0;j<G.n;j++)
61 {
62 if (A[i][j]>A[i][k]+A[k][j])
63 {
64 A[i][j]=A[i][k]+A[k][j];
65 path[i][j]=k;
66 }
67 }
68 }
69 }
70 Dispath(A,path,G.n);
71 }
72
73 void Ppath(int path[][MaxVertexNum],int i,int j)
74 {
75 int k;
76 k=path[i][j];
77 if (k==-1)
78 {
79 return;
80 }
81 Ppath(path,i,k);
82 printf("%d,",k);
83 Ppath(path,k,j);
84 }
85
86 void Dispath(int A[][MaxVertexNum],int path[][MaxVertexNum],int n)
87 {
88 int i,j;
89 for (i=0;i<n;i++)
90 {
91 for (j=0;j<n;j++)
92 {
93 if (A[i][j]==INF)
94 {
95 if (i!=j)
96 {
97 printf("從%d到%d沒有路徑\n",i,j);
98 }
99 }
100 else
101 {
102 printf(" 從%d到%d=>路徑長度:%d路徑:",i,j,A[i][j]);
103 printf("%d,",i);
104 Ppath(path,i,j);
105 printf("%d\n",j);
106 }
107 }
108 }
109 }
110
111 int main()
112 {
113 freopen("input2.txt", "r", stdin);
114 MGraph G;
115 CreateMGraph(G);
116 Floyd(G);
117 return 0;
118 }
測試結(jié)果如下:
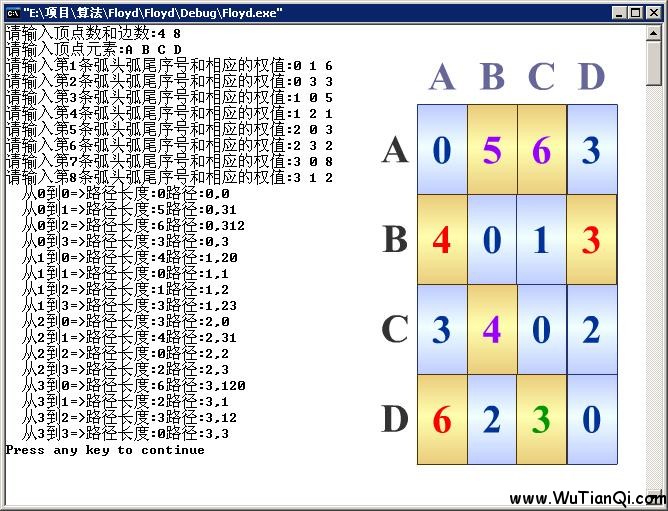
本文轉(zhuǎn)自:http://www.wutianqi.com/?p=1903
posted on 2012-06-30 16:18
王海光 閱讀(11410)
評論(2) 編輯 收藏 引用 所屬分類:
算法