計數排序:
今天學習了計數排序,貌似計數排序的復雜度為o(n)。很強大。他的基本思路為:
1.
我們希望能線性的時間復雜度排序,如果一個一個比較,顯然是不實際的,書上也在決策樹模型中論證了,比較排序的情況為nlogn的復雜度。
2.
既然不能一個一個比較,我們想到一個辦法,就是如果我在排序的時候就知道他的位置,那不就是掃描一遍,把他放入他應該的位置不就可以了嘛。
3.
要知道他的位置,我們只需要知道有多少不大于他不就可以了嗎?
4.
以此為出發點,我們怎么確定不大于他的個數呢?我們先來個約定,如果數組中的元素都比較集中,都在[0, max]范圍內。我們開一個max的空間b數組,把b數組下標對應的元素和要排序的A數組下標對應起來。這樣不就可以知道不比他大的有多少個了嗎?我們只要把比他小的位置元素個數求和,就是不比他大的。例如:A={3,5,7};我們開一個大小為8的數組b,把a[0] = 3 放入b[3]中,使b[3] = 0; 同理 b[5] = 1; b[7] = 2;其他我們都設置為-1,哈哈我們只需要遍歷一下b數組,如果他有數據,就來出來,鐵定是當前最小的。如果要知道比a[2]小的數字有多少個,值只需要求出b[0] – b[6]的有數據的和就可以了。這個0(n)的速度不是蓋得。
5.
思路就是這樣咯。但是要注意兩個數相同的情況A = {1,2,3,3,4},這種情況就不可以咯,所以還是有點小技巧的。
6.
處理小技巧:我們不把A的元素大小與B的下標一一對應,而是在B數組對應處記錄該元素大小的個數。這不久解決了嗎。哈哈。例如A =
{1,2,3,3,4}我們開大小為5的數組b;記錄數組A中元素值為0的個數為b[0] = 0, 記錄數組A中元素個數為1的b[1] = 1,同理b[2] = 1, b[3] = 2, b[4] = 1;好了,這樣我們就知道比A[4](4)小的元素個數是多少了:count = b[0] + b[1] +
b[2] + b[3] = 4;他就把A[4]的元素放在第4個位置。
還是截張書上的圖:
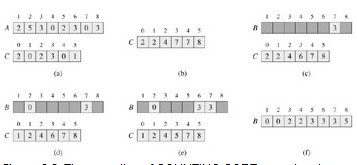
再次推薦《算法導論》這本書,在我的上次的隨筆中有下載鏈接。哈哈。真正支持還是需要買一下紙版。呵呵。
7. 不過在編程的時候還是要注意細節的,例如我不能每次都來算一下比他小的個數。呵呵,思路就這樣了。奉上源代碼:
#include <stdio.h>
#include <stdlib.h>
//計數排序
int CountSort(int* pData, int nLen)
{
int* pCout = NULL; //保存記數數據的指針
pCout = (int*)malloc(sizeof(int) * nLen); //申請空間
//初始化記數為0
for (int i = 0; i < nLen; ++i)
{
pCout[i] = 0;
}
//記錄排序記數。在排序的值相應記數加1。
for (int i = 0; i < nLen; ++i)
{
++pCout[pData[i]]; //增
}
//確定不比該位置大的數據個數。
for (int i = 1; i < nLen; ++i)
{
pCout[i] += pCout[i - 1]; //不比他大的數據個數為他的個數加上前一個的記數。
}
int* pSort = NULL; //保存排序結果的指針
pSort = (int*)malloc(sizeof(int) * nLen); //申請空間
for (int i = 0; i < nLen; ++i)
{
//把數據放在指定位置。因為pCout[pData[i]]的值就是不比他大數據的個數。
//為什么要先減一,因為pCout[pData[i]]保存的是不比他大數據的個數中包括了
//他自己,我的下標是從零開始的!所以要先減一。
--pCout[pData[i]]; //因為有相同數據的可能,所以要把該位置數據個數減一。
pSort[pCout[pData[i]]] = pData[i];
}
//排序結束,復制到原來數組中。
for (int i = 0; i < nLen; ++i)
{
pData[i] = pSort[i];
}
//最后要注意釋放申請的空間。
free(pCout);
free(pSort);
return 1;
}
int main()
{
int nData[10] = {8,6,3,6,5,8,3,5,1,0};
CountSort(nData, 10);
for (int i = 0; i < 10; ++i)
{
printf("%d ", nData[i]);
}
printf("\n");
system("pause");
return 0;
}