
2025年4月25日
本文主要闡述用兩種方法判斷給定兩個(gè)二元二次型是否相似,相似情況下的具體變換。
相似變換如果確定了,也利于判斷正定性,因?yàn)橄嗨贫涡偷恼ㄐ韵嗤?br />
基本定義
下述定義來自文獻(xiàn)[1] 12.1節(jié),有所擴(kuò)展

變換求解 先來看運(yùn)用解方程的方法

再來看用矩陣的觀點(diǎn)方法,求解變換。這種方法更適合求解到對角型的變換


參考文獻(xiàn)
[1] 華羅庚文集數(shù)論卷2
[2] 高等代數(shù) 丘維聲
posted @
2025-04-25 19:05 春秋十二月 閱讀(72) |
評論 (0) |
編輯 收藏

2025年4月22日
【命題1】 所有群同態(tài)的原像個(gè)數(shù)相同,即為核的大小

下面看下這個(gè)結(jié)論在文獻(xiàn)[1]中3.2節(jié)的應(yīng)用

【命題2】所有元素階小于等于2 的群為交換群,且其階為2的整數(shù)冪

該結(jié)論在
https://zhuanlan.zhihu.com/p/644888274中的推論2.2證明中用到
【命題3】群中任一元的相對于正規(guī)子群的指數(shù)次冪屬于正規(guī)子群,2階正規(guī)子群必
屬于群的中心

【定理】模奇合數(shù)的既約乘法群,其中雅可比符號(hào)為1的元素構(gòu)成它的子群,其階為
既約乘法群群階的一半

參考文獻(xiàn)
[1] 橢圓曲線及其在密碼學(xué)中的應(yīng)用—導(dǎo)引 Andreas Enge
[2] 抽象代數(shù)I 趙春來 徐明曜
[3] 華羅庚文集數(shù)論卷2
[4] 組合數(shù)學(xué) 馮榮權(quán) 宋春偉
posted @
2025-04-22 21:18 春秋十二月 閱讀(112) |
評論 (0) |
編輯 收藏

2024年11月10日
符號(hào)含義
E 表示滿足橢圓曲線Weierstrass方程上的點(diǎn)群
K 代數(shù)閉域,用來限制Weierstrass方程的系數(shù)與E中的點(diǎn)
E(K) 定義在K上的點(diǎn)群E
E/K 定義在K上的橢圓曲線E
End(E) E上的自同態(tài)環(huán)
域擴(kuò)張分析

End(E)模與Z代數(shù)

極點(diǎn)首項(xiàng)系數(shù)


除子映射及同構(gòu)

同種映射同態(tài)性的解釋



Hasse定理之引理證明的補(bǔ)充

撓曲線及其個(gè)數(shù)

有限域上的橢圓曲線
一種確定型群階計(jì)算法

奇素域上的算法應(yīng)用


GF域上的群階計(jì)算


Schoof算法正確性根本
一種計(jì)算橢圓曲線群的階的確定型多項(xiàng)式時(shí)間算法,確定型是因?yàn)樗惴▋?nèi)部沒有隨機(jī)選擇/概率拋幣操作,多項(xiàng)式時(shí)間是因?yàn)橛?em>k的乘法與求逆總次數(shù)是O((logq)^6)
(
q為
k的大小,乘法與求逆相對加減運(yùn)算顯著耗時(shí))。具體原理及流程詳見參考文獻(xiàn)[1]中5.2節(jié)。這里給出筆者的一些思考
1. Hasse定理(Frobenius自同態(tài)方程式)在扭點(diǎn)群上的限制亦成立,這決定了t模l的一個(gè)同余方程成立,且在模l的最小非負(fù)剩余系下解是唯一的
2. 孫子定理保證了某取值范圍內(nèi)的一個(gè)t模L(L為各素因子l的乘積)的唯一解,即由t模L各個(gè)素因子l的同余方程構(gòu)成的同余方程組的解是唯一的
3. L必須大于t取值上限的2倍。這是為了算法求得的解滿足上述2(否則在更小的L內(nèi)得到的解不唯一,因L與t上限或下限間的某數(shù)可以與t模L同余)
4. 素因子l的選擇排除2與橢圓曲線特征p。這是因?yàn)樗惴?gòu)造所依賴的一個(gè)引理之前提條件:為奇素?cái)?shù)保證l次除子多項(xiàng)式屬于k[X],即引理論斷有意義;
不等于p保證檢測一個(gè)多項(xiàng)式f是否零多項(xiàng)式的充要條件成立,即可以用l次除子多項(xiàng)式去整除f來判斷。另l為素?cái)?shù)保證了與其它除子多項(xiàng)式(及其冪次)互素
另外發(fā)現(xiàn)了算法的一處瑕疵,即第4步預(yù)計(jì)算除子多項(xiàng)式與Frobenius自同態(tài)的復(fù)合少了兩個(gè)值,這導(dǎo)致第5步可能崩潰,當(dāng)依賴的后續(xù)兩個(gè)復(fù)合多項(xiàng)式?jīng)]被計(jì)算時(shí)。
這個(gè)糾正可通過修改第4步擴(kuò)大2個(gè)值,或第5步通過除子多項(xiàng)式的遞推公式按需計(jì)算
扭點(diǎn)的階計(jì)算正確性根本

在密碼學(xué)中的應(yīng)用
選取原則
1. 排除超奇異橢圓曲線。這是為避免MOV等約化攻擊,約化攻擊時(shí)間復(fù)雜度是亞指數(shù)
2. 有限域的選擇要使E(Fq)的群階足夠大。這是為了緩解Shanks及Pollard ρ攻擊
3. E(Fq)存在階為大素?cái)?shù)的子群。這是為了抵抗Pohlig-Hellman攻擊
對于第1點(diǎn),就排除了char(K)=2或3且j(E)=0對應(yīng)的如下標(biāo)準(zhǔn)形式曲線
Y2+α3Y=X3+α4X+α6(α3≠0) 與 Y2=X3+α4X+α6
一種典型方案
橢圓曲線及有限域的選擇使得|E(Fq)|=cm,且char(Fq) ∤ q+1-cm。其中m是一個(gè)大素?cái)?shù)(通常不低于256位二進(jìn)制長度,提供中長期安全性),c小于m。
m階子群的生成元可通過以下方法確定:隨機(jī)選擇E上的一個(gè)有理點(diǎn)P,如果Q=cP為零元(即無窮遠(yuǎn)點(diǎn)),則重復(fù)選擇,直到其不等于零元。
一旦找到了生成元,那么子群就可以構(gòu)造出來了。下面分析正確性

參考文獻(xiàn)
[1] 橢圓曲線及其在密碼學(xué)中的應(yīng)用—導(dǎo)引 Andreas Enge
[2] 算法數(shù)論 裴定一、祝躍飛
[3] The Arithmetic of Elliptic Curves Joseph H. Silverman
[4] 標(biāo)識(shí)密碼學(xué) 程朝輝
[5] 代數(shù)學(xué)基礎(chǔ)與有限域 林東岱
[6] 抽象代數(shù)I 趙春來 徐明曜
[7] 代數(shù)與數(shù)論 李超 周悅
posted @
2024-11-10 21:45 春秋十二月 閱讀(286) |
評論 (0) |
編輯 收藏

2024年9月7日
原本算法
摘抄參考文獻(xiàn)1中附錄的算法流程如下

例子測驗(yàn)


改正后的算法
改正之前,先理清原本算法判別不可約多項(xiàng)式所用的原理。其原理是若f(x)可約,當(dāng)且僅當(dāng)存在次數(shù)i<=d=[deg(f(x))/2]的不可約因子g(x),而此時(shí)gcd(x
q^i-x, f(x))≠1。
根據(jù)
參考文獻(xiàn)2(詳見如下定理),x
q^i-x是所有i次不可約多項(xiàng)式的乘積,因此它必定包含g(x)而與f(x)存在公因子。不可約判別算法的思想應(yīng)該是遍歷次數(shù)1到d的所有不可約多項(xiàng)式
(沒必要檢測大于d的不可約多項(xiàng)式,因?yàn)槿鬴(x)可約則其分解因子中必定存在不大于d的不可約多項(xiàng)式),檢測輸入多項(xiàng)式與它們是否存在公因子。所以這個(gè)原理是正確的,只是實(shí)現(xiàn)不對,
略作改正如下(類c語言描述)

重新測驗(yàn)


參考文獻(xiàn)
[1] 算法數(shù)論 裴定一、祝躍飛
[2] 代數(shù)學(xué)基礎(chǔ)與有限域 林東岱
posted @
2024-09-07 23:07 春秋十二月 閱讀(309) |
評論 (0) |
編輯 收藏

2024年8月30日
通用算法
先摘抄參考文獻(xiàn)[1]中的算法流程如下

正確性分析
下面證明以上算法用到的事實(shí)結(jié)論,提煉為如下幾個(gè)引理

 算法構(gòu)造思想
算法構(gòu)造思想
用到二次剩余知識(shí),即一個(gè)待求平方元ɑ可以且只能表示為兩個(gè)平方因子的乘積,其中一因子為任意隨機(jī)選取的非平方因子β的偶數(shù)冪,
另一因子為葉子群H的一元素r,H作為陪集劃分根群(有限域乘法群)得到β生成的集合即商群G/H的一個(gè)代表元系。這樣一來,將開方轉(zhuǎn)化為β與r的乘方運(yùn)算,
迭代的過程就是為求那個(gè)具體的代表元β
e中的指數(shù)e(注意e必為偶數(shù)),從G
s-2到G
0=H,迭代結(jié)束后r被唯一確定,r的開方等于r的(t+1)/2次方(因?yàn)閠是H的階且為奇數(shù),r
t+1=r)。
觀察算法流程,可以發(fā)現(xiàn)如果分解q-1后得到s=1,那么就沒必要選取非平方元β了(這時(shí)令β=1),直接跳到第6步得到結(jié)果。僅當(dāng)s≠1才隨機(jī)選取β。這樣改進(jìn)后可加快算法運(yùn)行
例子測驗(yàn)


特殊算法
當(dāng)q是素?cái)?shù)且q≡3(mod 4)時(shí),存在更快的算法及測驗(yàn)如下

參考文獻(xiàn)
[1] 算法數(shù)論 裴定一、祝躍飛
posted @
2024-08-30 22:22 春秋十二月 閱讀(431) |
評論 (0) |
編輯 收藏

2024年8月15日
基本原理

再來看Terr算法用到的如下定理
定理 (基于
參考文獻(xiàn)1改正后的描述)
對每一正整數(shù)t,存在唯一確定的一組整數(shù)k和j,0<=k<j,使得t=Tj+1-k,其中T0=0,Tn=Tn-1+n-1,n>=1

如果t=0,那么j在區(qū)間[0,1),故只能取0,此時(shí)k=0與條件k<j矛盾,若允許k=j,則不保證唯一,比如t=1 => j=1, k=0 或 j=2, k=2。
所以參考文獻(xiàn)1中原來定理的描述“對每一非負(fù)整數(shù)t”是錯(cuò)誤的。下面列舉一些實(shí)例驗(yàn)證j與k的唯一解
t=1 => j=1, k=0
t=2 => j=2, k=1
t=3 => j=2, k=0
t=4 => j=3, k=2
t=5 => j=3, k=1
t=6 => j=3, k=0
算法偽代碼

例子測驗(yàn)

參考文獻(xiàn)
[1] 代數(shù)學(xué)基礎(chǔ)與有限域 林東岱
posted @
2024-08-15 22:35 春秋十二月 閱讀(703) |
評論 (0) |
編輯 收藏

2024年6月29日
私鑰分組加密


上圖的證明中,r
(j)兩兩不同的概率計(jì)算是關(guān)鍵,下面給出詳細(xì)過程

另外兩個(gè)分布統(tǒng)計(jì)的不同意味著計(jì)算可分辨(反之則計(jì)算不可分辨),亦即r(j)至少兩個(gè)相同的概率。
Construction 5.3.9一次只能加密與密鑰等長的明文,如果要加密更長的明文,怎么辦?一個(gè)簡單直接
的方法是將明文分成多個(gè)大小為n的塊,對每個(gè)塊調(diào)用上述加密步驟,那么就得到形如下的密文塊序列
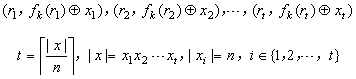
密文塊序列從
Proposition 5.3.10的證明中可知是計(jì)算不可分辨的,滿足
「多組消息安全性
」。但對于解密
需要存儲(chǔ)每一塊的隨機(jī)數(shù),因此比較占空間,所以衍生出下面更高效的方案
Construction 5.3.12
私密通用加密

語義安全性分析


抗主動(dòng)攻擊安全性
以上兩種構(gòu)造因滿足
「多組消息安全性
」,故滿足
CPA與
CCA1,具體的證明可參考Oded Goldreich《密碼學(xué)基礎(chǔ)》的
Proposition 5.4.12、
Proposition 5.4.18。
但不滿足
CCA2,因?yàn)楣粽吣玫教魬?zhàn)密文后,可以修改它再發(fā)出解密質(zhì)疑,得到回答的明文從而異或求解
fk(
ri),最后與挑戰(zhàn)密文異或求解挑戰(zhàn)明文
對于通用加密構(gòu)造的CCA2攻擊細(xì)節(jié)如下
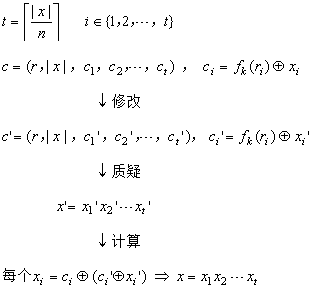
posted @
2024-06-29 17:00 春秋十二月 閱讀(633) |
評論 (0) |
編輯 收藏

2024年5月16日
定義

Berlekamp分解算法

AES有限域

不可約性證明
 非本原性驗(yàn)證
非本原性驗(yàn)證

找出本原元

不可約多項(xiàng)式個(gè)數(shù)

線性移位寄存器m序列
根據(jù)參考文獻(xiàn)1知線生移位寄存器產(chǎn)生m序列的充要條件是特征多項(xiàng)式f(x)為本原多項(xiàng)式。而確立有限域上的本原多項(xiàng)式,主要有兩種方法:
一種方法是根據(jù)
Fq上所有次數(shù)為n的本原多項(xiàng)式的乘積正好等于割圓多項(xiàng)式Q
e,其中e=q
n-1,從而所有次數(shù)為n的本原多項(xiàng)式可以通過分解Q
e得到。
另一種方法是通過構(gòu)造本原元再求本原元的極小多項(xiàng)式,先素因子分解q
n-1=p
1p
2...p
k,如果對每一p
i都有ord(
αi)=p
i,那么
α=
α1α2...
αk的階就是q
n-1,
因此是
Fq上的本原元,則f(x)=(x-
α)(x-
α2)...(x-
αr),r=q
n-1(因?yàn)?span style="color: #4b4b4b; font-family: Verdana, Geneva, Arial, Helvetica, sans-serif; font-size: 13px; background-color: #ffffff;">α是本原元,所以n是使
αq^n=
α成立的最小正整數(shù))。
求解本原多項(xiàng)式
假設(shè)線性移位寄存器的級(jí)數(shù)為4,這里使用上述二種方法求
F16上的本原多項(xiàng)式,過程如下
分解割圓多項(xiàng)式法 
構(gòu)造極小多項(xiàng)式法 


本原多項(xiàng)式個(gè)數(shù)

m序列示例

參考文獻(xiàn)
[1] 代數(shù)學(xué)基礎(chǔ)與有限域 林東岱
posted @
2024-05-16 13:41 春秋十二月 閱讀(907) |
評論 (0) |
編輯 收藏

2024年4月4日
【適用前提】大整數(shù)N=pq的素因子p<q<2p,解密指數(shù)d<(1/3)N
1/4
【攻擊方法】 1)用歐幾里得算法計(jì)算e/N的各個(gè)漸近分?jǐn)?shù)k
i/d
i,i>=1,直至d
i>=(1/3)N
1/4,記錄此時(shí)的i為m。令i=1
2)計(jì)算T=(e*d
i-1)/k
i,若T不為整數(shù)則轉(zhuǎn)到4),否則轉(zhuǎn)到3)
3)解方程f(x)=x
2-(N-T+1)x+N=0的根,如果有正整數(shù)根且兩個(gè)根皆小于N,則輸出p、q,并返回成功。否則轉(zhuǎn)到4)
4)遞增i,若i<m則轉(zhuǎn)回2),否則返回失敗
該方法即
Wiener算法用到了關(guān)于連分?jǐn)?shù)的一個(gè)
定理:若α為任一實(shí)數(shù),有理數(shù)p/q適合|α-(p/q)|<1/(2q2),則p/q必為α的某一漸近分?jǐn)?shù)。證明詳見參考文獻(xiàn)[2]。
由定理可知攻擊方法是可行的,必能找到使f(x)=0有合理解的某漸近分?jǐn)?shù)。下面證明:攻擊迭代次數(shù)的上界為
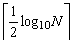 【證明】
【證明】

【例子】N = 9449868410449,e = 6792605526025,d<(1/3)N
1/4≈584,試分解N
 參考文獻(xiàn)
參考文獻(xiàn)
[1] 公鑰密碼學(xué)的數(shù)學(xué)基礎(chǔ) 王小云、王明強(qiáng)、孟憲萌
[2] 算法數(shù)論 裴定一、祝躍飛
posted @
2024-04-04 18:19 春秋十二月 閱讀(635) |
評論 (0) |
編輯 收藏
本博客所有隨筆均為原創(chuàng),因?yàn)椴欢ㄆ诰S護(hù)更新,所以轉(zhuǎn)載請注明出處,如有問題和建議,請留言或評論,發(fā)表您的寶貴意見,藉此平臺(tái)以分享交流、共同進(jìn)步。
聯(lián)系方式:微信theory-math
|
|
| 29 | 30 | 31 | 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 1 | 2 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
常用鏈接
留言簿(74)
隨筆分類(158)
隨筆檔案(159)
文章分類(30)
關(guān)注的開源項(xiàng)目
最新隨筆
積分與排名
最新評論

閱讀排行榜
評論排行榜