私鑰分組加密


上圖的證明中,r
(j)兩兩不同的概率計算是關鍵,下面給出詳細過程

另外兩個分布統(tǒng)計的不同意味著計算可分辨(反之則計算不可分辨),亦即r(j)至少兩個相同的概率。
Construction 5.3.9一次只能加密與密鑰等長的明文,如果要加密更長的明文,怎么辦?一個簡單直接
的方法是將明文分成多個大小為n的塊,對每個塊調用上述加密步驟,那么就得到形如下的密文塊序列
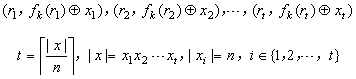
密文塊序列從
Proposition 5.3.10的證明中可知是計算不可分辨的,滿足
「多組消息安全性
」。但對于解密
需要存儲每一塊的隨機數(shù),因此比較占空間,所以衍生出下面更高效的方案
Construction 5.3.12
私密通用加密

語義安全性分析


抗主動攻擊安全性
以上兩種構造因滿足
「多組消息安全性
」,故滿足
CPA與
CCA1,具體的證明可參考Oded Goldreich《密碼學基礎》的
Proposition 5.4.12、
Proposition 5.4.18。
但不滿足
CCA2,因為攻擊者拿到挑戰(zhàn)密文后,可以修改它再發(fā)出解密質疑,得到回答的明文從而異或求解
fk(
ri),最后與挑戰(zhàn)密文異或求解挑戰(zhàn)明文
對于通用加密構造的CCA2攻擊細節(jié)如下
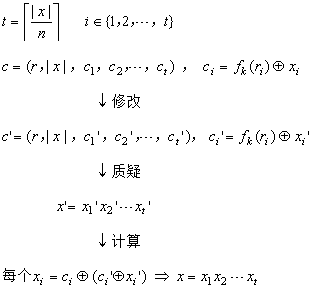
posted on 2024-06-29 17:00
春秋十二月 閱讀(664)
評論(0) 編輯 收藏 引用 所屬分類:
Algorithm