Posted on 2011-12-11 11:52
eryar 閱讀(2382)
評論(0) 編輯 收藏 引用

在前面的章節中,我提到過節點矢量有兩種類型:open和periodic。還分為均勻的和非均勻的。我將對此進和詳細講解,并推出它們所表示的基函數。我只給出k次基函數,當然你也可以根據需要推導出低次基函數。本節中的每張圖片都是由本章程序所產生的。在本章的結尾,我將會對顯示任意次數的基函數進行解釋。
Open節點矢量推導出的基函數跟上節中的基函數很像,所以就以此開始吧。
準均勻節點矢量 Open Knot Vectors
準均勻節點矢量的節點序列中兩端節點具有重復度k,剩余的其它節點序列可以是均勻也可以是非均勻的。舉例如下:
k = 3 [X] = [0 0 0 1 2 3 3 3] (uniform)
k = 4 [X] = [0 0 0 0 1 1 1 1] (uniform)
k = 3 [X] = [0 0 0 1 1 2 2 2] (nonuniform)
k = 2 [X] = [0 0 1 2 3 3 3 4 5 6 6] (nonuniform)
節點矢量端部的重復值是為確保曲線上的首未兩點與第一個和最后一個控制頂點對應。他們的作用就是把曲線的端部拉到控制多邊形的端部。這是由于重復的節點矢量值可以把曲線的首未點值限制。也可確保端部的斜率等于控制多邊形首未側的斜率。這樣以來,端部條件和Bezier曲線一樣,就便于曲線的拼接。
在上一節點,我說過Bezier曲線就是B樣條曲線的節點矢量為準均勻時的特例。你若要通過四個控制頂點,并且節點矢量的端部條件由準均勻節點矢量確定來定義一個三次B樣條曲線,其實這就是Bezier曲線。B樣條曲線的優勢在于你可用多個控制頂點并且保證端部條件,還可以設置曲線的次數。如有10個控制頂點的Bezier曲線將會推導出一個9次曲線。相應的B樣條曲線的節點矢量為:[X] = [0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1]。有10個控制頂點和B樣條曲線若用如下的節點矢量可能會推導出一個三次曲線。[X] = [0 0 0 0 1 2 3 4 5 6 6 6 6]
有幾個優點:你可以控制曲線的次數;也有更多的局部修改功能。圖4.8所示為k=10的Bezier曲線和k=4的B樣條曲線。觀察一下局部修改的能力:

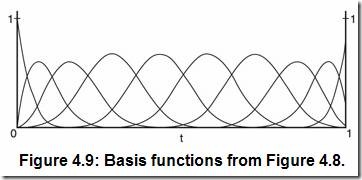
選擇使用準均勻節點矢量的主要原因是可以把曲線的端點限制在控制多邊形的端點上。這在曲線拼接時特別有用,但是這也是把雙刃劍。圖4.9所示為繪制圖4.8的B樣條曲線的基函數的圖形。如圖所示,每個基函數有點不同。
周期性節點矢量 Periodic Knot Vectors
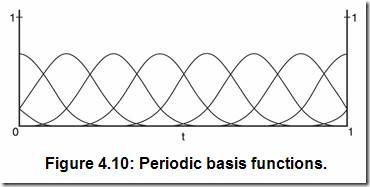
在第二章的“三角函數”中,我引入了周期函數,像正弦函數和余弦函數。這些函數是周期性因為每個周期的波形都可以認為是相同的波形在重復。若可以由節點矢量推導出周期性的基函數,則節點矢量也是周期性的。如下為均勻周期節點矢量(k=4, N=10)可推出周期性的基函數如圖4.10所示。
[X] = [1 2 3 4 5 6 7 8 9 10 11 12 13 14]
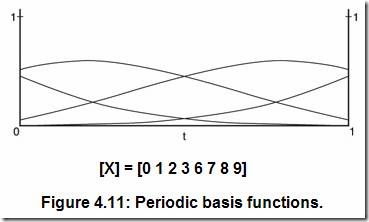
周期性的節點矢量也不一定是均勻的。如圖4.11所示為由非均勻節點矢量(k=4, N=10)推導出的周期性基函數。盡管在圖4.11中可能很難看出,每個基函數都是一樣的,只是偏移了,只能看到它的部分。