Posted on 2010-08-07 21:37
MiYu 閱讀(1187)
評論(0) 編輯 收藏 引用 所屬分類:
ACM ( 數論 ) 、
ACM ( 組合 )

MiYu原創, 轉帖請注明 : 轉載自 ______________白白の屋
題目地址:
http://acm.hdu.edu.cn/showproblem.php?pid=2067
題目描述:
Problem Description
小兔的叔叔從外面旅游回來給她帶來了一個禮物,小兔高興地跑回自己的房間,拆開一看是一個棋盤,小兔有所失望。不過沒過幾天發現了棋盤的好玩之處。從起點(0,0)走到終點(n,n)的最短路徑數是C(2n,n),現在小兔又想如果不穿越對角線(但可接觸對角線上的格點),這樣的路徑數有多少?小兔想了很長時間都沒想出來,現在想請你幫助小兔解決這個問題,對于你來說應該不難吧!
Input
每次輸入一個數n(1<=n<=35),當n等于-1時結束輸入。
Output
對于每個輸入數據輸出路徑數,具體格式看Sample。
Sample Input
1
3
12
-1
Sample Output
1 1 2
2 3 10
3 12 416024
題目分析:
假設小兔的棋盤是 8 × 8 的 ( 當然你也可以假設是其他 )。如下圖:
箭頭方向表示從該格子下一步能去的格子。因為不能穿越對角線,所有對角線上的格子只有進去的箭頭,沒有出來的箭頭。
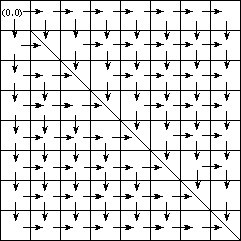
觀察上圖你就可以發現,其實這是一張關于對角線對稱的圖。所有我們只要求一個方向的值,然后乘以2即可。
我們就拿下三角來考慮。不難發現,所有在0列上的格子,路徑數都是
1 (只能從上面過來)。
而其他格子則都是由上、左兩個方向過來,即:
f(i, j) = f(i - 1, j) + f(i, j - 1);
另外
f(i, i) = f(i, j - 1) 或者 f(i, i) = f( i-1, j ) ;
代碼如下:
MiYu原創, 轉帖請注明 : 轉載自 ______________白白の屋
#include<iostream>
using namespace std;
typedef long long int64;
int64 f[37][37];
int main()
{
int ca=0;
int N;
while ( cin >> N , N + 1 )
{
++ ca;
for ( int i = 1;i <= N; ++ i )
{
f[0][i] = 1;
}
for ( int i = 1; i < N; ++ i )
{
for ( int j = i; j <= N; ++ j )
{
if ( i == j )
{
f[i][j] = f[i-1][j];
}
else
{
f[i][j] = f[i-1][j] + f[i][j-1];
}
}
}
printf("%d %d %I64d\n", ca, N, 2 * f[N-1][N] );
}
return 0;
}
另外看別人的解題報告說這個是卡特蘭數 ( 詳細請查看
<<卡特蘭數>> ), 其實現在還不理解, 分析如下:
Catalan數。。
令h(1)=1,h(0)=1,catalan數滿足遞歸式:
h(n)= h(0)*h(n-1)+h(1)*h(n-2) +  + h(n-1)h(0) (其中n>=2)
+ h(n-1)h(0) (其中n>=2)
另類遞歸式:
h(n)=((4*n-2)/(n+1))*h(n-1);
該遞推關系的解為:
h(n)=C(2n,n)/(n+1) (n=1,2,3,…)
附卡特蘭代碼:
#include<stdio.h>
int main()
{
__int64 a[37][37]={0};
int i,j,n,t=0;
a[0][0]=0;
a[0][1]=1;
a[1][1]=2;
for(i=2;i<37;i++)
{
a[i][0]=1;
for(j=1;j<i-1;j++)
a[i][j]=a[i][j-1]+a[i-1][j];
a[i][i-1]=a[i][i-2]+a[i-1][i-1]/2;
a[i][i]=2*a[i][i-2]+a[i-1][i-1];
}
while(scanf("%d",&n)&&n!=-1)
{
printf("%d %d %I64d\n",++t,n,a[n][n]);
}
return 0;
}