以下是我从网上收集的关于l合博弈的资料汇总：(x)
有一U很有意思的游戏Q就是有物体若干堆，可以是火柴棍或是围棋子等{均可。两?br>从堆中取物体若qԌ规定最后取光物体者取胜。这是我国民间很古老的一个游?br>Q别看这游戏极其单，却蕴含着深刻的数学原理。下面我们来分析一下要如何才能?br>取胜?/p>
Q一Q?strong>巴什博奕QBash GameQ：(x)只有一堆n个物品，两个从q堆物品中取物，?br>定每ơ至取一个，最多取m个。最后取光者得胜?/span>
昄Q如果n=m+1Q那么由于一ơ最多只能取m个，所以，无论先取者拿走多个Q?br>后取者都能够一ơ拿走剩余的物品Q后者取胜。因此我们发C如何取胜的法则：(x)如果 可以看出,a0=b0=0,ak是未在前面出现过的最自然数,?bk= ak + kQ奇异局势有 1。Q何自然数都包含在一个且仅有一个奇异局势中?br> ׃ak是未在前面出现过的最自然数Q所以有ak > ak-1 Q?bk= ak + k > ak 假设面对的局势是Qa,bQ，?b = aQ则同时从两堆中取走 a 个物体，变Z 从如上性质可知Q两个h如果都采用正操作，那么面对非奇异局势，先拿者必?br>Q反之，则后拿者取胜?/p> 那么ȝ一个局势（aQbQ，怎样判断它是不是奇异局势呢Q我们有如下公式Q?/p> ak =[kQ?+√5Q?2]Qbk= ak + k Qk=0Q?Q?Q?#8230;,n Ҏ(gu)可C取整函? Q三Q?span style="font-family: 'Courier New'; color: rgb(255, 0, 0); ">姆博奕QNimm GameQ：(x)
n=Qm+1Qr+sQ（rZQ意自然数Qs≤m),那么先取者要拿走s个物品，如果后取者拿?br>kQ?#8804;m)个，那么先取者再拿走m+1-k个，l果剩下Qm+1Q（r-1Q个Q以后保持这L(fng)
取法Q那么先取者肯定获胜。MQ要保持l对手留下（m+1Q的倍数Q就能最后获胜?br> q个游戏q可以有一U变相的玩法Q两个h轮流报数Q每ơ至报一个，最多报?br>个，谁能报到100者胜?br>Q二Q?strong>威佐夫博奕（Wythoff GameQ：(x)有两堆各若干个物品，两个从某一堆或?br>时从两堆中取同样多的物品Q规定每ơ至取一个，多者不限，最后取光者得胜?br>
q种情况下是颇ؓ(f)复杂的。我们用QakQbkQ（ak ≤ bk ,k=0Q?Q?Q?#8230;,n)表示
两堆物品的数量ƈU其?strong>局?/strong>Q如果甲面对Q?Q?Q，那么甲已l输了，q种局势我?br>UCؓ(f)奇异局?/strong>。前几个奇异局势是Q（0Q?Q、（1Q?Q、（3Q?Q、（4Q?Q、（6Q?br>10Q、（8Q?3Q、（9Q?5Q、（11Q?8Q、（12Q?0Q?/p>
如下三条性质Q?/p>
-1 + k-1 = bk-1 > ak-1 。所以性质1。成立?br> 2。Q意操作都可将奇异局势变为非奇异局ѝ?br> 事实上，若只改变奇异局势（akQbkQ的某一个分量，那么另一个分量不可能在其
他奇异局势中Q所以必然是非奇异局ѝ如果QakQbkQ的两个分量同时减少Q则?br>于其差不变，且不可能是其他奇异局势的差，因此也是非奇异局ѝ?br> 3。采用适当的方法，可以非奇异局势变为奇异局ѝ?/p>
奇异局势（0Q?Q；如果a = ak Qb > bkQ那么，取走b – bk个物体，卛_为奇异局
势；如果 a = ak Q?nbsp; b < bk ,则同时从两堆中拿?ak – ab – ak个物?变ؓ(f)奇异局
势（ ab – ak , ab – ak+ b – akQ；如果a > ak Qb= ak + k,则从W一堆中拿走多余
的数量a – ak 卛_Q如果a < ak Qb= ak + k,分两U情况，W一U，a=aj Qj < kQ?br>,从第二堆里面拿走 b – bj 卛_Q第二种Qa=bj Qj < kQ?从第二堆里面拿走 b – a
j 卛_?/p>
奇妙的是其中出现了黄金分割数Q?+√5Q?2 = 1?18…,因此,由akQbkl成的矩形近
gؓ(f)黄金矩ŞQ由?/Q?+√5Q?Q?#8730;5-1Q?2Q可以先求出j=[aQ?#8730;5-1Q?2]Q若a=[
jQ?+√5Q?2]Q那么a = ajQbj = aj + jQ若不等于，那么a = aj+1Qbj+1 = aj+1
+ j + 1Q若都不是，那么׃是奇异局ѝ然后再按照上述法则q行Q一定会(x)遇到奇异
局ѝ?/p>
物品Q规定每ơ至取一个，多者不限，最后取光者得胜?/span>
q种情况最有意思，它与二进制有密切关系Q我们用QaQbQcQ表C某U局势，?br>先（0Q?Q?Q显然是奇异局势，无论谁面对奇异局势，都必然失败。第二种奇异局势是
Q?QnQnQ，只要与对手拿C样多的物品，最后都导_(d)0Q?Q?Q。仔l分析一
下，Q?Q?Q?Q也是奇异局势，无论Ҏ(gu)如何拿，接下来都可以变ؓ(f)Q?QnQnQ的?br>形?/p>
计算机算法里面有一U叫做按位模2加，也叫做异或的q算Q我们用W号Q?Q表C?br>q种q算。这U运和一般加法不同的一Ҏ(gu)1+1=0。先看（1Q?Q?Q的按位?加的l?br>果：(x)
1 =二进?1
2 =二进?0
3 =二进?1 Q?Q?br>——————?br>0 =二进?0 Q注意不q位Q?/p>
对于奇异局势（0QnQnQ也一Pl果也是0?/p>
M奇异局势（aQbQcQ都有aQ?QbQ?Qc =0?/p>
如果我们面对的是一个非奇异局势（aQbQcQ，要如何变为奇异局势呢Q假?a < b
< c,我们只要?c 变ؓ(f) aQ?Qb,卛_,因ؓ(f)有如下的q算l果: aQ?QbQ?Q?aQ?Q?br>b)=(aQ?Qa)Q?Q?bQ?Qb)=0Q?Q?=0。要c 变ؓ(f)aQ?QbQ?span style="font-family: 'Courier New'; color: rgb(0, 128, 0); ">只要?c中减?c-Q?br>aQ?QbQ即可?br>
?。（14Q?1Q?9Q，14Q?Q?1=27Q?9-27=12Q所以从39中拿?2个物体即可达
到奇异局势（14Q?1Q?7Q?/p>
?。（55Q?1Q?21Q，55Q?Q?1=102Q?21-102=19Q所以从121中拿?9个物?br>Ş成了奇异局势（55Q?1Q?02Q?/p>
?。（29Q?5Q?8Q，29Q?Q?5=48Q?8-48=10Q从58中拿?0个，变ؓ(f)Q?9Q?
5Q?8Q?/p>
?。我们来实际q行一盘比赛看看：(x)
?(7,8,9)->(1,8,9)奇异局?br> ?(1,8,9)->(1,8,4)
?(1,8,4)->(1,5,4)奇异局?br> ?(1,5,4)->(1,4,4)
?(1,4,4)->(0,4,4)奇异局?br> ?(0,4,4)->(0,4,2)
?(0.4,2)->(0,2,2)奇异局?br> ?(0,2,2)->(0,2,1)
?(0,2,1)->(0,1,1)奇异局?br> ?(0,1,1)->(0,1,0)
?(0,1,0)->(0,0,0)奇异局?br> 甲胜?/p>
题目1Q今有若q堆火柴Q两Zơ从中拿取，规定每次只能从一堆中取若q根Q?nbsp;
可将一堆全取走Q但不可不取Q最后取完者ؓ(f)胜，求必胜的Ҏ(gu)?nbsp;
题目2Q今有若q堆火柴Q两Zơ从中拿取，规定每次只能从一堆中取若q根Q?nbsp;
可将一堆全取走Q但不可不取Q最后取完者ؓ(f)负，求必胜的Ҏ(gu)?br>嘿嘿Q这个游戏我早就见识q了。小时候用珠算玩这个游戏：(x)W一档拨一个，W二档拨两个Q依ơ直到第五档拨五个。然后两个hp再把棋子拨下来Q谁要是最后一个拨谁就赢。有一ơ暑假看见两个小孩子在玩q个游戏Q我在x没有一个定论呢。下面就来试着证明一下吧
先解决第一个问题吧?br>定义Q若所有火柴数异或?Q则该状态被UCؓ(f)利他态，用字母T表示Q否则，
为利己态，用S表示?br>[定理1]Q对于Q何一个S态，总能从一堆火柴中取出若干个之成为T态?br>证明Q?br> 若有n堆火_(d)每堆火柴有A(i)根火柴数Q那么既然现在处于S态，
c = A(1) xor A(2) xor … xor A(n) > 0;
把c表示成二q制Q记它的二进制数的最高位为第p位，则必然存在一个A(t),它二q制的第p位也?。（否则Q若所有的A(i)的第p位都?Q这与c的第p位就也ؓ(f)0矛盾Q?br> 那么我们把x = A(t) xor c,则得到x < A(t).q是因ؓ(f)既然A(t)的第p位与c的第p位同?,那么x的第p位变?,而高于p的位q没有改变。所以x < A(t).?br> A(1) xor A(2) xor … xor x xor … xor A(n)
= A(1) xor A(2) xor … xor A(t) xor c xor … xor A(n)
= A(1) xor A(2) xor… xor A(n) xor A(1) xor A(2) xor … xor A(n)
= 0
q就是说从A(t)堆中取出 A(t) – x 根火柴后状态就?x)从S态变为T态。证?br>[定理2]QT态，取Q何一堆的若干根，都将成ؓ(f)S态?br>证明Q用反证法试试?br> ?br> c = A(1) xor A(2) xor … xor A(i) xor … xor A(n) = 0Q?br> c’ = A(1) xor A(2) xor … xor A(i’) xor c xor … xor A(n) = 0;
则有
c xor c’ = A(1) xor A(2) xor … xor A(i) xor … xor A(n) xor A(1) xor A(2) xor … xor A(i’) xor c xor … xor A(n) = A(i) xor A(i’) =0
q而推出A(i) = A(i’)Q这与已知矛盾。所以命题得证?br>[定理 3]QS态，只要Ҏ(gu)正确Q必赢?nbsp;
最l胜利即由S态{变ؓ(f)T态，M一个S态，只要把它变ؓ(f)T态，Q由定理1Q可以把它变成T态。）Ҏ(gu)只能把T态{变ؓ(f)S?定理2)。这P所有S态向T态的转变都可以有己方控制Q对方只能被动地实现由T态{变ؓ(f)S态。故S态必赢?br>[定理4]QT态，只要Ҏ(gu)法正，必|?nbsp;
由定?易得?nbsp;
接着来解决第二个问题?br>定义Q若一堆中仅有1根火_(d)则被UCؓ(f)孤单堆。若大于1根，则称为充裕堆?br>定义QT态中Q若充裕堆的堆数大于{于2Q则UCؓ(f)完全利他态，用T2表示Q若充裕堆的堆数{于0Q则UCؓ(f)部分利他态，用T0表示?br>
孤单堆的Ҏ(gu)异或只会(x)影响二进制的最后一位，但充裕堆?x)媄响高位（非最后一位）。一个充裕堆Q高位必有一位不?Q则所有根数异或不?。故不会(x)是T态?br>[定理5]QS0态，即仅有奇C孤单堆，必|。T0态必胜?nbsp;
证明Q?br>S0态，其实是每次只能取一栏V每ơ第奇数栚w由己取，W偶数根都由?nbsp;
方取Q所以最后一根必己取。|。同? T0态必?
[定理6]QS1态，只要Ҏ(gu)正确Q必胜?nbsp;
证明Q?br>若此时孤单堆堆数为奇敎ͼ把充裕堆取完Q否则，取成一栏V这P变成奇C孤单堆，由对方取。由定理5Q对方必输。己必胜?nbsp; #
[定理7]QS2态不可{一ơ变为T0态?nbsp;
证明Q?br>充裕堆数不可能一ơ由2变ؓ(f)0。得证?nbsp; #
[定理8]QS2态可一ơ{变ؓ(f)T2态?nbsp;
证明Q?br>由定?QS态可转变为T态，态可一ơ{变ؓ(f)T态，又由定理6QS2态不可{一ơ变为T0态，所以{变的T态ؓ(f)T2态?nbsp; #
[定理9]QT2态，只能转变为S2态或S1态?nbsp;
证明Q?br>由定?QT态必然变为S态。由于充裕堆C可能一ơ由2变ؓ(f)0Q所以此时的S态不可能为S0态。命题得证?nbsp;
[定理10]QS2态，只要Ҏ(gu)正确Q必?
证明Q?br>Ҏ(gu)如下Q?nbsp;
1Q?nbsp; S2态，把它变为T2态。（由定?Q?nbsp;
2Q?nbsp; Ҏ(gu)只能T2转变成S2态或S1态（定理9Q?br> 若{变ؓ(f)S2, 转向1Q?nbsp;
若{变ؓ(f)S1, q己必胜。（定理5Q?nbsp;
[定理11]QT2态必输?nbsp;
证明Q同10?nbsp;
lg所qͼ必输态有Q?nbsp; T2,S0
必胜态：(x) S2,S1,T0.
两题比较Q?nbsp;
W一题的全过E其实如下：(x)
S2->T2->S2->T2-> …… ->T2->S1->T0->S0->T0->……->S0->T0(?)
W二题的全过E其实如下：(x)
S2->T2->S2->T2-> …… ->T2->S1->S0->T0->S0->……->S0->T0(?)
下划U表C利一方的取法?nbsp; 是否发现了他们的惊h怼之处?nbsp;
我们不难发现(见加黑部?QS1态可以{变ؓ(f)S0态（W二题做法）Q也可以转变?nbsp;
T0Q第一题做法）。哪一Ҏ(gu)制了S1态，他即可以有办法自己得到最后一根（转变?nbsp;
T0Q?也可以Ҏ(gu)得到最后一根（转变为S0Q?nbsp;
所以，抢夺S1是制胜的关键Q?nbsp;
为此Q始l把T2态让l对方，Ҏ(gu)处于被动状态，他早晚将把状态变为S1.
http://acm.hdu.edu.cn/showproblem.php?pid=1907
http://acm.hdu.edu.cn/showproblem.php?pid=2509
看完上面的结论，p利解决上面2道了
子最q迷途于博弈之中。。。感触颇深?br>Z让大家能够在学习(fn)博弈的时候少走弯路，最重要的也是ؓ(f)了加pq影响Q温故而知斎ͼ特发此脓(chung)与大家共勉?br>学博弈先从概念开始：(x)
特别推荐LCY老师的课Ӟ(x)博弈入门?br>下蝲地址Q?a id="url_5" target="_blank" style="color: rgb(41, 112, 166); text-decoration: none; ">http://acm.hdu.edu.cn/forum/read.php?tid=6875
q个课g个h认ؓ(f)从博弈的基本思想Q一直到解博弈的中心法做了很好的诠释。但是特别要注意的是。课件后面一部分p写的讲义是重中之重。小子英语很弱，在这困扰很久。现在ؓ(f)大家大概介绍一下?br>主要是后l点和SG值的问题:
SG|(x)一个点的SG值就是一个不{于它的后点的SG的且大于{于零的最整数?br>后点：(x)也就是按照题目要求的走法Q比如取矛_可以取的数量Q方法）能够C步达到的那个炏V?br>具体的有关SG值是怎么q用的希望大家自己多x?br>课g后面有一?536的代码。可以放在后面做?br>看到q里推荐大家做几道题Q?846Q最单的博弈水题Q?br>1847Q求SG|
有了上面的知识接下来我们来看看组合博弈（n堆石子）
推荐大家看个资料Q?br>博弈-取石子游?推荐{五星U?
http://acm.hdu.edu.cn/forum/read.php?fid=20&tid=5748
http://hi.baidu.com/netnode/blog/item/30932c2edc7384514fc226ea.html
q里提出了一个奇异状态的问题。看了这文章你?x)发现异或运在博弈中用的妙处。当然这里指出的只是l合博弈中一U特D情c?br>王道q是对SG值的求解Q但是知道这么一U思\无疑Ҏ(gu)维的广度和深度扩展是很有帮助的?br>ZZ博弈
http://acm.hdu.edu.cn/forum/read.php?fid=9&tid=10617
q里介绍了组和博弈的两种大的cdQ一U是最后取的是N状态一U是最后取的是P状态，两个状态的解题Ҏ(gu)能看懂很有帮助。当Ӟ能够把推DE理解，吃透无疑是大牛U的做法~子也佩服的紧~
1536题推荐做做这题，q题前面提醒大家是一个求SG值的题目Q题目前面是对异或运运用在l合博弈问题中的很好的解释。当焉目本w是有所不同的。因为在q里面对取法有所要求。那么这样就回归C解决博弈问题的王道算法——求SGg?br> 有关q用求SG值的博弈题目有：(x) 1850Q也可基于奇异状态异或）
1848Q中和的大斐波那契数列的典型求SG值题Q?br>1517Q个为有点猥琐的题目。。。。在此题上困扰很久。当然搞出来很开心。小子是用比较规矩的求SG值的Ҏ(gu)求出来的Q但是论坛有人对其推出来了规律，q里佩服一下，大家可以学习(fn)一下）
1079Q更猥琐的题目，Ҏ(gu)手要求较高，因ؓ(f)按传l方法需要比较细致的模拟加对边角状态的考虑Q同h人推出来了公式）
当你全部看完以上的东ѝ做完以上的题目的话。。。小子恭喜你~你博弈入门了~~~~
q里子告诉大家。博弈很强大。学?fn)要耐心~谢谢
Current System Time : 2008-12-11 19:16:03
ACM课作业：(x)
1001 Brave Game
1002 Good Luck in CET-4 Everybody!
1003 Fibonacci again and again
1004 Rabbit and Grass
1005 Being a Good Boy in Spring Festival
1006 Public Sale
1007 (zhn)念512汶川大地震遇隑?yu)——选拔志愿?nbsp;
1008 kiki’s game
1009 Calendar Game
1010 A Multiplication Game
1011 Digital Deletions
1012 S-Nim
http://acm.hdu.edu.cn/forum/read.php?tid=11339&fpage=0&toread=&page=1
Copy code
//博弈-Z求SG?br>//Accepted 1536 578MS 416K 904 B
#include”iostream”
using namespace std;
int f[101],sg[10001],k;
int mex(int b)
{
int a[101]={0},i;
for(i=0;i<k;i++)
{
if(b-f<0)//b-f后?br> break;
if(sg[b-f]==-1)
{
sg[b-f]=mex(b-f);
}
a[sg[b-f]]=1;
}
for(i=0;i<k;i++)
if(!a)
{
return i;
}
}
int main()
{
int i,t,n,s,bead,j;
while(cin >> k,k)
{
for(i=0;i<k;i++)
{
cin >> f;
}
memset(sg,-1,sizeof(sg));
for(i=0;i<k;i++)
for(j=i+1;j<k;j++)
if(f>f[j])
{
f+=f[j];
f[j]=f-f[j];
f-=f[j];
}
sg[0]=0;
cin >> t;
while(t–)
{
cin >> n;
s=0;
while(n–)
{
cin >> bead;//该堆的成员个?br> if(sg[bead]==-1)
sg[bead]=mex(bead);
s=s^sg[bead];
}
if(s==0)
cout << “L”;
else
cout << “W”;
}
cout << endl;
}
return 0;
}
Copy code
//博弈-Z求SG?br>//Accepted 1517 234MS 0K 837 B
#include”iostream”
using namespace std;
int main()
{
__int64 a[7000]={1},min,n;
int p[10],sg[7000],i,j,k;
for(i=2;i<10;p=0,i++);
for(i=1;i<7000;i++)
{
for(j=2,min=-1;j<10;j++)
if(min==-1||a[p[j]]*j<a[p[min]]*min)
min=j;
a=a[p[min]]*min;
min=a[p[min]]*min;
if(a>=5000000000)
break;
for(j=2;j<10;j++)
if(a[p[j]]*j==min)
p[j]++;
}//从小到大求出所有乘U?br> while(scanf(“%I64d”,&n)!=EOF)
{
for(i=0;i<7000;i++)
{
sg=0;
if(a>=n)
break;
}
for(j=i-1;a[j]*9>=n&&j>=0;j–)
sg[j]=1;
while(j>=0)
{
for(k=j+1;k<i&&a[j]*9>=a[k];k++)
if(a[k]%a[j]==0&&sg[k]==0)
{
sg[j]=1;
break;
}
j–;
}
puts(sg[0]?”Stan wins.”:”Ollie wins.”);
}
return 0;
}
q里感谢shǎ崽同学的一D代码让子学会(x)了puts的妙?/em>
#include”iostream”
using namespace std;
int main()
{
int temp,t,n,s,x,i;
cin >> t;
while(t–)
{
cin >> n;
for(i=s=temp=0;i<n;i++)
{
cin >> x;
if(x>1) temp=1;
s^=x;
}
if((s&&temp)||(!s&&!temp))
cout << “John” << endl;
else
cout << “Brother” << endl;
}
return 0;
}
]]>
题目地址:
http://acm.hdu.edu.cn/showproblem.php?pid=2147
题目描述:
Time Limit: 5000/1000 MS (Java/Others) Memory Limit: 40000/1000 K (Java/Others)
Total Submission(s): 1806 Accepted Submission(s): 1055
Problem Description
Recently kiki has nothing to do. While she is bored, an idea appears in his mind, she just playes the checkerboard game.The size of the chesserboard is n*m.First of all, a coin is placed in the top right corner(1,m). Each time one people can move the coin into the left, the underneath or the left-underneath blank space.The person who can't make a move will lose the game. kiki plays it with ZZ.The game always starts with kiki. If both play perfectly, who will win the game?
Input
Input contains multiple test cases. Each line contains two integer n, m (0<n,m<=2000). The input is terminated when n=0 and m=0.
Output
If kiki wins the game printf "Wonderful!", else "What a pity!".
Sample Input
5 3
5 4
6 6
0 0
Sample Output
What a pity!
Wonderful!
Wonderful!
题目分析:
分析如下:
P点：(x)是P个石子的时候，Ҏ(gu)拿可以赢(自己输的)
N点：(x)是N个石子的时候，自己拿可以赢
现在关于P,N的求解有三个规则
Q?Q：(x)最l态都是P
Q?Q：(x)按照游戏规则Q到辑ֽ前态的前态都是N的话Q当前态是P
Q?Q：(x)按照游戏规则Q到辑ֽ前态的前态至有一个P的话Q当前态是N
题意Q?/p>
在一个m*n的棋盘内Q从(1,m)点出发，每次可以q行的移动是Q左UMQ下UMQ左下移一。然后kiki每次先走Q判断kiki时候会(x)赢（Ҏ(gu)无\可走的时候）?/p>
我们可以把PN状态的Ҏ(gu)l出来：(x)Q?/p>
q些点的描绘有一个程序：(x)Q?/p>
?/p>
#include<iostream>
using namespace std;
bool map[2001][2001];//1 P 0 N;
int main(){
int i,j,k;
map[1][1]=1;
for(i=2;i<=2000;i++)
{
if(map[i-1][1])
map[i][1]=0;
else map[i][1]=1;
for(j=2;j<i;j++){
if(!map[i][j-1]&&!map[i-1][j-1]&&!map[i-1][j])
map[i][j]=1;
else map[i][j]=0;
}
if(map[1][i-1])
map[1][i]=0;
else map[1][i]=1;
for(j=2;j<i;j++){
if(!map[j-1][i]&&!map[j-1][i-1]&&!map[j][i-1])
map[j][i]=1;
else map[j][i]=0;
}
if(!map[i][i-1]&&!map[i-1][i-1]&&!map[i-1][i])
map[i][i]=1;
else map[i][i]=0;
}
int M,N;
for(i=1;i<=10;i++){
for(j=1;j<=10;j++)
printf("%c ",map[i][j]?'P':'N');
printf("\n");
}
while(scanf("%d%d",&M,&N)&&M&&N){
if(map[M][N]) printf("What a pity!\n");
else printf("Wonderful!\n");
}
return 0;
}
?/p>
具体代码如下:
using namespace std;
int main ()
{
int n,m;
while ( cin >> n >> m , n + m )
{
puts ( n%2 && m % 2 ? "What a pity!" : "Wonderful!");
}
return 0;
}
]]>
题目地址:
http://acm.hdu.edu.cn/showproblem.php?pid=2149
题目描述:
Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 719 Accepted Submission(s): 419
Problem Description
虽然不想Q但是现实d是现实，Lele始终没有逃过退学的命运Q因Z没有拿到奖学金。现在等待他的，是像FarmJohn一L(fng)农田生?br>
要种田得有田才行QLele听说街上正在举行一场别开生面的拍卖会(x)Q拍卖的物品正好是一?0亩的田地。于是，Lele带上他的全部U蓄Q冲往拍卖?x)?br>
后来发现Q整个拍卖会(x)只有Lele和他的死对头Yueyue?br>
通过打听QLele知道q场拍卖的规则是q样的：(x)刚开始底价ؓ(f)0Q两个h轮流开始加P不过每次加h(hun)的幅度要?～N之间Q当h大于或等于田地的成本?nbsp;M Ӟd方就把这块田地卖l这ơ叫L(fng)人?br>
Lele和Yueyue虽然考试不行Q但是对拍卖却十分精通，而且他们两个人都十分惛_到这块田地。所以他们每ơ都是选对自己最有利的方式进行加仗?br>
׃Lele字典序比Yueyue靠前Q所以每ơ都是由Lele先开始加P请问Q第一ơ加L(fng)时候，
Lele要出多少才能保证自己买得到这块地呢？
Input
本题目包含多l测试，请处理到文gl束(EOF)。每l测试占一行?br>每组试包含两个整数M和N(含义见题目描qͼ0<NQM<1100)
Output
对于每组数据Q在一行里按递增的顺序输出LeleW一ơ可以加的h(hun)。两个数据之间用I格隔开?br>如果Lele在第一ơ无论如何出价都无法买到q块土地Q就输出"none"?br>
Sample Input
4 2
3 2
3 5
Sample Output
1
none
3 4 5
题目分析:
代码如下:
#include <iostream>
int main ()
{
int n,m;
while ( scanf ( "%d%d", &m, &n ) != EOF )
{
if ( m % ( n + 1 ) == 0 )
{
puts ( "none" );
}
else
{
if ( n >= m )
{
for ( int i = m; i <= n; ++ i )
{
printf ( i == m ? "%d" : " %d",i );
}
putchar ( '\n' );
}
else
{
printf ( "%d\n", m % ( n + 1 ) );
}
}
}
return 0;
}
]]>
题目地址:
http://acm.hdu.edu.cn/showproblem.php?pid=2188
题目描述:
Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1337 Accepted Submission(s): 716
Problem Description
对于四川同胞(yu)遭受的灾难，全国人民UL(fng)伸出援助之手Q几乎每个省市都zև了大量的救援人员Q这其中包括抢险救灾的武警部队，ȝ和防疫的L人员Q以及进行心理疏导的心理学专家。根据要求，我校也有一个奔赴灾区救灄名额Q由于广大师生报名踊跃，学校不得不进行选拔来决定最后的人选。经q多轮的考核QŞ劉K渐明朗Q最后的名额在“林队”?#8220;徐队”之间产生。但是很巧合Q?个h的简历几乎一模一Pq让L选拔?600很是为难。无奈，他决定通过捐款来决定两能入选?br>选拔规则如下Q?br>1、最初的捐款是I的Q?br>2、两捐ƾ，每次捐款额必Mؓ(f)正整敎ͼq且每h每次捐款最多不过m?1<=m<=10)?br>3、最先得LN辑ֈ或者超qn元（0<n<10000Q的一方ؓ(f)胜者，则其可以亲ʎ灑服务?br>我们知道Q两人都很想入选志愿者名单，q且都是非常聪明的hQ假设林队先捐，请你判断谁能入选最后的名单Q?br>
Input
输入数据首先包含一个正整数CQ表C包含Cl测试用例，然后是C行数据，每行包含两个正整数nQmQn和m的含义参见上面提到的规则?br>
Output
对于每组试数据Q如果林队能入选，误出字W串"Grass"Q?nbsp;如果徐队能入选，误出字W串"Rabbit"Q每个实例的输出占一行?br>
Sample Input
2
8 10
11 10
Sample Output
Grass
Rabbit
题目分析:
代码如下:
#include <iostream>
int main ()
{
int T;
scanf ( "%d",&T );
{
while ( T -- )
{
int n,m;
scanf ( "%d%d", &n, &m );
puts ( n % ( 1 + m ) != 0 ? "Grass" : "Rabbit" );
}
}
return 0;
}
]]>
题目地址:
http://acm.hdu.edu.cn/showproblem.php?pid=1847
题目描述:
大学p四考试p来(f)了，你是不是在紧张的复习(fn)Q也许紧张得q短学期的ACM都没工夫l习(fn)了，反正我知道的Kiki和Cici都是如此。当Ӟ作ؓ(f)在考场润了十几蝲的当代大学生QKiki和Cici更懂得考前的放松，所?#8220;张弛有道”是q个意思。这不，Kiki和Cici在每天晚上休息之前都要玩一?x)儿扑克牌以放松经?br>“升”Q?#8220;双扣”Q?#8220;U五”Q还?#8220;斗地?#8221;Q?br>当然都不是！那多俗啊~
作ؓ(f)计算机学院的学生QKiki和Cici打牌的时候可没忘C业，她们打牌的规则是q样的：(x)
1?nbsp; dn张牌;
2?nbsp; 双方轮流抓牌Q?br>3?nbsp; 每h每次抓牌的个数只能是2的幂ơ（卻I(x)1Q?/span>2Q?/span>4Q?/span>8Q?/span>16…Q?br>4?nbsp; 抓完牌，胜负l果也出来了Q最后抓完牌的h者；
假设Kiki和Cici都是_聪明Q其实不用假设，哪有不聪明的学生~Q，q且每次都是Kiki先抓牌，请问谁能赢呢Q?br>当然Q打牌无赢都问题不大Q重要的是马上到来的CET-4能有好的状态?br>
Good luck in CET-4 everybody!
Input
输入数据包含多个试用例Q每个测试用例占一行，包含一个整数nQ?/span>1<=n<=1000Q?br>
Output
如果Kiki能赢的话Q请输出“Kiki”Q否则请输出“Cici”Q每个实例的输出占一行?br>
Sample Input
1
3
Sample Output
Kiki
Cici
题目分析:
首先我们可以惛_在面?的时候是必|局Q谁面对3时无论拿多少都会(x)?! <---q是关键
那么p量造成q样的局势给Ҏ(gu)Q因ZQ何不?的倍数的数??都可以变?的倍数Q?br>同理减去1?也可以变?的倍数Q也是说假讄前的个数不是3的倍数Q那我肯定能把它
拿成3的倍数Q比如现在是11个，那我拿走2个就变成9Q这样就造成Ҏ(gu)?的倍数局势，?br>么对Ҏ(gu)m个我都可以通过?或?使d一轮拿的数目成?的倍数Q这样就?x)有两种情?
1.刚好拿完.
2.剩下的还?的倍数个，那l?
所以这h下去必胜
代码如下:
#include <iostream>
using namespace std;
int main ()
{
int N;
while ( cin >> N )
{
puts ( N % 3 != 0 ? "Kiki" : "Cici" );
}
return 0;
}
]]>
题目地址:
http://acm.hdu.edu.cn/showproblem.php?pid=1849
题目描述:
大学时光是浪漫的Q女生是O的，圣诞更是O的，但是Rabbit和Grassq两个大学女生在今年的圣诞节却表现得一炚w不浪漫：(x)不去逛商场，不去逛公园，不去和ACL(fng)?x)，两个人竟然猫在寝食下?#8230;…
说是下棋Q其实只是一个简单的游戏而已Q游戏的规则是这L(fng)Q?br>1?nbsp; 盘包含1*n个方|Ҏ(gu)从左到右分别~号?Q?/span>1Q?/span>2Q?#8230;Qn-1Q?br>2?nbsp; m个棋子放在棋盘的Ҏ(gu)上，Ҏ(gu)可以为空Q也可以攑֤于一个的子Q?br>3?nbsp; 双方轮流走棋Q?br>4?nbsp; 每一步可以选择L一个棋子向左移动到L的位|（可以多个子位于同一个方|Q当ӞM子不能出盘边界Q?br>5?nbsp; 如果所有的子都位于最左边Q即~号?的位|）Q则游戏l束Qƈ且规定最后走的一方ؓ(f)胜者?br>
对于本题Q你不需要考虑n的大（我们可以假设在初始状态，子L位于盘的适当位置Q。下面的C意囑֍Z?*15的棋盘，共有6个棋子，其中Q编?的位|有两个子?br>
大家知道Q虽然偶?dng)不够浪漫，但是Rabbit和Grass都是冰雪聪明的女生，如果每次都是Rabbit先走，误出最后的l果?br>
Input
输入数据包含多组试用例Q每个测试用例占二行Q首先一行包含一个整数mQ?/span>0<=m<=1000Q，表示本测试用例的子数目Q紧跟着的一行包含m个整数Ki(i=1…m; 0<=Ki<=1000)Q分别表Cm个棋子初始的位置Qm=0则结束输入?br>
Output
如果Rabbit能赢的话Q请输出“Rabbit Win!”Q否则请输出“Grass Win!”Q每个实例的输出占一行?br>
Sample Input
2
3 5
3
3 5 6
0
Sample Output
Rabbit Win!
Grass Win!
题目分析 :
标准 ?nim 博弈 问题, 不要惛_杂了 . 因ؓ(f)只能往左移, 所以可以将 初始的每个棋子的位置看成一个堆, 比如? 1个棋子在 n-1? 那么׃表这个堆?n-1个数
左移1?是取走一? 所以有 m 子׃表有m个堆, 全部?是取完?........... 更具体的 nim 博弈介绍L(fng)?nbsp; << 博弈入门 >>
代码如下:
#include <iostream>
int heap[1001];
int main ()
{
int T;
while ( scanf ( "%d",&T ), T )
{
int res = 0 , nCount = 0;
for ( int i = 0; i != T; ++ i )
{
scanf ( "%d",heap + i );
res ^= heap[i];
}
puts ( res == 0 ? "Grass Win!" : "Rabbit Win!" );
}
return 0;
}
]]>
题目地址:
http://acm.hdu.edu.cn/showproblem.php?pid=1846
题目描述:
十年前读大学的时候，中国每年都要从国外引q一些电(sh)影大片，其中有一部电(sh)影就叫《勇敢者的游戏》（英文名称QZathuraQ，一直到现在Q我依然对于?sh)媄中的部分电(sh)脑?gu)印象深刻?br>今天Q大安择上机考试Q就是一U勇敢（braveQ的选择Q这个短学期Q我们讲的是博弈QgameQ专题；所以，大家现在玩的也是“勇敢者的游戏”Q这也是我命名这个题目的原因?br>当然Q除?#8220;勇敢”Q我q希望看?#8220;诚信”Q无试成W如何Q希望看到的都是一个真实的l果Q我也相信大家一定能做到?/span>~
各位勇敢者要玩的W一个游戏是什么呢Q很单，它是q样定义的：(x)
1?nbsp; 本游戏是一个二人游?
2?nbsp; 有一堆石子一共有n个；
3?nbsp; 两h轮流q行;
4?nbsp; 每走一步可以取?…m个石子；
5?nbsp; 最先取光石子的一方ؓ(f)胜；
如果游戏的双方用的都是最优策略，误出哪个h能赢?br>
Input
输入数据首先包含一个正整数C(C<=100)Q表C有Cl测试数据?br>每组试数据占一行，包含两个整数n和mQ?/span>1<=n,m<=1000Q，n和m的含义见题目描述?br>
Output
如果先走的h能赢Q请输出“first”Q否则请输出“second”Q每个实例的输出占一行?br>
Sample Input
2
23 2
4 3
Sample Output
first
second
题目分析:
巴什博弈Q一个h?～m个，那谁面对m+1的局势的的时候则必|Q很明显Q先拿的是要造这个局?如果n?m+1)*r+s(kZQ意，s<m+1),那么很明昑օ拿的拿掉s后，然后无论下一个拿多少你都可以保证你拿完后都是拿了m+1个，q样后拿的必定面对必败局势，比如23 2Q?3=Q?×7Q?2Q那我第一ơ拿?Q然后无论每ơ第二个拿几我都可以使得q轮d?Q然后他必定?x)面?q个局势，然后我就必胜Q那什么时候必败呢Q很明显如果我面对的是（m+1Q的倍数的局势就必|?br>puts ( n % ( 1 + m ) != 0 ? "first" : "second" );
l果竟然被这题给阴了....while(scanf("%d",&c)!=EOF) --> l果WA, YM
然后Ҏ(gu) scanf("%d",&c) 居然 AC ? ...................(zhn)剧～～?/p>
代码如下 :
#include <iostream>
int main ()
{
int T;
scanf ( "%d",&T );
{
while ( T -- )
{
int n,m;
scanf ( "%d%d", &n, &m );
puts ( n % ( 1 + m ) != 0 ? "first" : "second" );
}
}
return 0;
}
]]>
题目地址:
http://acm.hdu.edu.cn/showproblem.php?pid=1850
题目描述:
一q在?nbsp;父母时刻牉|
春节回家 你能做几天好孩子?br>寒假里尝试做做下面的事情?br>
陪妈妈逛一ơ菜?br>(zhn)?zhn)l爸怹个小C物
d?nbsp;强烈?nbsp;要求z一ơ碗
某一天早?nbsp;l爸妈用心地做回早餐
如果愿意 你还可以和爸妈说
׃玩个游戏吧 ACM课上学的呢～
下面是一个二人小游戏Q桌子上有M堆扑克牌Q每堆牌的数量分别ؓ(f)Ni(i=1…M)Q两进行；每走一步可以Q意选择一堆ƈ取走其中的Q意张牌；桌子上的扑克全部取光Q则游戏l束Q最后一ơ取牌的Zؓ(f)胜者?br>现在我们不想研究到底先手q是Q我只想问大Ӟ(x)
—?#8220;先手的h如果惌Q第一步有几种选择呢？”
Input
输入数据包含多个试用例Q每个测试用例占2行，首先一行包含一个整数M(1<M<100)Q表C扑克牌的堆敎ͼ紧接着一行包含M个整数Ni(1<=Ni<=1000000Qi=1…M)Q分别表CM堆扑克的数量。M?则表C入数据的l束?br>
Output
如果先手的h能赢Q请输出他第一步可行的Ҏ(gu)敎ͼ否则误?Q每个实例的输出占一行?br>
Sample Input
3
5 7 9
0
Sample Output
1
题目分析 :
MiYu原创, 转帖h?: 转蝲?______________白白の屋
一.
如果a1^a2^a3^...^an=0 ( ?: nim-sum=0 ) , 说明先手没有必赢{略, Ҏ(gu)数肯定ؓ(f) 0;
?
假设先手的h有必赢策略?/p>
问题则{化ؓ(f)=>在Q意一堆拿LK张牌Qƈ且剩下所有堆的nim-sum=0(P-position)的方案L?/p>
1. 现在我们先看一个例?5,7,9)Qƈ假设从第一堆取LK张牌?/p>
排除W一堆牌的nim-sum?7^9=14
0111
^1001
-------
1110
如果要所有堆的nim-sum=0成立Q则W一堆取掉K张以后必定ؓ(f)1110Q因为X^X=0?/p>
所以要观察 5-k=14 k>0 成立,此例?在第一堆取LK张牌)明显的不成立。但q不代表在第二或W三堆取LK张牌的解不成立?/p>
2. 现在看第二个例子(15,7,9)Qƈ假设从第一堆取LK张牌?/p>
排队W一堆牌的nim-sum?^9=14Q和W一个例子相同，所以问题变?15-k=14 k>0 是否成立?/p>
当然q个例子是成立的?/p>
?
ȝ得出Q?/p>
在Q意一堆拿LK张牌Qƈ且所有堆的nim-sum=0 成立的条件ؓ(f)Q排除取掉K张牌的那一堆的nim-sum必须于该堆牌上的数?例子?Q否则不能在此堆上取LK张牌使所有堆的nim-sum=0成立(例子一)?/p>
故L案数?( 在Q意一堆拿LK张牌Qƈ且所有堆的nim-sum=0 成立 ) 的L?/p>
代码如下 :
#include <iostream>
int heap[101];
int main ()
{
int T;
while ( scanf ( "%d",&T ), T )
{
int res = 0 , nCount = 0;
for ( int i = 0; i != T; ++ i )
{
scanf ( "%d",heap + i );
res ^= heap[i];
}
if ( res == 0 )
{
puts ( "0" );
continue;
}
int cmp = 0;
for ( int i = 0; i != T; ++ i )
{
cmp = res ^ heap[i];
if ( cmp < heap[i] )
{
nCount ++;
}
}
printf ( "%d\n",nCount );
}
return 0;
}
]]>
题目地址:
http://acm.hdu.edu.cn/showproblem.php?pid=2897
题目描述:
当日遇到月，于是有了明。当我遇C你，便成了G?br>那天Q日月相?x)，我见C你。而且Q大地失M光辉Q你我是否成侣？q注定是个凄的故事。（以上是废话）
t和所有世俗的Z一P期待那百q难遇的日食。驻头看天，看日月渐渐走q，t的脖子那个酸呀Q他坚持q个姿势已经有半个多时啦）。他低下仰v的头Q环֛周。忽然发现n边竟站着位漂亮的mm。天渐渐暗下Q这mm在这街头竟然如此耀|Ҏ(gu)天吗？站着tw边的天ѝ?br>t对mm惊呼Q?#8220;~分?/span>~~”。mm却毫不含p：(x)“是啊Q?00q一遇哦Q?#8221;Q此后省?000?#8230;.Q?br>t赶紧向mm要联pL式，可mm_(d)(x)“我和你玩个游戏吧Q赢了，我就把我的手机号告诉你?#8221;tQ心惛_下哪有题目能隑ր我呢，便满口答应下来。mm开始说游戏规则Q?#8220;我有一堆硬币，一?枚，从这个硬币堆里取币Q一ơ最取2枚，最?枚，如果剩下于2枚就要一ơ取完。我和你轮流取，直到堆里的硬币取完，最后一ơ取币的算输。我玩过q个游戏好多ơ了Q就让让你，让你先取?/span>~”
t掐指一，不对呀Q这是不可能的Q务么。小t露出得意的笑Q?#8220;q是mm优先啦，呵呵~”mm霎时愣住了，x对小t的反应出乎意料吧?br>她却也不生气Q?#8220;好小子，明呢Q要不这样吧Q你把我的邮q我，我给你发个文本，每行有三个数字nQpQqQ表CZ堆硬币一共有n枚，从这个硬币堆里取币Q一ơ最取p枚，最多q枚，如果剩下于p枚就要一ơ取完。两取Q直到堆里的币取完Q最后一ơ取币的算输。对于每一行的三个数字Q给出先取的人是否有必胜{略Q如果有回答WINQ否则回{LOST。你把对应的{案发给我，如果你能在今天晚?点以前发l我正确{案Q或许我们明天下午可以再见?#8221;
t二话没说Q将自己的邮q了mm。当他兴冲冲得赶回家Q上|看邮箱Q哇Qmm的邮件已l到了。他发现文本长达100000行，每行的三个数字都很大Q但是都是不过65536的整数。小t看表已经下午6点了Q要x工算出所有结果，看来是不可能了。你能帮帮他Q让他再见到那个mm吗？
Input
不超q?00000行，每行三个正整数nQpQq?br>
Output
对应每行输入Q按前面介绍的游戏规则，判断先取者是否有必胜{略。输出WIN或者LOST?br>
Sample Input
7 2 4
6 2 4
Sample Output
LOST
WIN
博弈的入门题, 巴什博奕(Bash Game), 具体了解L(fng)?nbsp; 博弈入门 .
代码如下:
#include <iostream>
int main ()
{
int N, p, q;
while ( scanf ( "%d%d%d",&N, &p, &q ) != EOF )
{
int res = N % ( p + q );
puts ( res ? res <= p ? "LOST" : "WIN" : "WIN" );
}
return 0;
}
另外UU自己的一行代?:
main(p,q){int N,res;while(~scanf("%d%d%d",&N,&p,&q)){res=N%(p+q);puts(res?res<=p?"LOST":"WIN":"WIN");}}
]]>
Lq状态（也称必|态， 奇异局势）Q（满QQ意非q态经q一ơ操作可以变为^衡态）
(一)巴什博奕(Bash Game):
只有一?/span>n个物?/span>,两个从q堆物品中取?/span>,规定每次臛_取一?/span>,最多取m?/span>.最后取光者得?/span>.
n = (m+1)r+s , (rZQ意自然数,s≤m), ?/span>n%(m+1) != 0, 则先取者肯定获?/span>
(?/span>)威佐夫博?/span>(Wythoff Game):
有两堆各若干个物?/font>,两个从某一堆或同时从两堆中取同样多的物?/font>,规定每次臛_取一?/font>,多者不?/font>,最后取光者得?/font>.
(ak,bk)(ak ≤ bk ,k=0,1,2,...,n)表示奇异局?/span>
求法Q?/span>
ak =[k(1+√5)/2], bk= ak + k (k=0,1,2,...,n Ҏ(gu)可C取整函?/span>)
判断Q?/span>
Gold=(1+sqrt(5.0))/2.0Q?/span>
1Q假设（aQ?/span>bQؓ(f)W?/span>kU奇异局?/span>(k=0,1,2...) 那么k=b-a;
2Q判断其a==(int)(k*Gold),相等则ؓ(f)奇异局?/span>
Q注Q采用适当的方?/span>,可以非奇异局势变为奇异局?/span>.
假设面对的局势是(a,b)
?/span> b = a,则同时从两堆中取?/span> a 个物?/span>,变Z奇异局?/span>(0,0)Q?/span>
1. 如果a = ak,
1.1 b > bk, 那么,取走b - bk个物?/span>,卛_为奇异局?/span>(ak, bk)Q?/span>
1.2 b < bk 则同时从两堆中拿?/span> ak – a[b – ak]个物?/span>,变ؓ(f)奇异局?/span>( a[b – ak] , a[b – ak]+ b - ak)Q?/span>
2 如果a = bk ,
2.1 b > ak ,则从W二堆中拿走多余的数?/span>b – ak
2.2 b < ak ,?/span> ?/span>b = aj (j < k) 从第一堆中拿走多余的数?/span>a– bj; (a > bj)
?/span>b = bj (j < k) 从第一堆中拿走多余的数?/span>a– aj; ( a > aj)
Q?/span>
例题Q?/span>pku 1067
(?/span>)姆博奕(Nimm Game):
?/font>n堆各若干个物?/font>,两个从某一堆取L多的物品,规定每次臛_取一?/font>,多者不?/font>,最后取光者得?/font>.
M奇异局?/span>(a1, a2, … , an)都有a1(+)a2(+)…(+)an =0. ( (+)?/span> 按位^)
Nim游戏介：(x)
Q?Q有两个玩家Q?/p>
Q?Q有三堆扑克牌（比如Q可以分别是5Q?Q?张）Q?/p>
Q?Q玩家的每次操作是选择其中某一堆牌Q然后从中取CQ意张Q?/p>
nim游戏的定理一Q?/p>
对于nim游戏的某个位|?x1,x2,x3),当且仅当它各部分的nim-sum{于0Ӟ即x1⊕x2⊕x3=0Q（x1Qx2Qx3做异或操作^Q，则当前位于必败点?/p>
例题Q?/span>pku 2234 例题Q?/span>hdu 1730 例题Q?/span>pku 1740 例题Q?/span>pku 1704 例题Q?/span>pku 1082 (大量分析… l论很简单?/span> 也可以根据简单的推论模拟实现?/span>)
定义: 假设 (xm · · · x0)2 ?ym · · · y0)2 的nim-sum?zm · · · z0)2,则我们表C成 (xm · · · x0)2 ⊕ (ym · · · y0)2 = (zm · · · z0)2,
q里Qzk = xk + yk (mod 2)Qk=0…mQ?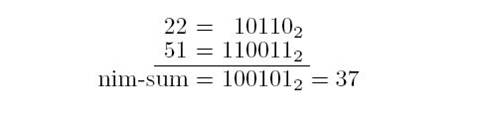 
]]>