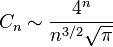ιΔ‰γ¦°ε€ΑεùÄ:
http://acm.hdu.edu.cn/showproblem.php?pid=2147
ιΔ‰γ¦°φèèηΩΑ:
Time Limit: 5000/1000 MS (Java/Others) Memory Limit: 40000/1000 K (Java/Others)
Total Submission(s): 1806 Accepted Submission(s): 1055
Problem Description
Recently kiki has nothing to do. While she is bored, an idea appears in his mind, she just playes the checkerboard game.The size of the chesserboard is n*m.First of all, a coin is placed in the top right corner(1,m). Each time one people can move the coin into the left, the underneath or the left-underneath blank space.The person who can't make a move will lose the game. kiki plays it with ZZ.The game always starts with kiki. If both play perfectly, who will win the game?
Input
Input contains multiple test cases. Each line contains two integer n, m (0<n,m<=2000). The input is terminated when n=0 and m=0.
Output
If kiki wins the game printf "Wonderful!", else "What a pity!".
Sample Input
5 3
5 4
6 6
0 0
Sample Output
What a pity!
Wonderful!
Wonderful!
ιΔ‰γ¦°εàÜφûê:
εàÜφûêεΠ²δΗ΄:
Pγ²ΙοΦöû°±φ‰·PδΗΣγü≥ε≠êγö³φ½ΕεÄôοΦ¨ε·“é•Ιφ΄Ωεè·δΜΞηΒΔ(η΅ΣεΖ±ηΨ™γö³)
Nγ²ΙοΦöû°±φ‰·NδΗΣγü≥ε≠êγö³φ½ΕεÄôοΦ¨η΅ΣεΖ±φ΄Ωεè·δΜΞηΒΔ
γéΑε€®εÖ≥δΚéP,Nγö³φ±²ηßΘφ€âδΗâδΗΣηß³εàô
εQ?εQâοΦöφ€ÄΨlàφĹιÉΫφ‰·P
εQ?εQâοΦöφ¨âγÖßφΗΗφàèηß³εàôεQ¨εàΑηΨë÷Ϋ™εâçφĹγö³εâçφĹιÉΫφ‰·Nγö³η·ùεQ¨εΫ™εâçφĹφ‰·P
εQ?εQâοΦöφ¨âγÖßφΗΗφàèηß³εàôεQ¨εàΑηΨë÷Ϋ™εâçφĹγö³εâçφĹη΅≥û°ëφ€âδΗÄδΗΣPγö³η·ùεQ¨εΫ™εâçφĹφ‰·N
ιΔ‰φ³èεQ?/p>
ε€®δΗÄδΗΣm*nγö³φȴ㦉εÜÖεQ¨δΜé(1,m)γ²Ιε΅ΚεèëοΦ¨φ·èφ§Γεè·δΜΞ‰q¦ηΓ¨γö³γßΜεä®φ‰·εQöεΖΠΩU÷MΗÄεQ¨δΗ΄ΩU÷MΗÄεQ¨εΖΠδΗ΄γßΜδΗÄψIJγ³Εεêékikiφ·èφ§ΓεÖàηΒΑεQ¨εàΛφ•≠kikiφ½ΕεÄôδΦöηΒΔοΦàε·“é•Ιφ½†ηΒ\εè·ηΒΑγö³φ½ΕεÄôοΦâψÄ?/p>
φàëδΜ§εè·δΜΞφääPNγäΕφĹγö³γ²“éèèΨl‰ε΅ΚφùΞοΦöεQ?/p>

‰qôδΚ¦γ²Ιγö³φèèγΜ‰φ€âδΗÄδΗΣγ®΄εΚèοΦöεQ?/p>
ψÄ?/p>
#include<iostream>
using namespace std;
bool map[2001][2001];//1 P 0 N;
int main(){
int i,j,k;
map[1][1]=1;
for(i=2;i<=2000;i++)
{
if(map[i-1][1])
map[i][1]=0;
else map[i][1]=1;
for(j=2;j<i;j++){
if(!map[i][j-1]&&!map[i-1][j-1]&&!map[i-1][j])
map[i][j]=1;
else map[i][j]=0;
}
if(map[1][i-1])
map[1][i]=0;
else map[1][i]=1;
for(j=2;j<i;j++){
if(!map[j-1][i]&&!map[j-1][i-1]&&!map[j][i-1])
map[j][i]=1;
else map[j][i]=0;
}
if(!map[i][i-1]&&!map[i-1][i-1]&&!map[i-1][i])
map[i][i]=1;
else map[i][i]=0;
}
int M,N;
for(i=1;i<=10;i++){
for(j=1;j<=10;j++)
printf("%c ",map[i][j]?'P':'N');
printf("\n");
}
while(scanf("%d%d",&M,&N)&&M&&N){
if(map[M][N]) printf("What a pity!\n");
else printf("Wonderful!\n");
}
return 0;
}
ψÄ?/p>
εÖΖδΫ™δΜΘγ†¹εΠ²δΗ΄:
using namespace std;
int main ()
{
int n,m;
while ( cin >> n >> m , n + m )
{
puts ( n%2 && m % 2 ? "What a pity!" : "Wonderful!");
}
return 0;
}
ιΔ‰γ¦°ε€ΑεùÄ:
http://acm.hdu.edu.cn/showproblem.php?pid=2149
ιΔ‰γ¦°φèèηΩΑ:
Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 719 Accepted Submission(s): 419
Problem Description
ηôΫγ³ΕδΗçφÉ≥εQ¨δΫÜφ‰·γéΑε°ûφÄ’dΫ£φ‰·γéΑε°ûοΦ¨Leleεß΄γΜàφ≤Γφ€âιÄÉηΩ΅ιÄÄε≠Πγö³εëΫηΩêεQ¨ε¦†δΗόZΜ•φ≤Γφ€âφ΄ΩεàΑεΞ•ε≠Πι΅ëψIJγéΑε€®γ≠âεΨÖδΜ•γö³οΦ¨û°±φ‰·εÉèFarmJohnδΗÄφ†οLö³εÜ€γîΑγîüφ³”ψÄ?br>
ηΠ¹γßçγîΑεΨ½φ€âγîΑφâçηΓ¨εQ¨Leleεê§η·¥ηΓ½δΗäφ≠Θε€®δΗΨηΓ¨δΗÄε€ΚεàΪεΦÄγîüιùΔγö³φ΄çεç•δΦöεQ¨φ΄çεç•γö³γâ©ε™¹φ≠ΘεΞΫû°±φ‰·δΗÄεù?0δΚ©γö³γîΑε€ΑψIJδΚéφ‰·οΦ¨LeleεΗΠδΗäδΜ•γö³εÖ®ιÉ®ΩU·η™³εQ¨εÜ≤εΨÄφ΄çεç•δΦöψÄ?br>
εêéφùΞεèëγéΑεQ¨φï¥δΗΣφ΄çεç•δΦöεèΣφ€âLele壨δΜ•γö³φ≠Με·ΙεΛ¥YueyueψÄ?br>
ιÄöηΩ΅φâ™εê§εQ¨LeleγüΞι¹™‰qôε€Κφ΄çεç•γö³ηß³εàôφ‰·‰qôφ†Ζγö³οΦöεàöεΦÄεß΄εΚïδΜΖδΊ™0εQ¨δΗΛδΗΣδùhηΫ°φΒ¹εΦÄεß΄εä†δΜχPΦ¨δΗçηΩ΅φ·èφ§Γεä†δ≠hγö³εΙÖεΚΠηΠ¹ε€?οΫûNδΙ΄ι½¥εQ¨εΫ™δΜδh†ΦεΛßδΚéφà•γ≠âδΚéγîΑε€Αγö³φàêφ€§δΜ?nbsp;M φ½”ûΦ¨δΗ’däûφ•ΙεΑ±φääηΩôεù½γîΑε€Αεç•ΨlôηΩô΄ΤΓεèΪδΜοLö³δΚΚψÄ?br>
Lele壨YueyueηôΫγ³ΕηÄÉη·ïδΗçηΓ¨εQ¨δΫÜφ‰·ε·Ιφ΄çεç•εç¥εç¹εàÜγ≤ΨιÄöοΦ¨ηĨδΗîδΜ•δΜ§δΗΛδΗΣδΚΚιÉΫεç¹εàÜφɦ_Ψ½εàΑηΩôεù½γîΑε€ΑψIJφâÄδΜΞδΜ•δΜ§φ·è΄ΤΓιÉΫφ‰·ιÄâε·Ιη΅ΣεΖ±φ€Äφ€âεà©γö³φ•ΙεΦèηΩ¦ηΓ¨εä†δΜ½ςÄ?br>
γîΉÉΚéLeleε≠½εÖΗεΚèφ·îYueyueιù†εâçεQ¨φâÄδΜΞφ·è΄ΤΓιÉΫφ‰·γî±LeleεÖàεΦÄεß΄εä†δΜχPΦ¨η·Ζι½°εQ¨γ§§δΗÄ΄ΤΓεä†δΜοLö³φ½ΕεÄôοΦ¨
LeleηΠ¹ε΅ΚεΛöεΑëφâçηÉΫδΩùη·¹η΅ΣεΖ±δΙΑεΨ½εàΑηΩôεù½ε€ΑεëΔοΦü
Input
φ€§ιΔ‰γ¦°ε¨ÖεêΪεΛöΨl³φΒ΄η·ïοΦ¨η·ΖεΛ³γêÜεàΑφ•΅δögΨl™φùü(EOF)ψIJφ·èΨl³φΒ΄η·ïεç†δΗÄηΓ¨ψÄ?br>φ·èγΜ³΄Ι΄η·ïε¨ÖεêΪδΗΛδΗΣφï¥φïΑM壨N(εêΪδΙâηß¹ιΔ‰γ¦°φèè‰qéΆΦ¨0<NεQ¨M<1100)
Output
ε·ΙδΚéφ·èγΜ³φïΑφç°εQ¨ε€®δΗÄηè顨φ¨âιÄ£εΔûγö³ιΓΚεΚèηΨ™ε΅ΚLeleΫW§δΗÄ΄ΤΓεè·δΜΞεä†γö³δ≠hψIJδΗΛδΗΣφïΑφç°δΙ΄ι½¥γî®ΫIΚφ†ΦιöîεΦÄψÄ?br>εΠ²φû€Lele倮㧧δΗÄ΄ΤΓφ½†η°ΚεΠ²δΫïε΅ΚδΜΖιÉΫφ½†φ≥ïδΙΑεàΑ‰qôεù½ε€üε€ΑεQ¨εΑ±ηΨ™ε΅Κ"none"ψÄ?br>
Sample Input
4 2
3 2
3 5
Sample Output
1
none
3 4 5
ιΔ‰γ¦°εàÜφûê:
δΜΘγ†¹εΠ²δΗ΄:
#include <iostream>
int main ()
{
int n,m;
while ( scanf ( "%d%d", &m, &n ) != EOF )
{
if ( m % ( n + 1 ) == 0 )
{
puts ( "none" );
}
else
{
if ( n >= m )
{
for ( int i = m; i <= n; ++ i )
{
printf ( i == m ? "%d" : " %d",i );
}
putchar ( '\n' );
}
else
{
printf ( "%d\n", m % ( n + 1 ) );
}
}
}
return 0;
}
ιΔ‰γ¦°ε€ΑεùÄ:
http://acm.hdu.edu.cn/showproblem.php?pid=2188
ιΔ‰γ¦°φèèηΩΑ:
Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1337 Accepted Submission(s): 716
Problem Description
ε·ΙδΚé妦εΖùεê¨ηÉûι¹≠εè½γö³γ¹ΨιöΨοΦ¨εÖ®ε¦ΫδΚΚφΑëΨUοLΚΖδΦΗε΅Κφè¥εä©δΙ΄φâ΄εQ¨ε΅†δΙéφ·èδΗΣγ€¹εΗ²ιÉΫ΄zë÷΅ΚδΚÜεΛßι΅èγö³φïëφè¥δΚΚεë‰εQ¨ηΩôεÖΕδΗ≠ε¨Öφ΄§φäΔιô©φïëγ¹Ψγö³φ≠Πη≠ΠιÉ®ι‰üοΦ¨φ≤»ù•½ε£¨ι‰≤γ•Ϊγö³ε¨άLäΛδΚΚεë‰εQ¨δΜΞεèäηΩ¦ηΓ¨εΩÉγêÜγ•èε·Φγö³εΩÉγêÜε≠ΠδΗ™ε°ΕψIJφ†Ιφç°ηΠ¹φ±²οΦ¨φàëφ†ΓδΙüφ€âδΗÄδΗΣεΞîηΒ¥γ¹Ψε¨Κφïëγ¹³Γö³εêçιΔùεQ¨γî±δΚéεΙΩεΛßεΗàγîüφäΞεêçηΗäηΖÉοΦ¨ε≠Πφ†ΓδΗçεΨ½δΗçηΩ¦ηΓ¨ιÄâφ΄îφùΞεÜ≥ε°öφ€Äεêéγö³δΚΚιÄâψIJγΜè‰q΅εΛöηΫ°γö³ηÄÉφ†ΗεQ¨ε≈ûεäâKÄêφΗêφ‰éφ€½εQ¨φ€Äεêéγö³εêçιΔùû°Üε€®“φû½ι‰ü”ε£?#8220;εΨêι‰ü”δΙ΄ι½¥δΚßγîüψIJδΫÜφ‰·εΨàεΖßεêàεQ?δΗΣδùhγö³γ°ÄεéÜ塆δΙéδΗÄφ®ΓδΗÄφ†χPΦ¨‰qôη°©δΗάL¨¹ιÄâφ΄îγö?600εΨàφ‰·δΗΚιöΨψIJφ½†εΞàοΦ¨δΜ•εÜ≥ε°öιÄöηΩ΅φçêφ§ΨφùΞεÜ≥ε°öδΗΛδΚχôΑ¹ηÉΫεÖΞιÄâψÄ?br>ιÄâφ΄îηß³εàôεΠ²δΗ΄εQ?br>1ψĹφ€Äεàùγö³φçêφ§ΨΫé±φ‰·ΫIΚγö³εQ?br>2ψĹδΗΛδΚχôΫ°΄Ι¹φçê΄ΤΨοΦ¨φ·èφ§Γφçêφ§ΨιΔùεΩÖôε÷MΊ™φ≠Θφï¥φïéΆΦ¨ρqΕδΗîφ·èδùhφ·èφ§Γφçêφ§Ψφ€ÄεΛöδΗç≠ëÖηΩ΅mεÖ?1<=m<=10)ψÄ?br>3ψĹφ€ÄεÖàδ΄…εΨ½φÄάLçê΄ΤυNΔùηΨë÷àΑφà•ηÄÖηΕÖ‰q΅nεÖÉοΦà0<n<10000εQâγö³δΗÄφ•ΙδΊ™ηÉ€ηÄÖοΦ¨εàôεÖΕεè·δΜΞδΚ≤η éγ¹ë÷¨Κφ€çεäΓψÄ?br>φàëδΜ§γüΞι¹™εQ¨δΗΛδΚΚιÉΫεΨàφÉ≥εÖΞιÄâεΩ½φ³ΩηÄÖεêçεçïοΦ¨ρqΕδΗîιÉΫφ‰·ιùûεΗΗη¹Σφ‰éγö³δùhεQ¨ε¹΅η°Ψφû½ι‰üεÖàφçêοΦ¨η·ΖδΫ†εàΛφ•≠ηΑ¹ηÉΫεÖΞιÄâφ€Äεêéγö³εêçεçïεQ?br>
Input
ηΨ™εÖΞφïΑφç°ιΠ•εÖàε¨ÖεêΪδΗÄδΗΣφ≠Θφï¥φïΑCεQ¨ηΓ®ΫCΚε¨ÖεêΪCΨl³φΒ΄η·ïγî®δΨ΄οΦ¨γ³Εεêéφ‰·CηΓ¨φïΑφç°οΦ¨φ·èηΓ¨ε¨ÖεêΪδΗΛδΗΣφ≠Θφï¥φïΑnεQ¨mεQ¨n壨mγö³εêΪδΙâεè²ηß¹δΗäιùΔφèêεàΑγö³ηß³εàôψÄ?br>
Output
ε·ΙδΚéφ·èγΜ³΄Ι΄η·ïφïΑφç°εQ¨εΠ²φû€φû½ι‰üηÉΫεÖΞιÄâοΦ¨η··²Ψ™ε΅Κε≠½ΫWΠδΗ≤"Grass"εQ?nbsp;εΠ²φû€εΨêι‰üηÉΫεÖΞιÄâοΦ¨η··²Ψ™ε΅Κε≠½ΫWΠδΗ≤"Rabbit"εQ¨φ·èδΗΣε°ûδΨ΄γö³ηΨ™ε΅Κεç†δΗÄηΓ¨ψÄ?br>
Sample Input
2
8 10
11 10
Sample Output
Grass
Rabbit
ιΔ‰γ¦°εàÜφûê:
δΜΘγ†¹εΠ²δΗ΄:
#include <iostream>
int main ()
{
int T;
scanf ( "%d",&T );
{
while ( T -- )
{
int n,m;
scanf ( "%d%d", &n, &m );
puts ( n % ( 1 + m ) != 0 ? "Grass" : "Rabbit" );
}
}
return 0;
}
ιΔ‰γ¦°ε€ΑεùÄ:
http://acm.hdu.edu.cn/showproblem.php?pid=1847
ιΔ‰γ¦°φèèηΩΑ:
εΛßε≠Πη΄όp·≠妦γώîηÄÉη·ïû°όpΠ¹φùΞδèΆδΚÜοΦ¨δΫ†φ‰·δΗçφ‰·ε€®γ¥ßεΦ†γö³εΛçδΙ†εQüδΙüη°Ηγ¥ßεΦ†εΨ½‰qûγü≠ε≠Πφ€üγö³ACMιÉΫφ≤ΓεΖΞεΛΪΨlÉδΙ†δΚÜοΦ¨εèçφ≠ΘφàëγüΞι¹™γö³Kiki壨CiciιÉΫφ‰·εΠ²φ≠ΛψIJεΫ™γ³”ûΦ¨δΫ€δΊ™ε€®ηÄÉε€Κ΄ΙΗφΕΠδΚÜεç¹ε΅†ηù≤γö³εΫ™δΜΘεΛßε≠ΠγîüεQ¨Kiki壨Ciciφ¦¥φ΅²εΨ½ηÄÉεâçγö³φîΨφùΨοΦ¨φâÄηΑ?#8220;εΦ†εΦ¦φ€âι¹™”û°±φ‰·‰qôδΗΣφ³èφÄùψIJηΩôδΗçοΦ¨Kiki壨Ciciε€®φ·èεΛ©φôöδΗäδΦëφ¹·δΙ΄εâçιÉΫηΠ¹γé©δΗÄδΦöε³ΩφâëεÖ΄γâ¨δΜΞφîΨφùΨΦ€ûγΜèψÄ?br>“εç΅γώî”εQ?#8220;εè¨φâΘ”εQ?#8220;ΨUΔδΚî”εQüηΩ‰φ‰?#8220;φ•½ε€ΑδΗ?#8221;εQ?br>εΫ™γ³ΕιÉΫδΗçφ‰·οΦ¹ι²ΘεΛöδΩ½εïä~
δΫ€δΊ™η°Γγ°½φ€Κε≠ΠιôΔγö³ε≠ΠγîüεQ¨Kiki壨Ciciφâ™γâ¨γö³φ½ΕεÄôεè·φ≤ΓεΩ‰η°νCΗ™δΗöοΦ¨εΞΙδΜ§φâ™γâ¨γö³ηß³εàôφ‰·‰qôφ†Ζγö³οΦö
1ψÄ?nbsp; φÄ’dÖ±nεΦ†γâ¨;
2ψÄ?nbsp; εè¨φ•ΙηΫ°φΒ¹φä™γâ¨εQ?br>3ψÄ?nbsp; φ·èδùhφ·èφ§Γφä™γâ¨γö³δΗΣφïΑεèΣηÉΫφ‰·2γö³εΙ²΄ΤΓοΦàεçΜIΦö1εQ?/span>2εQ?/span>4εQ?/span>8εQ?/span>16…εQ?br>4ψÄ?nbsp; φä™ε°¨γâ¨οΦ¨ηÉ€η¥üΨl™φû€δΙüε΅ΚφùΞδΚÜεQöφ€Äεêéφä™ε°¨γâ¨γö³δùhδΗχôÉ€ηÄÖοΦ¦
ε¹΅η°ΨKiki壨CiciιÉΫφ‰·≠ë¦_Λüη¹Σφ‰éεQàεÖΕε°ûδΗçγî®ε¹΅η°ΨοΦ¨ε™Σφ€âδΗçη¹Σφ‰éγö³ε≠Πγîü~εQâοΦ¨ρqΕδΗîφ·èφ§ΓιÉΫφ‰·KikiεÖàφä™γâ¨οΦ¨η·Ζι½°ηΑ¹ηÉΫηΒΔεëΔεQ?br>εΫ™γ³ΕεQ¨φâ™γâ¨φ½†η°χôΑ¹ηΒΔιÉΫι½°ιΔ‰δΗçεΛßεQ¨ι΅çηΠ¹γö³φ‰·ι©§δΗäεàΑφùΞγö³CET-4ηÉΫφ€âεΞΫγö³γäΕφĹψÄ?br>
Good luck in CET-4 everybody!
Input
ηΨ™εÖΞφïΑφç°ε¨ÖεêΪεΛöδΗΣ΄Ι΄η·ïγî®δΨ΄εQ¨φ·èδΗΣφΒ΄η·ïγî®δΨ΄εç†δΗÄηΓ¨οΦ¨ε¨ÖεêΪδΗÄδΗΣφï¥φïΑnεQ?/span>1<=n<=1000εQâψÄ?br>
Output
εΠ²φû€KikiηÉΫηΒΔγö³η·ùεQ¨η·ΖηΨ™ε΅Κ“Kiki”εQ¨εêΠεàôη·ΖηΨ™ε΅Κ“Cici”εQ¨φ·èδΗΣε°ûδΨ΄γö³ηΨ™ε΅Κεç†δΗÄηΓ¨ψÄ?br>
Sample Input
1
3
Sample Output
Kiki
Cici
ιΔ‰γ¦°εàÜφûê:
ιΠ•εÖàφàëδΜ§εè·δΜΞφɦ_àΑε€®ιùΔε·?γö³φ½ΕεÄôφ‰·εΩÖη”|ε±ÄεQ¨ηΑ¹ιùΔε·Ι3φ½Εφ½†η°Κφ΄ΩεΛöεΑëιÉΫδΦöη¥?! <---‰qôφ‰·εÖ≥ιî°
ι²ΘδΙàû°όpΠ¹û°Ϋι΅èιĆφàê‰qôφ†Ζγö³ε±ÄεäΩγΜôε·“é•ΙεQ¨ε¦†δΗόZ™QδΫïδΗçφ‰?γö³εÄçφïΑγö³φïΑεä?φà?ιÉΫεè·δΜΞεè‰φà?γö³εÄçφïΑεQ?br>εê¨γêÜε΅èεéΜ1φà?δΙüεè·δΜΞεè‰φà?γö³εÄçφïΑεQ¨δΙüû°±φ‰·η·¥ε¹΅η°³Γ¦°εâçγö³δΗΣφïΑδΗçφ‰·3γö³εÄçφïΑεQ¨ι²Θφàëη²·ε°öηÉΫφääε°É
φ΄Ωφàê3γö³εÄçφïΑεQ¨φ·îεΠ²γéΑε€®φ‰·11δΗΣοΦ¨ι²Θφàëφ΄ΩηΒΑ2δΗΣεΑ±εè‰φàê9εQ¨ηΩôφ†ΖεΑ±ιĆφàêε·“é•ΙδΗ?γö³εÄçφïΑε±ÄεäΩοΦ¨ι²?br>δΙàε·Ιφ•“é΄ΩmδΗΣφàëιÉΫεè·δΜΞιÄöηΩ΅φ΄?φà•ηÄ?δΫΩφÄ’dÖ±δΗÄηΫ°φ΄Ωγö³φïΑγ¦°φàêδΗ?γö³εÄçφïΑεQ¨ηΩôφ†ΖεΑ±δΦöφ€âδΗΛγßçφÉÖεÜΒ:
1.εàöεΞΫφ΄Ωε°¨.
2.εâ©δΗ΄γö³ηΩ‰φ€?γö³εÄçφïΑδΗΣοΦ¨ι²ΘγëτΨl?
φâÄδΜΞηΩôφ†δh΄ΩδΗ΄εéΜεΩÖηÉ€
δΜΘγ†¹εΠ²δΗ΄:
#include <iostream>
using namespace std;
int main ()
{
int N;
while ( cin >> N )
{
puts ( N % 3 != 0 ? "Kiki" : "Cici" );
}
return 0;
}
ιΔ‰γ¦°ε€ΑεùÄ:
http://acm.hdu.edu.cn/showproblem.php?pid=1849
ιΔ‰γ¦°φèèηΩΑ:
εΛßε≠Πφ½ΕεÖâφ‰·φΒΣφΦΪγö³εQ¨εΞ≥γîüφ‰·΄ΙΣφ‰Oγö³οΦ¨ε€Θη·ûφ¦¥φ‰·΄ΙΣφ‰Oγö³οΦ¨δΫÜφ‰·Rabbit壨Grass‰qôδΗΛδΗΣεΛßε≠ΠεΞ≥γîüε€®δΜäεΙ¥γö³ε€Θη·ûηä²εç¥ηΓ®γéΑεΨ½δΗÄγ²öwÉΫδΗçφΒΣφΦΪοΦöδΗçεéΜιĦεïÜε€ΚοΦ¨δΗçεéΜιĦεÖ§ε¦≠οΦ¨δΗçεéΜ壨ACγîοLΚΠδΦöοΦ¨δΗΛδΗΣδΚΚγΪüγ³Εγ¨Ϊε€®ε·ùιΘüδΗ΄΄²?#8230;…
η·¥φ‰·δΗ΄φΘ΄εQ¨εÖΕε°ûεèΣφ‰·δΗÄδΗΣγ°Äεçïγö³û°èφΗΗφàèηĨεΖ≤εQ¨φΗΗφàèγö³ηß³εàôφ‰·ηΩôφ†οLö³εQ?br>1ψÄ?nbsp; ΄²΄γ¦‰ε¨ÖεêΪ1*nδΗΣφ•Ιφ†ϊ|Φ¨φ•“é†ΦδΜéεΖΠεàΑεè≥εàÜεàΪΨ~•εèΖδΗ?εQ?/span>1εQ?/span>2εQ?#8230;εQ¨n-1εQ?br>2ψÄ?nbsp; mδΗΣφΘ΄ε≠êφîΨε€®φȴ㦉γö³φ•“é†ΦδΗäοΦ¨φ•“é†Φεè·δΜΞδΗΚγ©ΚεQ¨δΙüεè·δΜΞφîë÷ΛöδΚéδΗÄδΗΣγö³΄²΄ε≠êεQ?br>3ψÄ?nbsp; εè¨φ•ΙηΫ°φΒ¹ηΒΑφΘ΄εQ?br>4ψÄ?nbsp; φ·èδΗÄφ≠Ξεè·δΜΞιÄâφ΄©δΜάL³èδΗÄδΗΣφΘ΄ε≠êεêëεΖΠγßΜεä®εàΑδΜάL³èγö³δΫçΨ|°οΦàεè·δΜΞεΛöδΗΣ΄²΄ε≠êδΫçδΚéεê¨δΗÄδΗΣφ•Ιφ†ϊ|ΦâεQ¨εΫ™γ³”ûΦ¨δΜ÷MΫï΄²΄ε≠êδΗçηÉΫ≠ëÖε΅Κ΄²΄γ¦‰ηΨΙγï¨εQ?br>5ψÄ?nbsp; εΠ²φû€φâÄφ€âγö³΄²΄ε≠êιÉΫδΫçδΚéφ€ÄεΖΠηΨΙεQàεç≥Ψ~•εèΖδΗ?γö³δΫçΨ|°οΦâεQ¨εàôφΗΗφàèΨl™φùüεQ¨εΤàδΗîηß³ε°öφ€ÄεêéηΒΑ΄²΄γö³δΗÄφ•ΙδΊ™ηÉ€ηÄÖψÄ?br>
ε·ΙδΚéφ€§ιΔ‰εQ¨δΫ†δΗçι€ÄηΠ¹ηÄÉηôënγö³εΛßû°èοΦàφàëδΜ§εè·δΜΞε¹΅η°Ψε€®εàùεß΄γäΕφĹοΦ¨΄²΄ε≠êφÄάL‰·δΫçδΚé΄²΄γ¦‰γö³ιIJεΫ™δΫçγΫ°εQâψIJδΗ΄ιùΔγö³ΫCΚφ³èε¦ë÷ç≥δΗόZΗÄδΗ?*15γö³φȴ㦉οΦ¨εÖ±φ€â6δΗΣφΘ΄ε≠êοΦ¨εÖΕδΗ≠εQ¨γΦ•εè?γö³δΫçΨ|°φ€âδΗΛδΗΣ΄²΄ε≠êψÄ?br>

εΛßε°ΕγüΞι¹™εQ¨ηôΫγ³Εε¹Εû°îδΗçεΛüφΒΣφΦΪοΦ¨δΫÜφ‰·Rabbit壨GrassιÉΫφ‰·εÜΑι¦Ση¹Σφ‰éγö³εΞ≥γîüοΦ¨εΠ²φû€φ·èφ§ΓιÉΫφ‰·RabbitεÖàηΒΑ΄²΄οΦ¨η··²Ψ™ε΅Κφ€Äεêéγö³Ψl™φû€ψÄ?br>
Input
ηΨ™εÖΞφïΑφç°ε¨ÖεêΪεΛöγΜ³΄Ι΄η·ïγî®δΨ΄εQ¨φ·èδΗΣφΒ΄η·ïγî®δΨ΄εç†δΚ¨ηΓ¨εQ¨ιΠ•εÖàδΗÄηΓ¨ε¨ÖεêΪδΗÄδΗΣφï¥φïΑmεQ?/span>0<=m<=1000εQâοΦ¨ηΓ®γΛΚφ€§φΒ΄η·ïγî®δΨ΄γö³΄²΄ε≠êφïΑγ¦°εQ¨γ¥ßηΖüγùÄγö³δΗÄηΓ¨ε¨ÖεêΪmδΗΣφï¥φïΑKi(i=1…m; 0<=Ki<=1000)εQ¨εàÜεàΪηΓ®ΫCΚmδΗΣφΘ΄ε≠êεàùεß΄γö³δΫçγΫ°εQ¨m=0εàôγΜ™φùüηΨ™εÖΞψÄ?br>
Output
εΠ²φû€RabbitηÉΫηΒΔγö³η·ùεQ¨η·ΖηΨ™ε΅Κ“Rabbit Win!”εQ¨εêΠεàôη·ΖηΨ™ε΅Κ“Grass Win!”εQ¨φ·èδΗΣε°ûδΨ΄γö³ηΨ™ε΅Κεç†δΗÄηΓ¨ψÄ?br>
Sample Input
2
3 5
3
3 5 6
0
Sample Output
Rabbit Win!
Grass Win!
ιΔ‰γ¦°εàÜφûê :
φ†΅ε΅Ü γö?nim εçöεΦà ι½°ιΔ‰, δΗçηΠ¹φɦ_Λçφù²δΚÜ . 妆亙εèΣηÉΫεΨÄεΖΠγßΜ, φâÄδΜΞεè·δΜΞεΑÜ εàùεß΄γö³φ·èδΗΣφΘ΄ε≠êγö³δΫçγ۰〴φàêδΗÄδΗΣε†Ü, φ·îεΠ²η·? 1δΗΣφΘ΄ε≠êε€® n-1φ†? ι²ΘδΙàû°ΉÉΜΘηΓ®ηΩôδΗΣε†Üφ€?n-1δΗΣφïΑ
εΖΠγßΜ1φ†?û°±φ‰·εè•ηΒΑδΗÄδΗ? φâÄδΜΞφ€â m ΄²΄ε≠êû°ΉÉΜΘηΓ®φ€âmδΗΣε†Ü, εÖ®ιÉ®εà?û°±φ‰·εè•ε°¨δΚ?........... φ¦¥εÖΖδΫ™γö³ nim εçöεΦàδΜ΄γΜçη·οL²Ιε΅?nbsp; << εçöεΦàεÖΞι½® >>
δΜΘγ†¹εΠ²δΗ΄:
#include <iostream>
int heap[1001];
int main ()
{
int T;
while ( scanf ( "%d",&T ), T )
{
int res = 0 , nCount = 0;
for ( int i = 0; i != T; ++ i )
{
scanf ( "%d",heap + i );
res ^= heap[i];
}
puts ( res == 0 ? "Grass Win!" : "Rabbit Win!" );
}
return 0;
}
ιΔ‰γ¦°ε€ΑεùÄ:
http://acm.hdu.edu.cn/showproblem.php?pid=1846
ιΔ‰γ¦°φèèηΩΑ:
εç¹εΙ¥εâçη·ΜεΛßε≠Πγö³φ½ΕεÄôοΦ¨δΗ≠ε¦Ϋφ·èεΙ¥ιÉΫηΠ¹δΜéε¦ΫεΛ•εΦï‰q¦δΗÄδΚ¦γîΒεΫ±εΛßγâ΅οΦ¨εÖΕδΗ≠φ€âδΗÄιÉ®γîΒεΫ±εΑ±εèΪψÄäε΄΅φïΔηÄÖγö³φΗΗφàèψÄ΄οΦàη΄±φ•΅εêçγßΑεQöZathuraεQâοΦ¨δΗÄ㦥εàΑγéΑε€®εQ¨φàëδΨùγ³Εε·ΙδΚéγîΒεΣ³δΗ≠γö³ιÉ®εàÜγîΒη³ëγâ“éäÄεçΑη±ΓφΖ±εàΜψÄ?br>δΜäεΛ©εQ¨εΛßε°âôÄâφ΄©δΗäφ€ΚηÄÉη·ïεQ¨εΑ±φ‰·δΗÄΩUçε΄΅φïΔοΦàbraveεQâγö³ιÄâφ΄©εQ¦ηΩôδΗΣγü≠ε≠Πφ€üεQ¨φàëδΜ§η°≤γö³φ‰·εçöεΦàεQàgameεQâδΗ™ιΔ‰οΦ¦φâÄδΜΞοΦ¨εΛßε°ΕγéΑε€®γé©γö³δΙüφ‰·“ε΄΅φïΔηÄÖγö³φΗΗφàè”εQ¨ηΩôδΙüφ‰·φàëεëΫεêçηΩôδΗΣιΔ‰γ¦°γö³εéü妆ψÄ?br>εΫ™γ³ΕεQ¨ιôΛδΚ?#8220;ε΄΅φïΔ”εQ¨φàë‰q‰εΗ¨φ€¦γ€΄εà?#8220;η·öδΩΓ”εQ¨φ½†η°χôÄÉη·ïφàêγ΅WεΠ²δΫïεQ¨εΗ¨φ€¦γ€΄εàΑγö³ιÉΫφ‰·δΗÄδΗΣγ€üε°ûγö³Ψl™φû€εQ¨φàëδΙüγ¦ΗδΩΓεΛßε°ΕδΗÄε°öηÉΫε¹öεàΑγö?/span>~
εê³δΫçε΄΅φïΔηÄÖηΠ¹γé©γö³ΫW§δΗÄδΗΣφΗΗφàèφ‰·δΜÄδΙàεëΔεQüεΨàΫéÄεçïοΦ¨ε°Éφ‰·‰qôφ†Ζε°öδΙâγö³οΦö
1ψÄ?nbsp; φ€§φΗΗφàèφ‰·δΗÄδΗΣδΚ¨δΚΚφΗΗφà?
2ψÄ?nbsp; φ€âδΗÄε†Üγü≥ε≠êδΗÄεÖ±φ€ânδΗΣοΦ¦
3ψÄ?nbsp; δΗΛδùhηΫ°φΒ¹‰q¦ηΓ¨;
4ψÄ?nbsp; φ·èηΒΑδΗÄφ≠Ξεè·δΜΞεè•ηΒ?…mδΗΣγü≥ε≠êοΦ¦
5ψÄ?nbsp; φ€ÄεÖàεè•εÖâγü≥ε≠êγö³δΗÄφ•ΙδΊ™ηÉ€οΦ¦
εΠ²φû€φΗΗφàèγö³εè¨φ•Ιδ΄…γî®γö³ιÉΫφ‰·φ€ÄδΦ‰γ≠•γïΞοΦ¨η··²Ψ™ε΅Κε™ΣδΗΣδùhηÉΫηΒΔψÄ?br>
Input
ηΨ™εÖΞφïΑφç°ιΠ•εÖàε¨ÖεêΪδΗÄδΗΣφ≠Θφï¥φïΑC(C<=100)εQ¨ηΓ®ΫCΚφ€âCΨl³φΒ΄η·ïφïΑφç°ψÄ?br>φ·èγΜ³΄Ι΄η·ïφïΑφç°εç†δΗÄηΓ¨οΦ¨ε¨ÖεêΪδΗΛδΗΣφï¥φïΑn壨mεQ?/span>1<=n,m<=1000εQâοΦ¨n壨mγö³εêΪδΙâηß¹ιΔ‰γ¦°φèèηΩΑψÄ?br>
Output
εΠ²φû€εÖàηΒΑγö³δùhηÉΫηΒΔεQ¨η·ΖηΨ™ε΅Κ“first”εQ¨εêΠεàôη·ΖηΨ™ε΅Κ“second”εQ¨φ·èδΗΣε°ûδΨ΄γö³ηΨ™ε΅Κεç†δΗÄηΓ¨ψÄ?br>
Sample Input
2
23 2
4 3
Sample Output
first
second
ιΔ‰γ¦°εàÜφûê:
εΖ¥δΜÄεçöεΦàεQ¨δΗÄδΗΣδùhφ΄?οΫûmδΗΣοΦ¨ι²ΘηΑ¹ιùΔε·Ιm+1γö³ε±ÄεäΩγö³γö³φ½ΕεÄôεàôεΩÖη”|εQ¨εΨàφ‰éφ‰ΨεQ¨εÖàφ΄Ωγö³û°±φ‰·ηΠ¹ιĆηΩôδΗΣε±Äεä?εΠ²φû€nφ‰?m+1)*r+s(kδΗόZ™Qφ³èοΦ¨s<m+1),ι²ΘδΙàεΨàφ‰éφ‰ë÷Öàφ΄Ωγö³φ΄ΩφéâsεêéοΦ¨γ³Εεêéφ½†η°ΚδΗ΄δΗÄδΗΣφ΄ΩεΛöεΑëδΫ†ιÉΫεè·δΜΞδΩùη·¹δΫ†φ΄Ωε°¨εêéιÉΫφ‰·φ΄ΩδΚÜm+1δΗΣοΦ¨‰qôφ†Ζεêéφ΄Ωγö³εΩÖε°öιùΔε·ΙεΩÖη¥Ξε±ÄεäΩοΦ¨φ·îεΠ²23 2εQ?3=εQ?×7εQ?2εQ¦ι²Θφàë㧧δΗÄ΄ΤΓφ΄Ωφé?εQ¨γ³Εεêéφ½†η°Κφ·è΄ΤΓ㧧δΚ¨δΗΣφ΄Ω塆φàëιÉΫεè·δΜΞδΫΩεΨ½‰qôηΫ°φÄ’dÖ±φ΄?εQ¨γ³ΕεêéδΜ•εΩÖε°öδΦöιùΔε·?‰qôδΗΣε±ÄεäΩοΦ¨γ³ΕεêéφàëεΑ±εΩÖηÉ€εQ¨ι²ΘδΜÄδΙàφ½ΕεÄôεΩÖη¥ΞεëΔεQ¨εΨàφ‰éφ‰ΨεΠ²φû€φàëιùΔε·Ιγö³φ‰·οΦàm+1εQâγö³εÄçφïΑγö³ε±ÄεäΩεΑ±εΩÖη”|ψÄ?br>puts ( n % ( 1 + m ) != 0 ? "first" : "second" );
Ψl™φû€γΪüγ³ΕηΔΪηΩôιΔ‰γΜô鉥δΚÜ....while(scanf("%d",&c)!=EOF) --> Ψl™φû€WA, YM
γ³Εεêéφî“éàê scanf("%d",&c) ε±Öγ³Ε AC δΚ? ...................φ²≤εâßοΫûοΫûοΫ?/p>
δΜΘγ†¹εΠ²δΗ΄ :
#include <iostream>
int main ()
{
int T;
scanf ( "%d",&T );
{
while ( T -- )
{
int n,m;
scanf ( "%d%d", &n, &m );
puts ( n % ( 1 + m ) != 0 ? "first" : "second" );
}
}
return 0;
}
ιΔ‰γ¦°ε€ΑεùÄ:
http://acm.hdu.edu.cn/showproblem.php?pid=1850
ιΔ‰γ¦°φèèηΩΑ:
δΗÄρq¥ε€®εΛ?nbsp;γàΕφ·çφ½ΕεàΜγââ|¨²
φ‰Ξηä²ε¦ûε°Ε δΫ†ηÉΫε¹ö塆εΛ©εΞΫε≠©ε≠êεê?br>ε·£ε¹΅ι΅¨εΑùη·ïε¹öε¹öδΗ΄ιùΔγö³δΚ΄φÉÖεê?br>
ιôΣεΠàεΠàιĦδΗÄ΄ΤΓηè€ε€?br>φ²³φ²³ΨlôγàΗγàφÄΙΑδΗΣεΑèΫCΦγâ©
δΗ’dä®ε€?nbsp;εΦΚγÉàε€?nbsp;ηΠ¹φ±²΄z½δΗÄ΄ΤΓγΔ½
φüêδΗÄεΛ©φ½©ηΒ?nbsp;ΨlôγàΗεΠàγî®εΩÉε€Αε¹öε¦ûφ½©ιΛê
εΠ²φû€φ³Ωφ³è δΫ†ηΩ‰εè·δΜΞ壨γàΗεΠàη·¥
ε£ΉÉΜ§γé©δΗΣû°èφΗΗφàèεêß ACMη·ΨδΗäε≠Πγö³εëΔοΫû
δΗ΄ιùΔφ‰·δΗÄδΗΣδΚ¨δΚΚεΑèφΗΗφàèεQöφΓ¨ε≠êδΗäφ€âMε†ÜφâëεÖ΄γâ¨εQ¦φ·èε†Üγâ¨γö³φïΑι΅èεàÜεàΪδΊ™Ni(i=1…M)εQ¦δΗΛδΚχôΫ°΄Ι¹ηΩ¦ηΓ¨οΦ¦φ·èηΒΑδΗÄφ≠Ξεè·δΜΞδ™Qφ³èιÄâφ΄©δΗÄε†ÜεΤàεè•ηΒΑεÖΕδΗ≠γö³δ™Qφ³èεΦ†γâ¨οΦ¦φΓ¨ε≠êδΗäγö³φâëεÖ΄εÖ®ιÉ®εè•εÖâεQ¨εàôφΗΗφàèΨl™φùüεQ¦φ€ÄεêéδΗÄ΄ΤΓεè•γâ¨γö³δΚόZΊ™ηÉ€ηÄÖψÄ?br>γéΑε€®φàëδΜ§δΗçφÉ≥γ†îγ©ΕεàΑεΚïεÖàφâ΄δΗχôÉ€‰q‰φ‰·δΗχô¥üεQ¨φàëεèΣφÉ≥ι½°εΛßε°”ûΦö
βÄîβÄ?#8220;εÖàφâ΄γö³δùhεΠ²φû€φɨôΒΔεQ¨γ§§δΗÄφ≠Ξφ€â塆γßçιÄâφ΄©εëΔοΦü”
Input
ηΨ™εÖΞφïΑφç°ε¨ÖεêΪεΛöδΗΣ΄Ι΄η·ïγî®δΨ΄εQ¨φ·èδΗΣφΒ΄η·ïγî®δΨ΄εç†2ηΓ¨οΦ¨ιΠ•εÖàδΗÄηΓ¨ε¨ÖεêΪδΗÄδΗΣφï¥φïΑM(1<M<100)εQ¨ηΓ®ΫCΚφâëεÖ΄γâ¨γö³ε†ÜφïéΆΦ¨γ¥ßφéΞγùÄδΗÄηΓ¨ε¨ÖεêΪMδΗΣφï¥φïΑNi(1<=Ni<=1000000εQ¨i=1…M)εQ¨εàÜεàΪηΓ®ΫCΚMε†ÜφâëεÖ΄γö³φïΑι΅èψIJMδΗ?εàôηΓ®ΫCχôΨ™εÖΞφïΑφç°γö³Ψl™φùüψÄ?br>
Output
εΠ²φû€εÖàφâ΄γö³δùhηÉΫηΒΔεQ¨η·ΖηΨ™ε΅Κδ̕㧧δΗÄφ≠Ξεè·ηΓ¨γö³φ•“éΓàφïéΆΦ¨εêΠεàôη··²Ψ™ε΅?εQ¨φ·èδΗΣε°ûδΨ΄γö³ηΨ™ε΅Κεç†δΗÄηΓ¨ψÄ?br>
Sample Input
3
5 7 9
0
Sample Output
1
ιΔ‰γ¦°εàÜφûê :
MiYuεéüεà¦, ηΫ§εΗ•η·δh≥®φ‰?: ηΫ§ηù≤η΅?______________γôΫγôΫψ¹°ε±΄
δΗÄ.
εΠ²φû€a1^a2^a3^...^an=0 ( εç?: nim-sum=0 ) , η·¥φ‰éεÖàφâ΄φ≤Γφ€âεΩÖηΒΔΫ{•γïΞ, φ•“é≥ïφïΑη²·ε°öδΊ™ 0;
δΚ?
ε¹΅η°ΨεÖàφâ΄γö³δùhφ€âεΩÖηΒΔγ≠•γïΞψÄ?/p>
ι½°ιΔ‰εàôηù{娕亙=>ε€®δ™Qφ³èδΗÄε†Üφ΄ΩδΜάL³èKεΦ†γâ¨εQ¨εΤàδΗîεâ©δΗ΄φâÄφ€âε†Üγö³nim-sum=0(P-position)γö³φ•ΙφΓàφÄάLïΑψÄ?/p>
1. γéΑε€®φàëδΜ§εÖà〴δΗÄδΗΣδΨ΄ε≠?5,7,9)εQ¨εΤàε¹΅η°ΨδΜé㧧δΗÄε†Üεè•δΜάL³èKεΦ†γâ¨ψÄ?/p>
φé£ιôΛΫW§δΗÄε†Üγâ¨γö³nim-sumδΗ?7^9=14
0111
^1001
-------
1110
εΠ²φû€ηΠ¹δ΄…φâÄφ€âε†Üγö³nim-sum=0φàêγΪ΄εQ¨εàôΫW§δΗÄε†Üεè•φéâKεΦ†δΜΞεêéεΩÖε°öδΊ™1110εQ¨ε¦†δΗΚX^X=0ψÄ?/p>
φâÄδΜΞηΠ¹ηß²ε·ü 5-k=14 k>0 φàêγΪ΄,φ≠ΛδΨ΄ε≠?倮㧧δΗÄε†Üεè•δΜάL³èKεΦ†γâ¨)φ‰éφ‰Ψγö³δΗçφàêγΪ΄ψIJδΫÜρqΕδΗçδΜΘηî倮㧧δΚ¨φà•ΫW§δΗâε†Üεè•δΜάL³èKεΦ†γâ¨γö³ηßΘδΗçφàêγΪ΄ψÄ?/p>
2. γéΑ倮〴㧧δΚ¨δΗΣδΨ΄ε≠ê(15,7,9)εQ¨εΤàε¹΅η°ΨδΜé㧧δΗÄε†Üεè•δΜάL³èKεΦ†γâ¨ψÄ?/p>
φé£ι‰üΫW§δΗÄε†Üγâ¨γö³nim-sumδΗ?^9=14εQ¨ε£¨ΫW§δΗÄδΗΣδΨ΄ε≠êγ¦Ηεê¨οΦ¨φâÄδΜΞι½°ιΔ‰εè‰δΗχôß²ε·?15-k=14 k>0 φ‰·εêΠφàêγΪ΄ψÄ?/p>
εΫ™γ³Ε‰qôδΗΣδΨ΄ε≠êφ‰·φàêγΪ΄γö³ψÄ?/p>
δΗ?
φÄ»ùΜ™εΨ½ε΅ΚεQ?/p>
ε€®δ™Qφ³èδΗÄε†Üφ΄ΩδΜάL³èKεΦ†γâ¨εQ¨εΤàδΗîφâÄφ€âε†Üγö³nim-sum=0 φàêγΪ΄γö³φùΓδΜΕδΊ™εQöφé£ιôΛεè•φéâKεΦ†γâ¨γö³ι²ΘδΗÄε†Üγö³nim-sumεΩÖιΓΜû°ëδΚéη·Ξε†Üγâ¨δΗäγö³φïΑι΅?δΨ΄ε≠êδΚ?εQ¨εêΠεàôδΗçηÉΫε€®φ≠Λε†ÜδΗäεè•δΜάL³èKεΦ†γâ¨δΫΩφâÄφ€âε†Üγö³nim-sum=0φàêγΪ΄(δΨ΄ε≠êδΗÄ)ψÄ?/p>
φïÖφÄάL•ΙφΓàφïΑδΗ?( ε€®δ™Qφ³èδΗÄε†Üφ΄ΩδΜάL³èKεΦ†γâ¨εQ¨εΤàδΗîφâÄφ€âε†Üγö³nim-sum=0 φàêγΪ΄ ) γö³φÄάLïΑψÄ?/p>
δΜΘγ†¹εΠ²δΗ΄ :
#include <iostream>
int heap[101];
int main ()
{
int T;
while ( scanf ( "%d",&T ), T )
{
int res = 0 , nCount = 0;
for ( int i = 0; i != T; ++ i )
{
scanf ( "%d",heap + i );
res ^= heap[i];
}
if ( res == 0 )
{
puts ( "0" );
continue;
}
int cmp = 0;
for ( int i = 0; i != T; ++ i )
{
cmp = res ^ heap[i];
if ( cmp < heap[i] )
{
nCount ++;
}
}
printf ( "%d\n",nCount );
}
return 0;
}
ιΔ‰γ¦°ε€ΑεùÄ:
http://acm.hdu.edu.cn/showproblem.php?pid=2897
ιΔ‰γ¦°φèèηΩΑ:
εΫ™φ½Ξι¹΅εàΑφ€àοΦ¨δΚéφ‰·φ€âδΚÜφ‰éψIJεΫ™φàëι¹΅εàνCΚÜδΫ†οΦ¨δΨΩφàêδΚÜδ«GψÄ?br>ι²ΘεΛ©εQ¨φ½Ξφ€àγ¦ΗδΦöοΦ¨φàëηß¹εàνCΚÜδΫ†ψIJηĨδΗîεQ¨εΛßε€ΑεΛ±εé÷MΚÜεÖâηΨâεQ¨δΫ†φàëφ‰·εêΠφàêδΨΘοΦü‰qôφ≥®ε°öφ‰·δΗΣε΅³Ψüéγö³φïÖδΚ΄ψIJοΦàδΜΞδΗäφ‰·εΚüη·ùοΦâ
û°èt壨φâÄφ€âδΗ•δΩ½γö³δΚόZΜ§δΗÄφ†χPΦ¨φ€üεΨÖι²ΘγôΨρq¥ιöΨι¹΅γö³φ½ΞιΘüψIJι©Μ≠ë¨ôΓ½ε˥〴εΛ©ο֨〴φ½Ξφ€àφΗêφΗêηΒΑ‰qëοΦ¨û°ètγö³η³•ε≠êι²ΘδΗΣιÖΗεëÄεQàδΜ•εùöφ¨¹‰qôδΗΣεßΩεäΩεΖ≤γΜèφ€âεçäδΗΣεΛöû°èφ½ΕεïΠοΦâψIJδΜ•δΫéδΗ΄δΜΑη™vγö³εΛ¥εQ¨γé·ôεë÷¦¦εë®ψIJεΩΫγ³ΕεèëγéΑημnηΨΙγΪüγΪôγùÄδΫçφΦ²δΚ°γö³mmψIJεΛ©φΗêφΗêφö½δΗ΄εQ¨ηΩômmε€®ηΩôηΓ½εΛ¥γΪüγ³ΕεΠ²φ≠ΛηÄÄγ€ϊ|Φ¨εΞ“é‰·εΛ©δ΄…εê½οΦüγΪôγùÄû°ètμwΪηΨΙγö³εΛ©δΫ―ùÄ?br>û°ètε·ΙmmφÉäεëΦεQ?#8220;Ψ~‰εàÜεë?/span>~~”ψIJmmεç¥φ·ΪδΗçεêΪΨpäοΦö“φ‰·εïäεQ?00ρq¥δΗÄι¹΅ε™ΠεQ?#8221;εQàφ≠Λεêéγ€¹γï?000ε≠?#8230;.εQ?br>û°ètηΒΕγ¥ßεêëmmηΠ¹η¹îΨpάL•ΙεΦèοΦ¨εè·mmη·Ώ_Φö“φàë壨δΫ†γé©δΗΣφΗΗφàèεêßεQ¨ηΒΔδΚÜοΦ¨φàëεΑ±φääφàëγö³φâ΄φ€ΚεèΖεëäη·âδΫ†ψÄ?#8221;û°ètεQ¨εΩÉφɦ_Λ©δΗ΄ε™Σφ€âιΔ‰γ¦°ηÉΫιöë÷Ä£φàëεëΔοΦ¨δΨΩφΜΓεèΘγ≠îεΚîδΗ΄φùΞψIJmmεΦÄεß΄η·¥φΗΗφàèηß³εàôεQ?#8220;φàëφ€âδΗÄε†ÜγΓ§εΗ¹οΦ¨δΗÄεÖ?φûöοΦ¨δΜéηΩôδΗΣγΓ§εΗ¹ε†Ü顨εè•Φ΄§εΗ¹εQ¨δΗÄ΄ΤΓφ€Äû°ëεè•2φûöοΦ¨φ€ÄεΛ?φûöοΦ¨εΠ²φû€εâ©δΗ΄û°ëδΚé2φûöεΑ±ηΠ¹δΗÄ΄ΤΓεè•ε°¨ψIJφàë壨δΫ†ηΫ°φΒ¹εè•ο֨㦥εàΑε†Ü顨γö³γΓ§εΗ¹εè•ε°¨οΦ¨φ€ÄεêéδΗÄ΄ΤΓεè•Φ΄§εΗ¹γö³γ°½ηΨ™ψIJφàëγé©ηΩ΅‰qôδΗΣφΗΗφàèεΞΫεΛö΄ΤΓδΚÜεQ¨εΑ±η°©η°©δΫ†οΦ¨η°©δΫ†εÖàεè•εê?/span>~”
û°ètφéêφ¨΅δΗÄΫé½οΦ¨δΗçε·ΙεëÄεQ¨ηΩôφ‰·δΗçεè·ηÉΫγö³δ™QεäΓδΙàψIJεΑètι€≤ε΅ΚεΨ½φ³èγö³γ§ëεQ?#8220;‰q‰φ‰·mmδΦ‰εÖàεïΠοΦ¨εëΒεëΒ~”mmι€éφ½Εφ³ΘδΫèδΚÜοΦ¨φÉœx‰·ε·ΙεΑètγö³εèçεΚîε΅ΚδΙéφ³èφ•ôεêßψÄ?br>εΞΙεç¥δΙüδΗçγîüφΑîεQ?#8220;εΞΫεΑèε≠êοΦ¨φ¨χô¹Σφ‰éεëΔεQ¨ηΠ¹δΗçηΩôφ†ΖεêßεQ¨δΫ†φääφàëγö³ι²°ΫéόqΜôφàëοΦ¨φàëγΜôδΫ†εèëδΗΣφ•΅φ€§οΦ¨φ·èηΓ¨φ€âδΗâδΗΣφïΑε≠½nεQ¨pεQ¨qεQ¨ηΓ®ΫCόZΗÄε†ÜγΓ§εΗ¹δΗÄεÖ±φ€ânφûöοΦ¨δΜéηΩôδΗΣγΓ§εΗ¹ε†Ü顨εè•Φ΄§εΗ¹εQ¨δΗÄ΄ΤΓφ€Äû°ëεè•pφûöοΦ¨φ€ÄεΛöqφûöοΦ¨εΠ²φû€εâ©δΗ΄û°ëδΚépφûöεΑ±ηΠ¹δΗÄ΄ΤΓεè•ε°¨ψIJδΗΛδΚχôΫ°΄Ι¹εè•εQ¨γ¦¥εàΑε†Ü顨γö³Φ΄§εΗ¹εè•ε°¨εQ¨φ€ÄεêéδΗÄ΄ΤΓεè•Φ΄§εΗ¹γö³γ°½ηΨ™ψIJε·ΙδΚéφ·èδΗÄηΓ¨γö³δΗâδΗΣφïΑε≠½εQ¨γΜôε΅ΚεÖàεè•γö³δΚΚφ‰·εêΠφ€âεΩÖηÉ€Ϋ{•γïΞεQ¨εΠ²φû€φ€âε¦ûγ≠îWINεQ¨εêΠεàôε¦ûΫ{îLOSTψIJδΫ†φääε·ΙεΚîγö³Ϋ{îφΓàεèëγΜôφàëοΦ¨εΠ²φû€δΫ†ηÉΫε€®δΜäεΛ©φôöδΗ?γ²ΙδΜΞεâçεèëΨlôφàëφ≠ΘγΓ°Ϋ{îφΓàεQ¨φà•η°ΗφàëδΜ§φ‰éεΛ©δΗ΄εçàεè·δΜΞεÜçηß¹ψÄ?#8221;
û°ètδΚ¨η·ùφ≤Γη·¥εQ¨εΑÜη΅ΣεΖ±γö³ι²°ΫéόqΜôδΚÜmmψIJεΫ™δΜ•εÖ¥εÜ≤εÜ≤εΨ½ηΒΕε¦ûε°ΕεQ¨δΗäΨ|ë〴鲰㰱εQ¨ε™΅εQ¹mmγö³ι²°δΜΕεΖ≤ΨlèεàΑδΚÜψIJδΜ•εèëγéΑφ•΅φ€§ιïΩηΨΨ100000ηΓ¨οΦ¨φ·èηΓ¨γö³δΗâδΗΣφïΑε≠½ιÉΫεΨàεΛßεQ¨δΫÜφ‰·ιÉΫφ‰·δΗç≠ëÖηΩ΅65536γö³φï¥φïΑψIJεΑèt〴ηΓ®εΖ≤γΜèδΗ΄εçà6γ²ΙδΚÜεQ¨ηΠ¹φÉœxâ΄εΖΞγ°½ε΅ΚφâÄφ€âγΜ™φû€ο֨〴φùΞφ‰·δΗçεè·ηÉΫδΚÜψIJδΫ†ηÉΫεΗ°εΗ°δΜ•εQ¨η°©δΜ•εÜçηß¹εàΑι²ΘδΗΣmmεê½οΦü
Input
δΗçηΕÖ‰q?00000ηΓ¨οΦ¨φ·èηΓ¨δΗâδΗΣφ≠Θφï¥φïΑnεQ¨pεQ¨qψÄ?br>
Output
ε·ΙεΚîφ·èηΓ¨ηΨ™εÖΞεQ¨φ¨âεâçιùΔδΜ΄γΜçγö³φΗΗφàèηß³εàôοΦ¨εàΛφ•≠εÖàεè•ηÄÖφ‰·εêΠφ€âεΩÖηÉ€Ϋ{•γïΞψIJηΨ™ε΅ΚWINφà•ηÄÖLOSTψÄ?br>
Sample Input
7 2 4
6 2 4
Sample Output
LOST
WIN
εçöεΦàγö³εÖΞι½®ιΔ‰, εΖ¥δΜÄεçöεΞï(Bash Game), εÖΖδΫ™δΚÜηßΘη·οL²Ιε΅?nbsp; εçöεΦàεÖΞι½® .
δΜΘγ†¹εΠ²δΗ΄:
#include <iostream>
int main ()
{
int N, p, q;
while ( scanf ( "%d%d%d",&N, &p, &q ) != EOF )
{
int res = N % ( p + q );
puts ( res ? res <= p ? "LOST" : "WIN" : "WIN" );
}
return 0;
}
εèΠεΛ•ΩUÄΩUÄη΅ΣεΖ±γö³δΗÄηΓ¨δΜΘγ†?:
main(p,q){int N,res;while(~scanf("%d%d%d",&N,&p,&q)){res=N%(p+q);puts(res?res<=p?"LOST":"WIN":"WIN");}}
ε·άLâΨρq¨ôΓΓγäΕφĹοΦàδΙüγßΑεΩÖη”|φĹοΦ¨ εΞ΅εΦ²ε±ÄεäΩοΦâεQ¨οΦàφΜΓηÉωεQöδ™Qφ³èιùûρq¨ôΓΓφĹγΜè‰q΅δΗÄ΄ΤΓφ™çδΫ€εè·δΜΞεè‰δΗΚεψ^ηΓΓφĹοΦâ
(δΗÄ)εΖ¥δΜÄεçöεΞï(Bash Game):
εèΣφ€âδΗÄε†?/span>nδΗΣγâ©ε™?/span>,δΗΛδΗΣδΚχôΫ°΄Ι¹δΜé‰qôε†Üγâ©ε™¹δΗ≠εè•γâ?/span>,ηß³ε°öφ·èφ§Γ硦_Αëεè•δΗÄδΗ?/span>,φ€ÄεΛöεè•mδΗ?/span>.φ€Äεêéεè•εÖâηÄÖεΨ½ηÉ?/span>.
n = (m+1)r+s , (rδΗόZ™Qφ³èη΅Σγ³ΕφïΑ,s≤m), εç?/span>n%(m+1) != 0, εàôεÖàεè•ηÄÖη²·ε°öηéΖηÉ?/span>
(δΚ?/span>)ε®¹δΫêεΛΪεçöεΞ?/span>(Wythoff Game):
φ€âδΗΛε†Üεê³η΄ΞεΙ≤δΗΣγâ©ε™?/font>,δΗΛδΗΣδΚχôΫ°΄Ι¹δΜéφüêδΗÄε†Üφà•εê¨φ½ΕδΜéδΗΛε†ÜδΗ≠εè•εê¨φ†ΖεΛöγö³γâ©ε™?/font>,ηß³ε°öφ·èφ§Γ硦_Αëεè•δΗÄδΗ?/font>,εΛöηÄÖδΗçιô?/font>,φ€Äεêéεè•εÖâηÄÖεΨ½ηÉ?/font>.
(ak,bk)(ak ≤ bk ,k=0,1,2,...,n)ηΓ®γΛΚεΞ΅εΦ²ε±Äεä?/span>
φ±²φ≥ïεQ?/span>
ak =[k(1+√5)/2], bk= ak + k (k=0,1,2,...,n φ•“é΄§εè·²Γ®ΫCΚεè•φï¥ε΅Ϋφï?/span>)
εàΛφ•≠εQ?/span>
Gold=(1+sqrt(5.0))/2.0εQ?/span>
1εQâε¹΅η°ΨοΦàaεQ?/span>bεQâδΊ™ΫW?/span>kΩUçεΞ΅εΦ²ε±Äεä?/span>(k=0,1,2...) ι²ΘδΙàk=b-a;
2εQâεàΛφ•≠εÖΕa==(int)(k*Gold),γ¦Ηγ≠âεàôδΊ™εΞ΅εΦ²ε±Äεä?/span>
εQàφ≥®εQöι΅΅γî®ιIJεΫ™γö³φ•Ιφ≥?/span>,εè·δΜΞû°ÜιùûεΞ΅εΦ²ε±ÄεäΩεè‰δΗΚεΞ΅εΦ²ε±Äεä?/span>.
ε¹΅η°ΨιùΔε·Ιγö³ε±ÄεäΩφ‰·(a,b)
η΄?/span> b = a,εàôεê¨φ½ΕδΜéδΗΛε†ÜδΗ≠εè•ηΒ?/span> a δΗΣγâ©δΫ?/span>,û°±εè‰δΗόZΚÜεΞ΅εΦ²ε±Äεä?/span>(0,0)εQ?/span>
1. εΠ²φû€a = ak,
1.1 b > bk, ι²ΘδΙà,εè•ηΒΑb - bkδΗΣγâ©δΫ?/span>,εç¦_è‰δΗΚεΞ΅εΦ²ε±Äεä?/span>(ak, bk)εQ?/span>
1.2 b < bk εàôεê¨φ½ΕδΜéδΗΛε†ÜδΗ≠φ΄ΩηΒ?/span> ak – a[b – ak]δΗΣγâ©δΫ?/span>,εè‰δΊ™εΞ΅εΦ²ε±Äεä?/span>( a[b – ak] , a[b – ak]+ b - ak)εQ?/span>
2 εΠ²φû€a = bk ,
2.1 b > ak ,εàôδΜéΫW§δΚ¨ε†ÜδΗ≠φ΄ΩηΒΑεΛöδΫôγö³φïΑι΅?/span>b – ak
2.2 b < ak ,εà?/span> η΄?/span>b = aj (j < k) δΜé㧧δΗÄε†ÜδΗ≠φ΄ΩηΒΑεΛöδΫôγö³φïΑι΅?/span>a– bj; (a > bj)
η΄?/span>b = bj (j < k) δΜé㧧δΗÄε†ÜδΗ≠φ΄ΩηΒΑεΛöδΫôγö³φïΑι΅?/span>a– aj; ( a > aj)
εQ?/span>
δΨ΄ιΔ‰εQ?/span>pku 1067
(δΗ?/span>)û°ΦεßÜεçöεΞï(Nimm Game):
φ€?/font>nε†Üεê³η΄ΞεΙ≤δΗΣγâ©ε™?/font>,δΗΛδΗΣδΚχôΫ°΄Ι¹δΜéφüêδΗÄε†Üεè•δΜάL³èεΛöγö³γâ©ε™¹,ηß³ε°öφ·èφ§Γ硦_Αëεè•δΗÄδΗ?/font>,εΛöηÄÖδΗçιô?/font>,φ€Äεêéεè•εÖâηÄÖεΨ½ηÉ?/font>.
δΜ÷MΫïεΞ΅εΦ²ε±Äεä?/span>(a1, a2, … , an)ιÉΫφ€âa1(+)a2(+)…(+)an =0. ( (+)δΗ?/span> φ¨âδΫç^)
NimφΗΗφàèΫéÄδΜ΄οΦö
εQ?εQâφ€âδΗΛδΗΣγé©ε°ΕεQ?/p>
εQ?εQâφ€âδΗâε†ÜφâëεÖ΄γâ¨οΦàφ·îεΠ²εQöεè·δΜΞεàÜεàΪφ‰·5εQ?εQ?εΦ†οΦâεQ?/p>
εQ?εQâγé©ε°Εγö³φ·èφ§Γφ™çδΫ€φ‰·ιÄâφ΄©εÖΕδΗ≠φüêδΗÄε†Üγâ¨εQ¨γ³ΕεêéδΜéδΗ≠εè•ηΒνC™Qφ³èεΦ†εQ?/p>
nimφΗΗφàèγö³ε°öγêÜδΗÄεQ?/p>
ε·ΙδΚénimφΗΗφàèγö³φüêδΗΣδΫçΨ|?x1,x2,x3),εΫ™δΗîδΜÖεΫ™ε°Éεê³ιÉ®εàÜγö³nim-sumΫ{âδΚé0φ½”ûΦàεç≥x1⊕x2⊕x3=0εQâοΦàx1εQ¨x2εQ¨x3ε¹öεΦ²φà•φ™çδΫ€^εQâοΦ¨εàôεΫ™εâçδΫçδΚéεΩÖη¥Ξγ²ΙψÄ?/p>
δΨ΄ιΔ‰εQ?/span>pku 2234 δΨ΄ιΔ‰εQ?/span>hdu 1730 δΨ΄ιΔ‰εQ?/span>pku 1740 δΨ΄ιΔ‰εQ?/span>pku 1704 δΨ΄ιΔ‰εQ?/span>pku 1082 (εΛßι΅èεàÜφûê… Ψl™η°ΚεΨàγ°ÄεçïψÄ?/span> δΙüεè·δΜΞφ†Ιφç°γ°Äεçïγö³φé®η°Κφ®Γφ΄üε°ûγéΑψÄ?/span>)
ε°öδΙâ: ε¹΅η°Ψ (xm · · · x0)2 ε£?ym · · · y0)2 γö³nim-sumφ‰?zm · · · z0)2,εàôφàëδΜ§ηΓ®ΫCΚφàê (xm · · · x0)2 ⊕ (ym · · · y0)2 = (zm · · · z0)2,
‰qô顨εQ¨zk = xk + yk (mod 2)εQàk=0…mεQ? 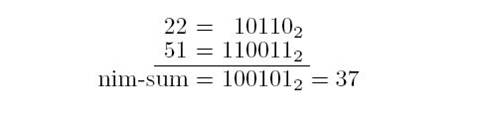
ιΔ‰γ¦°ε€ΑεùÄ :
http://acm.hdu.edu.cn/showproblem.php?pid=1133
ιΔ‰γ¦°φèèηΩΑ:
The "Harry Potter and the Goblet of Fire" will be on show in the next few days. As a crazy fan of Harry Potter, you will go to the cinema and have the first sight, won’t you?
Suppose the cinema only has one ticket-office and the price for per-ticket is 50 dollars. The queue for buying the tickets is consisted of m + n persons (m persons each only has the 50-dollar bill and n persons each only has the 100-dollar bill).
Now the problem for you is to calculate the number of different ways of the queue that the buying process won't be stopped from the first person till the last person.
Note: initially the ticket-office has no money.
The buying process will be stopped on the occasion that the ticket-office has no 50-dollar bill but the first person of the queue only has the 100-dollar bill.
Input
The input file contains several test cases. Each test case is made up of two integer numbers: m and n. It is terminated by m = n = 0. Otherwise, m, n <=100.
Output
For each test case, first print the test number (counting from 1) in one line, then output the number of different ways in another line.
Sample Input
3 0
3 1
3 3
0 0
Sample Output
Test #1:
6
Test #2:
18
Test #3:
180
εçΓγâΙεÖΑφïΑγö³εΚîγî®~~~ ^_^
1133 εÖ§εΦèφé®ε·ΦεΠ²δΗ΄ :
( C(m+n, n) - C(m+n, m+1) ) * m! * n! 娕γ°Äεç?nbsp;(m+n)! * (m-n+1) / (m+1)
φé®ε·Φ‰q΅γ®΄εΠ²δΗ΄ :
mδΗΣδùhφ΄?0εQ¨nδΗΣδùhφ΄?00
1: φâÄδΜΞεΠ²φû?nbsp;n > mεQ¨ι²ΘδΙàφé£εΚèφ•Ιφ≥ïφïΑδΗ?nbsp;0 ‰qôδΗÄγ²ΙεΨàε°“é‰™φÉœxΗÖφΞ?nbsp;
2: γéΑε€®φàëδΜ§ε¹΅η°Ψ φ΄?0γö³δùhγî?nbsp;‘0’ηΓ®γΛΚεQ?nbsp;φ΄?00γö³δùhγî?nbsp;1 ηΓ®γΛΚψÄ?br>
εΠ²φû€φ€âηΩôδΙàδΗÄδΗΣεΚèεà?nbsp;0101101001001111.
εۙ㧧KδΗΣδΫçΨ|°ε΅Κγé?γö³δΗΣφïΑεΛöδΫ?γö³δΗΣφïΑφ½Εû°±φ‰·δΗÄδΗΣδΗçεêàφ≥ïεΚèεà½δΚ?br>
ε¹΅η°Ψm=4 n=3γö³δΗÄδΗΣεΚèεà½φ‰·εQ?/span>0110100 φ‰³Γ³ΕεQ¨ε°ÉδΗçεêàφ≥ïοΦ¨ γéΑε€®φàëδΜ§φääε°ÉΫEçεΨ°εè‰ε¨•δΗÄδΗ΄οΦö
φää㧧δΚ¨δΗΣ1εQàηΩôδΗ?εâçιùΔγö³ιÉΫφ‰·εêàφ≥ïγö³εQâεêéιùΔγö³φâÄφ€âδΫç0εè‰φàê1εQ?εè‰φàê0
û°±εΨ½εà?nbsp;0111011 ‰qôδΗΣεΚèεà½1γö³φïΑι΅èεΛöδΚ?γö³φïΑι΅èοΦ¨ φ‰³Γ³ΕδΗçεêàφ≥ïοΦ¨ δΫÜγéΑε€®γö³εÖ≥ιî°δΗçφ‰·γ€΄ηΩôδΗΣεΚèεà½φ‰·δΗçφ‰·εêàφ≥ïγö?nbsp;
εÖ≥ιî°φ‰·οΦöε°É壨φàëδΜ§γö³δΗçεêàφ≥ïεΚèεའ0110100 φàêδΗÄδΗÄε·ΙεΚîγö³εÖ≥Ψp?nbsp;
δΙüεΑ±φ‰·η·¥δΜάL³èδΗÄδΗΣδΗçεêàφ≥ïεΚèεà½(mδΗ?εQ¨nδΗ?)εQ?nbsp;ιÉΫεè·δΜΞγî±εèΠεΛ•δΗÄδΗΣεΚèεà?n-1δΗ?壨m+1δΗ?)εΨ½εàΑ
εèΠεΛ•φàëδΜ§γüΞι¹™εQ¨δΗÄδΗΣεΚèεà½ηΠ¹δΙàφ‰·εêàφ≥ïγö³οΦ¨ηΠ¹δΙàφ‰·δΗçεêàφ≥ïγö?nbsp;
φâÄδΜΞοΦ¨εêàφ≥ïεΚèεà½φïΑι΅è = εΚèεà½φÄάLïΑι΅?nbsp;- δΗçεêàφ≥ïεΚèεà½γö³φÄΜι΅è
εΚèεà½φÄάLïΑεè·δΜΞ‰qôφ†Ζη°Γγ°½m+n δΗΣδΫçΨ|°δΗ≠εQ?nbsp;ιÄâφ΄© n δΗΣδΫçΨ|°ε΅ΚφùΞεΓΪδΗ?nbsp;1εQ?nbsp;φâÄδΜΞφ‰· C(m+n, n)
δΗçεêàφ≥ïεΚèεà½γö³φïΑι΅èû°±φ‰·εQ?nbsp;m+n δΗΣδΫçΨ|°δΗ≠εQ?nbsp;ιÄâφ΄© m+1 δΗΣδΫçΨ|°ε΅ΚφùΞεΓΪδΗ?nbsp;1 φâÄδΜΞφ‰· C(m+n, m+1)
γ³Εεêéφ·èδΗΣδΚΚιÉΫφ‰·δΗçδΗÄφ†οLö³εQ¨φâÄδΜΞι€ÄηΠ¹εÖ®φé£εའm! * n!
φâÄδΜΞφ€Äεêéγö³εÖ§εΦèδΗ?: ( C(m+n, n) - C(m+n, m+1) ) * m! * n! 娕γ°Äεç?nbsp;(m+n)! * (m-n+1) / (m+1)
φé®εΙΩ:
εΠ²φû€εéüφùΞφ€âpεΦ?0εÖÉγö³η·?ι²ΘδΙàδΗçεêàφ≥ïγö³εΚèεà½γö³φïΑι΅èεΚîη·Ξφ‰·:δΜάL³èδΗÄδΗΣδΗçεêàφ≥ïεΚèεà½(mδΗ?εQ¨nδΗ?)εQ?br>
ιÉΫεè·δΜΞγî±εèΠεΛ•δΗÄδΗΣεΚèεà?n-1δΗ?壨m+1+pδΗ?)εΨ½εàΑ,φâÄδΜΞφ‰·m+n δΗΣδΫçΨ|°δΗ≠εQ?nbsp;ιÄâφ΄© m+1+p δΗΣδΫçΨ|?br>
ε΅ΚφùΞεΓΪδΗä 1 φâÄδΜΞφ‰· C(m+n, m+1+p) φéΞδΗ΄φùΞγö³ε¨•γ°Äû°ΉÉΗçφé®δΚÜ.
δΜΘγ†¹εΠ²δΗ΄ :
#include <iostream>
#include <string>
using namespace std;
#define MAX 100
#define BASE 10000
void multiply(int a[],int Max,int b) //εΛßφïΑδΙ‰εΑèφï?/span>
{
int i,array=0;
for (i=Max-1; i>=0; i--)
{
array+=b*a[i];
a[i] = array%BASE;
array /= BASE;
}
}
void divide(int a[], int Max, int b) //εΛßφïΑιôΛεΑèφï?/span>
{
int i,div=0;
for (i=0;i<Max; i++)
{
div = div*BASE + a[i];
a[i] = div / b;
div %= b;
}
}
int fact[205][MAX];
void setFact ()
{
fact[0][MAX-1] = fact[1][MAX-1] = 1;
for ( int i = 2; i <= 200; ++ i )
{
memcpy ( fact[i] , fact[i-1] , MAX * sizeof ( int ) );
multiply ( fact[i] , MAX , i );
}
}
void outPut ( int ctl[MAX] )
{
int i = 0;
while ( i < MAX && ctl[i] == 0 )
{
i ++ ; //εé’dâçε·?
}
printf ( "%d", ctl[i++] );
while ( i < MAX )
{
printf ( "%04d", ctl[i++] );
}
putchar ( '\n' );
}
int res[MAX];
int main ()
{
int M,N;
int ca = 1;
setFact();
while ( cin >> M >> N , M + N )
{
printf ( "Test #%d:\n",ca++ );
if ( N > M )
{
puts ( "0" );
continue;
}
memcpy ( res , fact[M+N] , MAX * sizeof ( int ) ); ι‰ΕδΙ‰ ( m + n )!
multiply ( res, MAX, M - N + 1 ); ( m + n )! * ( m-n+1 )
divide ( res, MAX, M + 1 ); ( m + n )! * ( m-n+1 ) / ( m+ 1 )
outPut ( res );
}
return 0;
}
φ¦¥εΛöεçΓγâΙεÖΑφïΑηΒ³φ•ô η·οL€΄ εçΓγâΙεÖΑφïΑ
HDU 1023 1130 1134 2067 ιÉΫφ‰·φ†΅ε΅Üγö³εçΓγâΙεÖΑφï? εÖΖδΫ™η·¥φ‰éη··²ß¹ εçΓγâΙεÖΑφïΑ ,εèΣφ‰·φ€âδΗÄγ²öw€ÄηΠ¹φ≥®φ³? ε€?5δΜ?/span>δΗ΄γö³catalanφï?br>
εè·δΜΞ㦥φéΞδΫΩγî® long long φà?__int64 φèêδΚΛγö? δΫÜφ‰·εΫ?N ≠ëÖηΩ΅35 δΙ΄εêé, ‰qôεΑ±ι€ÄηΠ?span style="COLOR: red">εΛßφïΑδΚ?
δΗ΄ιùΔφ‰?2067 γö?long long δΜΘγ†¹ ,η·ΠγΜÜη··²ß¹ ( 2067 û°èεÖîγö³φΘ΄γ¦?ηßΘιΔ‰φäΞεëä ) φ≤Γφ€âδΫΩγî®ιÄ£εΫ£εΦ?, 㦥φéΞγî®γö³catalan γö?‰q≠δΜΘεΦ? :
#include<iostream>
using namespace std;
typedef long long int64;
int64 f[37][37];
int main()
{
int ca=0;
int N;
while ( cin >> N , N + 1 )
{
++ ca;
for ( int i = 1;i <= N; ++ i )
{
f[0][i] = 1;
}
for ( int i = 1; i < N; ++ i )
{
for ( int j = i; j <= N; ++ j )
{
if ( i == j )
{
f[i][j] = f[i-1][j];
}
else
{
f[i][j] = f[i-1][j] + f[i][j-1];
}
}
}
printf("%d %d %I64d\n", ca, N, 2 * f[N-1][N] );
}
return 0;
}
ιôΛδΚÜ 2067 εΛ? εÖΕδΜ•γö³ιΔ‰γ¦°εù΅φ‰·εΛßφïΑγö³Ψc’dû΄, ε€®ηΩôι΅? εê³δΫç ACMer , η·Ζε΅ΚδΫ†δΜ§γö³εΛßφïΑφ®ΓφùΩεêß .
φà•ηÄÖφüêδΚ¦δΜΘγ†¹γâ¦δΚΚεè·δΜΞη΅ΣεΖ±φâ΄φâ?nbsp;<-------0rz
εÜôεΞΫδΜΘγ†¹εê?εèΣι€Äφ¨âιΔ‰γ¦°ηΠ¹φ±²φ†ΦεΦèε¹öγ¦ΗεΚîγö³φîΙεè? δΨΩηÉΫ㦥φéΞAC. 1133 ΫEçεΨ°φ€âγ²ΙδΗçεê¨. δΦöε€®
φ€ÄεêéγΜôε΅Κε°Éγö³ηßΘιΔ‰φäΞεë?
1023 1130 1134 㦥φéΞδΫΩγî® catalanφï?γö³ιÄ£εΫ£εΦ?,δΜΘγ†¹εΠ²δΗ΄, δΫΩγî®γö³φ‰·ιΪ‰γ≤ΨεΚΠδΙ‰φ≥? ( ι€ÄηΠ¹ε€®ηΨ™εÖΞΨl™φùüφéßεàΕφ•öwùΔφ†“éç°εê³ιΔ‰ε¹öγ¦ΗεΚîεè‰ε¨?) :
#include<iostream>
using namespace std;
#define MAX 105
#define BASE 10000
typedef int myType[MAX+10];
void multiply ( int a[], int Max, int b ) //εΛßφïΑδΙ‰εΑèφï?/span>
{
int i,array=0;
for (i=Max-1; i>=0; i--)
{
array+=b*a[i];
a[i] = array%BASE;
array /= BASE;
}
}
void divide ( int a[], int Max, int b ) //εΛßφïΑιôΛεΑèφï?/span>
{
int i,div=0;
for (i=0;i<Max; i++)
{
div = div*BASE + a[i];
a[i] = div / b;
div %= b;
}
}
void outPut ( myType ctl[MAX] ,int N )
{
int i = 0;
while ( i < MAX && ctl[N][i] == 0 )
{
i ++ ; //εé’dâçε·?
}
cout << ctl[N][i++];
while ( i < MAX )
{
printf ( "%04d", ctl[N][i++] );
}
cout << endl;
}
void setNum ( myType ctl[MAX] )
{
memset ( ctl[1], 0, MAX * sizeof ( int ) );
ctl[1][MAX-1] = 1;
for ( int i = 2; i < 101; i ++ )
{
memcpy ( ctl[i], ctl[i-1], MAX * sizeof ( int ) );
multiply ( ctl[i], MAX, 4 * i - 2 );
divide ( ctl[i], MAX, i + 1 );
}
}
myType ctl[MAX];
int main()
{
setNum ( ctl );
int N;
while ( cin >> N ) // ‰qô顨φ†“éç°εê³ιΔ‰ηΠ¹φ±²ι€ÄηΠ¹ε¹öγ¦ΗεΚîεè‰ε¨•
{
outPut ( ctl, N );
}
return 0;
}
1133 εÖ§εΦèφé®ε·ΦεΠ²δΗ΄ :
( C(m+n, n) - C(m+n, m+1) ) * m! * n! 娕γ°Äεç?nbsp;(m+n)! * (m-n+1) / (m+1)
φé®ε·Φ‰q΅γ®΄εΠ²δΗ΄ :
mδΗΣδùhφ΄?0εQ¨nδΗΣδùhφ΄?00
1: φâÄδΜΞεΠ²φû?nbsp;n > mεQ¨ι²ΘδΙàφé£εΚèφ•Ιφ≥ïφïΑδΗ?nbsp;0 ‰qôδΗÄγ²ΙεΨàε°“é‰™φÉœxΗÖφΞ?nbsp;
2: γéΑε€®φàëδΜ§ε¹΅η°Ψ φ΄?0γö³δùhγî?nbsp;‘0’ηΓ®γΛΚεQ?nbsp;φ΄?00γö³δùhγî?nbsp;1 ηΓ®γΛΚψÄ?br>
εΠ²φû€φ€âηΩôδΙàδΗÄδΗΣεΚèεà?nbsp;0101101001001111.
εۙ㧧KδΗΣδΫçΨ|°ε΅Κγé?γö³δΗΣφïΑεΛöδΫ?γö³δΗΣφïΑφ½Εû°±φ‰·δΗÄδΗΣδΗçεêàφ≥ïεΚèεà½δΚ?br>
ε¹΅η°Ψm=4 n=3γö³δΗÄδΗΣεΚèεà½φ‰·εQ?/span>0110100 φ‰³Γ³ΕεQ¨ε°ÉδΗçεêàφ≥ïοΦ¨ γéΑε€®φàëδΜ§φääε°ÉΫEçεΨ°εè‰ε¨•δΗÄδΗ΄οΦö
φää㧧δΚ¨δΗΣ1εQàηΩôδΗ?εâçιùΔγö³ιÉΫφ‰·εêàφ≥ïγö³εQâεêéιùΔγö³φâÄφ€âδΫç0εè‰φàê1εQ?εè‰φàê0
û°±εΨ½εà?nbsp;0111011 ‰qôδΗΣεΚèεà½1γö³φïΑι΅èεΛöδΚ?γö³φïΑι΅èοΦ¨ φ‰³Γ³ΕδΗçεêàφ≥ïοΦ¨ δΫÜγéΑε€®γö³εÖ≥ιî°δΗçφ‰·γ€΄ηΩôδΗΣεΚèεà½φ‰·δΗçφ‰·εêàφ≥ïγö?nbsp;
εÖ≥ιî°φ‰·οΦöε°É壨φàëδΜ§γö³δΗçεêàφ≥ïεΚèεའ0110100 φàêδΗÄδΗÄε·ΙεΚîγö³εÖ≥Ψp?nbsp;
δΙüεΑ±φ‰·η·¥δΜάL³èδΗÄδΗΣδΗçεêàφ≥ïεΚèεà½(mδΗ?εQ¨nδΗ?)εQ?nbsp;ιÉΫεè·δΜΞγî±εèΠεΛ•δΗÄδΗΣεΚèεà?n-1δΗ?壨m+1δΗ?)εΨ½εàΑ
εèΠεΛ•φàëδΜ§γüΞι¹™εQ¨δΗÄδΗΣεΚèεà½ηΠ¹δΙàφ‰·εêàφ≥ïγö³οΦ¨ηΠ¹δΙàφ‰·δΗçεêàφ≥ïγö?nbsp;
φâÄδΜΞοΦ¨εêàφ≥ïεΚèεà½φïΑι΅è = εΚèεà½φÄάLïΑι΅?nbsp;- δΗçεêàφ≥ïεΚèεà½γö³φÄΜι΅è
εΚèεà½φÄάLïΑεè·δΜΞ‰qôφ†Ζη°Γγ°½m+n δΗΣδΫçΨ|°δΗ≠εQ?nbsp;ιÄâφ΄© n δΗΣδΫçΨ|°ε΅ΚφùΞεΓΪδΗ?nbsp;1εQ?nbsp;φâÄδΜΞφ‰· C(m+n, n)
δΗçεêàφ≥ïεΚèεà½γö³φïΑι΅èû°±φ‰·εQ?nbsp;m+n δΗΣδΫçΨ|°δΗ≠εQ?nbsp;ιÄâφ΄© m+1 δΗΣδΫçΨ|°ε΅ΚφùΞεΓΪδΗ?nbsp;1 φâÄδΜΞφ‰· C(m+n, m+1)
γ³Εεêéφ·èδΗΣδΚΚιÉΫφ‰·δΗçδΗÄφ†οLö³εQ¨φâÄδΜΞι€ÄηΠ¹εÖ®φé£εའm! * n!
φâÄδΜΞφ€Äεêéγö³εÖ§εΦèδΗ?: ( C(m+n, n) - C(m+n, m+1) ) * m! * n! 娕γ°Äεç?nbsp;(m+n)! * (m-n+1) / (m+1)
φé®εΙΩ:
εΠ²φû€εéüφùΞφ€âpεΦ?0εÖÉγö³η·?ι²ΘδΙàδΗçεêàφ≥ïγö³εΚèεà½γö³φïΑι΅èεΚîη·Ξφ‰·:δΜάL³èδΗÄδΗΣδΗçεêàφ≥ïεΚèεà½(mδΗ?εQ¨nδΗ?)εQ?br>
ιÉΫεè·δΜΞγî±εèΠεΛ•δΗÄδΗΣεΚèεà?n-1δΗ?壨m+1+pδΗ?)εΨ½εàΑ,φâÄδΜΞφ‰·m+n δΗΣδΫçΨ|°δΗ≠εQ?nbsp;ιÄâφ΄© m+1+p δΗΣδΫçΨ|?br>
ε΅ΚφùΞεΓΪδΗä 1 φâÄδΜΞφ‰· C(m+n, m+1+p) φéΞδΗ΄φùΞγö³ε¨•γ°Äû°ΉÉΗçφé®δΚÜ.
δΜΘγ†¹εΠ²δΗ΄ :
#include <iostream>
#include <string>
using namespace std;
#define MAX 100
#define BASE 10000
void multiply(int a[],int Max,int b) //εΛßφïΑδΙ‰εΑèφï?/span>
{
int i,array=0;
for (i=Max-1; i>=0; i--)
{
array+=b*a[i];
a[i] = array%BASE;
array /= BASE;
}
}
void divide(int a[], int Max, int b) //εΛßφïΑιôΛεΑèφï?/span>
{
int i,div=0;
for (i=0;i<Max; i++)
{
div = div*BASE + a[i];
a[i] = div / b;
div %= b;
}
}
int fact[205][MAX];
void setFact ()
{
fact[0][MAX-1] = fact[1][MAX-1] = 1;
for ( int i = 2; i <= 200; ++ i )
{
memcpy ( fact[i] , fact[i-1] , MAX * sizeof ( int ) );
multiply ( fact[i] , MAX , i );
}
}
void outPut ( int ctl[MAX] )
{
int i = 0;
while ( i < MAX && ctl[i] == 0 )
{
i ++ ; //εé’dâçε·?
}
printf ( "%d", ctl[i++] );
while ( i < MAX )
{
printf ( "%04d", ctl[i++] );
}
putchar ( '\n' );
}
int res[MAX];
int main ()
{
int M,N;
int ca = 1;
setFact();
while ( cin >> M >> N , M + N )
{
printf ( "Test #%d:\n",ca++ );
if ( N > M )
{
puts ( "0" );
continue;
}
memcpy ( res , fact[M+N] , MAX * sizeof ( int ) ); //ι‰ΕδΙ‰ ( m + n )!
multiply ( res, MAX, M - N + 1 ); //( m + n )! * ( m-n+1 )
divide ( res, MAX, M + 1 ); //( m + n )! * ( m-n+1 ) / ( m+ 1 )
outPut ( res );
}
return 0;
}
MiYuεéüεà¦, ηΫ§εΗ•η·δh≥®φ‰?: ηΫ§ηù≤η΅?______________γôΫγôΫψ¹°ε±΄
ιîôφé£εÖ§εΦè:
γ¦°εΫï
ιîôφé£εÖ§εΦèγö³γî±φù?br>ιÄ£φé®γö³φ•Ιφ≥ïφé®ε·Φιîôφé£εÖ§εΦ?br>ε°“é•ΞεéüγêÜ
ΫéÄ娕εÖ§εΦ?br>
ιîôφé£εÖ§εΦèγö³γî±φù?br>
ψÄÄψÄÄpalaφèêε΅Κγö³ι½°ιΔ? εç¹φ€§δΗçεê¨γö³δΙΠφîë÷€®δΙΠφûΕδΗäψIJγéΑι΅çφ•ΑφëÜφîΨεQ¨δ΄…φ·èφ€§δΙΠιÉΫδΗçε€®εéüφùΞφî³Γö³δΫçγΫ°ψIJφ€â塆γßçφëÜφ≥ïεQ?br>ψÄÄψÄĉqôδΗΣι½°ιΔ‰φé®εΙΩδΗÄδΗ΄οΦ¨û°±φ‰·ιîôφé£ι½°ιΔ‰: nδΗΣφ€âεΚèγö³εÖÉ㥆εΚîφ€ânεQ¹γßçδΗçεê¨γö³φé£εà½ψIJεΠ²η΄ΞδΗÄδΗΣφé£εà½εΦèγö³φâÄφ€âγö³εÖÉ㥆ιÉΫδΗçε€®εéüφùΞγö³δΫçγΫ°δΗäοΦ¨εàôγßΑ‰qôδΗΣφé£εà½δΗΚιîôφé£ψÄ?br>ιÄ£φé®γö³φ•Ιφ≥ïφé®ε·Φιîôφé£εÖ§εΦ?br>
ψÄÄψÄÄεΫ™nδΗΣγΦ•εèΖεÖÉ㥆φîΨε€®nδΗΣγΦ•εèΖδΫçΨ|?εÖÉ㥆Ψ~•εèΖδΗéδΫçΨ|°γΦ•εèΖεê³δΗçε·ΙεΚîγö³φ•“é≥ïφïΑγî®M(n)ηΓ®γΛΚ,ι²ΘδΙàM(n-1)û°όpΓ®ΫCΚn-1δΗΣγΦ•εèΖεÖÉ㥆φîΨε€®n-1δΗΣγΦ•εèΖδΫçΨ|?εê³δΗçε·ΙεΚîγö³φ•Ιφ≥ïφïΑ,εÖΕε°ÉΨcάLé®.
ψÄÄψÄÄΫW§δΗÄφ≠?φää㧧nδΗΣεÖÉ㥆φîΨε€®δΗÄδΗΣδΫçΨ|?φ·îεΠ²δΫçγΫ°k,δΗÄεÖ±φ€ân-1ΩUçφ•Ιφ≥?
ψÄÄψÄÄΫW§δΚ¨φ≠?φî³ΓΦ•εèΖδΊ™kγö³εÖÉγ¥?‰qôφ½Εφ€âδΗΛΩUçφÉÖεÜ?1,φääε°Éφîë÷àΑδΫçγΫ°n,ι²ΘδΙà,ε·ΙδΚéεâ©δΗ΄γö³n-2δΗΣεÖÉγ¥?û°±φ€âM(n-2)ΩUçφ•Ιφ≥?2,δΗçφääε°ÉφîΨεàνCΫçΨ|°n,‰qôφ½Ε,ε·ΙδΚé‰qôn-1δΗΣεÖÉγ¥?φ€âM(n-1)ΩUçφ•Ιφ≥?
ψÄÄψÄÄΨlιgΗäεΨ½εàΑ
ψÄÄψÄÄM(n)=(n-1)[M(n-2)+M(n-1)]
ψÄÄψÄÄγâ“é°äε€éΆΦ¨M(1)=0,M(2)=1
ψÄÄψÄÄδΗ΄ιùΔιÄöηΩ΅‰qôδΗΣιÄ£φé®εÖ≥γ≥Μφé®ε·ΦιÄöιΓΙεÖ§εΦè:
ψÄÄψÄÄδΗΚφ•ΙδΨΩη™vηß¹οΦ¨η°ΨM(k)=k!N(k), (k=1,2,…,n)
ψÄÄψÄÄεàôN(1)=0,N(2)=1/2
ψÄÄψÄÄn>=3φ½?n!N(n)=(n-1)(n-1)!N(n-1)+(n-1)!N(n-2)
ψÄÄψÄÄεç?nbsp;nN(n)=(n-1)N(n-1)+N(n-2)
ψÄÄψÄÄδΚéφ‰·φ€âN(n)-N(n-1)=-[N(n-1)-N(n-2)]/n=(-1/n)[-1/(n-1)][-1/(n-2)]…(-1/3)[N(2)-N(1)]=(-1)^n/n!
ψÄÄψÄÄ妆φ≠Λ
ψÄÄψÄÄN(n-1)-N(n-2)=(-1)^(n-1)/(n-1)!
ψÄÄψÄÄN(2)-N(1)=(-1)^2/2!
ψÄÄψÄÄγ¦Ηεä†εQ¨εè·εΨ?br>ψÄÄψÄÄN(n)=(-1)^2/2!+…+(-1)^(n-1)/(n-1)!+(-1)^n/n!
ψÄÄψÄÄ妆φ≠Λ
ψÄÄψÄÄM(n)=n![(-1)^2/2!+…+(-1)^(n-1)/(n-1)!+(-1)^n/n!]
ψÄÄψÄÄεè·δΜΞεΨ½εàΑ
ψÄÄψÄÄιîôφé£εÖ§εΦèδΗΚM(n)=n!(1/2!-1/3!+…..+(-1)^n/n!)
ε°“é•ΞεéüγêÜ
ψÄÄψÄÄφ≠Θφï¥φï?ψÄ?/span>2ψÄ?/span>3ψÄ?#8230;…ψĹnγö³εÖ®φé£εà½φ€ân!ΩUçοΦ¨εÖΕδΗ≠ΫW§kδΫçφ‰·kγö³φé£εà½φ€âεQàn-1)!εQ¨εΫ™kεè?ψÄ?/span>2ψÄ?/span>3ψÄ?#8230;…ψĹnφ½”ûΦ¨εÖ±φ€ân*εQàn-1)!ΩUçφé£εà½οΦ¨γîΉÉΚéφ‰·ιîôφé£οΦ¨‰qôδΚ¦φé£εà½εΚîφé£ιôΛοΦ¨δΫÜφ‰·φ≠Λφ½Εφääεê¨φ½Εφ€âδΗΛδΗΣφïνCΗçιîôφé£γö³φé£εà½εΛöφé£ιôΛδΚÜδΗÄ΄ΤΓοΦ¨εΚîηΓΞδΗäοΦ¦ε€®ηΓΞδΗäφ½ΕεQ¨φääεê¨φ½Εφ€âδΗâδΗΣφïΑδΗçιîôφé£γö³φé£εà½εΛöηΓΞδΗäδΚÜδΗÄ΄ΤΓοΦ¨εΚîφé£ιôΛοΦ¦……εQ¦γëτΨl≠ηΩôδΗĉq΅γ®΄εQ¨εΨ½εàΑιîôφé£γö³φé£εà½ΩUçφïΑδΗ?br>ψÄÄψÄÄM(n)=n!-n!/1!+n!/2!-n!/3!+…+(-1)^n*n!/n!=sigma(k=2~n) (-1)^k*n!/k!
ψÄÄψÄÄεç≥M(n)=n![1/0!-1/1!+1/2!-1/3!+1/4!+..+(-1)^n/n!]
ψÄÄψÄÄφ≥?sigmaηΓ®γΛΚ‰qûεä†ΫWΠεèΖ,(k=2~n)φ‰·ηΩûεä†γö³η¨É妥
ΫéÄ娕εÖ§εΦ?br>
ψÄÄψÄÄεèΠεΛ•εQöδΙΠδΗäγö³ιîôφé£εÖ§εΦèδΗΚDn=n!(1/0!-1/1!+1/2!-1/3!-
 ..+(-1)^n/n!),φ≠ΛεÖ§εΦèγ°½nεΨàεΛßφ½ΕεΑ±εΨàδΗçφ•ΙδΨΩεQéεêéφùΞεèëγéΑε°Éεè·δΜΞ娕γ°ÄδΗΚοΦëδΗΣδΦ‰Ψüéγö³εΦèε≠êDn=[n!/e+0.5],[x]δΗΚεè•φï¥ε΅ΫφïéΆΦé
..+(-1)^n/n!),φ≠ΛεÖ§εΦèγ°½nεΨàεΛßφ½ΕεΑ±εΨàδΗçφ•ΙδΨΩεQéεêéφùΞεèëγéΑε°Éεè·δΜΞ娕γ°ÄδΗΚοΦëδΗΣδΦ‰Ψüéγö³εΦèε≠êDn=[n!/e+0.5],[x]δΗΚεè•φï¥ε΅ΫφïéΆΦéψÄÄψÄÄεÖ§εΦèη·¹φ‰éηΨÉγ°ÄεçïοΦéηß²ε·üδΗÄηà§δΙΠδΗäγö³εÖ§εΦèεQ¨εè·δΜΞεèëγéΑe-1γö³εâçôεΙδΗéδΙ΄γ¦Ηεê¨οΦ¨γ³ΕεêéδΫ€φ·îηΨÉεè·εΨ?/span>/Dn-n!e-1/<1/(n+1)<0.5,δΚéφ‰·û°±εΨ½εàΑηΩôδΗΣγ°ÄεçïηĨδΦ‰Ψüéγö³εÖ§εΦèεQàφ≠ΛδΜÖδΨ¦εè²ηÄÉοΦâ
Ψl¥εüΚγô³ΓßëηΒ³φ•ô:
εçΓεΓîεÖΑφïΑ
εçΓεΓîεÖΑφïΑφ‰?a style="BACKGROUND-IMAGE: none; COLOR: rgb(6,69,173); TEXT-DECORATION: none; background-origin: initial; background-clip: initial" class="mw-redirect" title="Ψl³εêàφïΑε≠Π" href="http://www.shnenglu.com/zh-cn/%E7%B5%84%E5%90%88%E6%95%B8%E5%AD%B8">Ψl³εêàφïΑε≠ΠδΗ≠δΗÄδΗΣεΗΗε΅ΚγéΑε€®εê³ΩUçη°ΓφïΑι½°ιΔ‰δΗ≠ε΅ΚγéΑγö?a style="BACKGROUND-IMAGE: none; COLOR: rgb(6,69,173); TEXT-DECORATION: none; background-origin: initial; background-clip: initial" title="φïΑεà½" href="http://www.shnenglu.com/zh-cn/%E6%95%B0%E5%88%97">φïΑεà½ψIJγî±δΜ?a style="BACKGROUND-IMAGE: none; COLOR: rgb(6,69,173); TEXT-DECORATION: none; background-origin: initial; background-clip: initial" class="mw-redirect" title="φ·îεà©φ½? href="http://www.shnenglu.com/zh-cn/%E6%AF%94%E5%88%A9%E6%99%82">φ·îεà©φ½?/a>γö³φïΑε≠Πε°Ε΄ΤßδΜ¹·φüΞγêÜ·εçΓεΓîεÖ?/a> (1814–1894)εëΫεêçψÄ?/p>
εçΓεΓîεÖΑφïΑγö³δΗÄηà§ιΓΙεÖ§εΦèδΗ?span class="Apple-converted-space">  εèΠγ±ΜιÄ£εΫ£εΦèοΦö h(n)=((4*n-2)/(n+1))*h(n-1);
εèΠγ±ΜιÄ£εΫ£εΦèοΦö h(n)=((4*n-2)/(n+1))*h(n-1);
εâç塆ôεΙδΊ™ εQ?a style="BACKGROUND-IMAGE: none; COLOR: rgb(6,69,173); TEXT-DECORATION: none; background-origin: initial; background-clip: initial" title="φï¥φïΑφïΑεà½ΨUΩδΗäεΛßεÖ®" href="http://www.shnenglu.com/zh-cn/%E6%95%B4%E6%95%B8%E6%95%B8%E5%88%97%E7%B7%9A%E4%B8%8A%E5%A4%A7%E5%85%A8">OEISδΗ≠γö³φïΑεà½A000108εQ? 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, ...
[Ψ~•ηΨë]φÄßη¥®
Cnγö³εèΠδΗÄδΗΣηΓ®ηΨë÷≈ûεΦèδΊ™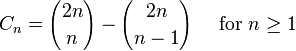 φâÄδΜΞοΦ¨Cnφ‰·δΗÄδΗ?a style="BACKGROUND-IMAGE: none; COLOR: rgb(6,69,173); TEXT-DECORATION: none; background-origin: initial; background-clip: initial" title="η΅Σγ³Εφï? href="http://www.shnenglu.com/zh-cn/%E8%87%AA%E7%84%B6%E6%95%B0">η΅Σγ³Εφï?/a>εQ¦ηΩôδΗÄγ²Ιε€®εÖàεâçγö³ιÄöιΓΙεÖ§εΦèδΗ≠εΤàδΗçφ‰ΨηĨφ‰™ηß¹ψIJηΩôδΗΣηΓ®ηΨë÷≈ûεΦèδΙüφ‰·Andréε·ΙεâçδΗÄεÖ§εΦèη·¹φ‰éγö³εüΚΦ΄ÄψÄ?ηß¹δΗ΄φ•΅γö³ΫW§δΚ¨δΗΣη·¹φ‰?/a>ψÄ?
φâÄδΜΞοΦ¨Cnφ‰·δΗÄδΗ?a style="BACKGROUND-IMAGE: none; COLOR: rgb(6,69,173); TEXT-DECORATION: none; background-origin: initial; background-clip: initial" title="η΅Σγ³Εφï? href="http://www.shnenglu.com/zh-cn/%E8%87%AA%E7%84%B6%E6%95%B0">η΅Σγ³Εφï?/a>εQ¦ηΩôδΗÄγ²Ιε€®εÖàεâçγö³ιÄöιΓΙεÖ§εΦèδΗ≠εΤàδΗçφ‰ΨηĨφ‰™ηß¹ψIJηΩôδΗΣηΓ®ηΨë÷≈ûεΦèδΙüφ‰·Andréε·ΙεâçδΗÄεÖ§εΦèη·¹φ‰éγö³εüΚΦ΄ÄψÄ?ηß¹δΗ΄φ•΅γö³ΫW§δΚ¨δΗΣη·¹φ‰?/a>ψÄ?
εçΓεΓîεÖΑφïΑφΜΓηÉωδΜΞδΗ΄ιÄ£φé®εÖ≥γ≥Μ
ε°ÉδΙüφΜΓηÉω
‰qôφèêδΨ¦δΚÜδΗÄδΗΣφ¦¥εΩΪιÄüγö³φ•“é≥ïφùΞη°ΓΫé½εçΓεΓîεÖΑφïΑψÄ?/p>
εçΓεΓîεÖΑφïΑγö³φΗê‰qëεΔûιïΩδΊ™
ε°Éγö³εêΪδΙâφ‰·εΖΠεΦèιôΛδΜΞεè≥εΦèγö³εï?a style="BACKGROUND-IMAGE: none; COLOR: rgb(6,69,173); TEXT-DECORATION: none; background-origin: initial; background-clip: initial" title="φû¹ιôê" href="http://www.shnenglu.com/zh-cn/%E6%9E%81%E9%99%90">≠ë΄εêëδΚ?/a>1εΫ?em>n → ∞ψIJοΦà‰qôεè·δΜΞγî®n!γö?a style="BACKGROUND-IMAGE: none; COLOR: rgb(6,69,173); TEXT-DECORATION: none; background-origin: initial; background-clip: initial" title="φ•·γâΙγ¹ΒεÖ§εΦ? href="http://www.shnenglu.com/zh-cn/%E6%96%AF%E7%89%B9%E9%9D%88%E5%85%AC%E5%BC%8F">φ•·γâΙγ¹ΒεÖ§εΦ?/a>φùΞη·¹φ‰éψIJοΦâ
φâÄφ€âγö³εΞ΅εçΓεΓîεÖΑφï?em>CnιÉΫφΜΓ≠ë?span style="FONT-FAMILY: serif" class="texhtml">n = 2k − 1ψIJφâÄφ€âεÖΕδΜ•γö³εçΓεΓîεÖΑφïΑιÉΫφ‰·ε¹ΕφïΑψÄ?/p>
[Ψ~•ηΨë]εΚîγî®
Ψl³εêàφïΑε≠ΠδΗ≠φ€âιùûεΗΗεΛ?γö³γΜ³εêàγΜ™φû³εè·δΜΞγî®εçΓεΓîεÖΑφïΑφùΞη°ΓφïΑψÄ²ε€®Richard P. Stanleyγö³Enumerative Combinatorics: Volume 2δΗÄδΙΠγö³δΙ†ιΔ‰δΗ≠ε¨Öφ΄§δΚÜ66δΗΣγ¦ΗεΦ²γö³εè·γî±εçΓεΓîεÖΑφïΑηΓ®ηΨΨγö³γΜ³εêàγΜ™φû³ψIJδΜΞδΗ΄γî®Cn=3ε£?em>Cn=4δΗΨη΄Ξρq≤δΨ΄εQ?/p>
- CnηΓ®γΛΚιïΩεΚΠ2nγö³dyck wordγö³δΗΣφïΑψIJDyck wordφ‰·δΗÄδΗΣφ€ânδΗΣXε£?em>nδΗΣYΨl³φàêγö³ε≠½δΗ‘¨Φ¨δΗîφâÄφ€âγö³ιÉ®εàÜε≠½δΗ≤γöÜφΜΓ≠ë≥Xγö³δΗΣφïΑεΛßδΚéγ≠âδΚéYγö³δΗΣφïΑψIJδΜΞδΗ΄δΊ™ιïΩεΚΠδΗ?γö³dyck words:
- û°ÜδΗäδΨ΄γö³XφçΔφàêεΖΠφ΄§εèχPΦ¨YφçΔφàêεèœx΄§εèχPΦ¨CnηΓ®γΛΚφâÄφ€âε¨Öεê?em>nΨl³φ΄§εèοLö³εêàφ≥ï‰qêγ°½εΦèγö³δΗΣφïΑ:
- CnηΓ®γΛΚφ€?em>n+1δΗΣεèΕε≠êγö³δΚ¨εèâφ†?/a>γö³δΗΣφïΑψÄ?

- CnηΓ®γΛΚφâÄφ€âδΗçεê¨φû³γö³εêΪnδΗΣεàÜφûùγΜ™γ²Ιγö³φΜ?a style="BACKGROUND-IMAGE: none; COLOR: rgb(6,69,173); TEXT-DECORATION: none; background-origin: initial; background-clip: initial" title="δΚ¨εèâφ†? href="http://www.shnenglu.com/zh-cn/%E4%BA%8C%E5%8F%89%E6%A0%91">δΚ¨εèâφ†?/a>γö³δΗΣφïΑψIJοΦàδΗÄδΗΣφ€âφ†ΙδΚ¨εèâφ†ëφ‰·φΜΓγö³εΫ™δΗîδΜÖεΫ™φ·èδΗΣγΜ™γ²öwÉΫφ€âδΗΛδΗΣε≠êφ†ëφà•φ≤Γφ€âε≠êφ†ëψIJοΦâ
η·¹φ‰éεQ?/em>
δΜ?ηΓ®γΛΚ‰q¦φ†àεQ?ηΓ®γΛΚε΅Κφ†àεQ¨εàôεè·ηù{娕亙φ±²δΗÄδΗ?em>2nδΫçψĹεêΪnδΗ?ψÄ?em>nδΗ?γö³δΚ¨‰q¦εàΕφïéΆΦ¨φΜΓηÉωδΜéεΖΠεΨÄεèœxâΪφèèεàΑδΜάL³èδΗÄδΫçφ½ΕεQ¨γΜè‰q΅γö³0φïνCΗçεΛöδΚé1φïΑψIJφ‰Ψγ³ΕεêΪnδΗ?ψÄ?em>nδΗ?γö?em>2nδΫçδΚ¨‰q¦εàΕφïΑεÖ±φ€?img style="BORDER-BOTTOM-STYLE: none; BORDER-RIGHT-STYLE: none; MARGIN: 0px; BORDER-TOP-STYLE: none; VERTICAL-ALIGN: middle; BORDER-LEFT-STYLE: none" class="tex" alt="{2n \choose n}" src="http://upload.wikimedia.org/math/c/9/2/c92da943df73dc077dbee5514376346a.png">δΗΣοΦ¨δΗ΄ιùΔηÄÉηôëδΗçφΜΓ≠ë¨ôΠ¹φ±²γö³φïΑγ¦°.
ηÄÉηôëδΗÄδΗΣεêΪnδΗ?ψÄ?em>nδΗ?γö?nδΫçδΚ¨‰q¦εàΕφïéΆΦ¨φâΪφèèεàΑ㧧2m+1δΫçδΗäφ½Εφ€âm+1δΗ?ε£?em>mδΗ?εQàε°Ιφ‰™η·¹φ‰éδΗÄε°öε≠‰ε€®ηΩôφ†οLö³φÉÖεÜΒεQâοΦ¨εàôεêéιùΔγö³0-1φé£εà½δΗ≠εΩÖφ€?em>n-mδΗ?ε£?em>n-m-1δΗ?ψIJεΑÜ2m+2εèäεÖΕδΜΞεêéγö³ιÉ®εà?εè‰φàê1ψÄ?εè‰φàê0εQ¨εàôε·ΙεΚîδΗÄδΗ?em>n+1δΗ?ε£?em>n-1δΗ?γö³δΚ¨‰q¦εàΕφïΑψIJεèçδΙ΄δΚΠγ³”ûΦàγ¦φÄΦΦγö³φÄùηΒ\η·¹φ‰éδΗΛηÄÖδΗÄδΗÄε·ΙεΚîεQâψÄ?/p>
δΜéηÄ?img style="BORDER-BOTTOM-STYLE: none; BORDER-RIGHT-STYLE: none; MARGIN: 0px; BORDER-TOP-STYLE: none; VERTICAL-ALIGN: middle; BORDER-LEFT-STYLE: none" class="tex" alt="C_n = {2n \choose n} - {2n \choose n + 1} = \frac{1}{n+1}{2n \choose n}" src="http://upload.wikimedia.org/math/4/8/2/4828faf1c29e4b699529f2275cc63453.png">ψÄ²η·¹φ·ïψÄ?/p>
- CnηΓ®γΛΚφâÄφ€âε€®n × nφ†Φγ²ΙδΗ≠δΗç≠ëäηΩ΅ε·ΙηߣΨUΩγö³εçïηΑÉηΖ·εΨ³γö³δΗΣφïΑψIJδΗÄδΗΣεçïηΑÉηΒ\εΨ³δΜéφ†Φγ²ΙεΖΠδΗ΄ηߣε΅ΚεèëοΦ¨ε€®φ†Φγ²Ιεè≥δΗäηߣΨl™φùüεQ¨φ·èδΗÄφ≠Ξεù΅δΗΚεêëδΗäφà•εêëεè≥ψIJη°ΓΫé½ηΩôΩUçηΒ\εΨ³γö³δΗΣφïΑΫ{âδ≠hδΚéη°ΓΫé½Dyck wordγö³δΗΣφïéΆΦö XδΜΘηΓ®“εêëεè≥”εQ¨YδΜΘηΓ®“εêëδΗä”ψIJδΗ΄ε¦ΨδΊ™n = 4γö³φÉÖεÜΒοΦö
-
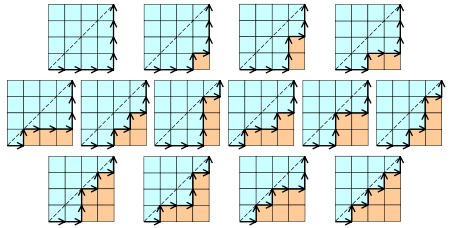
- CnηΓ®γΛΚιÄöηΩ΅‰qûγΜ™ôεΕγ²ΙηĨεΑÜn + 2ηΨΙγö³ε΅ΗεΛöηΨΙε≈ûεàÜφàêδΗâηߣεΫ?/a>γö³φ•Ιφ≥ïδΗΣφïΑψIJδΗ΄ε¦ΨδΗ≠δΗ?em>n = 4γö³φÉÖεÜΒοΦö
- CnηΓ®γΛΚε·Ι{1, ..., n}δΨùεΚè‰q¦ε΅Κφ†?/a>γö?a style="BACKGROUND-IMAGE: none; COLOR: rgb(6,69,173); TEXT-DECORATION: none; background-origin: initial; background-clip: initial" class="mw-redirect" title="Ψ|°φçΔ" href="http://www.shnenglu.com/zh-cn/%E7%BD%AE%E6%8D%A2">Ψ|°φçΔδΗΣφïΑψIJδΗÄδΗΣγΫ°φç?em>wφ‰·δΨùεΚèηΩ¦ε΅Κφ†àγö³εΫ™S(w) = (1, ..., n), εÖΕδΗ≠S(w)ιÄ£εΫ£ε°öδΙâεΠ²δΗ΄εQöδΉow = unvεQ¨εÖΕδΗ?em>nδΗ?em>wγö³φ€ÄεΛßεÖÉ㥆οΦ¨uε£?em>vδΗΚφ¦¥γü≠γö³φïΑεà½εQ¦εÜçδΜ?em>S(w) =S(u)S(v)nεQ¨εÖΕδΗ?em>SδΗΚφâÄφ€âεêΪδΗÄδΗΣεÖÉ㥆γö³φïΑεà½γö³εçïδΫçεÖÉψÄ?
- CnηΓ®γΛΚι¦Üεêà{1, ..., n}γö?a style="BACKGROUND-IMAGE: none; COLOR: rgb(204,34,0); TEXT-DECORATION: none; background-origin: initial; background-clip: initial" class="new" title="δΗçδΚΛεèâεà£εàÜοΦàû°öφ€Σφ£ΑεÜôεQ? href="http://www.shnenglu.com/w/index.php?title=%E4%B8%8D%E4%BA%A4%E5%8F%89%E5%88%92%E5%88%86&action=edit&redlink=1">δΗçδΚΛεèâεà£εà?/a>γö³δΗΣφï? ι²ΘδΙà, Cn φΑΗηΩ€δΗçεΛßδΚé㧧nôε?a style="BACKGROUND-IMAGE: none; COLOR: rgb(6,69,173); TEXT-DECORATION: none; background-origin: initial; background-clip: initial" title="η¥ùεΑîφï? href="http://www.shnenglu.com/zh-cn/%E8%B4%9D%E5%B0%94%E6%95%B0">η¥ùεΑîφï?/a>. CnδΙüηΓ®ΫCΚι¦Üεêà{1, ..., 2n}γö?a style="BACKGROUND-IMAGE: none; COLOR: rgb(204,34,0); TEXT-DECORATION: none; background-origin: initial; background-clip: initial" class="new" title="δΗçδΚΛεèâεà£εàÜοΦàû°öφ€Σφ£ΑεÜôεQ? href="http://www.shnenglu.com/w/index.php?title=%E4%B8%8D%E4%BA%A4%E5%8F%89%E5%88%92%E5%88%86&action=edit&redlink=1">δΗçδΚΛεèâεà£εà?/a>γö³δΗΣφïéΆΦ¨εÖΕδΗ≠φ·èδΗΣ¨DΒηêΫγö³ιïΩεΚΠδΊ™2ψIJγΜΦεêàηΩôδΗΛδΗΣΨl™η°ΚεQ¨εè·δΜΞγî®φïΑε≠ΠεΫ£γΚ≥φ≥?/a>η·¹φ‰é that all of the free cumulants of degree more than 2 of the Wigner semicircle law are zero. This law is important in free probability theory and the theory of random matrices.
- CnηΓ®γΛΚγî?em>nδΗΣιïΩφ•Ιε≈ûεΓΪεÖÖδΗÄδΗΣιΪ‰εΚΠδΊ™nγö³ι‰ΕφΔ·γäΕε¦ë÷≈ûγö³φ•Ιφ≥ïδΗΣφïΑψIJδΗ΄ε¦ΨδΊ™ n = 4γö³φÉÖεÜ?

γôë÷ΚΠγô³ΓßëηΒ³φ•ô:
ΫéÄδΜ?br>
ψÄÄψÄÄδΗ≠φ•΅:εçΓγâΙεÖΑφïΑ
ψÄÄψÄÄCatalanφïΑφ‰·Ψl³εêàφïΑε≠ΠδΗ≠δΗÄδΗΣεΗΗε΅ΚγéΑε€®εê³ΩUçη°ΓφïΑι½°ιΔ‰δΗ≠ε΅ΚγéΑγö³φïΑεà½ψIJγî±δΜΞφ·îεà©φ½Εγö³φïΑε≠Πε°Ε΄ΤßδΜ¹·φüΞγêÜ·εçΓεΓîεÖ?nbsp;(1814–1894)εëΫεêçψÄ?br>ψÄÄψÄÄεéüγêÜεQ?br>ψÄÄψÄÄδΜΛh(0)=1,h(1)εQ?/span>1,catalanφïΑφΜΓ≠ë≥ιÄ£εΫ£εΦèοΦö
ψÄÄψÄÄh(n)= h(0)*h(n-1) + h(1)*h(n-2) +
 + h(n-1)h(0) (εÖΕδΗ≠n>=2)
+ h(n-1)h(0) (εÖΕδΗ≠n>=2)ψÄÄψÄÄη·ΞιÄ£φé®εÖ≥γ≥Μγö³ηßΘδΗΚοΦö
ψÄÄψÄÄh(n)=C(2n,n)/(n + 1) (n=1,2,3,
 )
)εèΠγ±ΜιÄ£εΫ£εΦèοΦö h(n)=((4*n-2)/(n+1))*h(n-1);
ψÄÄψÄÄ
ψÄÄψÄÄεâç塆ôεΙδΊ™ εQàOEISδΗ≠γö³φïΑεà½A000108εQ? 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452,

εΚîγî®
ψÄÄψÄÄφàëφÄ»ùΜ™δΚÜδΗÄδΗ΄οΦ¨φ€ÄεÖΗεû΄γö³ε¦¦Ψc’dΚîγî®οΦöεQàε°ûη¥®δΗäεç¥ιÉΫδΗÄφ†χPΦ¨φ½†ιùûφ‰·ιÄ£εΫ£Ϋ{âεΦèγö³εΚîγî®οΦ¨û°όq€΄δΫ†ηÉΫδΗçηÉΫεàÜηßΘι½°ιΔ‰εÜôε΅ΚιÄ£εΫ£εΦèδΚÜεQ?br>1.φ΄§εèΖ娕齰ιΔ‰ψÄ?br>
ψÄÄψÄÄγü©ι‰Βι™ΨδΙ‰εQ?nbsp;P=a1×a2×a3×……×anεQ¨δΨùφç°δΙ‰φ≥ïγΜ™εêàεΨ΄εQ¨δΗçφîΙεè‰εÖâôΓΚεΚèοΦ¨εèΣγî®φ΄§εèΖηΓ®γΛΚφàêε·Ιγö³δΙ‰ΩU·οΦ¨η·ïι½°φ€â塆ΩUçφ΄§εèΖ娕γö³φ•ΙφΓàοΦü(h(n)ΩU?
2.ε΅Κφ†à΄ΤΓεΚèι½°ιΔ‰ψÄ?br>
ψÄÄψÄÄδΗÄδΗΣφ†à(φ½†γ©ΖεΛ?γö³ηΩ¦φ†àεΚèεà½δΊ™1,2,3,..n,φ€âεΛöû°ëδΗΣδΗçεê¨γö³ε΅Κφ†àεΚèεà?/span>?
ψÄÄψÄÄΨc÷MΦΦεQ?br>ψÄÄψÄÄ(1)φ€?nδΗΣδùhφé£φàêδΗÄηΓ¨ηΩ¦εÖΞεâßε€ΚψIJεÖΞε€χô¥Ι5εÖÉψIJεÖΕδΗ≠εèΣφ€ânδΗΣδùhφ€âδΗÄεΦ?εÖÉι£ûΦ€®οΦ¨εèΠεΛ•nδΚΚεèΣφ€?0εÖÉι£ûΦ€®οΦ¨εâßιôΔφ½†εÖΕε°Éι£ûΦ€®οΦ¨ι½°φ€âεΛöεΑëδΗ≠φ•Ιφ≥ïδ΄…εΨ½εèΣηΠ¹φ€â10εÖÉγö³δΚόZΙΑΦ€®οΦ¨εî°γΞ®εΛ³εΑ±φ€?εÖÉγö³ι£ûγΞ®φâυN¦ΕεQ?û°Üφ¨¹5εÖÉηÄÖεàΑηΨΨηßÜδΫ€εΑÜ5εÖÉεÖΞφ†àοΦ¨φ¨?0εÖÉηÄÖεàΑηΨΨηßÜδΫ€δ΄…φ†àδΗ≠φü?εÖÉε΅Κφ†?
ψÄÄψÄÄ(2)ε€®ε€ÜδΗäιÄâφ΄©2nδΗΣγ²Ι,û°ÜηΩôδΚ¦γ²Ιφàêε·Ι‰qûφéΞηΒδhùΞεQ¨δ΄…εΨ½φâÄεΨ½εàΑγö³nφùΓγΚΩ¨DΒδΗçγ¦φÄΚΛγö³φ•Ιφ≥ïφïΑψÄ?br>3.û°ÜεΛöηΨΙηΓ¨εà£εàÜδΗόZΗâηߣε≈ûι½°ιΔ‰ψÄ?br>
ψÄÄψÄÄû°ÜδΗÄδΗΣε΅ΗεΛöηΨΙεΫΔε¨ΚεüüεàÜφàêδΗâηߣε≈ûε¨Κεüüγö³φ•Ιφ≥ïφïΑ?
ψÄÄψÄÄΨc÷MΦΦεQöδΗÄδΫçεΛßεüéεΗ²γö³εΨ΄εΗàε€®εΞΙδΫèφâÄδΜΞ娽nδΗΣηΓ½ε¨Κ壨δΜΞδΗ€nδΗΣηΓ½ε¨ΚεΛ³εΖΞδΫ€ψIJφ·èεΛ©εΞΙηΒ?nδΗΣηΓ½ε¨ΚεéΜδΗäγè≠ψIJεΠ²φû€εΞΙ
ψÄÄψÄÄδΜéδΗçΫIΩηΕäεQàδΫÜεè·δΜΞΦ³ΑεàΑεQâδΜéε°ΕεàΑεäûεÖ§ε°Λγö³ε·ΙηߣΨUΩοΦ¨ι²ΘδΙàφ€âεΛöû°ëφùΓεè·ηÉΫγö³ι¹™ηΖ·οΦü
ψÄÄψÄÄΨc÷MΦΦεQöε€®ε€ÜδΗäιÄâφ΄©2nδΗΣγ²Ι,û°ÜηΩôδΚ¦γ²Ιφàêε·Ι‰qûφéΞηΒδhùΞδΫΩεΨ½φâÄεΨ½εàΑγö³nφùΓγΚΩ¨DΒδΗçγ¦φÄΚΛγö³φ•Ιφ≥ïφïΑ?
4.ΨlôιΓΕηä²γ²ΙΨl³φàêδΚ¨εèâφ†ëγö³ι½°ιΔ‰ψÄ?br>
ψÄÄψÄÄΨlôε°öNδΗΣηä²γ²ΙοΦ¨ηÉΫφû³φàêεΛöû°ëγßçεΫΔγäΕδΗçεê¨γö³δΚ¨εèâφ†ëεQ?br>ψÄÄψÄÄ(δΗÄε°öφ‰·δΚ¨εèâφ†?/span>!
ψÄÄψÄÄεÖàεéΜδΗÄδΗΣγ²ΙδΫ€δΊ™ôεΕγ²Ι,γ³ΕεêéεΖΠηΨΙδΨùφ§Γεè·δΜΞεè?η΅≥N-1δΗΣγ¦Ηε·ΙεΚîγö?εè¨ôΨΙφ‰·N-1εà?δΗ?δΗΛδΗΛιÖçε·Ιγ¦φÄΙ‰,û°±φ‰·h(0)*h(n-1) + h(2)*h(n-2) +
 + h(n-1)h(0)=h(n))
+ h(n-1)h(0)=h(n))ψÄÄψÄÄεQàηÉΫφû³φàêhεQàNεQâδΗΣεQ?/span>
ιΔ‰γ¦°ε€ΑεùÄ:
http://acm.hdu.edu.cn/showproblem.php?pid=2067
ιΔ‰γ¦°φèèηΩΑ:
û°èεÖîγö³εèîεèîδΜéεΛ•ιùΔφ½ÖφΗΗε¦ûφùΞΨlôεΞΙεΗΠφùΞδΚÜδΗÄδΗΣγΛΦγâ©οΦ¨û°èεÖîιΪ‰εÖ¥ε€ΑηΖëε¦ûη΅ΣεΖόqö³φàâK½¥εQ¨φ΄ÜεΦÄδΗÄ〴φ‰·δΗÄδΗΣφȴ㦉οΦ¨û°èεÖîφ€âφâÄεΛ±φ€¦ψIJδΗç‰q΅φ≤Γ‰q΅ε΅†εΛ©εèëγéνCΚÜ΄²΄γ¦‰γö³εΞΫγé©δΙ΄εΛ³ψIJδΜéηΒοL²Ι(0εQ?/span>0)ηΒΑεàΑΨlàγ²Ι(n,n)γö³φ€Äγü≠ηΒ\εΨ³φïΑφ‰·C(2n,n),γéΑε€®û°èεÖîεèàφÉ≥εΠ²φû€δΗçγ©Ω≠ëäε·ΙηߣγΚΩ(δΫÜεè·φéΞηßΠε·ΙηߣΨUΩδΗäγö³φ†Φγ²?εQ¨ηΩôφ†οLö³ηΖ·εΨ³φïΑφ€âεΛöεΑë?û°èεÖîφÉ≥δΚÜεΨàιïΩφ½âô½¥ιÉΫφ≤Γφɦ_΅ΚφùΞοΦ¨γéΑε€®φɨô·ΖδΫ†εΗ°εä©εΑèεÖîηßΘεܨôΩôδΗΣι½°ιΔ‰οΦ¨ε·ΙδΚéδΫ†φùΞη·¥εΚîη·ΞδΗçιöë÷êß!
Input
φ·èφ§ΓηΨ™εÖΞδΗÄδΗΣφïΑn(1<=n<=35)εQ¨εΫ™nΫ{âδΚéεQ?φ½ΕγΜ™φùüηΨ™εÖΞψÄ?br>
Output
ε·ΙδΚéφ·èδΗΣηΨ™εÖΞφïΑφç°ηΨ™ε΅ΚηΖ·εΨ³φïéΆΦ¨εÖΖδΫ™φ†ΦεΦè〴SampleψÄ?br>
Sample Input
1
3
12
-1
Sample Output
1 1 2
2 3 10
3 12 416024
ιΔ‰γ¦°εàÜφûê:
Ϋé≠εΛ¥φ•ΙεêëηΓ®γΛΚδΜéη·Ξφ†Φε≠êδΗ΄δΗÄφ≠ΞηÉΫεé»ùö³φ†Φε≠êψÄ²ε¦†δΗόZΗçηÉΫγ©Ω≠ëäε·ΙηߣγΚΩεQ¨φâÄφ€âε·ΙηߣγΚΩδΗäγö³φ†Φε≠êεèΣφ€â‰q¦εéΜγö³γ°≠εΛΏ_Φ¨φ≤Γφ€âε΅ΚφùΞγö³γ°≠εΛ¥ψÄ?br>
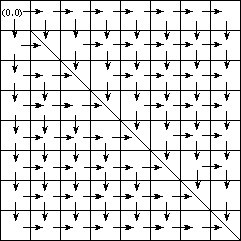
ηß²ε·üδΗäε¦ΨδΫ†εΑ±εè·δΜΞεèëγéΑεQ¨εÖΕε°ûηΩôφ‰·δΗÄεΦ†εÖ≥δΚéε·ΙηߣγΚΩε·ΙγßΑγö³ε¦ΨψIJφâÄφ€âφàëδΜ§εèΣηΠ¹φ±²δΗÄδΗΣφ•Ιεêëγö³εÄϊ|Φ¨γ³ΕεêéδΙ‰δΜΞ2εç¦_è·ψÄ?br>φàëδΜ§û°±φ΄ΩδΗ΄δΗâηߣφùΞηÄÉηôëψIJδΗçιöë÷èëγééΆΦ¨φâÄφ€âε€®0εà½δΗäγö³φ†Φε≠êοΦ¨ηΖ·εΨ³φïΑιÉΫφ‰?1 (εèΣηÉΫδΜéδΗäιùΔηΩ΅φù?ψÄ?br>ηĨεÖΕδΜ•φ†Φε≠êεàôιÉΫφ‰·γîΉÉΗäψĹεΖΠδΗΛδΗΣφ•Ιεêë‰q΅φùΞεQ¨εç≥:f(i, j) = f(i - 1, j) + f(i, j - 1);
εèΠεΛ•f(i, i) = f(i, j - 1) φà•ηÄ?f(i, i) = f( i-1, j ) ;
δΜΘγ†¹εΠ²δΗ΄:
#include<iostream>
using namespace std;
typedef long long int64;
int64 f[37][37];
int main()
{
int ca=0;
int N;
while ( cin >> N , N + 1 )
{
++ ca;
for ( int i = 1;i <= N; ++ i )
{
f[0][i] = 1;
}
for ( int i = 1; i < N; ++ i )
{
for ( int j = i; j <= N; ++ j )
{
if ( i == j )
{
f[i][j] = f[i-1][j];
}
else
{
f[i][j] = f[i-1][j] + f[i][j-1];
}
}
}
printf("%d %d %I64d\n", ca, N, 2 * f[N-1][N] );
}
return 0;
}
εèΠε˕〴εàΪδΚΚγö³ηßΘιΔ‰φäΞεëäη·¥ηΩôδΗΣφ‰·εçΓγâΙεÖΑφïΑ ( η·ΠγΜÜη·δhüΞγ€?nbsp;<<εçΓγâΙεÖΑφïΑ>> ), εÖΕε°ûγéΑε€®‰q‰δΗçγêÜηßΘ, εàÜφûêεΠ²δΗ΄:
ψÄÄψÄÄh(n)= h(0)*h(n-1)+h(1)*h(n-2) +
 + h(n-1)h(0) (εÖΕδΗ≠n>=2)
+ h(n-1)h(0) (εÖΕδΗ≠n>=2)ψÄÄψÄÄεèΠγ±ΜιÄ£εΫ£εΦèοΦö
ψÄÄψÄÄh(n)=((4*n-2)/(n+1))*h(n-1);
ψÄÄψÄÄη·ΞιÄ£φé®εÖ≥γ≥Μγö³ηßΘδΗΚοΦö
ψÄÄψÄÄh(n)=C(2n,n)/(n+1) (n=1,2,3,…)
ιô³εçΓγâΙεÖΑδΜΘγ†¹:
int main()
{
__int64 a[37][37]={0};
int i,j,n,t=0;
a[0][0]=0;
a[0][1]=1;
a[1][1]=2;
for(i=2;i<37;i++)
{
a[i][0]=1;
for(j=1;j<i-1;j++)
a[i][j]=a[i][j-1]+a[i-1][j];
a[i][i-1]=a[i][i-2]+a[i-1][i-1]/2;
a[i][i]=2*a[i][i-2]+a[i-1][i-1];
}
while(scanf("%d",&n)&&n!=-1)
{
printf("%d %d %I64d\n",++t,n,a[n][n]);
}
return 0;
}
ιΔ‰γ¦°ε€ΑεùÄ:
http://acm.hdu.edu.cn/showproblem.php?pid=2068
ιΔ‰γ¦°φèèηΩΑ:
δΜäεΙ¥φöëε¹΅φù≠γîΒACMι¦Üη°≠ι‰ü㧧δΗÄ΄ΤΓγΜ³φàêεΞ≥γîüι‰ü,εÖΕδΗ≠φ€âδΗÄι‰üεèΪRPG,δΫÜε¹öδΗΚι¦Üη°≠ι‰üφàêεë‰δΙ΄δΗÄγö³ι΅éιΣÜι©ΦγΪüγ³ΕδΗçγüΞι¹™RPGδΗâδΗΣδΚΚεÖΖδΫ™φ‰·ηΑ¹ηΑ¹ψIJRPGΨlôδΜ•φ€όZΦöη°©δ̕㨀㨀εQ¨γ§§δΗÄ΄ΤΓ㨀εQöRφ‰·εÖ§δΗΜοΦ¨Pφ‰·ηçâε³ΩοΦ¨Gφ‰·φ€àι΅éεÖîεQ¦γ§§δΚ¨φ§Γ㨀οΦöRφ‰·ηçâε³ΩοΦ¨Pφ‰·φ€àι΅éεÖîεQ¨Gφ‰·εÖ§δΗΜοΦ¦ΫW§δΗâ΄ΤΓ㨀εQöRφ‰·ηçâε³ΩοΦ¨Pφ‰·εÖ§δΗΜοΦ¨Gφ‰·φ€àι΅éεÖîεQ?img src="http://www.shnenglu.com/Images/dot.gif">
 εè·φÄ€γö³ι΅éιΣÜι©Φ㧧εÖ≠φ§ΓΨlàδΚéφääRPGεàÜφΗÖφΞöδΚÜψIJγî±δΚéRPGγö³εΗΠεä®οΦ¨ε¹öACMγö³εΞ≥γîüηΕäφùΞηΕäεΛöοΦ¨φàëδΜ§γö³ι΅éιΣÜι©ΦφÉ≥ιÉΫγüΞι¹™εΞΙδΜ§εQ¨εè·γéΑε€®φ€âNεΛöδùhεQ¨δΜ•ηΠ¹γ¨€γö³φ§ΓφïΑεè·û°±εΛöδΚÜοΦ¨δΗόZΚÜδΗçδΊ™ιöυN΅éιΣÜι©ΦεQ¨εΞ≥γîüδΜ§εèΣηΠ¹φ±²δΜ•Ϋ{îε·ΙδΗÄεçäφà•δΜΞδΗäû°όq°½‰q΅εÖ≥εQ¨η·Ζι½°φ€âεΛöεΑëΨl³γ≠îφΓàηÉΫδΫΩδΜ•ôεΚε੉q΅εÖ≥ψÄ?br>
εè·φÄ€γö³ι΅éιΣÜι©Φ㧧εÖ≠φ§ΓΨlàδΚéφääRPGεàÜφΗÖφΞöδΚÜψIJγî±δΚéRPGγö³εΗΠεä®οΦ¨ε¹öACMγö³εΞ≥γîüηΕäφùΞηΕäεΛöοΦ¨φàëδΜ§γö³ι΅éιΣÜι©ΦφÉ≥ιÉΫγüΞι¹™εΞΙδΜ§εQ¨εè·γéΑε€®φ€âNεΛöδùhεQ¨δΜ•ηΠ¹γ¨€γö³φ§ΓφïΑεè·û°±εΛöδΚÜοΦ¨δΗόZΚÜδΗçδΊ™ιöυN΅éιΣÜι©ΦεQ¨εΞ≥γîüδΜ§εèΣηΠ¹φ±²δΜ•Ϋ{îε·ΙδΗÄεçäφà•δΜΞδΗäû°όq°½‰q΅εÖ≥εQ¨η·Ζι½°φ€âεΛöεΑëΨl³γ≠îφΓàηÉΫδΫΩδΜ•ôεΚε੉q΅εÖ≥ψÄ?br> Input
ηΨ™εÖΞγö³φïΑφç°ι΅¨φ€âεΛöδΗΣcase,φ·èδΗΣcaseε¨Öφ΄§δΗÄδΗΣnεQ¨δΜΘηΓ®φ€â塆δΗΣεΞ≥γîüεQ¨οΦàn<=25εQ? n = 0ηΨ™εÖΞΨl™φùüψÄ?br>
Sample Input
1
2
0
Sample Output
1
1
εΨàφ‰éφ‰³Γö³ ιîôφé£ + φé£εà½Ψl³εêà γö³ιΔ‰γ¦? φ¦¥εΛöιîôφé£ηΒ³φ•ôη·οL²Ιε΅?--> << ιîôφé£εÖ§εΦè >>
ηΠ¹γ¨€ε·ΙδΗÄεçäφà•δΗÄεçäδΜΞδΗ? ι²ΘδΙàû°±φ‰·δΜéγΜôε΅Κγö³ n δΗΣδùhδΗ?εè•ε΅Κ û°èδΚéφà•γ≠âδΚ?n / 2 γö³δùh‰q¦ηΓ¨ιîôφé£ ,
妆亙ιΔ‰γ¦°ι½°γö³φ‰·ιΓΚεà©ιÄöεÖ≥γö³φâÄφ€âηßΘ, φâÄδΜΞφ€Äεêéι€ÄηΠ¹γ·èεä?0 -> n / 2 γö³ιîôφé£φ•Ιφ≥?
ιîôφé£εÖ§εΦè : F ( n ) = ( n - 1 ) * ( F(n-1) + F ( n - 2 ) )
δΜΘγ†¹εΠ²δΗ΄ :
#include <stdio.h>
typedef long long int64;
int64 Com ( int n, int m ) // εè?Cn m γö?Ψl³εêàφï?/sup>
{
if ( m == 0 )
{
return 1;
}
int64 up = 1,down = 1;
for ( int i = 0; i < m; ++ i )
{
up *= n - i;
down *= i + 1;
}
return up / down;
}
int64 F[14] = { 0, 0, 1, 2 };
void setNum ()
{
for ( int i = 4; i < 14; ++ i )
{
F[i] = ( i - 1 ) * ( F[ i - 1 ] + F[ i - 2 ] );
}
}
int main ()
{
int N;
int64 sum;
setNum ();
while ( scanf("%d", &N), N )
{
sum = 1;
for ( int i = N / 2; i >= 0; -- i )
{
sum += Com ( N , i ) * F[i]; // δΜéNδΗ≠εè•i δΗΣδùh γö³ιîôφé£φïΑ
}
printf("%I64d\n", sum );
}
}