算法介紹
計數排序是一個類似于桶排序的排序算法,其優勢是對已知數量范圍的數組進行排序。它創建一個長度為這個數據范圍的數組C,C中每個元素記錄要排序數組中對應記錄的出現個數。這個算法于1954年由 Harold H. Seward 提出。
當輸入的元素是 n 個 0 到 k 之間的整數時,它的運行時間是 Θ(n + k)。計數排序不是比較排序,排序的速度快于任何比較排序算法。
由于用來計數的數組C的長度取決于待排序數組中數據的范圍(等于待排序數組的最大值與最小值的差加上1),這使得計數排序對于數據范圍很大的數組,需要大量時間和內存。例如:計數排序是用來排序0到100之間的數字的最好的算法,但是它不適合按字母順序排序人名。但是,計數排序可以用在基數排序中的算法來排序數據范圍很大的數組。計數排序之所以能夠突破前面所述的Ω(nlgn)極限,是因為它不是基于元素比較的。計數排序適合所需排序的數組元素取值范圍不大的情況(范圍太大的話輔助空間很大)。
定理:任意一個比較排序算法在最壞情況下,都需要做Ω(nlgn)次比較。
算法的步驟如下:
- 找出待排序的數組中最大和最小的元素
- 統計數組中每個值為i的元素出現的次數,存入數組C的第i項
- 對所有的計數累加(從C中的第一個元素開始,每一項和前一項相加)
- 反向填充目標數組:將每個元素i放在新數組的第C(i)項,每放一個元素就將C(i)減去1
以下引自麻省理工學院算法導論——筆記:
Counting sort: No comparisons between elements.
• Input: A[1 . . n], where A[ j]??{1, 2, …, k} .
• Output: B[1 . . n], sorted.
• Auxiliary storage: C[1 . . k] .
Counting sort
for i ← 1 to k
do C[i] ← 0
for j ←1 to n
do C[A[ j]] ← C[A[ j]] + 1 —> C[i] = |{key = i}|
for i ← 2 to k
do C[i] ← C[i] + C[i–1] —>C[i] = |{key ← i}|
for j ← n downto 1
do B[C[A[ j]]] ← A[ j]
C[A[ j]] ← C[A[ j]] – 1
實例:
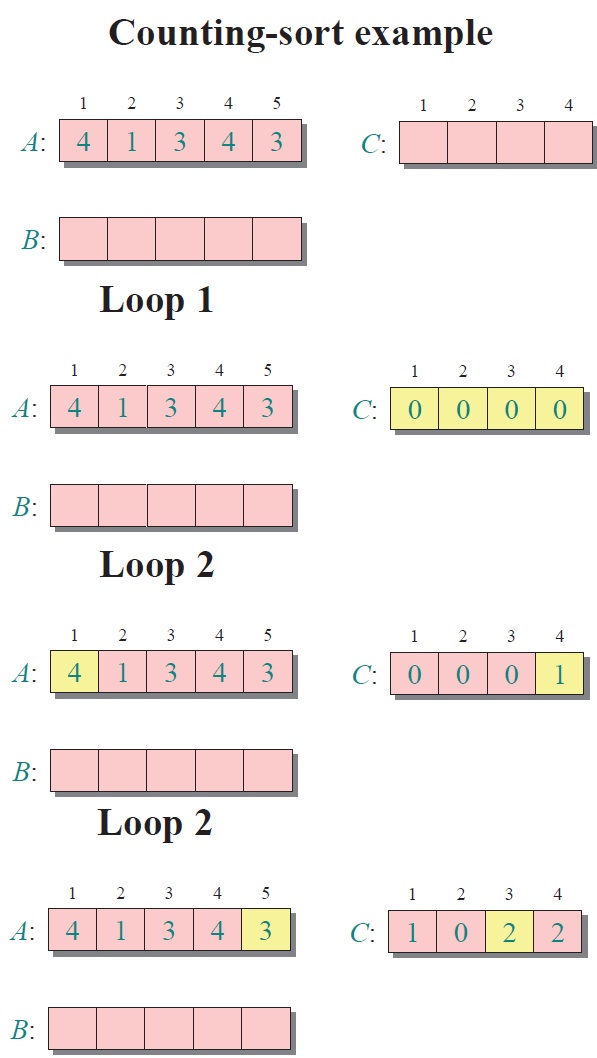
對所有的計數累加(從C中的第一個元素開始,每一項和前一項相加)
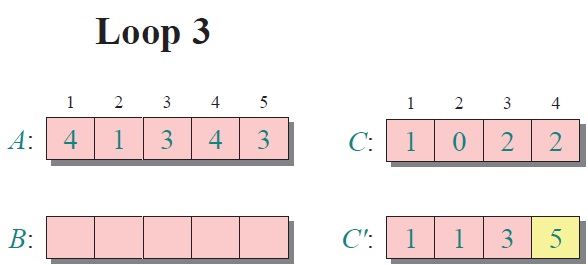
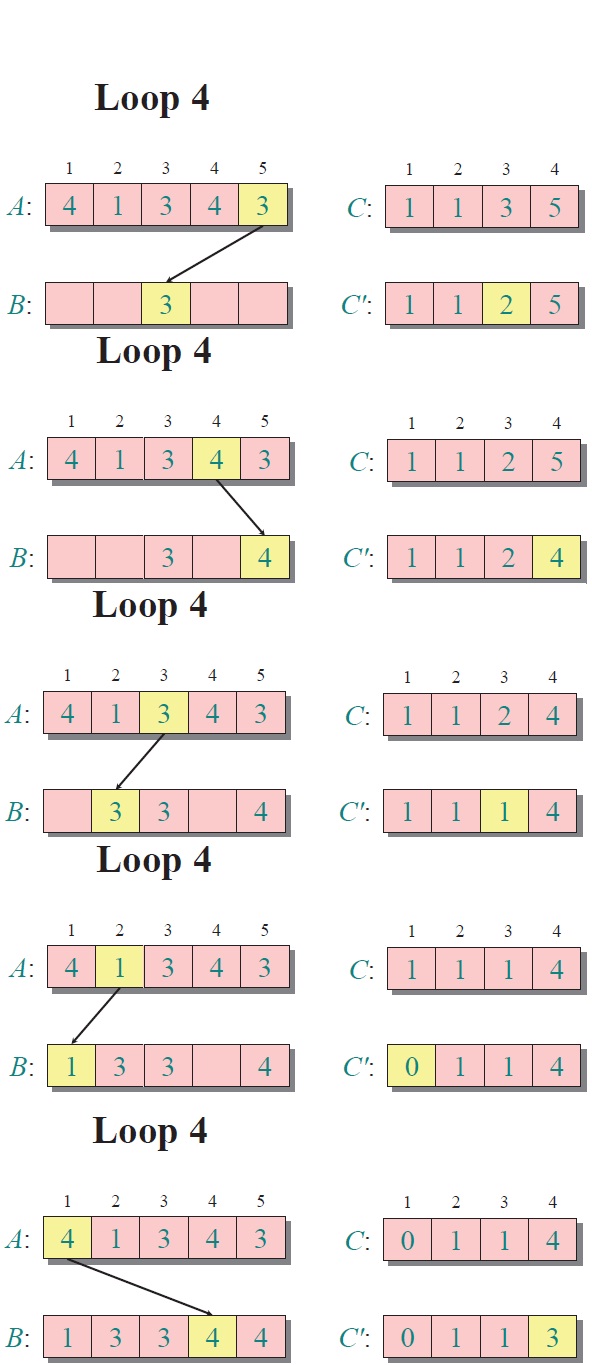
反向填充目標數組:將每個元素i放在新數組的第C(i)項,每放一個元素就將C(i)減去1


注:基于比較的排序算法的最佳平均時間復雜度為 O(nlogn)
穩定性:算法是穩定的。
如果k小于nlogn可以用計數排序,如果k大于nlogn可以用歸并排序。
代碼實例:
1 C++實現:
2 #include<cstdio>
3 #include<algorithm>
4 using namespace std;
5 //n為數組元素個數,k是最大的那個元素
6 void CountingSort(int *input, int size, int k){
7 int i;
8 int *result = new int[size]; //開辟一個保存結果的臨時數組
9 int *count = new int[k+1]; //開辟一個臨時數組
10 for(i=0; i<=k; ++i)
11 count[i]=0;
12 //使count[i]等于等于i的元素的個數
13 for(i=0; i<size; ++i)
14 ++count[input[i]]; //count數組中坐標為元素input[i]的增加1,即該元素出現的次數加1
15 for(i=1; i<=k; ++i)
16 count[i] += count[i-1];
17 for(i=size-1; i>=0; --i){ //正序來也行,但是到這來可以使排序是穩定的
18 --count[input[i]]; //因為數組下標從0開始,所以這個放在前面
19 result[count[input[i]]] = input[i]; //這個比較繞, count[input[i]-1] 就代表小于等于元素
}
20 copy(result,result+size,input); //調用copy函數把結果存回原數組
21 delete [] result; //記得釋放空間
22 delete [] count;
23 }
24 int main()
25 {
26 int input[11]={2,7,4,9,8,5,7,8,2,0,7};
27 CountingSort(input,11,9);
28 for(int i=0; i<11; ++i)
29 printf("%d ",input[i]);
30 putchar('\n');
31 return 0;
32 }
posted on 2012-11-13 11:07
王海光 閱讀(729)
評論(1) 編輯 收藏 引用 所屬分類:
算法