120 Archipelago 計算幾何:射線旋轉121 Bridges painting 圖論:染色問題122 The Book 圖論:哈密爾頓回路123 The Sum 遞推124 Broken Line 計算幾何:線段判交
125 shtirlits 搜索:深度優先搜索126 boxes 初等數論127 Telephone directory 排序128 Snake 排序 + HASH129 Inheritance 計算幾何:凸包+線段判交120 Archipelago 計算幾何:射線旋轉
題意:需要求一個正多邊形的N個點,但是給出的只有N和某兩個點的坐標。
題解:核心思想是根據給定的那兩個點的坐標確定多邊形中心點的坐標,這樣邊長也確定了,然后利用中心點到其中一個點的射線的旋轉求出所有的點坐標。
1) 正多邊形的中心點一定在任意兩個頂點的連線的中垂線上,然后根據已知點的相對關系,算出他們和中心點的夾角,利用這兩個條件就可以求出中心點的坐標了。
2) 然后就是要求某個點繞中心點旋轉360/N度后的坐標了,做N-1次旋轉操作就能求出所有的頂點了。旋轉可以通過解方程求解:
令原單位向量I,旋轉alpha角度后的單位向量Ia,其中I和alpha已知,Ix是我們需要求的。那么有以下兩個方程:
1) I.x * Ia.x + I.y * Ia.y = cos( alpha )
2) Ia.x2 + Ia.y2 = 1
將1)中的Ia.x用Ia.y表示代入方程2),利用一元二次求根公式可以求得兩個解,然后算出Ia.x,但是解肯定只有一個,可以用叉乘關系排除掉另外一個解。
121 Bridges painting
圖論:DFS構造
題意:對于一個圖,給定它的邊和點,現在要求給邊染色(黑色或者白色)。問能不能構造一種染色方法,使得所有的度數大于1的點的邊都能有至少有一條邊為黑色、至少有一條邊為白色。
題解:首先考慮什么情況下是不可能染色成功的;如圖1所示,對于下面這個圖,每個點的頂點度數為2,所以從任意一條邊開始染色,相鄰邊必然為相反色,由于存在奇環,導致必然有一個點的兩條邊的顏色相同,染色失敗。
然后再來考慮怎么將這個圖挽救回來,其實這個圖失敗的點只有一個,如果在那個點上再加一條邊,那么整個圖貌似就可以認為染色成功了。
于是我們進一步考慮是不是度數為奇數的點造就了這一切:
度數 = 1,該點所在邊可以隨便染色;
度數 > 1,說明必然存在環;
如果是偶數環,那么經過一系列的交錯染色,最后必然能夠在該結點上收獲兩條顏色不一樣的邊;
如果是奇數環,在染色完畢后,必然還有一條邊未被染色(因為度數為奇數),可以大膽的將它染成不同的顏色;
所以對于度數為奇數的點,采用交錯染色,一定可以將圖染色成功;
如圖,可以對于所有奇度數頂點作為根進行一次dfs,按照編號順序進行深度優先遍歷,先遍歷到的是1號,標記為黑色,然后將它的第一個兒子標記為白色,遍歷完畢,將第二個兒子標記為黑色(交錯染色),即每次更換結點的時候就將顏色取反,當我們遍歷到邊6的時候發現7是一條后向邊,于是回到了根結點,完成遍歷。
利用同樣方法,將所有度數為奇數的點進行一次遍歷,然后再將度數為偶數的點進行相同的遍歷(因為可能這不是一個連通圖,所以如果度數為偶數的點所在的圖集合中有奇數環,如圖1的情況,那么必然無解)。
遍歷完畢,需要對每個點判斷是否存在不合法的頂點(邊數大于1,并且只有一種染色),如果合法,說明所有邊都被染色了,輸出解即可。
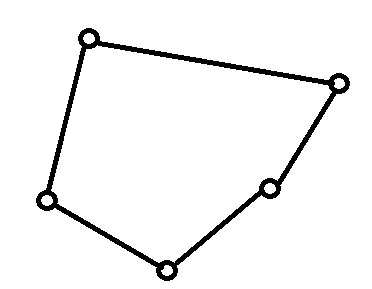
圖1
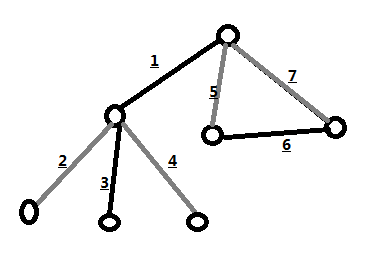
圖2
122 The book 哈密爾頓回路問題:Ore定理 + 構造
題意:給定N(N <= 1000)個點連成的圖,每個點度數大于等于(N+1)/2,求這個圖的一條哈密爾頓回路。
題解:
1)首先假設已經得到了一個環R(R的頂點個數為r),那么在未選到環內的點集R’中必然能夠找到某個點k和環R中其中一個點j有邊相連,假設沒有邊相連,那么環R和環外的點集R’互不連通,為兩個連通分量,和題意相左(因為每個點的度數大于等于(N+1)/2,圖論書上有證明,這肯定是一個連通圖,故不再累述),故R’中必然存在至少一個點k和R中點j相連,于是將那個點j連接到k上,這樣就變成了一個長度為r+1的鏈。
2)這個鏈的頭為s,尾為k,長度為r+1,不斷在剩下的點集中找點連接到s和k上,并且不斷更新s和k(連接到頭上,連接的點就變成了s,連接到尾上,連接的點就變成了k),直到找到一個極大連通子鏈(不能再在剩下的點中找到點連接到鏈的兩端了)。
3)由于k和剩下點集R’沒有點相連,所以我們只能在這條長鏈上找和k相連的點t(因為一定可以找到,為什么呢?k本身不就有個鏈內的點連著嘛,不然它就是個孤立點了)。所以找到(k , t)相連,并且(s, t+1) 相連,然后刪掉(t, t+1)這條邊,就能夠得到一個新的環了,如果此時環的長度為n就結束了,否則繼續1)。
圖3
123 The sum 遞推
題意:求斐波那契數列的第N(N <= 40)項。
題解:__int64數組預處理即可。
124 Broken line
計算幾何: 線段判交
題意:在平面上有一些閉合線段(沒有自交和相互交叉),判斷給定的點P是否在這個閉合線段內。
題解:其實就是判斷一個點是否在多邊形內;
首先,虛擬出一個無窮遠的點Q,然后用PQ和每個閉合線段去做相交檢測(兩線段判交在黑書上有詳盡的解釋,不再累述)。
1) 如果P在某條線段上,輸出BORDER;
2) 如果PQ和所有線段交點個數為奇數,說明在多邊形內,輸出INSIDE;
3) 如果PQ和所有線段交點個數為偶數,說明在多邊形外,輸出OUTSIDE;
125 Shtirlits
深度優先搜索 + 剪枝
題意:給定一個矩陣B (3X3),B[i][j]表示A[i][j]四周比它大的數的個數,求滿足條件的A。
題解:枚舉A[i][j]的每個數字,數字的范圍為 [0,9]。復雜度109,所以需要進行一定的剪枝。
a) 首先,可以肯定這B[i][j]中一定會至少有一個0,因為總有一個數沒有比它大的數(高處不勝寒啊~~)。對于B[i][j] == 0的格子,將A[i][j]設為最大值9一定不會錯,所以復雜度至少可以降到 108 了。
b) 將A的每個非9的格子標記為-1,然后對每個格子進行枚舉,枚舉范圍為 [ 0, 8 ], 因為B[i][j]為四周比它大的數的個數, 如果A[i][j]==9,那么B[i][j]必須為0,復雜度降至 98。
c) 每次枚舉完畢,進入下一個數的枚舉之前,進行全局的檢測,對于每個格子統計以下數據:
i) 已經枚舉的鄰居格子 H
ii) 總共有多少個鄰居格子 T
iii) 比自己大的鄰居格子 B
然后進行篩選,如果
x) 比當前格子大的鄰居數已經超出限定值, 即 B > B[i][j]
y) 比當前格子大的鄰居數 + 剩余未知鄰居數 < 給定比它大的鄰居數, 即 B + (T-H) < B[i][j]
均為無效解,無需往下枚舉,回溯。
d) 直到所有數枚舉完畢,輸出解即可。
126 Boxes
初等數論
題意:對于給定的A和B,
如果A > B, 則狀態變為 (A-B, 2*B)
如果A < B, 則狀態變為 (2*A, B-A)
當 A == B 時,結束。
要求輸出這個情況是否存在,如果存在輸出變換的次數,不存在輸出-1。
題解:根據題意,可以得出一些簡單的推論:
a) 當A == 0 或者 B == 0 時 答案為 0。
b) 最后A == B的時候,必定是K = (A+B)/2,所以當A+B為奇數時答案不存在。
c) 定義最后的狀態二元組為 (K, K),
倒數第二次的操作必定為 (3K/2,K/2) 或者(K/2,3K/2) (2種)
倒數第三次的操作必定為 (7K/4, K/4) 或者 (3K/4, 5K/4) 或者 (5K/4, 3K/4) 或者 (K/4, 7K/4) (4種)
倒數第四次操作(15K/8,K/8)... (8種)
倒數第i次操作 ( (2(i-1)-1)/2(i-1) * K, 1/2(i-1) * K ) ... (2(i-1) 種)
d) A和B的組合必定在這些情況中找。
于是定義 A = L1 / 2n * K, B = L2 / 2n * K (其中K = (A+B)/2, L1,L2為奇數,并且(L1+L2) = 2(n+1))
得:
L1 = 2n * (A/K)
L2 = 2n * (B/K)
令 A = 2a * A', K = 2k * K'
則有 L1 = 2(n+a-k) * A'/K' 為奇數,所以n+a-k = 0,并且要保證A' mod K' == 0,A 和 K 都為已知,則可以計算出 a 、A'、k、K',最終的步數就是k-a+1。
需要注意特殊情況:A或B為0的情況,以及A+B為奇數的情況。
127 Telephone directory
將所有電話號碼按首字母排序,統計每個首字母出現的次數Ai, Sum{ (Ai + K - 1 ) / K } + 2 就是答案。
128 Snake
想法題
題意:給定N(4<=N<=10000)個整數點,問能不能組出一個多邊形,滿足以下條件:
a) 閉合;
b) 所有的點都是多邊形上的點,并且只能被用一次;
c) 任何兩個連續的線段需要組成一個90度的直角;
d) 多邊形的所有邊都要平行于坐標軸;
e) 多邊形不能存在自交;
f) 多邊形的周長要滿足最小;
題解:
1) 對于輸入的點保存兩份數組PX、PY,并且記錄每個點在原數組的下標index;
2) 對PX進行X優先排序,對PY進行Y優先排序;
3) 對PX中序號為奇數的點PX[i]和它的下一個點PX[i+1]進行y值的判斷,如果這兩個點的y值不相等,那么說明這個點無法加入多邊形中(PX[i]無法配對,被孤立了),無解。否則PX[i].index和PX[i+1].index必然有一條邊(可以用鄰接表來存邊關系,因為最后求的是一個多邊形,所以每個點有且僅有兩條邊,其實就是一個哈密爾頓回路)。
并且加PX[i+1].x - PX[i].index 累加到答案ans中;
4) 對PY中的點作和3)一樣的處理,保存邊的關系,但是這里需要判斷一種自交的情況,如圖1中,3)操作完畢后,產生三條邊(1,1) - (2,1) (1,2) -(3, 2) (2,3) - (3,3);那么在進行操作4)的時候(1,1)-(1,2) 和 (3,2) - (3, 3)都是沒問題的,唯獨 (2,1) - (2,3) 和 先前的邊 (1,2) -(3, 2) 會產生自交,違反了e這條規則,所以需要檢測這種情況是否存在,如果存在,那么必然無解;具體檢測方法很多,不再累述;
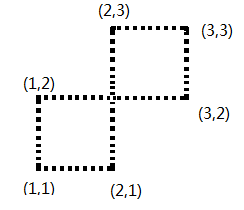
圖1
5) 進過3)和4)后,再進行一次連通性判斷即可,以防圖2的情況。

圖2
129 Inheritance
解析幾何 + 凸包 + 線段判交
題意:給定一個多邊形和若干線段,這個多邊形內任意兩點連線不會和多邊形邊界相交,分別求這些線段在多邊形內部的長度。
題解:首先,根據“多邊形內任意兩點連線不會和多邊形邊界相交”可以肯定這是個凸多邊形,于是問題就轉化成了求某條線段和凸多邊形相交后線段在多邊形內部分的長度。
由于給定的點是亂序的,所以最簡單的方法是求這些點集的一個凸包,構造出一個按點排序的多邊形,相鄰兩點連線為原多邊形的一條邊。
那么枚舉每條邊和給定線段的相交情況:
1) 不相交(平行),繼續判斷下一條邊;
2) 共線,直接跳出枚舉,(由于是凸多邊形,改線段肯定不可能在多邊形內);
3) 相交,將這個交點存入集合S;
將原線段的兩個端點存入集合S,對集合S的點進行x坐標遞增排序(x相同時y坐標遞增排序),然后枚舉相鄰兩個點的中點,判斷是否在在原多邊形內,如果在,那么將這兩個相鄰點練成的線段的長度累加到最后的答案中。如圖1為兩個交點的情況。
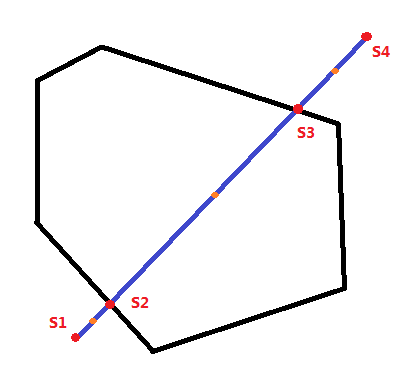
圖1