110 Dungeon 計算幾何:射線和球體相交
111 Very simple problem 二分枚舉
112 a^b-b^a 二分求冪 113 Nearly prime numbers 數論:素數篩選
114 Telecasting station 枚舉115 Calendar 簡單模擬116 Index of super-prime 動態規劃:記憶化搜索117 Counting 二分求冪118 Digital Root 數學題119 Magic Pairs 數論:擴展歐幾里得110 Dungeon 計算幾何:射線和球體相交
題意:給定一條3D射線 和 N個球體�,問射線的各種反彈經過的球體編號�����,如果反射超過10次,只需要輸出前十次���。
題解:很明顯,首先需要枚舉每個球體和當前射線的相交情況�,如果和多個球體相交肯定是取距離最近的球體進行相交計算���,然后計算出空間反射射線���,重復以上操作11次�,如果某次的反射射線已經不能和任何球體相交那么直接跳出這個過程�。
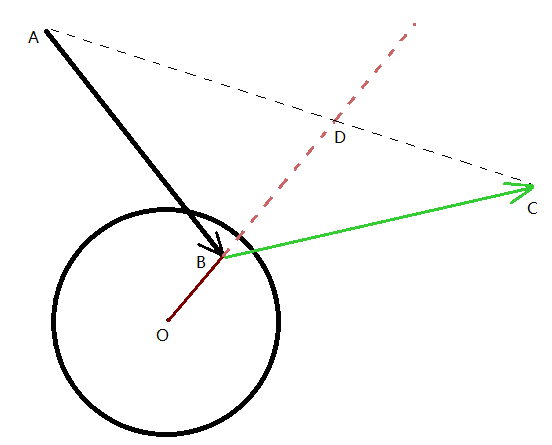
圖1
如圖1,表示射線AB和球O相交于B點���,反射后的射線為BC,BD為球心O到交點的延長線���,那么必定滿足以下幾個條件:
已知A點坐標(xa, ya, za),單位向量tab
B點坐標 為 (xb, yb, zb) = (xa, ya, za) + |AB| * tab (1)
B點在球O上���,所以B點坐標滿足
| (xb, yb, zb) - (xo, yo, zo) | = OB = Ro (2)
將(1)代入(2),可計算出|AB|的長度(由于是射線和球體求交���,這兩個方程求出來的是直線和球體的交點,所以還需要計算方向判斷交點的可行性���,如果交點有兩個,則取距離小的那個���,如果只有一個交點,說明是相切)���,然后利用(1)式計算出B點坐標�����。
2) 射線經過球體的反射射線
假設C點在A經過B點反射后的反射射線上���,并且AB = BC���,那么AC必定和OB延長線相交�,假設交于D點�����;
單位向量cos(ABD) = Iba * Ibd���;
BD = AB * cos(ABD)�;
向量AD = 向量AB + 向量BD�����;
向量AC = 2 * AD�;
點C (xc, yc, zc) = 向量AC + (xa, ya, za);
向量BC求出后返回1) 繼續判斷和別的球的相交情況���;
111 Very simple problem
二分答案 + 大數模擬
題意:給定X( X <= 10100),求X開方后的下取整���。
題解:數組模擬大數。二分答案A�,找滿足 A*A <= X 最大的A即為答案���。
112 a^b-b^a
二分求冪 + 大數模擬
題意:求 ab - ba ( 0 < a, b < 100)。
題解:數組模擬大數。二分求 AB。
當 B == 0 則 AB = 1; 否則 AB = (A2)(B/2) * ( (B mod 2) ? A : 1 ); 遞歸求解。
113 Nearly prime numbers
素數篩選 + 素數判定
題意:判斷一個數是否為兩個素數的積�。
題解:利用傳統的素數篩選將 1-31623 的素數篩選出來�����,31623為平方大于等于109的最小整數,因為一個數的開方內找不到一個(非1或它本身)因子的話它本身就是素數���,所以素數只需要篩選到 109 的開方 即可���。
對于每個數�����,遍歷素數數組���,如果能被某個素數整除,判斷商是不是一個素數�,如果商也是素數結果為Yes���,否則為No�����。
114 Telecasting station
枚舉 + 統計
題意:在X軸上規定一些有權值ai的點 (x1,a1), (x1,a1), (x2,a2) .. (xn,an)要求在x坐標上找到一個點X使得 M = |X-x1|*a1 + ... |X-xn|*an 的值最小�。
題解:細心觀察可以發現���,M是關于X的一次函數�����,所以可以確定X必定為 x1...xn中的某個點。
由于原式中存在絕對值���,為了將絕對值化簡���,可以將X的區間分段,比如當X 為 xj時可以簡化為 M = (X-x1)*a1 + ...(X-xj)*aj + (xj+1-X)*aj+1 + ... + (xn-X)*an
= (X * presum[j] - preproduct[j]) + (postproduct[j+1] - X * postsum[j+1])
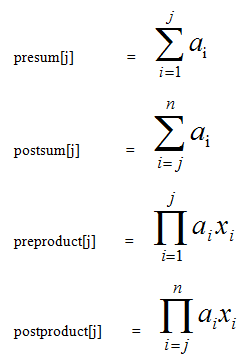
圖2
這些輔助數組可以通過四次線性掃描得出,復雜度O(n)���。然后�,先將xi遞增排序,枚舉每個xi,計算最小值更新M�,就可以在O(n)的時間內求解了。總體算法復雜度為排序復雜度O(n log n)�����。
115 Calendar
簡單模擬
題意:給定一個月份M和天數N�����,求2001的那一天是星期幾。
題解:可以預處理出每個月的天數���,如果天數大于那個月對應的天數或者月數大于12肯定是不可行的�,否則將給定月數M之前的 1到M-1個月的天數相加再加上N得到Sum���,Sum mod 7就可以定位到星期幾了。
116 Index of super-prime
素數篩選 + 記憶化搜索(或 動態規劃)
題意:超級素數是素數下標也是素數的數���,給定一個數N,問這個數能不能被一些超級素數組合出來�,如果可以�,需要滿足超級素數的個數最少,要求輸出一個方案�。
題解:先將滿足條件的 超級素數 篩選出來�����,3 5 11 17等等,然后對于輸入的N進行一次記憶化搜索(DP)
例如 N = 15
那么N的最優值一定是來自 15-3=12���,
15-5=10, 15-11=4 這三個數�����,以此類推�����,遞歸出口是N = 0�,每次計算完N就將它保存下來�,下次就不用重復計算了���。
所以狀態轉移方程為:DP[i] =
min{ DP [ i - p ] , p 為超級素數 } + 1
因為需要輸出組合的序列,所以每次搜索�����,需要保存當前最優值的前驅結點�,最后一次性輸出即可。
117 Counting 二分求余
題意:給定N(N < 10001)個數Ai���,求其中AiM
是K的倍數的數的個數。
題解:對于ab mod c二分求解�����。當
b == 0 則 ab mod c = 1 mod c; 否則 ab mod c = (A2)(B/2)
* ( (B%2) ? A : 1 ) mod c;
118 Digital Root 數學歸納法
題意:定義f(n) 為 n的所有數字的和. 如果 f(n) 是1位數字���,那么它是n的 "digital root"�����,否則n的"digital root" 為 f(n) 的"digital root"�����。
給定數組Ai�,求 A1*A2* … *AN + A1*A2*…*AN-1 + … + A1*A2 + A1 的"digital root"(N <= 1000)���。
題解:定義d(n)為n的"digital root"���,利用數學歸納法可證明(從N=1的情況網上遞推):
1) d( A1*A2* … *AN ) = d( AN * d( A1*A2* … *AN-1 ) )
2) d(A1 + A2 ) = d( d(A1) +d(A2) )
利用這兩點�����,可以直接掃描A數組就可以計算出給定表達式的"digital root"了。
119 Magic Pairs 枚舉 + 擴展歐幾里得
題意:對于所有的(X,Y)在滿足 (A0 * X + B0 * Y) % N = 0 (1) 的情況下,使得(A * X + B * Y) % N = 0 (2) 也成立, 求這樣的 (A, B)���。
題解:首先求出A0、B0�、N三者的GCD�,最后算出來的答案需要乘上這個GCD���。
(A0 * X + B0 * Y) = K * N (3) (K為整數)
(A * X + B * Y) = K' * N (4) (K'為整數)
X = (K*N - B0*Y) / A0
代入(4)式,可得
A*(K*N - B0*Y) + B*A0*Y = K'* N * A0 (5)
化簡得 (6)
(B*A0 - A*B0) * Y = (K'*A0 - K*A) * N (6)
兩邊同時mod N
得 (B*A0 - A*B0) * Y % N = 0 (7)
由于Y為任意整數(即Y有可能和N互素), 所以必須滿足 (B*A0 - A*B0) % N = 0 (8)
可以化簡為 (B*A0 - A*B0) = K'' * N (9) (K''為整數)
A0 * B + N * (-K'') = A*B0 (10)
枚舉A的值�,就可以把方程轉化成了 ax + by = c的形式,其中:
a = A0, b = N, c = A*B0
x = B, y = -K''
利用擴展歐幾里得即可求得最小的滿足條件的x(即B)的值了。
最后的答案需要乘上 A0、B0�����、N 三者的GCD�����。