150 Mr. Beetle II 枚舉
151 Construct a triangle 解析幾何152 Making round 貪心153 Playing With Matches 博弈 + 規律154 Factorial 初等數論
155 Cartesian Tree RMQ
156 Strange Graph 歐拉回路157 Patience 模擬打表150 Mr. Beetle II 枚舉
題意:給定兩個二維坐標上的點(x1, y1)、(x2, y2),坐標范圍為[-106, 106]。求從一個點(x1, y1)到(x2, y2)的直線路徑上經過的第N個方格的左下角坐標,無解輸出no solution。
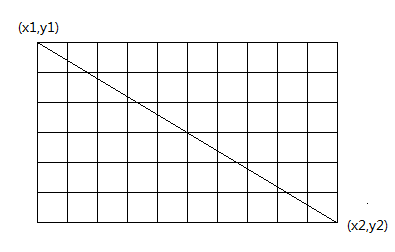
圖1
題解:首先,如果兩個點的x坐標相同或者y坐標相同,則直接無解;否則將(x1, y1)和(x2, y2)一起做相應的平移,使得(x1, y1)和(0, 0)重合,方便計算。
如果x1 < x2,枚舉x坐標屬于(x1, x2],對于每個單位為1的區間[x, x+1]容易計算出y方向上有多少個方格,統計出第n個方格;如果x1 > x2,枚舉x坐標屬于(x2, x1],用同樣的方法進行計算。
151 Construct a triangle
解析幾何
題意:給定三角形的兩條邊AB = c、 AC = b 和 一條中線 AM = m 的長度,求一個滿足條件的三角形的坐標。
題解:由于三角形的坐標可以隨意取,所以為了簡化問題,可以將A點定在坐標原點,B點定在x軸正方向,C則在第一象限或者第二象限;
假設A在原點(0, 0)
B在x+軸上,則有B點坐標(c, 0)
假設C點坐標為(x, y), 中線坐標為 (B + C) / 2,即 ( (x+c)/2, y/2 )
已知AM距離m 和AC距離b,則有:
x2 + y2 = b2 (1)
((x+c)/2)2 + (y/2)2 = m2 (2)
合并(1) (2),則有
-2cx - c2 = b2 - 4 * m2 (3)
x = (4*m2 -b2 - c2)/2/c; (4)
y2 = b2 - x2; (5)
根據(5),可以推出 y2 = b2 - x2 = b2 - ((4*m2 -b2 - c2)/2/c ) 2 =>[ (b+c) 2 - (2m)2 ] * [ - (b-c)2 + (2m)2 ] > 0
b+c > 2m 并且 2m > fabs(b-c)時y才有解,所以當 2*m > (b+c) 或者2*m < fabs(b-c) 為無解的情況。
而我們假設C在第一象限或者第二象限,所以y>0,于是(x, y)可通過(4) (5)求得。
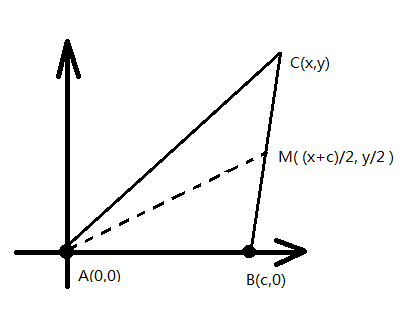
圖2
152 Making round
貪心
題意:給定N(N <= 10000)個數,求每個數在所有數中所占百分比,要求輸出的數之和為100,每個數可以進行上下取整。如:給定三個數3 3 3,那么輸出為 34 33 33。34為向上取整的結果,33為向下取整的結果。
題解:
1)首先求得所有數之和S,將每個數a[i]除上S得到商B[i]和余數M[i]。
2)如果余數為0表示為整除,不能進行上下取整。如果余數不為0,說明它有 +1 或者 +0 的機會。 (因為題目說可以上取整,也可以下取整)
3) 記錄下所有余數不為零的個數T。
4)將所有數的商之和Sum{B[i]} 和 余數不為零的數的個數T 相加,如果小于100,則表明必定無解。否則掃描數組,將 X = 100-Sum{B[i]}-T 的值分派給每個不能整除的數即可(每個數只可分派1)。
153 Playing with matches
博弈
題意:給定N根火柴(N <= 109),每次可以從這些火柴中取1,P1,P2,...,Pm (2<=Pi<=9, 0<=m<=8)根,兩人分別輪次進行拾取,并且總是按照最優策略去取,最后取完火柴的人為輸的人,問當前狀態是否是一個必勝狀態。
題解:經典博弈,對于給定狀態X:
1) 如果按照所有方式取,最后都只能讓對手到達必勝狀態,那么X為必敗狀態;
2) 如果對于某種取法,可以讓對手達到必敗狀態,那么X為必勝狀態;
3) 顯然,0為必勝態,1為必敗態,2為必勝態。
根據以上的性質,可以通過遞推,將火柴根數確定的情況下,將所有狀態算出來,但是由于N <= 109,數據量太大,但是我們注意到每個Pi很小,最大值也只有9,某些大狀態是通過小狀態算出來的,所以必然存在循環。
于是問題就轉化成了求一堆序列的循環節,可以先預處理將5000(足夠大就行)以內的狀態用記憶化搜索算出來,對于每個狀態值,用0表示必勝,1表示必敗。枚舉循環節的長度len,然后檢測是否一個合法的循環節。最后N的狀態值就是N % len的狀態值。
154 Factorial
二分統計 + 初等數論
題意:給定一個數N,求一個最小的數K,使得K!末尾正好有N個0。
題解:因為K!中的質因子中5的個數明顯比2的個數少,所以求末尾有多少個0,其實就是求K!中有多少個質因子5。那么這些質因子一定出現在 5、10、15、25、30、35、... K中,對于 K!,將所有的5的倍數提出來,剩下部分為T,則有:
K! = 1*2*3*4*5*...(K-1)*K = 5 * 10 * 15 * ... * (1*2*3*4*6*7*8*9*11*12*13*14*16*...K) = 5*10*15*...* T = 5* (1*2*3...) * T = 5 * T * K'! , 我們發現5*T中5的質因子個數為T個,K'! 中的5的個數則可以轉化成子問題求解,這樣就變成了一個遞歸求解K中質因子為5的個數S的問題,遞歸方程為 S[ K ] = K/5 + S[K/5] ( K > 0 ) 當K = 0時返回0,即遞歸出口。
那么就可以二分枚舉一個K,然后通過上面的遞歸求解K中5這個質因子的個數,然后和N比較,如果找不到一個K,使得它的5質因子的個數為N則無解,否則找一個最小的。
155 Cartesian Tree
RMQ(or ZigZag)
題意:給定N(N <= 50000)個整數對(key, a),要求將他們組織成一棵樹二叉樹,并且對于樹的任意一個結點,滿足如下兩個性質:
1) 當前結點的a值大于它父節點的a值(小頂堆的性質);
2) 當前結點的key值大于左子樹的key值,并且小于右子樹的key值(排序二叉樹的性質);
題目保證所有的key值和a值都不同。
題解:首先將所有整數對按key值遞增排序,這樣我們只需要對數組進行切分,如果第t個結點作為根結點,那么[1, t-1]必定是它的左子樹集合,[t+1, N]必定是它的右子樹集合,這樣就能夠保證第二個條件,而第一個條件需要滿足父節點的a值小于左右子樹的a值,所以第t個結點必定是所有數中a值最小的,于是可以規約出一個遞歸算法,對于當前區間[l, r],找到區間內a值最小的作為根結點,然后將它左邊的區間和右邊的區間進行相同的遞歸運算。初始區間為[1, N],當[l, r]滿足 l > r即為遞歸出口。求區間最小值可以采用RMQ。總的時間復雜度為排序的時間復雜度O(N log N)。
RMQ 資料參閱 http://www.shnenglu.com/menjitianya/archive/2014/06/26/207420.html
156 Strange Graph
歐拉回路
題意:給定一個N(N <= 10000)個點的連通圖,這個圖滿足以下性質:
1) 每個頂點v的度數都大于等于2;
2) 如果頂點v的度數等于2,那么它連接的兩個頂點不相鄰;
3) 如果頂點v的度數大于2,那么和v相鄰的點u滿足以下條件之一;
a) u的度數等于2;
b) 任何和v相鄰的點(除了u)中都兩兩相鄰;
求這個圖的一個哈密爾頓回路(經過每個頂點一次的回路)。
題解:首先將所有度數為2的點進行標記,那么從這個圖的定義中可知,未標記的點必定是在一個完全子圖中的,將圖中所有完全子圖中的點縮成一個點,對縮完點的圖統計度數,如果所有的點的度數都為偶數,那么必定存在一個歐拉回路,求出歐拉回路后再拆點轉換成哈密爾頓回路;否則,歐拉回路不存在,哈密爾頓回路也就不存在。
157 Patience
打表題
題意:給定N(1 <= N <= 13),表示(1 2 3 ... N 空)這N+1個位置,其中N個位置隨機排放著1-N中的某一張牌,每次可以在“空”左邊的位置找到一張牌K,然后將K+1這張牌放在“空”的位置上,問哪些初始狀態可以到達一個狀態使得前N個格子的牌有序排列(第N+1個位置留空)。
題解:從(1 2 3 ... N 空)這個狀態起,反向模擬,能夠到達的狀態都是可達狀態,統計所有可達狀態的個數,N的最大值為13,時間上不允許可以客戶端計算出值然后打表!
158 Commuter Train
二分枚舉
題意:車站長度為L(L <= 5000),給定N(N<= 300)個乘客在車站的位置,以及一輛公交車的M(M <= 300)個車門離車頭的位置,乘客一定會選擇離自己最近的車門進入,問這輛車要停在哪里可以使得所有人進入車門需要走的距離總和最大,好變態的想法。
題解:只要枚舉車需要停靠的位置,然后枚舉每個人到達的那個車門花費的距離總和,取最大值就是答案。
這里對于某個人需要去哪個車門可以采用二分枚舉,因為車門是有序的,只要二分找到離它最近的左車門,那么下一個就是最近的右車門(需要考慮邊界,最左和最右的情況都只有一個車門),然后取左、右車門的距離小者。仔細想一下,最大值不一定出現在整點上,也有可能出現在0.5的位置上,所以可以將所有坐標都乘2,然后最后答案再除二避免精度誤差。
159 Self-Replicating Numbers
深度優先搜索
題意:求N(N <= 2000)位B進制數中平方的最后幾位等于該數本身的數的個數。
題解:利用dfs從最后面一位digit開始枚舉[0, B),模擬相乘后對應位的余數,如果和該數的枚舉那一位不相符則不進行下一步搜索,當枚舉到第N位完畢,則將解保存,這里需要注意當N為1的時候,最高位可以為0,否則最高位為0的情況需要去掉(最高位為0說明它不是N位數(N>1))。