PKU 1961 http://poj.org/problem?id=1961
题意�Q�给定一个长度�ؓN(N <= 106)的字�W�串S�Q�求它的所有前�~�中能够表�C�成AK的前�~��Q��ƈ且要求求出每个前�~�对应�?/span>K�?/span>
题解�Q?/span>KMP
利用KMP求出该串�?/span>Next数组�Q�然后枚举每个前�~��Q�根�?/span>Next数组的定义,对于某个前缀S[1...i]�Q�有S[1...Next[i]] = S[i-Next[i]+1...i]�Q�假讑։��~�S[1...i]能够表示�?/span>AK的�Ş式,�?/span>A = S[Next[i]+1...i]�Q�所以必���L����?/span>i能够�?/span>i - Next[i] 整除�Q�满���x��件后K = i/( i - Next[i])�?/span>
B. Corporative Network
PKU 1962 http://poj.org/problem?id=1962
题意�Q�给�?/span>N(N <= 20000)个点�?/span>M(M <= 200000)�ơ操作,每次操作有两�U�类型:
I a b ��?/span>a的父�l�点设�ؓb�Q��ƈ且合�q�距���Mؓ |a-b| mod 1000
E a 询问a到根�l�点的合�q�距���R�?/span>
题解�Q��ƈ查集
利用路径压羃的思想�Q�用dist[p]表示p�?/span>p的父�l�点的合�q�距���,每次查询的时候篏�?/span>p到根�l�点的合�q�距���,�q�且��?/span>p�?/span>p所在树的根�l�点R的�\径上的所有点的父�l�点都设�?/span>R�Q�然后更新各自的合�ƈ距离�?/span>
合�ƈ操作O(1)�Q�查询操作��d��杂度O(N)�?/span>
C. Cave Exploration
PKU 1963 http://poj.org/problem?id=1963
题意�Q�给�?/span>N(N <= 1000)条水�q�x��者垂直的走廊�Q�再�l�定走廊上�Q意一个坐标点作�ؓ��L��以及方向�Q�按照以下策略走�Q�能够左转就左�{�Q�不能则�W�直赎ͼ�不能�W�直走就双��{�Q�都不能���掉头。这栯���最后绕一圈又会回到�v点,问哪些走廊是没有�l�过的,只要有一个点走过���q���l�过�?br /> 题解�Q�模�?/span> + 哈希�?/span>
���水�q�线�D�和竖直�U�段分开存,分两�U�情况讨论:
1、水�q�线�D?/span>
对于��L��一�Ҏ���q�线�D�,枚�D所有的竖直�U�段�Q�计���出交点和水�q�线�D늚�端点�Q�保存下来�ƈ且按x坐标递增排序�Q�去掉重复点�Q�利用双向链表将两个盔R��点连接�v来,�׃��x�?/span>y坐标范围�?/span>-32767~32767�Q�而交�Ҏ��不会���过N2�Q�所以可以采用哈希将二维的点映射��C��位数�l�中。每个点记录水��^走廊的编受��?/span>
2、竖直线�D?/span>
同上操作�Q�不同的是每个点记录竖直走廊的编受��?/span>
�l�过1�?/span>2两步操作后,走廊上的关键点已�l�被���L��化了�Q��ƈ且所有点都通过四向链表串接��h���Q�然后只需要从��L��开始模拟行走即可,走到一个关键点�Q�将关键�Ҏ��在的两个走廊�~�号标记掉,最后统计没有标记的走廊�~�号���是�{�案了�?/span>
D. City Game
PKU 1964 http://poj.org/problem?id=1964
题意�Q�给定一�?/span>M*N(M <= 1000�Q?/span>N <= 1000)�?/span>01矩阵�Q�求它的一个子矩阵�Q�满���矩阵元素全�?/span>1�Q��ƈ且面�U�最大�?/span>
题解�Q�枚举行�Q�对于第i行,以第i行�ؓ��L���Q�扫描每一�?/span>j�Q�找到第一个不�?/span>1的数所在的位置P[j]�Q���oK[j] = P[j] - i�Q�于是问题�{化成了一个一�l�的问题�?/span>
L[i] 表示 K [ L[i]+1 ... i] 中的元素都大于等�?/span>K[i]�Q�但�?/span>L[i]���于K[i]�Q?/span>
R[i] 表示 K [i ... R[i]-1] 中的元素都大于等�?/span>K[i],但是R[i]���于K[i]�Q?/span>
Max{ (R[i] - L[i] - 1) * K[i], 1 <= i <= N }���是以当前枚举行����v点的最大矩阵,枚�DM�ơ取最大值就是全局的最大子矩阵了�?/span>
E. Cube Root
PKU 1965 http://poj.org/problem?id=1965
题意�Q�给定一个不���过150个数字的正整敎ͼ�求它的三�ơ方根,�_����到小数点�?/span>10位�?/span>
题解�Q�大数模�?/span>
���输入的�?/span>X用字�W�串存储�Q�乘�?/span>1030�Q�利用二分求出最大的Y�Q����?/span>Y3 <= X。然后在Y的后十位前插入一个小数点�Q�输出即可�?/span>
F. Cable TV Network
PKU 1966 http://poj.org/problem?id=1966
题意�Q�求囄���点连通度。给定一�?/span>N(N <= 50)个点的图�Q�求��L��臛_��多少个点能够���它变成一个非�q�通图�?/span>
题解�Q�搜�?/span> + 剪枝 (或�?/span> 最大流)
枚�D每个点去掉或不去掉,��d��250�U�状态,每次��L��点后判断当前囄����q�通性,一旦破坏了�q�通,��L��的点数即为答案;如果发现某个点去掉后�Q�剩下点�l�成的图变成了一个完全图�Q�那么不用���l�搜索了�Q�因为当前状态下不可能将剩下的图变成非连通图了;如果��L��的点数超�q�目前的最优解也直接剪枝�?/span>
好吧...一定是数据�׃��-_-||�Q�正解是最大流拆点�?/span>
G. Alibaba
PKU 1967 http://poj.org/problem?id=1967
题意�Q�给�?/span>N(N <= 104)个整数对(Pi, Di)表示�?/span>Pi位置有一个宝物,�q�且需要在Di 旉���之前取走(�l�出��序�?/span>Pi递增的顺�?/span>)。�v始可以�Q意选择一个位�|�,往左或者往叛_��宝物�Q�问是否能够保证每个物品都在Di旉���之前取走(旉���和距���d���p�Mؓ1:1)�Q�如果可以,�l�出取完所有宝物的最���时间�?/span>
题解�Q�搜�?/span> + 剪枝
首先可以惛_��的是�Q��v始位�|�一定是N个宝物所在位�|�中的其中一个,所以首先可以枚举每个宝物的起始点,比如当前位置�?/span>pos�Q�那么在�W?/span>0�U�内�Q�访问过的区间�ؓ[pos, pos]�Q�可以选择往左走�Q�也可以选择往双����Q�那么是不是只要选择某个方向走完�Q�然后再反方向走到底如果能够满��所有点都在截止旉���内完成一定是对的呢?�{�案是否定的�Q�来看一�l�数据,如图1�Q��v始点只能选择3号位�|�,�q�且只能选择往双����Q�走�?/span>4后再折回走到2�Q�然后再折回走到5�Q�以此类推,�q�且只有�q�一�U��\径才能满���x��有宝物都在截��x��间内取完�?/span>
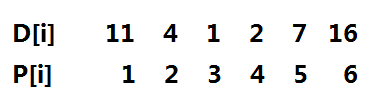
�?/span>1
按照�q�个思�\�Q�进行状态的划分�Q�假讑ֽ�前已�l�访问的区间�?/span>[L, R]�Q��ƈ且现在的位置处于pos位置(�q�里pos要么�{�于L�Q�要么等�?/span>R)�Q�所以可以用三维来表�C�状�?/span>DP[s][l][r](l�?/span>r表示讉K���q�的区间的左右端点,如果当前位置�?/span>l�?/span>s = 0�Q�如果当前位�|�在r�Q�则s=1)�Q���d��状态数�?/span>N2�Q�状态�{�Uȝ��时候由大状态推���状态,�?/span>DP[s][l][r]一定是�?/span>DP[0][l-1][r]�?/span>DP[0][l][r+1]�?/span>DP[1][l-1][r]�?/span>DP[1][l][r+1]�q�四个状态得出�?/span>
考虑�?/span>N比较大,所以把所有状态存储到数组中再利用动态规划进行递推�Q�如果数据量不多的话�Q�可以卡�q�,但是状态存储需要用滚动数组�Q�否则内存吃不消�Q�也可以采用搜烦 + 剪枝�Q�思�\是沿用了动态规划的思想�Q�假讑ֽ�前已�l�访问的区间�?/span>[L, R]�Q�现在的位置处于pos位置(�q�里pos要么�{�于L�Q�要么等�?/span>R)�Q��ƈ且已�l���用了T的时��_��无论当前�?/span>pos是在左区间端�?/span>L上还是在叛_��间端�?/span>R上,他都可以选择走到L-1(L > 1)�Q�或�?/span>R+1(R < N)�Q�于是就可以递归求解了,递归出口�?/span>L=1�Q?/span>R=N的时候�?/span>
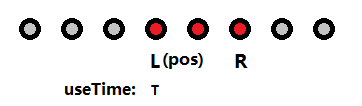
�?/span>2
如图�Q�已�l�访问的宝物为红色标记的点,灰色标记的�ؓ未曾讉K���q�的�Q��ƈ且现在的位置在已�l�访问区间的左端�?/span>L上,已经使用�?/span>T的时��_��我们需要判断这个状态是否合法,则需要满���以下的几个不等式�?/span>
1、保证右�Ҏ��讉K��的都能在截止旉���内访问到�Q?/span>
T + (P[R] - P[L]) + (P[R+1] - P[R]) < D[R+1]
T + (P[R] - P[L]) + (P[R+2] - P[R]) < D[R+2]
...
T + (P[R] - P[L]) + (P[N] - P[R]) < D[N]
���这些等式化����Q�可得:
T - P[L] < D[R+1] - P[R+1]
T - P[L] < D[R+2] - P[R+2]
...
T - P[L] < D[N] - P[N]
再进行进一步化����Q�得�Q?/span>
T - P[L] < Min{ D[k] - P[k], R < k <= N }
2、保证左�Ҏ��讉K��的都能在截止旉���内访问到�Q?/span>
同理�Q�可以得出:
T + P[R] < Min{ D[k] + P[k], 1 <= k < R }
那么�Q���o POSTM[i] = Min{ D[k] - P[k], i < k <= N }
PREM[i] = Min{ D[k] + P[k], 1 <= k < i }
�q�两个数�l�可以分别通过一�ơ逆序和顺序的�U�性扫描求出来�Q�用于搜索的时候判断可行性。例如,�?/span>T - P[L] >= POSTM[R] 表示在右�Ҏ��讉K��的宝物中有至���一个宝物不能在截止旉���前被讉K��刎ͼ�T + P[R] >= PREM [R]表示在左�Ҏ��讉K��的宝物中有至���一个宝物不能在截止旉���前被讉K��刎ͼ�直接剪枝�?/span>
�q�需要一个剪枝,���是在当前时�?/span>T加上当前状态下预计讉K��完所有宝物的最���时�?/span>已经比之前求出的最���时间大�Q�直接剪枝�?/span>
H . Booklets
PKU 1968 http://poj.org/problem?id=1968
题意�Q?/span>N(N <= 3000)本小册子需要分配给S个学校,每个学校得到的是N/S的上整本册子或�?/span>N/S的下整本册子�Q�每本册子有一个页敎ͼ��q�且规定分配册子的时候按照页数递增来分配,先把上整本册子分完再分下整的�Q�对于每个学校的分书规则�Q�按照输入的��序�q�行分配。求问第T个学校分到的�W�一本册子的��|���?/span>
题解�Q�需要求出几个量�Q?/span>
上整册子的数�?/span>UIP = (N+S-1) / S;
下整册子的数�?/span>LIP = N/S;
分到上整册子数目的学校个�?/span>UIPC = N % S;
分到下整册子数目的学校个�?/span>LIPC = N - N % S;
首先�Ҏ��有的册子按页数递增来排�?/span>(如果��|��相同按照下标递增排序)�Q�然后减��d��T-1个学校的册子��L���Q�容易得出第T个学校分到的册子数目C�Q�从接下来的C个册子中扑ֈ�之前下标最���的册子�Q�它对应的页数就是答案�?/span>
I. Count on Canton
PKU 1969 http://poj.org/problem?id=1969
题意�Q�给定下图所�C�的无限分数序列�Q��ƈ且按照蛇形方式编��P��即第一个�ؓ1/1�Q�第二个�?/span>1/2�Q�第三个�?/span>2/1�Q�第四个�?/span>3/1�Q�以此类推,问第N个分数是什么�?/span>
1/1 1/2 1/3 1/4 1/5 ... 2/1 2/2 2/3 2/4 3/1 3/2 3/3 4/1 4/2 5/1题解�Q�数学题�?/span>
首先二分求出在第几条斜线上,�?/span>(K-1)K/2 < N的最大的K�Q�然后求�Ҏ��K的奇偶性求�����形在�W?/span>K条斜�U�的行走方向�Q�第N - (K-1)K/2 个数���是�{�案�?/span>
]]>

A . The Hardest Problem Ever
PKU 1298 http://poj.org/problem?id=1298
题意�Q�解码题�Q�按照如下对应关�p�解码:
密文 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
原文 V W X Y Z A B C D E F G H I J K L M N O P Q R S T U
题解�Q�简单题�?/span>
B. Polar Explorer
PKU 1299 http://poj.org/problem?id=1299
题意�Q�给定圆的半�?/span>X�Q�求圆周上两个点A�?/span>B的距���,其中圆心�?/span>AOB的角度�ؓZ(0 <= Z <= 360)�?/span>
题解�Q�核心是Z如果大于180�Q�则Z = 360 - Z�Q�即走劣弧。而且题目求的是来回一�ơ,所以计���的时候弧长要�?/span>2�?/span>
C. Door Man
PKU 1300 http://poj.org/problem?id=1300
题意�Q�给定一些边和�v�?/span>s�Q�求能否扑ֈ�一条从s�?/span>0的通�\�Q��ƈ且要求访问所有的辏V�?/span>
题解�Q�欧拉回路可行解判定�?/span>
首先利用flood fill�?/span>s遍历全图�Q�如�?/span>0�Ҏ��有被讉K��到则必定不存在;然后判断度数不�ؓ0的点是否有未被访问到的,如果有,说明图不�q�通,也必定不存在解;最后统计度��Cؓ奇数的点的个�?/span>P�Q�以及具体的点:
1) P = 0�Q�则必定有解�Q?/span>
2) P > 2�Q�则无解�Q?/span>
3) P =2, 那么有解的前提是两个奇度数点中一个是s�Q�另一个是0�Q�否则无解�?/span>
D . The Umbrella Problem 2054
PKU 1301 http://poj.org/problem?id=1301
题意�Q�给定一�?/span>10X10的地图,玩家从第一行的某一个点出发�Q�每一步行�~�号+1�Q�列�~�号增量有三�U�选择(-1, 0, 1)�Q�图中标��CؓS(laser gun)的点不能赎ͼ��q�且S的点会发出镭���光�Q�第0�U�朝上发���,�W?/span>1�U�朝叻I���W?/span>2�U�朝下,�W?/span>3�U�朝左,循环往复,发射长度一直到地图边缘。问能否走到最后一行标��CؓG(grass)的地斏V�?/span>
题解�Q�广搜�?/span>
hash[4][R][C]表示状态,每走一步,利用步数 mod 4计算出镭���光的方向,然后���所有的镭射光可辑�域全部标记出来,未标记的点�ؓ可达点,枚�D三个方向�q�行搜烦�?br />
E. Blue Gene, Jr.
PKU 1302 http://poj.org/problem?id=1302
题意�Q�一个长度�ؓN(N <= 20)的病毒基因串A[1...N]�q�行变异�Q�变异过�E�从左往叻I��分情况讨论:
1) 如果�W?/span>i个字�W�是 A-Z�Q�则它将变异成数�?/span>n mod 10�Q?/span>n表示A[i+1...N]中变异基因的数目�Q?/span>
2) 如果�W?/span>i个字�W�是 1-9�Q�则它变异成A[i] - 1�Q��ƈ且如果第p (p = i + A[i])个基因存在的话,从第p个基因开始变异;否则从第i+1个基因开始变异;
题解�Q�题意理解后���是个水题了�Q�递归求解�?/span>
F . Byte Me!
PKU 1303 http://poj.org/problem?id=1303
题意�Q�二�q�制二十一�?/span>(二进刉���杰克)是由两种牌组成的游戏�Q�一�U�称�?/span>bytes(一�?/span>8比特的序列表�C?/span>0-255之间的数)�Q�一�U�称�?/span>nibbles((一�?/span>4比特的序列表�C?/span>0-15之间的数)�Q�游戏玩法如下:
1) 游戏的目标是获得���量接近510分,�q�且不能���过它;
2) 每个玩家有两张牌�Q�一张面朝上�Q�一张面朝下(庄家不知道是什么牌)�Q?/span>
3) 每个玩家有四�ơ叫牌机会,可以�?/span>bytes�Q�也可以�?/span>nibbles�Q�但是如果分数超�q?/span>510则不能再叫牌�Q?/span>
4) 所有的叫牌都是面朝上的�Q?/span>
5) 如果玩家分数���过510�Q�立卛_��������Q?/span>
5) 庄家最后一个叫牌;
7) �q�_��的情况庄家胜(如果所有�h都超�q?/span>510分,庄家�q�是赢的)�Q?/span>
庄家的规�?/span>如下�Q?/span>
1) 当看到自己和其他人面朝上的牌�Q�判断已�l�必胜时不要再叫牌了�Q?/span>
2) 如果��d�����于382�?/span> 需要叫一��?/span>byte牌;
3) 如果��d�����于�{�于500�?/span> 需要叫一��?/span>nibble牌;
�q�有两个隐藏规则�Q?/span>
1) 你是庄家�Q?/span>
2) 每个非庄家的玩家面朝下的牌是11111111�Q�但是庄家不知道�Q�,面朝上的牌给定;
3) 非庄家不会叫�?/span>(因�ؓ他们比较�W?/span>)�Q?/span>
�l�定庄家的牌和其他玩安���朝上的牌�Q�以及牌堆中�?/span>bytes牌和nibble牌,求庄家的四次叫牌能否莯����Q?/span>
题解�Q�题目说了一大堆�Q�最后非庄家的玩安���不会叫牌�Q?/span>o(╯□╰)o...所以只要根据庄家的规则�q�行叫牌�Q�然后判断是否能够胜出即可;
因�ؓ其他人都不叫牌,每个人都有两张牌�Q�所以其他�h的��d��不可能超�q?/span>510分,所以,如果庄家叫牌���过510分直接被判�ؓ负�?/span>
每次叫牌前先判断所有玩家的朝上的卡片分数加�?/span>255和庄家当前得分进行比较,如果有一个玩家分数大于庄家分敎ͼ�则庄家按�?/span>382�?/span>500�q�两个区间进行叫牌�?/span>
四次叫牌�l�束�Q�如果所有玩家分数都���于�{�于庄家分数�Q�则判断庄家分数是否大于510�Q�如果是�Q�输�?/span>Bust!�Q�否则输�?/span>Win!�Q�如果小于某个玩家的分数�Q�那么输�?/span>Lose!�?/span>
G . World's Worst Bus Schedule
PKU 1304 http://poj.org/problem?id=1304
题意�Q�公交�R站有N(N <= 20)辆�R�Q�每辆�R的发车时间间隔�ؓa1 a2 a3 a4... a1 a2 a3 a4... a1 a2 a3 a4...�Q���@环发车,问某人在T时刻赶到公交车站�Q�最���需要等待多���时间能够乘上公交�R�?/span>
题解�Q�对于每辆公交�R�Q�设它的所有时间间隔之和�ؓS�Q���oT' = T mod S�Q�然后枚举所有的发�R间隔�Q�前i个发车间�?/span>a[i]之和减去T'中的最���正值就是等�q�辆公交车需要的旉����Q�取所有公交�R的最���时间就是所求�?/span>
]]>
A. Artificial Intelligence?
PKU 2256 http://poj.org/problem?id=2256
题意�Q�功率的计算公式为P = UI�Q�给定一句话�Q�这句话中一定会包含三个变量中的两个�Q�求另外一个,�q�且单位会有三种前缀m(�?�Q�k(�?�Q�M(�?�?/span>
题解�Q�字�W�串扫描�?/span>
gets��d��字符�Ԍ���q�行一�ơ遍历,查找是否包含子串’P=’, ‘U=’, ‘I=’, 格式化它后面的数字,需要用double来存�Q�然后检查单位前�~��Q�m需要将原值除�?03�Q�k需要将原��g���?03�Q�M需要将原值常�?06。然后分三种情况计算未知的那个值即可�?/span>
B. Balancing Bank Accounts
PKU 2257 http://poj.org/problem?id=2257
题意�Q�给定N(N <= 20)个�h�Q�以及M(M <= 1000)条关�p�,每条关系的描�q�CؓnameA nameB C�Q�表�C�nameA�q�个人给了nameB�q�个人C块钱�Q��ؓ了让所有�h都不亏,需要再�l�出臛_��N-1条关�p�,使得所有�h都收支��^衡�?/span>
题解�Q�贪心�?/span>
首先���所有�h分成两堆�Q�from_set表示收入大于支出的�h的集合,to_set表示支出大于收入的�h的集合,�q�且记录他们各自�?nbsp;|收入-支出|�Q�然后对于所有的from_set的�h�?nbsp;|收入-支出| �q�行递增排序�Q�枚举每个from_set中的人f�Q�去to_set中找��C��个�ht�Q�满���f剩余的钱���于�{�于t亏损的钱�Q��ƈ且t是to_set中亏损最���的人,如果找不到这��L��人,那么扑ֈ�亏损最多的那个人,���f的钱�l�t�Q���@环往复,直到f的钱�l�完为止�?/span>
当from_set中的所有�h���钱全部�l�了to_set中的人后�Q�to_set中也���没有�h亏损了,所有�h辑ֈ�收支�q�����?/span>
C. The Settlers of Catan
PKU 2258 http://poj.org/problem?id=2258
题意�Q�给定一个N(N <= 25)个点�Q�M(M <= 25)条边的图�Q�求囄���最长�\�Q�点允许重复�Q�边不允讔R��复�?/span>
题解�Q�前向星 + dfs�?/span>
利用前向星存双向边,以每个点����v�Ҏ��搜遍历整个图�Q�访问过的边哈希�Q�搜索过�E�更新最长�\卛_���?/span>
D. Team Queue
PKU 2259 http://poj.org/problem?id=2259
题意�Q�Team Queue是这样一�U�queue�Q�每个元素都有一个Team�?/span>
对于queue的push操作�Q�被push的元素从queue中从头到���扫描,如果扫到一个元素和它属于同一个Team�Q�那么直接将它插入到�q�个元素后面�Q�如果没有扫刎ͼ�直接插到对列����?/span>
对于queue的pop操作�Q�等同于普通queue的pop操作�?/span>
队伍数N���于�{�于1000�?/span>
题解�Q�模拟,开1000个队列�?/span>
对于插入操作�Q�每个Team的元素插入到对应的队列中�Q��ƈ且记录当前Team的最早插入时间。O(1)
对于弹出操作�Q�枚举所有Team的队列首元素�Q�从中找旉���最早的�Q�然后对那个队列执行弹出操作。O(N)�?/span>
E. Error Correction
PKU 2260 http://poj.org/problem?id=2260
题意�Q�给定N*N(N < 100)�?1矩阵�Q�问是否所�?nbsp;行和 �?nbsp;列和 都是偶数�Q�如果是输出OK�Q�如果不是,是否能够通过改变一个��g���?nbsp;都是偶数�Q?nbsp;都不行输出Corrupt�?/span>
题解�Q�扫描�?/span>
扫描所�?nbsp;行和 �?nbsp;列和�Q�如果正好有其中一行R是奇敎ͼ��q�且其中一列C是奇敎ͼ�那么改变(R, C)的值就能保证全是偶敎ͼ�否则要么是OK�Q�要么是Corrupt�?/span>
F. France '98
PKU 2261 http://poj.org/problem?id=2261
题意�Q�给�?6个国家进行淘汰赛�Q�以及一�?6*16的矩阵A�Q�其中A[i][j]表示i号国家打败j号国家的概率�Q�问每个国家取得冠军的概率�?/span>
题解�Q�动态规划�?/span>
dp[0][i] 表示 1/2册��� �W�i个�h莯���的概�?/span>
dp[1][i] 表示 1/4册��� �W�i个�h莯���的概�?/span>
dp[2][i] 表示 1/8册��� �W�i个�h莯���的概�?/span>
dp[3][i] 表示 ��d���?nbsp;�W�i个�h莯���的概�?nbsp;
1) 那么昄���dp[0][i] = A[i][i^1]
2) dp[1][i]的概率取决于1/2册���时第i个�h莯���的概率乘上他打��|1/4册���中同�l�的那两个�h的概率;
3) dp[2][i]的概率取决于1/4册���时第i个�h莯���的概率乘上他打��|1/8册���中同�l�的那四个�h的概率;
4) dp[3][i]的概率取决于1/8册���时第i个�h莯���的概率乘上他打��| ��d��赛中同组的那八个人的概率�Q?/span>
直接递推求解�Q�dp[3][i]���是所求�?/span>
G. Goldbach's Conjecture
PKU 2262 http://poj.org/problem?id=2262
题意�Q�将一个数分解成两个奇素数的和�?/span>
题解�Q�素数筛选,枚�D�?/span>
H. Heavy Cargo
PKU 2263 http://poj.org/problem?id=2263
题意�Q�给定一个有向图�Q�边权W(u, v)表示从u到v的最大蝲重�ؓW(u, v)�Q�在�l�定s和t�Q�求s到t 的最大可能蝲重�?/span>
题解�Q�二分答�?nbsp;+ 判断�q�通性�?/span>
二分枚�D�{�案T�Q�然后从��L��到终点进行连通性判定,如果�Ҏ�����于T的边不可达,二分的最大值就是答案�?/span>
]]>
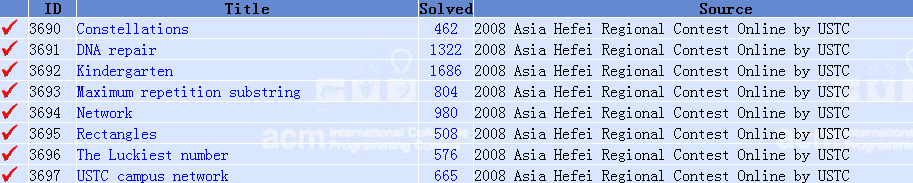
A. Constellations
PKU 3690 http://poj.org/problem?id=3690
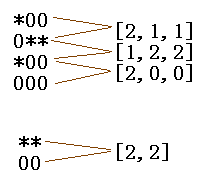
题意�Q�给�?/span>N*M(N<=1000, M <= 1000)�?/span>01矩阵S�Q�再�l�定T(T <= 100)�?/span>P*Q(P <= 50, Q <= 50)�?/span>01矩阵�Q�问P*Q的矩阵中有多���个�?/span>S的子矩阵�?/span>
题解�Q�位压羃 + KMP
�׃��P <= 50�Q�所以我们可以把所�?/span>P*Q的矩阵进行二�q�制位压�~�,��?/span>P*Q的矩�늚�每一列压�~�成一�?/span>64位整敎ͼ��q�样P*Q的矩阵就变成了一个长度�ؓQ的整数序列,用同��L��方式�?/span>N*M的矩阵进行压�~�,��d��可以产生(N-P+1)个长度�ؓM的整数序列,剩下的就是进行最�?/span>(N-P+1)��?/span>KMP匚w��了�?/span>
KMP相关���法可以参阅�Q?/span>
http://www.shnenglu.com/menjitianya/archive/2014/06/20/207354.html
�?/span>1 ‘*’代表二进制的1, ’0’代表二进制的0
B. DNA repair
PKU 3691 http://poj.org/problem?id=3691
题意�Q�给�?/span>N(N <= 50)个长度不���过20的模式串�Q�再�l�定一个长度�ؓM(M <= 1000)的目标串S�Q�求在目标串S上最���改变多���字�W�,可以使得它不包含��M��的模式串�Q�所有串只有ACGT四种字符�Q��?/span>
题解�Q?/span>AC自动�?/span> + 动态规�?/span>
利用模式串徏�?/span>trie图,trie囄���每个�l�点(即下文讲到的状�?/span>j)�l�护三个�l�构�Q?/span>
Node{
Node *next[4]; // 能够到达的四个状�?/span> 的结�Ҏ���?/span>
int id; // 状�?/span>ID�Q�用于到数组下标的映��?/span>
int val; // 当前状态是否是一个非法状�?/span> �Q�以某些模式串结���)
}
�?/span>DP[i][j]表示长度�?/span>i (i <= 1000)�Q�状态�ؓj(j <= 50*20 + 1)的字�W�串变成目标�?/span>S需要改变的最���字�W�,讑ֈ�始状�?/span>j = 0�Q�那�?/span>DP[0][0] = 0�Q�其他均为无�I�大。从长度i�?/span>i+1�q�行状态�{�U�,每次转移枚�D共四个字�W?/span>(A�?/span>C�?/span>G�?/span>T)�Q�如果枚丑ֈ�的字�W�和S对应位置相同则改变�?/span>T=1�Q�否�?/span>T=0�Q�那么有状态�{�U�L���E?/span> DP[i][j] = Min{ DP[i-1][ fromstate ] + T, fromstate为所有能够到�?/span>j的状�?/span> };最�?/span>DP[n][j]中的最���值就是答案�?/span>
C. Kindergarten
PKU 3692 http://poj.org/problem?id=3692
题意�Q�给�?/span>G(G <= 200)个女孩和B(B <= 200)个男孩,以及M(0 <= M <= G*B)条记�?/span>(x, y)表示x号女孩和y��L��孩互相认识。�ƈ且所有的奛_��互相认识�Q�所有的男孩互相认识�Q�求扑ֈ�最大的一个集合��得所有�h都认识�?/span>
题解�Q�二分图最大匹�?/span>
一个点集中所有�h都认识表�C����个点集是个完全图�Q�该问题���是求原囄���一个最大团(最大完全子�?/span>)�Q�可以�{化�ؓ求补囄���最大独立集�Q�而补图恰好是个二分图。二分图的最大独立集 = �ȝ���?/span> - 二分囄���最大匹配。于是问题就转化成了求补囄���最大匹配了�?/span>
D. Maximum repetition substring
PKU 3693 http://poj.org/problem?id=3693
题意�Q�给定长度�ؓN(N <= 105)的字�W�串S�Q�求它的一个最多重复子�?/span>(注意�Q�最多重复子串不�{�于最镉K��复子�Ԍ���?/span>ababab�?/span>aaaa应该取后�?/span>)�?/span>
题解�Q�后�~�数组 + RMQ
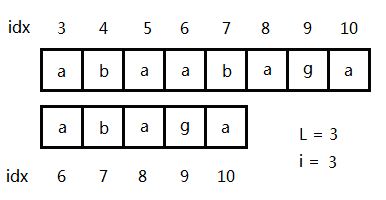
枚�D重复子串的长�?/span>L�Q�如果对于某�?/span>i�Q�有S[i*L ... N]�?/span>S[(i+1)*L ... N]的最长公共前�~�大于�{�于L(�q�一步可以利用后�~�数组求解height数组�Q�然后通过RMQ查询区间最���值来完成)�Q�那么以i*L为首�Q�长度�ؓL的子串至���会重复两次�?/span>
�?/span>2
如图�Q?/span>L=3�Q?/span>i=3的情况,S[3...10]�?/span>S[6...10]的最长公共前�~��?/span>3�Q�即S[3...5]�?/span>S[6...8]完全匚w���Q�所�?/span>S[3...5]重复了两�ơ。反之,如果最长公共前�~����于L�Q�必定不会重复(因�ؓ两个子串之间出现了断层)�?/span>
推广到更一般的情况�Q�如�?/span>S[i*L ... N]�?/span>S[(i+1)*L ... N]的最长公共前�~��?/span>T�Q�那么以S[i*L]为首的重复子串的重复�ơ数�?/span>T / L + 1�Q�而且我们可以发现如果�?/span>S[i*L]为首�Q�长度�ؓL的子串的重复�ơ数大于�{�于2�Q�那么它一定不会比�?/span>S[(i+1)*L]为首的子串的重复�ơ数���,�q�个是显然的�Q�比�?/span>L�?/span>2的时候,ababab一定比abab多重复一�ơ,��Z���q�个性质�Q�我们定义一�?/span>new_flag标记�Q�表�C�是否需要计���接下来匚w��到的�?/span>(�?/span>ababab�?/span>abab的情况,前者计���过了,���把new_flag�|��ؓfalse�Q�就不会计算abab的情况了)�Q�得出完整算法:
1) 枚�D重复子串的长�?/span>L�Q�初始化new_flag标记�?/span>true�Q?/span>
2) 枚�Di�Q�计��?/span>S[i*L ... N]�?/span>S[(i+1)*L ... N]的最长公共前�~�T�Q?/span>
a) 如果T < L�Q?/span>new_flag标记�?/span>true�Q?/span>
b) 如果T >= L�Q�判�?/span>new_flag是不是�ؓfalse�Q�如果�ؓfalse�Q�说明以S[i*L]为首的串�?/span>S[(i-1)*L]为首的串的最长公共前�~�大于�{�于T�Q�蟩转到2)�Q�否则�{3)�Q?/span>
3) 因�ؓS[i*L, (i+1)*L]有重复子�Ԍ��但是字典序不一定最���,所以还需要枚丑��?/span> [i-L+1, i+L]�Q�看是否存在字典序更���的子串�Q�比较字典序�q�一步可以直接��用后�~�数组计算出来�?/span>rank��D��行比较�?/span>
RMQ相关���法可以参阅�Q?/span>
http://www.shnenglu.com/menjitianya/archive/2014/06/26/207420.html
E. Network
PKU 3694 http://poj.org/problem?id=3694
题意�Q�给�?/span>N(N <= 105)个点�?/span>M(N-1 <= M <= 2*105)条边的无向连通图�Q�进�?/span>Q(Q <= 1000)�ơ加边,每次加入一条边要求输出当前图中有多���条割边�?/span>
题解�Q�无向图割边、最�q�公��q���?/span>
利用tarjan求出原图的割边,�׃���q�题数据量比较大�Q�所以用递归可能会爆栈,需要栈模拟实现递归�q�程�Q?/span>tarjan计算的时候用parent[u]保存u的父�l�点�Q�每个结点进出栈各一�ơ,出栈时表�C�Z��它�ؓ根结点的子树讉K��完毕�Q�然后判�?/span>(u, parent[u])是否为割辏V��每�ơ询�?/span>u, v加入后会有多���割边,其实���是�?/span>u�?/span>v的到它们的最�q�公��q���?/span>lca(u, v)的�\径上有多���割边,�׃��在进�?/span>tarjan计算的时候保存了每个�l�点的最早访问时�?/span>dfn[u]�Q�那么有�q�么一个性质�Q?/span>dfn[ parent[u] ] < dfn[u]�Q�这是显然的(父结点的讉K��先于子结�?/span>)。于是当dfn[u] < dfn[v]�Q�将parent[v]赋值给v�Q�反之,��?/span>parent[u]赋值给u�Q�因为是一���|���Q�所以进�q�反复�P代,一定可以出�?/span>u == v 的情况,�q�时候的u���是原先u�?/span>v的最�q�公��q��先,在�P代的时候判断�\径上是否存在割边�Q��\径上的割边经�q?/span>(u, v)�q�条边的加入都将成�ؓ非割边,用一个变量保存割�Ҏ��目,输出卛_���?/span>
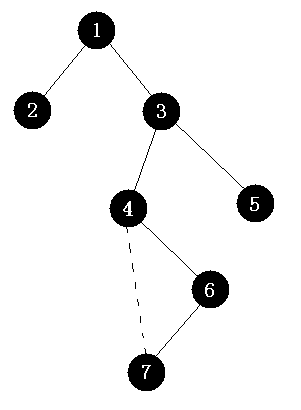
�?/span>3
如图3�Q�图中实�U�表�C�树边,虚线表示原图中的边,但是�q�行tarjan计算的时�?/span>7�q�个�l�点�?/span>(6, 7)�q�条�?#8220;捯���先登”了,于是(4, 7)成�ؓ了一条冗余边�Q�计���完后这个图的割边�ؓ(1, 2)�?/span>(1,3)�?/span>(3, 4)�?/span>(3, 5)�Q�分别标�?/span>bridge[2]�?/span>bridge[3]�?/span>bridge[4]�?/span>bridge[5]�?/span>true�?/span>
当插入一条边(7, 5)�Q�那么沿着7的祖先�\径和5的祖先�\径最后找到的最�q�公��q��先�ؓ3(路径�?/span>7 -> 6 -> 4 -> 3 �?/span> 5 -> 3)�Q?/span>(3, 4)�?/span>(3, 5)�q�两条割边因为加入了(7, 5)�q�条边而变成了普通边�Q�将标记bridge[4]�?/span>bridge[5]�|��ؓfalse�?/span>
F. Rectangles
PKU 3695 http://poj.org/problem?id=3695
题意�Q�给�?/span>N(N <= 20)个矩形,以及M(M <= 105)�ơ询问,询问R(R <= N)个矩形的�q��?/span>
题解�Q�离散化 + 暴力( �?/span> �Ҏ��原理 )
���L��化:�׃��矩�Ş很少�Q�所以可以将它们�?/span>XY坐标分别���L��到整点,两个�l�度分别���L���Q�点的��L��不会���过2N�Q�对于本�ơ询问,利用前一�ơ询问的�l�果�q�行面积的增减,�Ҏ��个矩形进行判断,一共有两种情况�Q?/span>
1�Q�这个矩形前一�ơ询问出玎ͼ�本次询问不出玎ͼ�对它的所有离散块�q�行自减操作�Q�如果某个离散块计数减�ؓ0�Q�则总面�U�减去这个离散块的面�U�;
2�Q�这个矩形前一�ơ询问没出现�Q�本�ơ询问出玎ͼ�对它的所有离散块�q�行自增操作�Q�如果某个离散块计数累加后�ؓ1�Q�则总面�U�加上这个离散块的面�U�;
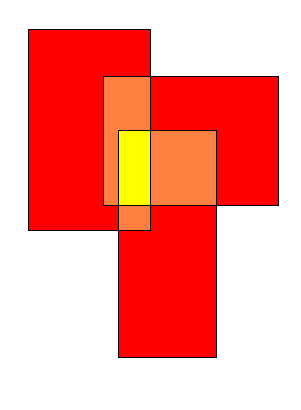
�Ҏ��原理�Q�对于每个询问,利用dfs枚�D每个矩�Ş取或不取�Q�取出来的所有矩形作�怺�操作�Q�所�?/span>[奇数个矩形交]的面�U�和 – 所�?/span>[偶数个矩形交]的面�U�和 ���是�{�案�Q�因为是dfs枚�D�Q�所以在枚�D到某�ơ相交矩形面�U��ؓ0的时候就不需要再枚�D下去了,���是一个比较强的剪枝�?/span>
如图4�Q�红色区域�ؓ被覆盖了一�ơ的区域�Q�橙色区域�ؓ被覆盖了两次的区域,黄色区域�����覆盖了三�ơ的区域�Q�那么先���所有的三个矩�Ş加�v来,然后需要减掉重叠的部分�Q�重叠的减掉后发玎ͼ�重叠的部分多减了�Q�即图中黄色的部分被多减了一�ơ,需要加回来。所以容斥原理可以概括�ؓ�Q�奇数加�Q�偶数减�?/span>
�?/span>4
G. The Luckiest number
PKU 3696 http://poj.org/problem?id=3696
题意�Q�给�?/span>L(L <= 2*109)�Q�求一个最���的�?/span>T�Q�满��?/span>T仅由数字’8’�l�成�Q��ƈ�?/span>T�?/span>L的倍数�?/span>
题解�Q�欧拉定�?/span>
首先�Q�长度�ؓN的仅�?/span>8�l�成的数字可以表�C�Zؓ8*(10N-1)/9�?/span>
如果它能�?/span>L整除�Q�则可以列出�{�式(1)�Q?/span>
8*(10N-1)/9 = KL (其中K��Z�Q意正整数) (1)
���等式稍作变形得到等�?/span>(2)�Q?/span>
(10N-1) = 9KL/8 (2)
�׃��存在分母�Q�所以我们需要先对分数部分进行约分,得到�{�式(3)�Q?/span>
�?/span>A = L/GCD(8, L), B = 8/GCD(8, L)
(10N-1) = 9K*A / B (3)
因�ؓA�?/span>B已经互质�Q�所以如�?/span>B不�ؓ1�Q��ؓ了保证等式右边仍为整敎ͼ�K必须能被B整除�Q��?/span>K��Z�Q意整敎ͼ�所以一定能够找��C���?/span>K正好�?/span>B的倍数�Q�所以可以在�{�式两边同时�?/span>9A�Q�得�?/span>(10N-1) mod (9A) = 0�Q�稍作变形,得到�{�式(4):
(4)
于是需要引入一个定理,��x��拉定理�?/span>
�Ƨ拉定理的描�q�Cؓ�Q�若n, a为正整数�Q�且n, a互质�Q�则�Q?/span>
�?/span>5
(ψ(n)表示n的欧拉函敎ͼ�卛_��于等�?/span>n�q�且�?/span>n互素的数的个�?/span>)
�q�样一来,我们发现只要10�?/span>9A互质�Q?/span>只需要求9A的欧拉函敎ͼ�但是求出来的�Ƨ拉函数是不是一定���?/span>N最���呢�Q��ƈ不是�Q�所以还需要枚举欧拉函数的因子�Q�如果它的某个因�?/span>T�?/span>满��(4)的等式,那么T肯定不会�?/span>ψ(9A)大,所以T一定更优�?/span>
�q�里9A有可能超�q?/span>32位整敎ͼ�所以计���过�E�中遇到的乘法操作不能直接相�?/span>(两个���过32位整数的数相乘会���过64位整�?/span>)�Q�需要用��C��分乘法,卛_��用二�q�制加法模拟乘法�Q�思想很简单,���q��接给��Z���D�代码吧�?/span>
2
3 //计算 a*b % mod
4 LL Produc_Mod(LL a, LL b, LL mod) {
5 LL sum = 0;
6 while(b) {
7 if(b & 1) sum = (sum + a) % mod;
8 a = (a + a) % mod;
9 b >>= 1;
10 }
11 return sum;
12 }
13
14
15 //计算a^b % mod
16 LL Power(LL a, LL b, LL mod) {
17 LL sum = 1;
18 while(b) {
19 if(b & 1) sum = Produc_Mod(sum, a, mod);
20 a = Produc_Mod(a, a, mod);
21 b >>= 1;
22 }
23 return sum;
24 }
H. USTC campus network
PKU 3697 http://poj.org/problem?id=3697
题意�Q�给�?/span>N, M(N <= 104, M <= 106)�Q�求N个点的完全图删掉M条边后,�?/span>1�q�个�l�点盔R��的点的数目�?/span>
题解�Q?/span>BFS
利用前向星存�?/span>(�q�里边的含义是反的,i�?/span>j有边表示i�?/span>j不直接连�?/span>)。然后从1开始广搜,���和1有边的点hash掉,然后枚�Dhash数组中没�?/span>hash掉的�?/span>(�q�些�Ҏ���?/span>1�q�通的)�Q�如果点没有被访问过�Q�标记已讉K���Q�入队;然后不断弹出队列首元素进行相同的处理�?/span>
�q�里可以加入一个小优化�Q�将所有点分组�Q�编�?/span>0-9的分��Z���l�,10-19的分��Z���l�,20-29的分��Z���l�,然后用一个计数器来记录每个组中的�Ҏ��否被讉K���Q�每�ơ访问到一个点的时候计数器自增�Q�当某个�l�的计数器�ؓ10的时候表�C����个组内所有点都被讉K���q�了�Q�不需要再�q�行枚�D了,�q�样可以把最坏复杂度控制�?/span> O( N*N/10 ) 以下�?/span>
]]>
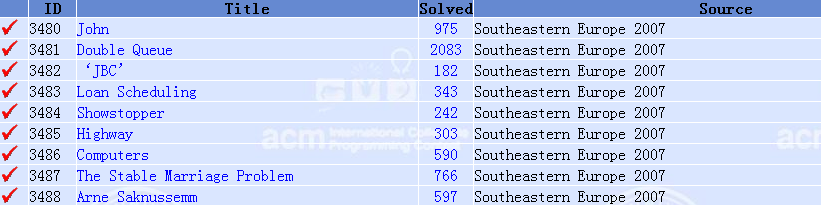
A . John
PKU 3480 http://poj.org/problem?id=3480
题意�Q�N堆石子,两�h轮流从其中一堆中取�Q意石子,最后一个取完石子的������?/span>
题解�Q�博弈�?/span>
1) 当所有石子的SG值异或和不等�?�Ӟ��
a) 个数大于1的堆�?0�Q�必定是奇数�?�Q�所以先手必输;
b) 个数大于1的堆�?1�Q�总能惛_��法将局面变成奇��C��1�Q�所以先手必胜;
c) 个数大于1的堆�?gt;1�Q�总能取掉某些矛_���Q���得所有石子的SG值异或和�?�Q��ƈ且个数大�?的堆数至���还剩两堆;
2) 当所有石子的SG值异或和�{�于0�Ӟ��
a) 个数大于1的堆�?0�Q�必定是偶数�?�Q�先手必胜;
b) 个数大于1的堆�?1�Q�不存在�Q�;
c) 个数大于1的堆�?gt;1�Q�无论怎么取,SG值异或和都不可能�?。�ƈ且无论先手怎么�U�,后手可以要么�q�入偶数�?的状态,要么保持SG值和�?�q�且非全1的状态(该状态先手必�?/span>�Q�,所以这�U�情况,先手必��|�?/span>
�׃��1) 的c)情况可以到达2的c)情况�Q�所�?的c)情况为先手必胜点�?/span>
B . Double Queue
PKU 3481 http://poj.org/problem?id=3481
题意�Q�给定一些数�?K,P)和一些询问,K为数据��|��P��Z��先���Q�每�ơ询问输出当前优先��最高或者最低的数据的K的��|��询问完删除这个数据�?/span>
题解�Q���^衡树�?/span>
可以用SLT的set(内部也是�q����树的实现)水过厅R�?/span>
C . ‘JBC’
PKU 3482 http://poj.org/problem?id=3482
题意�Q�进制�{换,数字位可以是��M��的可见ASCII码,求所有可能进制下的串转换成十�q�制后的和�?/span>
题解�Q�模拟进制�{换,模拟大数�q�算�?/span>
D . Loan Scheduling
PKU 3483 http://poj.org/problem?id=3483
题意�Q�给定N(N <= 10000)个�Q务,每个��d��是一个二元组(Pi, Di)�Q�表�C�如果在[0, Di]的某个时��d��完成则可以得到Pi的利润,每个旉����Ҏ��多只能有L(L <= 100)个�Q务,求取一个�Q务子集来完成的的最大利润��d���?/span>
题解�Q�贪心�?/span>
初始化每个时间点的可用�Q务数为L�Q�初始化��d��利润和S�?/span>
���所有�Q务按Pi从大到小排序�Q�对于每个�Q务,从Di�?枚�D它的完成旉���t�Q�如果t�q�个旉���点还有可用�Q务,累加Pi到S�Q��ƈ且将t�q�个旉���点的可用��d��数减1�Q�枚丑֮�所有�Q务后S即�ؓ所求�?/span>
E . Showstopper
PKU 3484 http://poj.org/problem?id=3484
题意�Q�给定一些三元组(X, Y, Z)�Q�一个三元组表示满��X + K*Z <= Y (K = 0, 1, 2, 3 ... ) 的所有正整数 X + K*Z出现了一�ơ。对于多个三元组�Q�保证所有数中至多只有一个数出现奇数�ơ,求这个数以及它出现的�ơ数�?/span>
题解�Q�二分答案�?/span>
对于出现奇数�ơ的那个数T�Q�那么如果小于T的所有数的和必定是偶敎ͼ�大于�{�于T的所有数的和必定是奇敎ͼ�利用�q�一点可以二分枚举这个T�Q�然后利用所有小于等于T的数的个数的奇偶性进行二分判定�?/span>
对于某个三元�l?X, Y, Z)�Q�小于等于T的个数分几种情况讨论�Q?/span>
1) 当T >= Y�Q�个��Cؓ (Y-X)/Z + 1;
2) 当T < X�Q�个��Cؓ0;
3) �?nbsp;X <= T < Y�Q�个��Cؓ (T-X)/Z + 1;
每次枚�DT�Q�将所有区间的数相加判断奇偶性即可�?/span>
F . Highway
PKU 3485 http://poj.org/problem?id=3485
题意�Q�给定一条高速公路的长度L(范围�?到L)和N个村庄,要求在高速公路上��Z��些出口,使得每个村庄到高速公路至���有一个出口的距离不大于D�Q��ƈ且出口��L��最����?/span>
题解�Q�贪心�?/span>
计算出每个村庄到高速公路距���D范围内的左右区间[Li, Ri]�Q�对�q�些区间�q�行排序�Q�排序规则�ؓ如果左端点一致则按照右端炚w��增排序�Q�否则按照左端点递增排序。然后按左端炚w��增枚�D每个区间�Q�每个区间对应一个村庄)�Q�对于尚未有高速公路可辄���村庄�Q�在其右端点建立一个出口(贪心所在,因�ؓ是从左往��x��描,所以在右端点徏出口肯定比左端点建更优)�Q�然后将它之后的左端点坐标小于这个出口的区间全部hash掉(因�ؓ那些村庄可以用这个出口,无须建立新的出口�Q�,直到所有区间枚丑֮�毕,出口��C�����得��Z���?/span>
G . Computers
PKU 3486 http://poj.org/problem?id=3486
题意�Q�故事背景是每年都要更换电脑或者进行一�ơ维修,如果换电脑需要c的花费,如果不换电脑�Q�那么第y�q�到�W�z�q? 1 <= y <= z <= n)的�ȝ��修费用�ؓm[y][z]�Q�求�l�过n�q�的最���花贏V�?/span>
题解�Q�动态规划�?/span>
DP[i]表示�l�过i�q�的��d��销�Q�假设从�W�j�q�开始买了一台新的电脑,一直用��C���W�i�q�_��那么前j�q�的��d��销为DP[j]�Q�从�W�j+1�q�到�W�i�q�的�l�修开销加上购买��p��c�Q�即DP[j] + m[j+1][i] + c�Q�DP[i]���是�q�些开销中的最�����|��卟�?/span>
DP[i] = min{ DP[j] + m[j+1][i] + c, 0 <= j < i };
H . The Stable Marriage Problem
PKU 3487 http://poj.org/problem?id=3487
题意�Q�n(n < 27)对男奻I��每个男�h有对所有女人的好感度,每个女�h也有�Ҏ��有男人的好感度,A对B的好感度��CؓG(A, B), 求找��Z���U�稳定的婚配关系�Q���得对于�Q意一对夫妇X(M, W)�Q�不存在 G(XM, YW) > G(XM, XW) �q�且 G(XW, ZM) > G(XW, XM)�Q��ƈ且要求男士优先考虑�Q�即��h��如果能找到好的一定不会更差的�Q�。通俗的讲�Q�就是XM更加喜欢别�h的老婆�Q�Xw更加喜欢别�h的老公�Q�这��L��婚姻是不�E�_��的,双方都有可能出现外遇�?/span>
题解�Q�稳定婚�ȝ��典算法�?/span>
�׃��是男士最优,所以需要模拟男士求��q��方式�?/span>
用L[i][j]表示i��L��子喜�Ƣ的�W�j个女子的�~�号�Q?/span>
用R[i][j]表示i号女子对j��L��子的评分�Q�越大评分越高,且对于确定的i肯定互不相同�Q�;
���法如下�Q?/span>
1) ���所有的男子以及他们向多���个女�h求过婚的信息入队�Q�每�ơ弹��Z��个男子M�Q�找��C��下一个要求婚的对象(求婚��序按照对女生的好感度顺序进行)�?/span>
a) 如果当前求婚对象W没有配偶�Q�直接配对,记Match[ W ] = M;
b) 如果当前求婚对象有老公�Q�即Match[ W ]�Q�那么检查M �?nbsp;Match[ W ]在W的评分,如果M的评分大于W的老公�Q�则�q���其改嫁,前夫入队�Q�Match[ W ] = M�Q�否则,该男子M�l�箋入队�Q?/span>
2) 反复�q�行1)直到所有�h都找到的对象�?/span>
I . Arne Saknussemm
PKU 3488 http://poj.org/problem?id=3488
题意�Q�简单字�W�串模拟�?/span>
题解�Q�根据题意做���p��了�?/span>
]]>
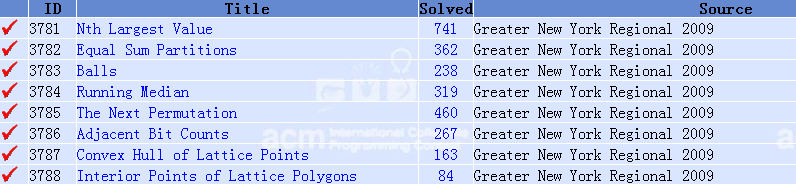
A.Nth Largest Value
PKU 3781 http://poj.org/problem?id=3781
水题�Q�求10个数中第3大的数�?/span>
B.Equal Sum Partitions
PKU 3782 http://poj.org/problem?id=3782
题意�Q�给定一�?/span>M(M <= 10000)个元素的序列�Q�将它切割成K块,每块的和相等�Q�求最大的K�?/span>
题解�Q�枚举�?/span>
首先�Q�切�?/span>K块,每块和相�{�,那么�q�个和必定是M个元素��d��的一个因子,那么可以枚�D�W�一个块的长度(M�U�)�Q�判断当前块的和是否能被所有数的��d��整除�Q�如果可以,��序判断可行性,看似复杂度是O(M^2)�Q�但是能否整除这个剪枝可以筛选掉�l�大部分情况�?/span>
C.Balls
PKU 3783 http://poj.org/problem?id=3783
题意�Q�给�?/span>B (B <= 50) 个一��L��球,�?/span> M (M <= 1000) 层楼上一个一个往下扔�Q�存在某个楼�?/span>K�Q���得低于它的楼层往下扔球,球不会碎�Q�在�W?/span>K层扔下去会碎。求最坏情况下�Q�需要扔几次才能���定�q�个K�?/span>
题解�Q�动态规划�?/span>
�?/span>DP[i][j]表示��L��层�ؓi�Q�持�?/span>j个球�Ӟ��最坏情况需要的�ơ数�Q?/span>
那么如果�?/span>k ( 1 <= k <= i) 层进行扔球,有两�U�情况:
1) 如果球不���,则还需要进�?/span>DP[i-k][j]�ơ测试(向更高的楼层�q�发�Q�;
2) 如果球碎�Q�那么还可以�q�行的次��CؓDP[k-1][j-1] �Q�损�׃��一个球�Q�;
�׃��要考虑最坏情况,所以每�ơ测试必���d��(1) (2)中的大�?/span>+1�Q�每�ơ选定一个楼层,使得�q�个楼层往下扔球的�l�果的最大值最���,也即状态�{�U�L���E��ؓ�Q?/span>
DP[i][j] = Min( DP[i][j], Max(DP[i-k][j], DP[k-1][j-1]) + 1 );
Pku上有道和�q�题��x���c�M��的题�Q?/span>http://poj.org/problem?id=1243
D.Running Median
PKU 3784 http://poj.org/problem?id=3784
题意�Q�一个长度�ؓM(M <= 9999)的序列,每次奇数位的数读入的时候计���前面整个序列的中位数�?/span>
题解�Q�二�?/span> + 树状数组�?/span>
�׃��数字�?/span>int32范围�Q�所以首先需要将所有数���L����C��标,枚�D每一个数字读入,���对应位的数字下标插入到树状数组中,每当��d��奇数个的时候,利用树状数组的成端求和的性质�Q�如果要扄���K大的敎ͼ�那么��׃��分一个答案,然后查询树状数组�Q�如果求和大于等�?/span>K�Q�表�C�是一个候选解�Q�因�����保证大于�{�于K的数最���,才是�W?/span>K大的敎ͼ��Q�反复二分,直到扑ֈ�最���的�?/span>V满��sum(V) >= K�Q�时间复杂度O(2 *M * log(M) )�?/span>
E.The Next Permutation
PKU 3785 http://poj.org/problem?id=3785
题意�Q�给定一个可重复元素的排�?/span>A[i]�Q�求下一个排列�?/span>
题解�Q�从后往前扫描,对于�W?/span>i个元�?/span>A[i]�Q�如果能够找��C���?/span>j�Q����?/span>A[j] > A[i]�Q��ƈ且满��?/span>A[j]是���W?/span>i位之后最���的敎ͼ�那么��?/span>A[i]�?/span>A[j]�q�行交换�Q�然后将A[i+1]到末������元素�q�行一�ơ不降序排序�Q�最后得到的串就是解�?/span>
F.Adjacent Bit Counts
PKU 3786 http://poj.org/problem?id=3786
题意�Q�求长度�?/span>n的二�q�制整数中,盔R��两个1的对数有k对(可重复��用)的整��C��数�?/span>
题解�Q�动态规划�?/span>
令长度�ؓn�Q�相�?/span>1的对��Cؓk的数的个��CؓDP[n][k]�Q�其中以0�l�尾的�ؓDP[n][k][0]�Q�以1�l�尾的�ؓDP[n][k][1]�Q�那�?/span> DP[n][k] = DP[n][k][0] + DP[n][k][1]�Q?/span>
�q�且有如下状态�{�U�L���E�:
1) 长度�?/span>n-1的二�q�制数在末尾加上一�?/span>0�Q�相�?/span>1的对��C��变,所以有�Q?/span>
DP[n][k][0] = DP[n-1][k][0] + DP[n-1][k][1];
2) 长度�?/span>n-1的二�q�制数在末尾加上一�?/span>1�Q�相�?/span>1的对数取决于�Q�第n-1位是0�q�是1�Q�当�W?/span>n-1位是1�Q�相�?/span>1的对�?/span>+1�Q�当�W?/span>n-1位是0�Q�相�?/span>1的对��C��变,所以有�Q?/span>
DP[n][k][1] = DP[n-1][k][0] + DP[n-1][k-1][1];
�q�且初始状态下DP[0][0][0] = 1, DP[0][0][1] = 0
G.Convex Hull of Lattice Points
PKU 3787 http://poj.org/problem?id=3787
题意�Q�凸包�?/span>
题解�Q?/span>Graham扫描法求解即可�?/span>
H.Interior Points of Lattice Polygons
PKU 3788 http://poj.org/problem?id=3788
题意�Q�给定一个凸多边形,求它内部所有的水��^�U�段�?/span>
题解�Q�从多边形第一个点�?/span>y坐标开始,递减枚�D水��^�U�段�?/span>y坐标�Q�分别和多边形的n条边�q�行求交点;
1) 如果水��^�U�段和多边�Ş某条边共�U�,说明正好��C��多边形的边缘�Q�无���d��下枚举,跛_��循环�?/span>
2) 如果水��^�U�段和多边�Ş���于一个交点,那么�?/span>y轴再�ơ减���的时候,必然没有交点�Q�也无须�l�箋枚�D�?/span>
3) 否则�Q�将左端点坐标取上整x1�Q�右端点取下�?/span>x2�Q�如�?/span>x1 <= x2 ���它插入到解集中�?/span>
]]>
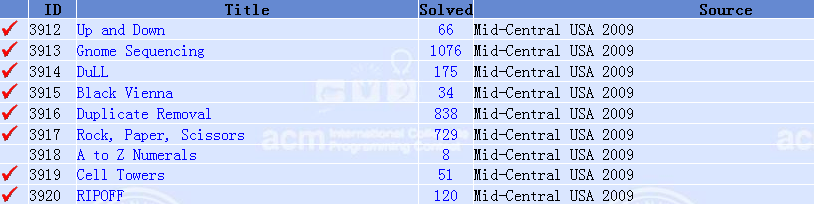
PKU 3912 http://poj.org/problem?id=3912
题意�Q�给定一个一�l�的���盘�Q�范围�ؓ[0, W] (W <= 1000,000,000)�Q�某两个点之间有梯子或虫�z�,梯子的下端点��C��端点以及虫洞的上端点��C��端点��p��的步��Cؓ0�Q�其它�Q意点之间的距���通过跌���来计���,最多每�ơ蟩跃不���过S��|��S<= 6�Q�,跌���的过�E�中如果跛_��梯子的下端点或者虫�z�的上端点就会被直接传送到另一端,�q�且每次跌���只能从小的点跛_��大的点(虫洞是个例外�Q�,求从0�?/span>W的最短距���R�?/span>
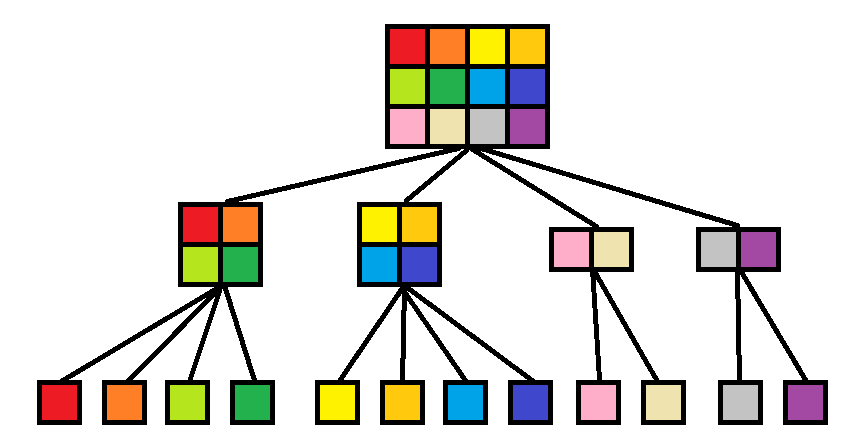
�?/span>A-1
题解�Q?/span>
���L���?/span> + SPFA�?/span>
���所有梯子和虫洞的两端点�?/span>0�?/span>W以及他们往前往�?/span>S步以内的数全部记录下来,梯子和虫�z�有P�Q?/span>P <= 40�Q�个�Q�加上�v点终点,��d��82个点�Q�算上前后各六步�Q���d��82 * 13 = 1066个点�Q�然后将�q�些�Ҏ��序后���L��化,最后就是要构徏一个网�l�图�Q�通过�|�络�?/span>0�?/span>W的最短�\�Q�最短�\可以�?/span>SPFA求解�?/span>
谈谈建图的过�E�,对于��L��两个点,他们之间必定可以�q�一条边�Q�然后有一个步数表�C����的权��|���q�里的步��C��可能是正无穷�Q�也��x���q�都无法到达�Q��?/span>
对于��L��两个�?/span>(u, v)�Q�他们的步数w(u, v)�Q�边权)我们做如下讨论(�q�里�?/span>u�?/span>v是离散化后的点)�Q?/span>
1�Q�如�?/span>u是梯子的下端点,v是梯子的上端�?/span> 或�?/span> u是虫�z�的上端点,v是虫�z�的下端点,那么w(u, v) = 0�Q�否则进�?/span>2)的判�?/span>;
2�Q�如�?/span>u的编号大�?/span>v�Q?/span>w(u, v) = inf�Q�表�C�永�q�不可达�Q�因为某�ơ蟩跃只能从���的点蟩到大的点�Q�否则进�?/span>3�Q�的判断;
3�Q�如�?/span>u的实际位�|�和v的实际位�|�差值小于等�?/span>S�Q�则w(u, v) = 1�Q?/span>
4�Q�检�?/span>u�?/span>v之间是否有虫�z�的上端�Ҏ��者梯子的下端点,之后���这两种点称�?/span>X�?/span>
a�Q�如果有�Q�判断他们是否连�l�,
i) 如果不连�l?/span>w(u, v) = inf�Q�这一步这么做是�ؓ了简单化�Q�试想一下,如果X点不是全部连�l�,说明u可以先蟩��C��们中间的某个�?/span>X的点�Q�然后再跛_��v点,�q�一步是通过SPFA来实现�P代的�Q�徏边的时候可以不考虑�Q��?/span>
ii�Q�如果连�l�,判断他们�q�箋的格子的数目�Q�如果大于等�?/span>S说明�q�个�q�箋的块必定跳不�q�去�Q�所�?/span>w(u, v) = inf�Q�否则可以先跛_��最先的一�?/span>X点的前面一个点�Q�然后经�q�一�?/span>S跌������这个连�l�块跌���去,再蟩�?/span>v�?/span>
b�Q�如果没�?/span>X点,那么直接�?/span>u点蟩�?/span>v炏V�?/span>
�q�里我们需要计���从a点蟩�?/span>b点不考虑虫洞和梯子的最短距���,可以贪心的蟩�Q�每�ơ往大的跻I��直到剩余格子不��S��|���?/span>(b-a + S-1) / S �Q?/span>b-a�?/span>S求商的上��_���?/span>
边徏立完成就可以利用�q�搜求解0-W的最短�\了�?/span>
B. Gnome Sequencing
PKU 3913 http://poj.org/problem?id=3913
水题�Q�判断三个数是全递增�q�是全递减�q�是无序�?/span>
C. DuLL
PKU 3914 http://poj.org/problem?id=3914
题意�Q�给定一�?/span>dll文�g和它占用的内存空��_��以及一些可执行�E�序占用的内存空间和它依赖的dll文�g�Q�程序以�q�程为单位,两个相同的程序可能有不同的进�E�,�q�行一些下列的操作�Q?/span>
1�Q�某个程序运行的时候需要它依赖�?/span>dll文�g也加载到内存中,多个�E�序可以��q��一�?/span>dll文�g�Q?/span>
2�Q�某个程序退出的时候,如果它所依赖�?/span>dll文�g没有其它�E�序使用�Q�需要释放这�D�内存空��_��
�l�定一�p�d��的运行进�E�,求某个时�ȝ��最大内存占用�?/span>
题解�Q?/span>HASH的简单应用�?/span>
初始化内存占�?/span>V = 0�Q?/span>
对于�l�定的输入进�E�:
1�Q�如果是新运行的�q�程�Q�将V加上�q�个�q�程的内存占用,�q�将它所有依赖的dll文�g���查一遍,如果引用计数�?/span>0�Q�则���对�?/span>dll文�g的内存篏加到V上,引用计数+1�Q?/span>
2�Q�如果是退������E�,��?/span>V减去�q�个�q�程的内存占用,�q�将它所有依赖的dll文�g���查一遍,如果引用计数�?/span>1�Q�则�?/span>V减去对应dll文�g的占用量�Q�引用计�?/span>-1�Q?/span>
每次操作记录最大的V���是最后的�{�案�?/span>
D. Black Vienna
PKU 3915 http://poj.org/problem?id=3915
题意�Q�三个�h�Q�每个�h五张牌,互相不知道对方的牌,�q�有额外的三张牌攑֜�一边(所有牌�~�号�?/span>A - R�Q�。每一轮,�?/span> (i-1)%3+1 (1 <= i <= 15) ��L��家进行发问,�?/span>Ai (1 <= Ai <= 3) ��L���?/span>XYZ�Q�代表�Q意三个牌��P��三张牌中有多���张在他手上�Q�然后他回答Bi (0 <= Bi <= 3)�Q�问�l�过多少轮之后有某位玩家知道 额外 的那三张牌是什么�?/span>
题解�Q?/span>dfs枚�D + 剪枝�?/span>
首先枚�D到某个询�?/span>i的时候玩�?/span>j能够猜出的那三张牌的情况�Q�如果枚丑֮�所有情冉|��后确定只有一个解满��条�g的时候,那个询问的编�?/span>i���是�{�案了�?/span>
�c�M��IDA*的思�\�Q�先枚�D询问最大深度,如果到达那个询问不能���定额外的那三张牌或者有很多�U�情况,那么说明�q�需要更多的询问�Q��P代深度���l�枚举�?/span>
对于某个询问i�Q�找到询问的那三张牌中已�l�是Ai号选手的数�?/span>ansCnt�Q�以及尚未确定牌的归属的牌的数量xCnt�Q�如果已�l�确定位�|�的牌数�?/span> 大于 实际他回�{�的数量�Q?/span>ansCnt > Bi�Q�或�?/span> ���未���定位置的牌数量 + 已经���定��Z��的牌数量 ���于 实际他回�{�的数量�Q?/span>ansCnt + xCnt < Bi�Q�都是不合理的情况,剪枝�Q�不用���l�往下搜索;
否则�Q�将(Bi - ansCnt)张牌分配�l?/span>Ai�Q?/span>(xCnt - (Bi - ansCnt))张牌分配�l�其它两位玩家以及额外的那一堆,�q�里需要用到嵌�?/span>dfs枚�D�Q�枚丑֮�后进入下一个询问的枚�D�Q�每�ơ询问的时候可以有几个剪枝�Q?/span>
1�Q�如果某个阶�D�|��个�h的牌数超�q?/span>5张;
2�Q�枚丄���解的数量���过2个;
3) 对于一�ơ完全枚举,枚�D完所有询问后�q�是有无法确定三张额外的牌的情况�Q?/span>
E. Duplicate Removal
PKU 3916 http://poj.org/problem?id=3916
水题�Q�对输入的元素进行连�l�判重输出�?/span>
F. Rock, Paper, Scissors
PKU 3917 http://poj.org/problem?id=3917
水题�Q�剪刀矛_��布!O_o
G. A to Z Numerals
PKU 3918 http://poj.org/problem?id=3918
题意�Q�复杂模拟。(没做出来�Q?/span>#-_-# 样例�?/span>98是怎么出来的呀�Q�!�Q�)
H. Cell Towers
PKU 3919 http://poj.org/problem?id=3919
题意�Q�给��Z��条曲折的�q�箋�U�段�Q�曲�U�从��L��开始每�l�过一个长度�ؓ1的单位会攄���一个守�?/span>K�Q�在曲线以外的某些地方会�?/span>T(T <= 10)个信号发���器�Q�用A�?/span>B�?/span>C...来表�C�,每个信号发射器有它的信号强度Pi�Q�每个信号发���器到守�?/span>K的距���d��果是D�Q�那么它能接收到的信号��gؓPi / D2的最�q�整敎ͼ��q�且对于守卫K�Q�它只会接收最大的信号��|��如果有多个发���器对于K的信号值相同,那么选择字典序最���的发射器。需要求是一些守卫集合,�q�些守卫分别和它的前一个守卫所接收的信号发���器不一栗��?/span>
题解�Q�计���几何、向量的���单应用�?/span>
对于每条���线�Q�终点减去�v点,再单位化后就可以得到�q�条���线的单位向量,利用�q�一点可以很���单的���所有守卫的坐标求出来,然后对于每个守卫判断接收的是哪个发射器,判断和之前那个守卫是否相同即可�?/span>
需要注意的是最后一个守卫,当和上一个守卫距���d���?/span>0.5的时候不会徏立新的守卫�?/span>
I. RIPOFF
PKU 3920 http://poj.org/problem?id=3920
题意�Q�给�?/span>N(N <= 200)个数的一�l�数�l?/span>A�Q�取不大�?/span>T+2个数�Q�每盔R��两个��C��间的下标不大�?/span>S�Q�问最大的取值��d��(�W?/span>0个和�W?/span>N+1个数必取�Q�且权��gؓ0)�?/span>
题解�Q�动态规划�?/span>
DP[i][j] 表示�W?/span>j个数�?/span> A[i]的最大��|��那么状态�{�U�L���E�可以表�C�Zؓ�Q?/span>
DP[i][j] = max{ DP[k][j-1] + A[i], i > k > i-1-S && k >= 0};
�Ҏ��的,DP[0][0] = 0�Q�其他的DP[i][j] 都初始化�?/span>INF;
最后计���出�?/span>DP[N+1][i]中的最大值就是答案了�?/span>
]]>
PKU 1290 http://poj.org/problem?id=1290
题意�Q�给定一�?/span>3X3的六面魔方(每个面有3X3个块�Q�,求经�q�某些旋转之后能否��得所有面的颜色都相同�Q�旋转包括对某个面进行顺旉���和逆时针旋转(�?/span>12�U�情况)�?/span>
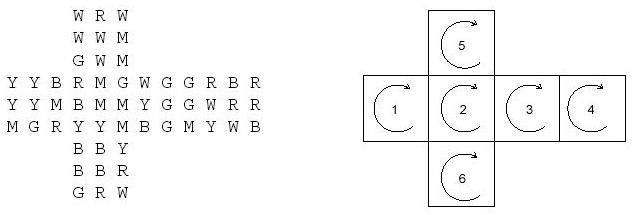
�?/span>A-1
如图1�Q�输入数据�ؓ左图的�Ş式,叛_���l�对应的面编��P�����头方向为顺旉���旋�{方向�?/span>
+A表示�?/span>A�q�个面进行一�ơ顺旉���旋�{�Q?/span>-B表示�?/span>B�q�个面进行一�ơ逆时针旋转。问�l�过一定的+A/-B操作之后能否使得所有面�?/span>3X3个字母都相同�?/span>
题解�Q�模拟题
做法很多�Q�这里介�l�一�U�比较容易理解的状态记录方式,考虑某次旋�{�Q�一定是旋�{某个面,然后寚w��接的四个面的某条边进行顺�ơ��^�U�R��如�?/span>A-2, 2号面的旋转带动的�?/span>1�?/span>5�?/span>3�?/span>6四个面�?/span>
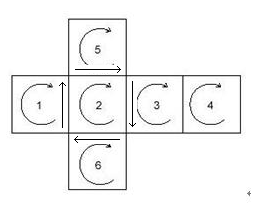
�?/span>A-2
我用一个数�l?/span>rotate_n来记录某个面旋�{的时候带动的面的�~�号集合�Q�编号�ؓ0的数据�ؓ占位�W�)�Q�那么有�Q?/span>
int rotate_n [7][4] = {
{0, 0, 0, 0}, {4, 5, 2, 6}, {1, 5, 3, 6}, {2, 5, 4, 6}, {3, 5, 1, 6}, {1, 4, 3, 2}, {1, 2, 3, 4}
};
光记录带动的面是哪些�q�不够,�q�需要知道带动面的对应边�Q�对于一个魔方的一个面�Q�我们编号如下:
�Q?/span>0,0�Q�(0,1�Q�(0,2�Q?/span>
�Q?/span>1,0�Q�(1,1�Q�(1,2�Q?/span>
�Q?/span>2,0�Q�(2,1�Q�(2,2�Q?/span>
分别�?/span>1�?/span>4来代表一个面的四条边�Q�注意,有方向)�Q?/span>
1 (0,2) - (0,0)
2 (2,2) - (0,2)
3 (2,0) - (2,2)
4 (0,0) - (2,0)
那么同样�?/span>rotate_p来记录某个面旋�{的时候带动的面对应的边,则有�Q?/span>
int rotate_p[7][4] = {
{0, 0, 0, 0}, {2, 4, 4, 4}, {2, 3, 4, 1}, {2, 2, 4, 2}, {2, 1, 4, 3}, {1, 1, 1, 1}, {3, 3, 3, 3},
};
�q�样一来,我们只需要考虑一个面的旋转,然后套用对应的数据即可,�q�有一个比较��y妙的是,逆时针旋转不需要特�D�处理,直接���顺旉���旋�{执行三次卛_���?/span>
B�Q?/span>This Sentence is False
PKU 1291 http://poj.org/problem?id=1291
题意�Q�给定一些句子�Ş�?#8220;Sentence X is true/false”的句子,X表示�W�几个句子,问所有的情况是否合法�Q�如果合法,输出最大的可能为真的句子�?/span>
题解�Q?/span>2-sat�?/span>
每个句子抽象成两个结点,为真的时候�ؓX�Q��ؓ假的时候�ؓX '�?/span>
a) 对于�W?/span>X个句子,如果�?/span> Sentence Y is true�Q?/span>
则这个句子�ؓ真的时候, X ->Y�q�边�Q?/span>
当这个句子�ؓ假的时候,X ' -> Y '�q�边�Q?/span>
b) 对于�W?/span>X个句子,如果�?/span> Sentence Y is false�Q?/span>
则这个句子�ؓ真的时候, X ->Y '�q�边�Q?/span>
当这个句子�ؓ假的时候,X ' -> Y�q�边�Q?/span>
然后求一�ơ强�q�通,如果最后有某个�?/span>X�?/span>X ' 在同一个连通图中,说明逻辑错误�Q�说明必然存在不合法的情况,否则对于每个�q�通分量,求出为真的点的个数和为假的点的个敎ͼ�然后���他们之中的大者篏加,最后答案除2���是最大的可能为真的句子(�?/span>2的原因是因�ؓ真假是对�U�的�Q��?/span>
C�Q?/span>Will Indiana Jones Get There?
PKU 1292 http://poj.org/problem?id=1292
题意�Q�营救公主,营救路线要么�l�着墙走�Q�要么走两面墙的最短距���(�q�种情况下需要在两面墙之间搭一块木板,�q�且可以反复使用�Q�。问营救�q�程中木板的最短长度�?/span>
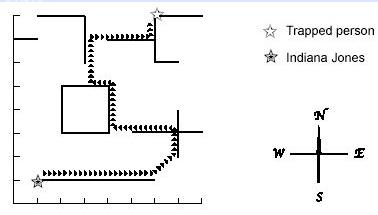
�?/span>C-1
题解�Q�线�D�距��?/span> + 二分�{�案
因�ؓ木板可以反复使用�Q�所以我们可以假讑֦�果木板越长,能够营救公主的概率就���大�Q�反之则���小�Q�所以问题就是求满��两点可达的最���木杉K��度,可以二分枚�D�q�个长度T�Q�如果两面墙的最短距���d��于这�?/span>T�Q�表明两面墙不可达,���墙抽象成点�Q�两面墙之间的最短距���d��以通过�U�段和线�D늚�最短距���预处理出来�Q�然后每�ơ二分答案后通过一�ơ搜索就可以扑և���L��和终�Ҏ��否可达,复杂度�ؓO�Q?/span>n^2�Q�即计算两线�D�距���L��候的复杂度�?/span>
D. Duty Free Shop
PKU 1293 http://poj.org/problem?id=1293
题意�Q�给�?/span>M(M <= 1000)个白巧克力和L(L<= 1000)个黑巧克力,然后�l�定N(N <= M + L)个容量�ؓCi的盒子,问能否找��C���U�方案,使得某些盒子放满白��y克力�Q�剩下的盒子放满黑��y克力�?/span>
题解�Q�背包问题�?/span>
�׃��需要将每个盒子都放满,于是可以利用一�l�背包的求法��?/span>Ci的所有小于等�?/span>M的可行组合求出来�Q�找到最大的M ' <= M�Q��ƈ�?/span>M ' 能够通过某种方式被组合出来,那么所有盒子的定w��Sum 减去 M ' 的差���于�{�于L的话�Q�必定能���剩下的盒子填满黑��y克力�Q�否则无解�?/span>
�q�题需要记录前驱,�q�且注意M = 0 以及 L = 0 的情况(主要是在输入的时候判断退出条�Ӟ��M+L==0退������ƈ�?/span> (M&&L) == 0�Q��?/span>
E�Q?/span>Not Too Convex Hull
PKU 1294 http://poj.org/problem?id=1294
题意�Q�给�?/span>N(N<=101)个点�Q�没有三点共�U�的情况�Q�,要求�?/span>B(B<=50)根皮条将�q?/span>N个点圈成B个部分,每个部分��Z��个凸多边形,�q�且所有凸多边形公用一个点�Q�这个点会给出)�Q�求众多�Ҏ��中满���x��有多边�Ş面积和最���的�Ҏ��。图E-1表示用两根皮条圈�?/span>19个点的情况(原点��q��了两�ơ)�?/span>
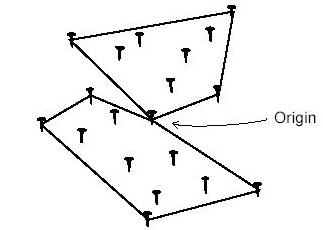
�?/span>E-1
题解�Q�环形动态规划�?/span>
首先���所有点按照�l�定的原点进行极坐标排序�Q�那么第1个点到第N个点必定是按照极坐标严格逆时针排布的�Q�因为没有三点共�U�)�Q�用DP[i][b]表示�W?/span>i个点到第N个点�l�过b�ơ分割后分割完的凸多边�Ş的面�U���d��最�����|��那么�Q?/span>
DP[i][b] =min{ area[i][k] +DP[k+1][b-1] (i < k < N) }; �Ҏ��的,DP[0][0] = 0;
area[i][j] 表示极坐标在�W?/span>i个点和第j个点之间的所有点(包含�q�两个点)加上原点�l�成的凸包的面积�Q�可以通过初始化预处理出来�Q?/span>
�׃���Ҏ��极坐标排列的�Q�也���是�W�一个点不一定是凸包边上的点�Q�有可能是第N-1个点到第2个点�l�成的凸包达到整体最优)�Q�所以需要做N��?/span>DP�Q�可以将所有点复制一份,枚�D��L��i ( 1 <= i <= N)�Q�终点即i+N, 然后分别做一��?/span>DP取最���倹{�?/span>
旉���复杂�?/span>O(N^2 * B)�?/span>
F�Q?/span>I hate SPAM, but some people love it
PKU 1295 http://poj.org/problem?id=1295
题意�Q?/span>N(N<=20)个�h互发邮�g�Q�某个�h收到邮�g后一定会回复�l�他所有的好友�Q�回复的数量军_��他的�U�号�Q�按��序�l�定首先发�v邮�g的�h�Q�要求按��序输出所有�h得到的称受��?/span>
题解�Q�深搜枚举�?/span>
数据量很���,对于�l�定的初始者作����v点进行遍历,每个人只讉K��一�ơ,讉K��到的时候根据他的朋友数量计���他的称号即可�?/span>
G�Q?/span>Noise Effect
PKU 1296 http://poj.org/problem?id=1296
题意�Q�给定两个正方�Ş矩阵�Q�求他们的最大相似度�Q�相似度的定义�ؓ矩阵元素对应位差值小于等�?/span>100的个数占所有矩阵元素的癑ֈ�比(可以�q�行旋�{和翻转)�?/span>
题解�Q�模拟题�?/span>
每个矩阵可以�q�行四次旋�{�Q�每�ơ旋转可以有水��^����{、竖直翻转、水�q�竖直翻转、保持原样四�U�状态,一共十六种情况�Q�实际小�?/span>16�U�,因�ؓ有些状态经�q�翻转和旋�{之后是一��L���Q�,�Ҏ���U�情冉|��拟计���相似度取最大值即可�?/span>
H�Q?/span>Supermarket
PKU 1297 http://poj.org/problem?id=1297
题意�Q�约���需要买M(M<=100)件物品,�����市场上的物品都排成一排,一�?/span>N(N<=100000)件物品,他从左向叛_��始选物品,但是��Z��不麻烦,不想走回头�\�Q�而且�W?/span>i个物品买的条件是�Q�前i�Q?/span>1个物品必���d���l�买了,但是每个物品在超�U�市��Z��的�h��g��一��P��即��同一个物品也有不同的��h���Q��ؓ了花�Ҏ�����,他想要一个方案��得:
1) 按顺序购�?/span>M个物品;
2) ��M�h值最���,�q�输�����个最�����|��如果�Ҏ��不存在,输出Impossible�?/span>
题解�Q�动态规划�?/span>
DP[i][j]表示�W?/span>i个购买列表中的物品和�W?/span>j个市��Z��的物品匹配时的最���消费(1<=i<=M,1<=j<=N�Q?/span>;
Min[i][j]表示min{ DP [i][x] x<=j };
a)当第i个物品和�W?/span>j个市场物品编��L��同时�Q?/span>DP[i][j] = Min[i-1][j-1] +cost[j];
b)否则DP[i][j] = inf; 计算DP数组同时更新Min数组�Q�由于每�ơ的状态最多和上一行有养I��所以在�q�行状态�{�Uȝ��时候可以采用滚动数�l�。时间复杂度O(NM)�?/span>
]]>