A.Grandpa's Rubik Cube
PKU 1290
http://poj.org/problem?id=1290
題意:給定一個(gè)3X3的六面魔方(每個(gè)面有3X3個(gè)塊),求經(jīng)過(guò)某些旋轉(zhuǎn)之后能否使得所有面的顏色都相同,旋轉(zhuǎn)包括對(duì)某個(gè)面進(jìn)行順時(shí)針和逆時(shí)針旋轉(zhuǎn)(共12種情況)。
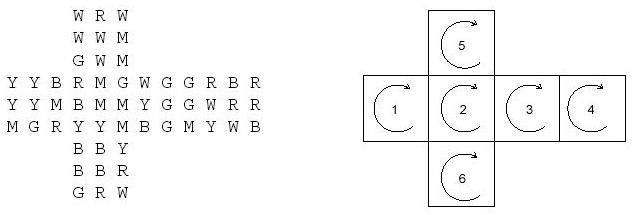
圖A-1
如圖1,輸入數(shù)據(jù)為左圖的形式,右圖給對(duì)應(yīng)的面編號(hào),箭頭方向?yàn)轫槙r(shí)針旋轉(zhuǎn)方向。
+A表示對(duì)A這個(gè)面進(jìn)行一次順時(shí)針旋轉(zhuǎn),-B表示對(duì)B這個(gè)面進(jìn)行一次逆時(shí)針旋轉(zhuǎn)。問(wèn)經(jīng)過(guò)一定的+A/-B操作之后能否使得所有面的3X3個(gè)字母都相同。
題解:模擬題
做法很多,這里介紹一種比較容易理解的狀態(tài)記錄方式,考慮某次旋轉(zhuǎn),一定是旋轉(zhuǎn)某個(gè)面,然后對(duì)鄰接的四個(gè)面的某條邊進(jìn)行順次平移。如圖A-2, 2號(hào)面的旋轉(zhuǎn)帶動(dòng)的是1、5、3、6四個(gè)面。
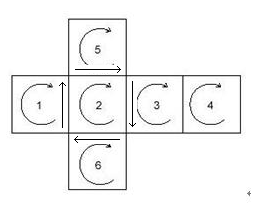
圖A-2
我用一個(gè)數(shù)組rotate_n來(lái)記錄某個(gè)面旋轉(zhuǎn)的時(shí)候帶動(dòng)的面的編號(hào)集合(編號(hào)為0的數(shù)據(jù)為占位符),那么有:
int rotate_n [7][4] = {
{0, 0, 0, 0}, {4, 5, 2, 6}, {1, 5, 3, 6}, {2, 5, 4, 6}, {3, 5, 1, 6}, {1, 4, 3, 2}, {1, 2, 3, 4}
};
光記錄帶動(dòng)的面是哪些還不夠,還需要知道帶動(dòng)面的對(duì)應(yīng)邊,對(duì)于一個(gè)魔方的一個(gè)面,我們編號(hào)如下:
(0,0)(0,1)(0,2)
(1,0)(1,1)(1,2)
(2,0)(2,1)(2,2)
分別用1到4來(lái)代表一個(gè)面的四條邊(注意,有方向):
1 (0,2) - (0,0)
2 (2,2) - (0,2)
3 (2,0) - (2,2)
4 (0,0) - (2,0)
那么同樣用rotate_p來(lái)記錄某個(gè)面旋轉(zhuǎn)的時(shí)候帶動(dòng)的面對(duì)應(yīng)的邊,則有:
int rotate_p[7][4] = {
{0, 0, 0, 0}, {2, 4, 4, 4}, {2, 3, 4, 1}, {2, 2, 4, 2}, {2, 1, 4, 3}, {1, 1, 1, 1}, {3, 3, 3, 3},
};
這樣一來(lái),我們只需要考慮一個(gè)面的旋轉(zhuǎn),然后套用對(duì)應(yīng)的數(shù)據(jù)即可,還有一個(gè)比較巧妙的是,逆時(shí)針旋轉(zhuǎn)不需要特殊處理,直接將順時(shí)針旋轉(zhuǎn)執(zhí)行三次即可。
B.This Sentence is False
PKU 1291 http://poj.org/problem?id=1291
題意:給定一些句子形如“Sentence X is true/false”的句子,X表示第幾個(gè)句子,問(wèn)所有的情況是否合法,如果合法,輸出最大的可能為真的句子。
題解:2-sat。
每個(gè)句子抽象成兩個(gè)結(jié)點(diǎn),為真的時(shí)候?yàn)?/span>X,為假的時(shí)候?yàn)?/span>X '。
a) 對(duì)于第X個(gè)句子,如果是 Sentence Y is true;
則這個(gè)句子為真的時(shí)候, X ->Y連邊;
當(dāng)這個(gè)句子為假的時(shí)候,X ' -> Y '連邊;
b) 對(duì)于第X個(gè)句子,如果是 Sentence Y is false;
則這個(gè)句子為真的時(shí)候, X ->Y '連邊;
當(dāng)這個(gè)句子為假的時(shí)候,X ' -> Y連邊;
然后求一次強(qiáng)連通,如果最后有某個(gè)點(diǎn)X和X ' 在同一個(gè)連通圖中,說(shuō)明邏輯錯(cuò)誤,說(shuō)明必然存在不合法的情況,否則對(duì)于每個(gè)連通分量,求出為真的點(diǎn)的個(gè)數(shù)和為假的點(diǎn)的個(gè)數(shù),然后將他們之中的大者累加,最后答案除2就是最大的可能為真的句子(除2的原因是因?yàn)檎婕偈菍?duì)稱的)。
C.Will Indiana Jones Get There?
PKU 1292 http://poj.org/problem?id=1292
題意:營(yíng)救公主,營(yíng)救路線要么繞著墻走,要么走兩面墻的最短距離(這種情況下需要在兩面墻之間搭一塊木板,并且可以反復(fù)使用)。問(wèn)營(yíng)救過(guò)程中木板的最短長(zhǎng)度。
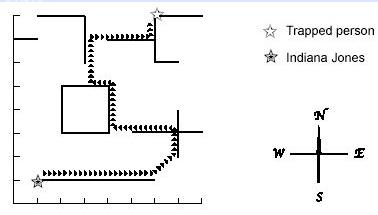
圖C-1
題解:線段距離 + 二分答案
因?yàn)槟景蹇梢苑磸?fù)使用,所以我們可以假設(shè)如果木板越長(zhǎng),能夠營(yíng)救公主的概率就越大,反之則越小,所以問(wèn)題就是求滿足兩點(diǎn)可達(dá)的最小木板長(zhǎng)度,可以二分枚舉這個(gè)長(zhǎng)度T,如果兩面墻的最短距離大于這個(gè)T,表明兩面墻不可達(dá),將墻抽象成點(diǎn),兩面墻之間的最短距離可以通過(guò)線段和線段的最短距離預(yù)處理出來(lái),然后每次二分答案后通過(guò)一次搜索就可以找出起點(diǎn)和終點(diǎn)是否可達(dá),復(fù)雜度為O(n^2)即計(jì)算兩線段距離時(shí)候的復(fù)雜度。
D. Duty Free Shop
PKU 1293 http://poj.org/problem?id=1293
題意:給定M(M <= 1000)個(gè)白巧克力和L(L<= 1000)個(gè)黑巧克力,然后給定N(N <= M + L)個(gè)容量為Ci的盒子,問(wèn)能否找到一種方案,使得某些盒子放滿白巧克力,剩下的盒子放滿黑巧克力。
題解:背包問(wèn)題。
由于需要將每個(gè)盒子都放滿,于是可以利用一維背包的求法將Ci的所有小于等于M的可行組合求出來(lái),找到最大的M ' <= M,并且M ' 能夠通過(guò)某種方式被組合出來(lái),那么所有盒子的容量Sum 減去 M ' 的差小于等于L的話,必定能將剩下的盒子填滿黑巧克力,否則無(wú)解。
這題需要記錄前驅(qū),并且注意M = 0 以及 L = 0 的情況(主要是在輸入的時(shí)候判斷退出條件,M+L==0退出而并非 (M&&L) == 0)。
E.Not Too Convex Hull
PKU 1294 http://poj.org/problem?id=1294
題意:給定N(N<=101)個(gè)點(diǎn)(沒(méi)有三點(diǎn)共線的情況),要求用B(B<=50)根皮條將這N個(gè)點(diǎn)圈成B個(gè)部分,每個(gè)部分為一個(gè)凸多邊形,并且所有凸多邊形公用一個(gè)點(diǎn)(這個(gè)點(diǎn)會(huì)給出),求眾多方案中滿足所有多邊形面積和最小的方案。圖E-1表示用兩根皮條圈住19個(gè)點(diǎn)的情況(原點(diǎn)共用了兩次)。
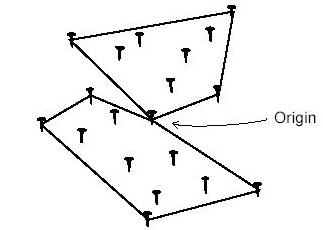
圖E-1
題解:環(huán)形動(dòng)態(tài)規(guī)劃。
首先將所有點(diǎn)按照給定的原點(diǎn)進(jìn)行極坐標(biāo)排序,那么第1個(gè)點(diǎn)到第N個(gè)點(diǎn)必定是按照極坐標(biāo)嚴(yán)格逆時(shí)針排布的(因?yàn)闆](méi)有三點(diǎn)共線),用DP[i][b]表示第i個(gè)點(diǎn)到第N個(gè)點(diǎn)經(jīng)過(guò)b次分割后分割完的凸多邊形的面積總和最小值,那么:
DP[i][b] =min{ area[i][k] +DP[k+1][b-1] (i < k < N) }; 特殊的,DP[0][0] = 0;
area[i][j] 表示極坐標(biāo)在第i個(gè)點(diǎn)和第j個(gè)點(diǎn)之間的所有點(diǎn)(包含這兩個(gè)點(diǎn))加上原點(diǎn)組成的凸包的面積,可以通過(guò)初始化預(yù)處理出來(lái);
由于點(diǎn)是極坐標(biāo)排列的,也就是第一個(gè)點(diǎn)不一定是凸包邊上的點(diǎn)(有可能是第N-1個(gè)點(diǎn)到第2個(gè)點(diǎn)組成的凸包達(dá)到整體最優(yōu)),所以需要做N次DP,可以將所有點(diǎn)復(fù)制一份,枚舉起點(diǎn)i ( 1 <= i <= N),終點(diǎn)即i+N, 然后分別做一次DP取最小值。
時(shí)間復(fù)雜度O(N^2 * B)。
F.I hate SPAM, but some people love it
PKU 1295 http://poj.org/problem?id=1295
題意:N(N<=20)個(gè)人互發(fā)郵件,某個(gè)人收到郵件后一定會(huì)回復(fù)給他所有的好友,回復(fù)的數(shù)量決定他的稱號(hào),按順序給定首先發(fā)起郵件的人,要求按順序輸出所有人得到的稱號(hào)。
題解:深搜枚舉。
數(shù)據(jù)量很小,對(duì)于給定的初始者作為起點(diǎn)進(jìn)行遍歷,每個(gè)人只訪問(wèn)一次,訪問(wèn)到的時(shí)候根據(jù)他的朋友數(shù)量計(jì)算他的稱號(hào)即可。
G.Noise Effect
PKU 1296 http://poj.org/problem?id=1296
題意:給定兩個(gè)正方形矩陣,求他們的最大相似度,相似度的定義為矩陣元素對(duì)應(yīng)位差值小于等于100的個(gè)數(shù)占所有矩陣元素的百分比(可以進(jìn)行旋轉(zhuǎn)和翻轉(zhuǎn))。
題解:模擬題。
每個(gè)矩陣可以進(jìn)行四次旋轉(zhuǎn),每次旋轉(zhuǎn)可以有水平翻轉(zhuǎn)、豎直翻轉(zhuǎn)、水平豎直翻轉(zhuǎn)、保持原樣四種狀態(tài),一共十六種情況(實(shí)際小于16種,因?yàn)橛行顟B(tài)經(jīng)過(guò)翻轉(zhuǎn)和旋轉(zhuǎn)之后是一樣的),對(duì)每種情況模擬計(jì)算相似度取最大值即可。
H.Supermarket
PKU 1297 http://poj.org/problem?id=1297
題意:約翰需要買M(M<=100)件物品,超級(jí)市場(chǎng)上的物品都排成一排,一共N(N<=100000)件物品,他從左向右開始選物品,但是為了不麻煩,不想走回頭路,而且第i個(gè)物品買的條件是,前i-1個(gè)物品必須已經(jīng)買了,但是每個(gè)物品在超級(jí)市場(chǎng)中的價(jià)格不一樣,即使同一個(gè)物品也有不同的價(jià)格,為了花費(fèi)最少,他想要一個(gè)方案使得:
1) 按順序購(gòu)買M個(gè)物品;
2) 總價(jià)值最少,并輸出這個(gè)最小值,如果方案不存在,輸出Impossible。
題解:動(dòng)態(tài)規(guī)劃。
DP[i][j]表示第i個(gè)購(gòu)買列表中的物品和第j個(gè)市場(chǎng)中的物品匹配時(shí)的最小消費(fèi)(1<=i<=M,1<=j<=N);
Min[i][j]表示min{ DP [i][x] x<=j };
a)當(dāng)?shù)?/span>i個(gè)物品和第j個(gè)市場(chǎng)物品編號(hào)相同時(shí),DP[i][j] = Min[i-1][j-1] +cost[j];
b)否則DP[i][j] = inf; 計(jì)算DP數(shù)組同時(shí)更新Min數(shù)組,由于每次的狀態(tài)最多和上一行有關(guān),所以在進(jìn)行狀態(tài)轉(zhuǎn)移的時(shí)候可以采用滾動(dòng)數(shù)組。時(shí)間復(fù)雜度O(NM)。