Asia Hefei Online 2008 解題報告
A. Constellations
PKU 3690 http://poj.org/problem?id=3690
題意:給定N*M(N<=1000, M <= 1000)的01矩陣S,再給定T(T <= 100)個P*Q(P <= 50, Q <= 50)的01矩陣,問P*Q的矩陣中有多少個是S的子矩陣。
題解:位壓縮 + KMP
由于P <= 50,所以我們可以把所有P*Q的矩陣進行二進制位壓縮,將P*Q的矩陣的每一列壓縮成一個64位整數,這樣P*Q的矩陣就變成了一個長度為Q的整數序列,用同樣的方式對N*M的矩陣進行壓縮,總共可以產生(N-P+1)個長度為M的整數序列,剩下的就是進行最多(N-P+1)次KMP匹配了。
KMP相關算法可以參閱:
http://www.shnenglu.com/menjitianya/archive/2014/06/20/207354.html
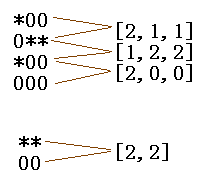
圖1 ‘*’代表二進制的1, ’0’代表二進制的0
B. DNA repair
PKU 3691 http://poj.org/problem?id=3691
題意:給定N(N <= 50)個長度不超過20的模式串,再給定一個長度為M(M <= 1000)的目標串S,求在目標串S上最少改變多少字符,可以使得它不包含任何的模式串(所有串只有ACGT四種字符)。
題解:AC自動機 + 動態規劃
利用模式串建立trie圖,trie圖的每個結點(即下文講到的狀態j)維護三個結構,
Node{
Node *next[4]; // 能夠到達的四個狀態 的結點指針
int id; // 狀態ID,用于到數組下標的映射
int val; // 當前狀態是否是一個非法狀態 (以某些模式串結尾)
}
用DP[i][j]表示長度為i (i <= 1000),狀態為j(j <= 50*20 + 1)的字符串變成目標串S需要改變的最少字符,設初始狀態j = 0,那么DP[0][0] = 0,其他均為無窮大。從長度i到i+1進行狀態轉移,每次轉移枚舉共四個字符(A、C、G、T),如果枚舉到的字符和S對應位置相同則改變值T=1,否則T=0;那么有狀態轉移方程 DP[i][j] = Min{ DP[i-1][ fromstate ] + T, fromstate為所有能夠到達j的狀態 };最后DP[n][j]中的最小值就是答案。
C. Kindergarten
PKU 3692 http://poj.org/problem?id=3692
題意:給定G(G <= 200)個女孩和B(B <= 200)個男孩,以及M(0 <= M <= G*B)條記錄(x, y)表示x號女孩和y號男孩互相認識。并且所有的女孩互相認識,所有的男孩互相認識,求找到最大的一個集合使得所有人都認識。
題解:二分圖最大匹配
一個點集中所有人都認識表示這個點集是個完全圖,該問題就是求原圖的一個最大團(最大完全子圖),可以轉化為求補圖的最大獨立集,而補圖恰好是個二分圖。二分圖的最大獨立集 = 總點數 - 二分圖的最大匹配。于是問題就轉化成了求補圖的最大匹配了。
D. Maximum repetition substring
PKU 3693 http://poj.org/problem?id=3693
題意:給定長度為N(N <= 105)的字符串S,求它的一個最多重復子串(注意:最多重復子串不等于最長重復子串,即ababab和aaaa應該取后者)。
題解:后綴數組 + RMQ
枚舉重復子串的長度L,如果對于某個i,有S[i*L ... N]和S[(i+1)*L ... N]的最長公共前綴大于等于L(這一步可以利用后綴數組求解height數組,然后通過RMQ查詢區間最小值來完成),那么以i*L為首,長度為L的子串至少會重復兩次。
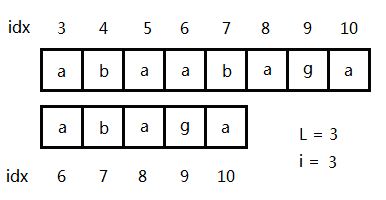
圖2
如圖,L=3,i=3的情況,S[3...10]和S[6...10]的最長公共前綴為3,即S[3...5]和S[6...8]完全匹配,所以S[3...5]重復了兩次。反之,如果最長公共前綴小于L,必定不會重復(因為兩個子串之間出現了斷層)。
推廣到更一般的情況,如果S[i*L ... N]和S[(i+1)*L ... N]的最長公共前綴為T,那么以S[i*L]為首的重復子串的重復次數為T / L + 1,而且我們可以發現如果以S[i*L]為首,長度為L的子串的重復次數大于等于2,那么它一定不會比以S[(i+1)*L]為首的子串的重復次數少,這個是顯然的,比如L為2的時候,ababab一定比abab多重復一次,基于這個性質,我們定義一個new_flag標記,表示是否需要計算接下來匹配到的串(如ababab和abab的情況,前者計算過了,就把new_flag置為false,就不會計算abab的情況了),得出完整算法:
1) 枚舉重復子串的長度L,初始化new_flag標記為true;
2) 枚舉i,計算S[i*L ... N]和S[(i+1)*L ... N]的最長公共前綴T;
a) 如果T < L,new_flag標記為true;
b) 如果T >= L,判斷new_flag是不是為false,如果為false,說明以S[i*L]為首的串和S[(i-1)*L]為首的串的最長公共前綴大于等于T,跳轉到2);否則轉3);
3) 因為S[i*L, (i+1)*L]有重復子串,但是字典序不一定最小,所以還需要枚舉區間 [i-L+1, i+L],看是否存在字典序更小的子串,比較字典序這一步可以直接使用后綴數組計算出來的rank值進行比較。
RMQ相關算法可以參閱:
http://www.shnenglu.com/menjitianya/archive/2014/06/26/207420.html
E. Network
PKU 3694 http://poj.org/problem?id=3694
題意:給定N(N <= 105)個點和M(N-1 <= M <= 2*105)條邊的無向連通圖,進行Q(Q <= 1000)次加邊,每次加入一條邊要求輸出當前圖中有多少條割邊。
題解:無向圖割邊、最近公共祖先
利用tarjan求出原圖的割邊,由于這題數據量比較大,所以用遞歸可能會爆棧,需要棧模擬實現遞歸過程,tarjan計算的時候用parent[u]保存u的父結點,每個結點進出棧各一次,出棧時表示以它為根結點的子樹訪問完畢,然后判斷(u, parent[u])是否為割邊。每次詢問u, v加入后會有多少割邊,其實就是求u和v的到它們的最近公共祖先lca(u, v)的路徑上有多少割邊,由于在進行tarjan計算的時候保存了每個結點的最早訪問時間dfn[u],那么有這么一個性質:dfn[ parent[u] ] < dfn[u],這是顯然的(父結點的訪問先于子結點)。于是當dfn[u] < dfn[v],將parent[v]賦值給v,反之,將parent[u]賦值給u,因為是一棵樹,所以進過反復迭代,一定可以出現u == v 的情況,這時候的u就是原先u和v的最近公共祖先,在迭代的時候判斷路徑上是否存在割邊,路徑上的割邊經過(u, v)這條邊的加入都將成為非割邊,用一個變量保存割邊數目,輸出即可。
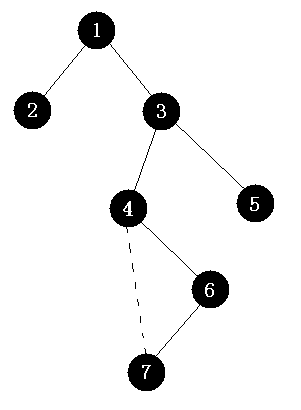
圖3
如圖3,圖中實線表示樹邊,虛線表示原圖中的邊,但是進行tarjan計算的時候7這個結點被(6, 7)這條邊“捷足先登”了,于是(4, 7)成為了一條冗余邊,計算完后這個圖的割邊為(1, 2)、(1,3)、(3, 4)、(3, 5),分別標記bridge[2]、bridge[3]、bridge[4]、bridge[5]為true。
當插入一條邊(7, 5),那么沿著7的祖先路徑和5的祖先路徑最后找到的最近公共祖先為3(路徑為7 -> 6 -> 4 -> 3 和 5 -> 3),(3, 4)、(3, 5)這兩條割邊因為加入了(7, 5)這條邊而變成了普通邊,將標記bridge[4]、bridge[5]置為false。
F. Rectangles
PKU 3695 http://poj.org/problem?id=3695
題意:給定N(N <= 20)個矩形,以及M(M <= 105)次詢問,詢問R(R <= N)個矩形的并。
題解:離散化 + 暴力( 或 容斥原理 )
離散化:由于矩形很少,所以可以將它們的XY坐標分別離散到整點,兩個維度分別離散,點的總數不會超過2N,對于本次詢問,利用前一次詢問的結果進行面積的增減,對每個矩形進行判斷,一共有兩種情況:
1)這個矩形前一次詢問出現,本次詢問不出現,對它的所有離散塊進行自減操作,如果某個離散塊計數減為0,則總面積減去這個離散塊的面積;
2)這個矩形前一次詢問沒出現,本次詢問出現,對它的所有離散塊進行自增操作,如果某個離散塊計數累加后為1,則總面積加上這個離散塊的面積;
容斥原理:對于每個詢問,利用dfs枚舉每個矩形取或不取,取出來的所有矩形作相交操作,所有[奇數個矩形交]的面積和 – 所有[偶數個矩形交]的面積和 就是答案,因為是dfs枚舉,所以在枚舉到某次相交矩形面積為0的時候就不需要再枚舉下去了,算是一個比較強的剪枝。
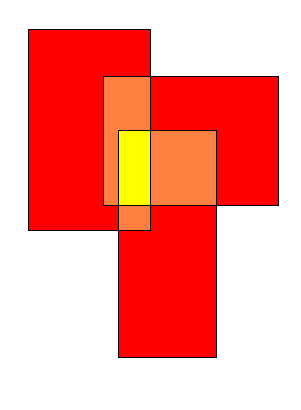
如圖4,紅色區域為被覆蓋了一次的區域,橙色區域為被覆蓋了兩次的區域,黃色區域為被覆蓋了三次的區域,那么先將所有的三個矩形加起來,然后需要減掉重疊的部分,重疊的減掉后發現,重疊的部分多減了,即圖中黃色的部分被多減了一次,需要加回來。所以容斥原理可以概括為:奇數加,偶數減。
圖4
G. The Luckiest number
PKU 3696 http://poj.org/problem?id=3696
題意:給定L(L <= 2*109),求一個最小的數T,滿足T僅由數字’8’組成,并且T是L的倍數。
題解:歐拉定理
首先,長度為N的僅由8組成的數字可以表示為8*(10N-1)/9。
如果它能被L整除,則可以列出等式(1):
8*(10N-1)/9 = KL (其中K為任意正整數) (1)
將等式稍作變形得到等式(2):
(10N-1) = 9KL/8 (2)
由于存在分母,所以我們需要先對分數部分進行約分,得到等式(3):
令A = L/GCD(8, L), B = 8/GCD(8, L)
(10N-1) = 9K*A / B (3)
因為A和B已經互質,所以如果B不為1,為了保證等式右邊仍為整數,K必須能被B整除,而K為任意整數,所以一定能夠找到一個K正好是B的倍數,所以可以在等式兩邊同時模9A,得到(10N-1) mod (9A) = 0,稍作變形,得到等式(4):
(4)
于是需要引入一個定理,即歐拉定理。
歐拉定理的描述為:若n, a為正整數,且n, a互質,則:
圖5
(ψ(n)表示n的歐拉函數,即小于等于n并且和n互素的數的個數)
這樣一來,我們發現只要10和9A互質,只需要求9A的歐拉函數,但是求出來的歐拉函數是不是一定使得N最小呢,并不是,所以還需要枚舉歐拉函數的因子,如果它的某個因子T也滿足(4)的等式,那么T肯定不會比ψ(9A)大,所以T一定更優。
這里9A有可能超過32位整數,所以計算過程中遇到的乘法操作不能直接相乘(兩個超過32位整數的數相乘會超過64位整數),需要用到二分乘法,即利用二進制加法模擬乘法,思想很簡單,就直接給出一段代碼吧。
2
3 //計算 a*b % mod
4 LL Produc_Mod(LL a, LL b, LL mod) {
5 LL sum = 0;
6 while(b) {
7 if(b & 1) sum = (sum + a) % mod;
8 a = (a + a) % mod;
9 b >>= 1;
10 }
11 return sum;
12 }
13
14
15 //計算a^b % mod
16 LL Power(LL a, LL b, LL mod) {
17 LL sum = 1;
18 while(b) {
19 if(b & 1) sum = Produc_Mod(sum, a, mod);
20 a = Produc_Mod(a, a, mod);
21 b >>= 1;
22 }
23 return sum;
24 }
H. USTC campus network
PKU 3697 http://poj.org/problem?id=3697
題意:給定N, M(N <= 104, M <= 106),求N個點的完全圖刪掉M條邊后,和1這個結點相鄰的點的數目。
題解:BFS
利用前向星存邊(這里邊的含義是反的,i和j有邊表示i和j不直接連通)。然后從1開始廣搜,將和1有邊的點hash掉,然后枚舉hash數組中沒有hash掉的點(這些點是和1連通的),如果點沒有被訪問過,標記已訪問,入隊;然后不斷彈出隊列首元素進行相同的處理。
這里可以加入一個小優化,將所有點分組,編號0-9的分為一組,10-19的分為一組,20-29的分為一組,然后用一個計數器來記錄每個組中的點是否被訪問,每次訪問到一個點的時候計數器自增,當某個組的計數器為10的時候表示這個組內所有點都被訪問過了,不需要再進行枚舉了,這樣可以把最壞復雜度控制在 O( N*N/10 ) 以下。
posted on 2014-06-28 19:48 英雄哪里出來 閱讀(2366) 評論(0) 編輯 收藏 引用 所屬分類: 區域賽 解題報告