151 Construct a triangle и§ЈжһҗеҮ дҪ•
152 Making round иҙӘеҝғ
153 Playing With Matches еҚҡејҲ + 规еҫӢ
154 Factorial еҲқзӯүж•°и®ә
155 Cartesian Tree RMQ
156 Strange Graph ӢЖ§жӢүеӣһиө\
157 Patience жЁЎжӢҹжү“иЎЁ
150 Mr. Beetle II
жһҡдӢD
йўҳж„ҸеQҡз»ҷе®ҡдёӨдёӘдәҢҫlҙеқҗж ҮдёҠзҡ„зӮ№(x1, y1)гҖ?/span>(x2, y2)еQҢеқҗж ҮиҢғеӣҙдШ“[-106, 106]гҖӮжұӮд»ҺдёҖдёӘзӮ№(x1, y1)еҲ?/span>(x2, y2)зҡ„зӣҙҫUҝиө\еҫ„дёҠҫlҸиҝҮзҡ„第NдёӘж–№ж јзҡ„е·ҰдёӢи§’еқҗж ҮпјҢж— и§Јиҫ“еҮәno solutionгҖ?/span>
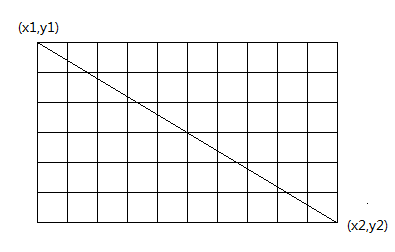
еӣ?
йўҳи§ЈеQҡйҰ–е…ҲпјҢеҰӮжһңдёӨдёӘзӮ№зҡ„xеқҗж ҮзӣёеҗҢжҲ–иҖ?/span>yеқҗж ҮзӣёеҗҢеQҢеҲҷзӣҙжҺҘж— и§ЈеQӣеҗҰеҲҷе°Ҷ(x1, y1)е’?/span>(x2, y2)дёҖиө·еҒҡзӣёеә”зҡ„ег^ҝU»пјҢдҪҝеҫ—(x1, y1)е’?/span>(0, 0)йҮҚеҗҲеQҢж–№дҫҝи®ЎҪҺ—гҖ?/span>
еҰӮжһңx1 < x2еQҢжһҡдё?/span>xеқҗж ҮеұһдәҺ(x1, x2]еQҢеҜ№дәҺжҜҸдёӘеҚ•дҪҚдШ“1зҡ„еҢәй—?/span>[x, x+1]е®ТҺҳ“и®Ўз®—еҮ?/span>yж–№еҗ‘дёҠжңүеӨҡе°‘дёӘж–№ж ы|јҢҫlҹи®ЎеҮә第nдёӘж–№ж ы|јӣеҰӮжһңx1 > x2еQҢжһҡдё?/span>xеқҗж ҮеұһдәҺ(x2, x1]еQҢз”ЁеҗҢж ·зҡ„ж–№жі•иҝӣиЎҢи®ЎҪҺ—гҖ?br />
151 Construct a triangle
и§ЈжһҗеҮ дҪ•
йўҳж„ҸеQҡз»ҷе®ҡдёүи§’еЕһзҡ„дёӨжқЎиҫ№AB = cгҖ?/span> AC = b е’?/span> дёҖжқЎдёӯҫU?/span> AM = m зҡ„й•ҝеәҰпјҢжұӮдёҖдёӘж»Ўӯ‘ПxқЎд»¶зҡ„дёүи§’еҪўзҡ„еқҗж ҮгҖ?/span>
йўҳи§ЈеQҡз”ұдәҺдёүи§’еЕһзҡ„еқҗж ҮеҸҜд»ҘйҡҸж„ҸеҸ–еQҢжүҖд»ҘдШ“дәҶз®ҖеҢ–й—®йўҳпјҢеҸҜд»Ҙһ®?/span>AзӮ№е®ҡеңЁеқҗж ҮеҺҹзӮ№пјҢBзӮ№е®ҡең?/span>xиҪҙжӯЈж–№еҗ‘еQ?/span>CеҲҷеңЁҪW¬дёҖиұЎйҷҗжҲ–иҖ…第дәҢиұЎйҷҗпјӣ
еҒҮи®ҫAеңЁеҺҹзӮ?/span>(0, 0)
Bең?/span>x+иҪҙдёҠеQҢеҲҷжң?/span>BзӮ№еқҗж ?/span>(c, 0)
еҒҮи®ҫCзӮ№еқҗж ҮдШ“(x, y), дёӯзәҝеқҗж Үдё?/span> (B + C) / 2еQҢеҚі ( (x+c)/2, y/2 )
е·ІзҹҘAMи·қзҰ»m е’?/span>ACи·қзҰ»bеQҢеҲҷжңүпјҡ
x2 + y2 = b2 (1)
((x+c)/2)2 + (y/2)2 = m2 (2)
еҗҲеЖҲ(1) (2)еQҢеҲҷжң?/span>
-2cx - c2 = b2 - 4 * m2 (3)
x = (4*m2 -b2 - c2)/2/c; (4)
y2 = b2 - x2; (5)
ж ТҺҚ®(5)еQҢеҸҜд»ҘжҺЁеҮ?/span> y2 = b2 - x2 = b2 - ((4*m2 -b2 - c2)/2/c ) 2 =>[ (b+c) 2 - (2m)2 ] * [ - (b-c)2 + (2m)2 ] > 0
b+c > 2m тq¶дё” 2m > fabs(b-c)ж—?/span>yжүҚжңүи§?/span>еQ?/font>жүҖд»ҘеҪ“ 2*m > (b+c) жҲ–иҖ?/span>2*m < fabs(b-c) дёәж— и§Јзҡ„жғ…еҶөгҖ?/span>
иҖҢжҲ‘们еҒҮи®?/span>CеңЁз¬¬дёҖиұЎйҷҗжҲ–иҖ…第дәҢиұЎйҷҗпјҢжүҖд»?/span>y>0еQҢдәҺжҳ?/span>(x, y)еҸҜйҖҡиҝҮ(4) (5)жұӮеҫ—гҖ?/span>
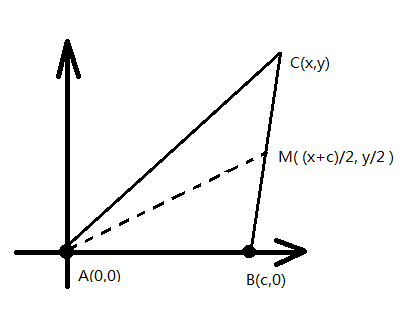
еӣ?/span>2
152 Making round
иҙӘеҝғ
йўҳж„ҸеQҡз»ҷе®?/span>N(N <= 10000)дёӘж•°еQҢжұӮжҜҸдёӘж•°еңЁжүҖжңүж•°дёӯжүҖеҚ зҷҫеҲҶжҜ”еQҢиҰҒжұӮиҫ“еҮәзҡ„ж•оC№Ӣе’ҢдШ“100еQҢжҜҸдёӘж•°еҸҜд»ҘҳqӣиЎҢдёҠдёӢеҸ–ж•ҙгҖӮеҰӮеQҡз»ҷе®ҡдёүдёӘж•°3 3 3еQҢйӮЈд№Ҳиҫ“еҮЮZШ“ 34 33 33гҖ?/span>34дёәеҗ‘дёҠеҸ–ж•ҙзҡ„ҫl“жһңеQ?/span>33дёәеҗ‘дёӢеҸ–ж•ҙзҡ„ҫl“жһңгҖ?/span>
йўҳи§ЈеQ?/span>
1еQүйҰ–е…ҲжұӮеҫ—жүҖжңүж•°д№Ӣе’ҢSеQҢе°ҶжҜҸдёӘж•?/span>a[i]йҷӨдёҠSеҫ—еҲ°е•?/span>B[i]е’ҢдҪҷж•?/span>M[i]гҖ?/span>
2еQүеҰӮжһңдҪҷж•оCШ“0иЎЁзӨәдёәж•ҙйҷӨпјҢдёҚиғҪҳqӣиЎҢдёҠдёӢеҸ–ж•ҙгҖ?/span>еҰӮжһңдҪҷж•°дёҚдШ“0еQҢиҜҙжҳҺе®ғжң?/span> +1 жҲ–иҖ?/span> +0 зҡ„жңәдјҡгҖ?/span> еQҲеӣ дёәйўҳзӣ®иҜҙеҸҜд»ҘдёҠеҸ–ж•Я_јҢд№ҹеҸҜд»ҘдёӢеҸ–ж•ҙеQ?/span>
3) и®°еҪ•дёӢжүҖжңүдҪҷж•оCёҚдёәйӣ¶зҡ„дёӘж•?/span>TгҖ?/span>
4еQүе°ҶжүҖжңүж•°зҡ„е•Ҷд№Ӣе’ҢSum{B[i]} е’?/span> дҪҷж•°дёҚдШ“йӣ¶зҡ„ж•°зҡ„дёӘж•°T зӣёеҠ еQҢеҰӮжһңе°Ҹдә?/span>100еQҢеҲҷиЎЁжҳҺеҝ…е®ҡж— и§ЈгҖ?/span>еҗҰеҲҷжү«жҸҸж•°з»„еQҢе°Ҷ X = 100-Sum{B[i]}-T зҡ„еҖјеҲҶӢz„Ў»ҷжҜҸдёӘдёҚиғҪж•ҙйҷӨзҡ„ж•°еҚӣ_ҸҜеQҲжҜҸдёӘж•°еҸӘеҸҜеҲҶжҙҫ1еQүгҖ?/span>
153 Playing with matches
еҚҡејҲ
йўҳж„ҸеQҡз»ҷе®?/span>Nж №зҒ«жҹ?/span>(N <= 109)еQҢжҜҸӢЖЎеҸҜд»Ҙд»ҺҳqҷдәӣзҒ«жҹҙдёӯеҸ–1,P1,P2,...,Pm (2<=Pi<=9, 0<=m<=8)ж №пјҢдёӨдқhеҲҶеҲ«иҪ®ж¬ЎҳqӣиЎҢжӢ‘ЦҸ–еQҢеЖҲдё”жҖАLҳҜжҢүз…§жңҖдјҳзӯ–з•ҘеҺ»еҸ–пјҢжңҖеҗҺеҸ–е®ҢзҒ«жҹҙзҡ„дәЮZШ“иҫ“зҡ„дәәпјҢй—®еҪ“еүҚзҠ¶жҖҒжҳҜеҗҰжҳҜдёҖдёӘеҝ…иғңзҠ¶жҖҒгҖ?/span>
йўҳи§ЈеQҡз»Ҹе…ёеҚҡејҲпјҢеҜ№дәҺҫlҷе®ҡзҠ¶жҖ?/span>XеQ?/span>
1) еҰӮжһңжҢүз…§жүҖжңүж–№ејҸеҸ–еQҢжңҖеҗҺйғҪеҸӘиғҪи®©еҜ№жүӢеҲ°иҫ‘Цҝ…иғңзҠ¶жҖҒпјҢйӮЈд№ҲXдёәеҝ…иҙҘзҠ¶жҖҒпјӣ
2) еҰӮжһңеҜ№дәҺжҹҗз§ҚеҸ–жі•еQҢеҸҜд»Ҙи®©еҜТҺүӢиҫ‘ЦҲ°еҝ…иУ|зҠ¶жҖҒпјҢйӮЈд№ҲXдёәеҝ…иғңзҠ¶жҖҒпјӣ
3) жҳ„Ў„¶еQ?/span>0дёәеҝ…иғңжҖҒпјҢ1дёәеҝ…иҙҘжҖҒпјҢ2дёәеҝ…иғңжҖҒгҖ?/span>
ж ТҺҚ®д»ҘдёҠзҡ„жҖ§иҙЁеQҢеҸҜд»ҘйҖҡиҝҮйҖ’жҺЁеQҢе°ҶзҒ«жҹҙж ТҺ•°јӢ®е®ҡзҡ„жғ…еҶөдёӢеQҢе°ҶжүҖжңүзҠ¶жҖҒз®—еҮәжқҘеQҢдҪҶжҳҜз”ұдә?/span>N <= 109еQҢж•°жҚ®йҮҸеӨӘеӨ§еQҢдҪҶжҳҜжҲ‘们注ж„ҸеҲ°жҜҸдёӘPiеҫҲе°ҸеQҢжңҖеӨ§еҖйg№ҹеҸӘжңү9еQҢжҹҗдәӣеӨ§зҠ¶жҖҒжҳҜйҖҡиҝҮһ®ҸзҠ¶жҖҒз®—еҮәжқҘзҡ„пјҢжүҖд»Ҙеҝ…然еӯҳеңЁеу@зҺҜгҖ?/span>
дәҺжҳҜй—®йўҳһ®Юpқ{еҢ–жҲҗдәҶжұӮдёҖе ҶеәҸеҲ—зҡ„еҫӘзҺҜиҠӮпјҢеҸҜд»Ҙе…Ҳйў„еӨ„зҗҶһ®?/span>5000еQҲиғцеӨҹеӨ§һ®ЮpЎҢеQүд»ҘеҶ…зҡ„зҠ¶жҖҒз”Ёи®°еҝҶеҢ–жҗңзҙўз®—еҮәжқҘеQҢеҜ№дәҺжҜҸдёӘзҠ¶жҖҒеҖы|јҢз”?/span>0иЎЁзӨәеҝ…иғңеQ?/span>1иЎЁзӨәеҝ…иУ|гҖӮжһҡдё‘Цу@зҺҜиҠӮзҡ„й•ҝеә?/span>lenеQҢ然еҗҺжЈҖӢ№ӢжҳҜеҗҰдёҖдёӘеҗҲжі•зҡ„еҫӘзҺҜиҠӮгҖӮжңҖеҗ?/span>Nзҡ„зҠ¶жҖҒеҖје°ұжҳ?/span>N % lenзҡ„зҠ¶жҖҒеҖ№{Җ?/span>
154 Factorial
дәҢеҲҶҫlҹи®Ў + еҲқзӯүж•°и®ә
йўҳж„ҸеQҡз»ҷе®ҡдёҖдёӘж•°NеQҢжұӮдёҖдёӘжңҖһ®Ҹзҡ„ж•?/span>KеQҢдӢЙеҫ?/span>K!жң«е°ҫжӯЈеҘҪжң?/span>Nдё?/span>0гҖ?/span>
йўҳи§ЈеQҡеӣ дё?/span>K!дёӯзҡ„иҙЁеӣ еӯҗдёӯ5зҡ„дёӘж•°жҳҺжҳҫжҜ”2зҡ„дёӘж•°е°‘еQҢжүҖд»ҘжұӮжң«е°ҫжңүеӨҡһ®‘дёӘ0еQҢе…¶е®һе°ұжҳҜжұӮK!дёӯжңүеӨҡе°‘дёӘиҙЁеӣ еӯҗ5гҖӮйӮЈд№ҲиҝҷдәӣиҙЁеӣ еӯҗдёҖе®ҡеҮәзҺ°еңЁ 5гҖ?/span>10гҖ?/span>15гҖ?/span>25гҖ?/span>30гҖ?/span>35гҖ?/span>... KдёӯпјҢеҜ№дәҺ K!еQҢе°ҶжүҖжңүзҡ„5зҡ„еҖҚж•°жҸҗеҮәжқҘпјҢеү©дёӢйғЁеҲҶдё?/span>TеQҢеҲҷжңүпјҡ
K! = 1*2*3*4*5*...(K-1)*K = 5 * 10 * 15 * ... * (1*2*3*4*6*7*8*9*11*12*13*14*16*...K) = 5*10*15*...* T = 5* (1*2*3...) * T = 5 * T * K'! еQ?/span> жҲ‘们еҸ‘зҺ°5*Tдё?/span>5зҡ„иҙЁеӣ еӯҗдёӘж•°дё?/span>TдёӘпјҢK'! дёӯзҡ„5зҡ„дёӘж•°еҲҷеҸҜд»ҘиҪ¬еҢ–жҲҗеӯҗй—®йўҳжұӮи§ЈеQҢиҝҷж ·е°ұеҸҳжҲҗдәҶдёҖдёӘйҖ’еҪ’жұӮи§ЈKдёӯиҙЁеӣ еӯҗдё?/span>5зҡ„дёӘж•?/span>Sзҡ„й—®йўҳпјҢйҖ’еҪ’ж–№зЁӢдё?/span> S[ K ] = K/5 + S[K/5] ( K > 0 ) еҪ?/span>K = 0ж—¶иҝ”еӣ?/span>0еQҢеҚійҖ’еҪ’еҮәеҸЈгҖ?/span>
йӮЈд№Ҳһ®ұеҸҜд»ҘдәҢеҲҶжһҡдёҫдёҖдё?/span>KеQҢ然еҗҺйҖҡиҝҮдёҠйқўзҡ„йҖ’еҪ’жұӮи§ЈKдё?/span>5ҳqҷдёӘиҙЁеӣ еӯҗзҡ„дёӘж•°еQҢ然еҗҺе’ҢNжҜ”иҫғеQҢеҰӮжһңжүҫдёҚеҲ°дёҖдё?/span>KеQҢдӢЙеҫ—е®ғзҡ?/span>5иҙЁеӣ еӯҗзҡ„дёӘж•°дё?/span>NеҲҷж— и§ЈпјҢеҗҰеҲҷжүҫдёҖдёӘжңҖһ®Ҹзҡ„гҖ?/span>
155 Cartesian Tree
RMQ(or ZigZag)
йўҳж„ҸеQҡз»ҷе®?/span>N(N <= 50000)дёӘж•ҙж•°еҜ№(key, a)еQҢиҰҒжұӮе°Ҷ他们ҫl„з»ҮжҲҗдёҖӢӮү| ‘дәҢеҸүж ‘пјҢтq¶дё”еҜ№дәҺж ‘зҡ„д»АL„ҸдёҖдёӘз»“зӮ№пјҢж»ЎиғцеҰӮдёӢдёӨдёӘжҖ§иҙЁеQ?/span>
1) еҪ“еүҚҫl“зӮ№зҡ?/span>aеҖјеӨ§дәҺе®ғзҲ¶иҠӮзӮ№зҡ„aеҖ?/span>(һ®ҸйЎ¶е Ҷзҡ„жҖ§иҙЁ)еQ?/span>
2) еҪ“еүҚҫl“зӮ№зҡ?/span>keyеҖјеӨ§дәҺе·Ұеӯҗж ‘зҡ?/span>keyеҖы|јҢтq¶дё”һ®ҸдәҺеҸӣ_ӯҗж ‘зҡ„keyеҖ?/span>(жҺ’еәҸдәҢеҸүж ‘зҡ„жҖ§иҙЁ)еQ?/span>
йўҳзӣ®дҝқиҜҒжүҖжңүзҡ„keyеҖје’ҢaеҖјйғҪдёҚеҗҢгҖ?/span>
йўҳи§ЈеQҡйҰ–е…Ҳе°ҶжүҖжңүж•ҙж•°еҜ№жҢ?/span>keyеҖјйҖ’еўһжҺ’еәҸеQҢиҝҷж дhҲ‘们еҸӘйңҖиҰҒеҜ№ж•°з»„ҳqӣиЎҢеҲҮеҲҶеQҢеҰӮжһң第tдёӘз»“зӮ№дҪңдёәж №ҫl“зӮ№еQҢйӮЈд№?/span>[1, t-1]еҝ…е®ҡжҳҜе®ғзҡ„е·Ұеӯҗж ‘йӣҶеҗҲеQ?/span>[t+1, N]еҝ…е®ҡжҳҜе®ғзҡ„еҸіеӯҗж ‘йӣҶеҗҲеQҢиҝҷж ·е°ұиғҪеӨҹдҝқиҜҒҪW¬дәҢдёӘжқЎд»УһјҢиҖҢ第дёҖдёӘжқЎд»үҷңҖиҰҒж»Ўӯ‘ізҲ¶иҠӮзӮ№зҡ?/span>aеҖје°ҸдәҺе·ҰеҸӣ_ӯҗж ‘зҡ„aеҖы|јҢжүҖд»Ҙ第tдёӘз»“зӮ№еҝ…е®ҡжҳҜжүҖжңүж•°дё?/span>aеҖјжңҖһ®Ҹзҡ„еQҢдәҺжҳҜеҸҜд»Ҙ规ҫUҰеҮәдёҖдёӘйҖ’еҪ’ҪҺ—жі•еQҢеҜ№дәҺеҪ“еүҚеҢәй—?/span>[l, r]еQҢжүҫеҲ°еҢәй—ҙеҶ…aеҖјжңҖһ®Ҹзҡ„дҪңдШ“ж №з»“зӮ№пјҢ然еҗҺһ®Ҷе®ғе·Ұиҫ№зҡ„еҢәй—ҙе’ҢеҸҢҷҫ№зҡ„еҢәй—ҙиҝӣиЎҢзӣёеҗҢзҡ„йҖ’еҪ’ҳqҗз®—гҖӮеҲқе§ӢеҢәй—ҙдШ“[1, N]еQҢеҪ“[l, r]ж»Ўиғц l > rеҚідШ“йҖ’еҪ’еҮәеҸЈгҖӮжұӮеҢәй—ҙжңҖһ®ҸеҖјеҸҜд»ҘйҮҮз”?/span>RMQгҖ?/span>жҖИқҡ„ж—үҷ—ҙеӨҚжқӮеәҰдШ“жҺ’еәҸзҡ„ж—¶й—ҙеӨҚжқӮеәҰO(N log N)гҖ?/span>
RMQ иө„ж–ҷеҸӮйҳ… http://www.shnenglu.com/menjitianya/archive/2014/06/26/207420.html
156 Strange Graph
ӢЖ§жӢүеӣһиө\
йўҳж„ҸеQҡз»ҷе®ҡдёҖдё?/span>N(N <= 10000)дёӘзӮ№зҡ„иҝһйҖҡеӣҫеQҢиҝҷдёӘеӣҫж»Ўиғцд»ҘдёӢжҖ§иҙЁеQ?br /> 1) жҜҸдёӘҷе¶зӮ№vзҡ„еәҰж•°йғҪеӨ§дәҺҪ{үдәҺ2еQ?br /> 2) еҰӮжһңҷе¶зӮ№vзҡ„еәҰж•°зӯүдә?/span>2еQҢйӮЈд№Ҳе®ғҳqһжҺҘзҡ„дёӨдёӘйЎ¶зӮ№дёҚзӣ”RӮ»еQ?br /> 3) еҰӮжһңҷе¶зӮ№vзҡ„еәҰж•°еӨ§дә?/span>2еQҢйӮЈд№Ҳе’Ңvзӣ”RӮ»зҡ„зӮ№uж»Ўиғцд»ҘдёӢжқЎдҡgд№ӢдёҖеQ?br /> a) uзҡ„еәҰж•°зӯүдә?/span>2еQ?br /> b) д»ЦMҪ•е’?/span>vзӣ”RӮ»зҡ„зӮ№(йҷӨдәҶu)дёӯйғҪдёӨдёӨзӣ”RӮ»еQ?/span>
жұӮиҝҷдёӘеӣҫзҡ„дёҖдёӘе“ҲеҜҶе°”ҷеҝеӣһи·?/span>(ҫlҸиҝҮжҜҸдёӘҷе¶зӮ№дёҖӢЖЎзҡ„еӣһиө\)гҖ?/span>
йўҳи§ЈеQҡйҰ–е…Ҳе°ҶжүҖжңүеәҰж•оCШ“2зҡ„зӮ№ҳqӣиЎҢж Үи®°еQҢйӮЈд№Ҳд»ҺҳqҷдёӘеӣ„Ўҡ„е®ҡд№үдёӯеҸҜзҹҘпјҢжңӘж Үи®°зҡ„зӮ№еҝ…е®ҡжҳҜеңЁдёҖдёӘе®Ңе…Ёеӯҗеӣҫдёӯзҡ„пјҢһ®ҶеӣҫдёӯжүҖжңүе®Ңе…Ёеӯҗеӣҫдёӯзҡ„зӮ№ҫ~©жҲҗдёҖдёӘзӮ№еQҢеҜ№ҫ~©е®ҢзӮ№зҡ„еӣ„Ў»ҹи®ЎеәҰж•ҺНјҢеҰӮжһңжүҖжңүзҡ„зӮ№зҡ„еәҰж•°йғҪдШ“еҒ¶ж•°еQҢйӮЈд№Ҳеҝ…е®ҡеӯҳеңЁдёҖдёӘ欧жӢүеӣһи·ҜпјҢжұӮеҮәӢЖ§жӢүеӣһиө\еҗҺеҶҚжӢҶзӮ№иҪ¬жҚўжҲҗе“ҲеҜҶе°”ҷеҝеӣһи·ҜпјӣеҗҰеҲҷеQҢ欧жӢүеӣһи·ҜдёҚеӯҳеңЁеQҢе“ҲеҜҶе°”ҷеҝеӣһи·Ҝд№ҹһ®ЧғёҚеӯҳеңЁгҖ?/span>
157 Patience
жү“иЎЁйў?br /> йўҳж„ҸеQҡз»ҷе®?/span>N(1 <= N <= 13)еQҢиЎЁҪC?/span>(1 2 3 ... N ҪI?/span>)ҳq?/span>N+1дёӘдҪҚҫ|®пјҢе…¶дёӯNдёӘдҪҚҫ|®йҡҸжңәжҺ’ж”„ЎқҖ1-Nдёӯзҡ„жҹҗдёҖеј зүҢеQҢжҜҸӢЖЎеҸҜд»ҘеңЁ“ҪI?#8221;е·Ұиҫ№зҡ„дҪҚҫ|®жүҫеҲоCёҖеј зүҢKеQҢ然еҗҺе°ҶK+1ҳqҷеј зүҢж”ҫең?#8220;ҪI?#8221;зҡ„дҪҚҫ|®дёҠеQҢй—®е“ӘдәӣеҲқе§ӢзҠ¶жҖҒеҸҜд»ҘеҲ°иҫҫдёҖдёӘзҠ¶жҖҒдӢЙеҫ—еүҚNдёӘж јеӯҗзҡ„зүҢжңүеәҸжҺ’еҲ—пјҲҪW?/span>N+1дёӘдҪҚҫ|®з•ҷҪIәпјүгҖ?br /> йўҳи§ЈеQҡд»Һ(1 2 3 ... N ҪI?/span>)ҳqҷдёӘзҠ¶жҖҒи“vеQҢеҸҚеҗ‘жЁЎжӢҹпјҢиғҪеӨҹеҲ°иҫҫзҡ„зҠ¶жҖҒйғҪжҳҜеҸҜиҫ„ЎҠ¶жҖҒпјҢҫlҹи®ЎжүҖжңүеҸҜиҫ„ЎҠ¶жҖҒзҡ„дёӘж•°еQ?/span>Nзҡ„жңҖеӨ§еҖйgШ“13еQҢж—¶й—ҙдёҠдёҚе…Ғи®ёеҸҜд»Ҙе®ўжҲпL«Ҝи®Ўз®—еҮәеҖјз„¶еҗҺжү“иЎЁпјҒ
158 Commuter Train
дәҢеҲҶжһҡдӢD
йўҳж„ҸеQҡиһRз«ҷй•ҝеәҰдШ“L(L <= 5000)еQҢз»ҷе®?/span>NеQ?/span>N<= 300еQүдёӘд№ҳе®ўеңЁиһRз«ҷзҡ„дҪҚзҪ®еQҢд»ҘеҸҠдёҖиҫҶе…¬дәӨиһRзҡ?/span>MеQ?/span>M <= 300еQүдёӘиҪҰй—Ёјӣ»иһRеӨҙзҡ„дҪҚзҪ®еQҢд№ҳе®ўдёҖе®ҡдјҡйҖүжӢ©јӣ»иҮӘе·ұжңҖҳq‘зҡ„иҪҰй—Ёҳqӣе…ҘеQҢй—®ҳqҷиҫҶиҪҰиҰҒеҒңеңЁе“ӘйҮҢеҸҜд»ҘдҪҝеҫ—жүҖжңүдқhҳqӣе…ҘиҪҰй—ЁйңҖиҰҒиө°зҡ„и·қјӣАLҖХd’ҢжңҖеӨ§пјҢеҘҪеҸҳжҖҒзҡ„жғПxі•гҖ?/span>
йўҳи§ЈеQҡеҸӘиҰҒжһҡдёҫиһRйңҖиҰҒеҒңйқ зҡ„дҪҚзҪ®еQҢ然еҗҺжһҡдёҫжҜҸдёӘдқhеҲ°иҫҫзҡ„йӮЈдёӘиһRй—ЁиҠұиҙ№зҡ„и·қзҰ»жҖХd’ҢеQҢеҸ–жңҖеӨ§еҖје°ұжҳҜзӯ”жЎҲгҖ?/span>
ҳqҷйҮҢеҜ№дәҺжҹҗдёӘдәәйңҖиҰҒеҺ»е“ӘдёӘиҪҰй—ЁеҸҜд»ҘйҮҮз”ЁдәҢеҲҶжһҡдӢDеQҢеӣ дёшҷһRй—ЁжҳҜжңүеәҸзҡ„пјҢеҸӘиҰҒдәҢеҲҶжү‘ЦҲ°јӣХd®ғжңҖҳq‘зҡ„е·ҰиһRй—ЁпјҢйӮЈд№ҲдёӢдёҖдёӘе°ұжҳҜжңҖҳq‘зҡ„еҸҢҷһRй—ЁпјҲйңҖиҰҒиҖғиҷ‘иҫ№з•ҢеQҢжңҖе·Ұе’ҢжңҖеҸізҡ„жғ…еҶөйғҪеҸӘжңүдёҖдёӘиһRй—ЁпјүеQҢ然еҗҺеҸ–е·ҰгҖҒеҸіиҪҰй—Ёзҡ„и·қјӣХd°ҸиҖ…гҖ?/span>д»”з»ҶжғідёҖдёӢпјҢжңҖеӨ§еҖйgёҚдёҖе®ҡеҮәзҺ°еңЁж•ҙзӮ№дёҠпјҢд№ҹжңүеҸҜиғҪеҮәзҺ°ең?/span>0.5зҡ„дҪҚҫ|®дёҠеQҢжүҖд»ҘеҸҜд»Ҙе°ҶжүҖжңүеқҗж ҮйғҪд№?/span>2еQҢ然еҗҺжңҖеҗҺзӯ”жЎҲеҶҚйҷӨдәҢйҒҝе…Қҫ_‘ЦәҰиҜҜе·®гҖ?/span>
159 Self-Replicating Numbers
ж·ұеәҰдјҳе…ҲжҗңзғҰ
йўҳж„ҸеQ?/span>жұ?/span>N(N <= 2000)дҪ?/span>BҳqӣеҲ¶ж•оCёӯтqПx–№зҡ„жңҖеҗҺеҮ дҪҚзӯүдә?/span>иҜҘж•°жң¬инnзҡ„ж•°зҡ„дёӘж•°гҖ?/span>
йўҳи§ЈеQҡеҲ©з”?/span>dfsд»ҺжңҖеҗҺйқўдёҖдҪ?/span>digitејҖе§Ӣжһҡдё?/span>[0, B)еQҢжЁЎжӢҹзӣёд№ҳеҗҺеҜ№еә”дҪҚзҡ„дҪҷж•°еQҢеҰӮжһңе’ҢиҜҘж•°зҡ„жһҡдёщNӮЈдёҖдҪҚдёҚзӣёз¬ҰеҲҷдёҚҳqӣиЎҢдёӢдёҖжӯҘжҗңзҙўпјҢеҪ“жһҡдё‘ЦҲ°ҪW?/span>NдҪҚе®ҢжҜ•пјҢеҲҷе°Ҷи§ЈдҝқеӯҳпјҢҳqҷйҮҢйңҖиҰҒжіЁж„ҸеҪ“Nдё?/span>1зҡ„ж—¶еҖҷпјҢжңҖй«ҳдҪҚеҸҜд»Ҙдё?/span>0еQҢеҗҰеҲҷжңҖй«ҳдҪҚдё?/span>0зҡ„жғ…еҶөйңҖиҰҒеҺ»жҺүпјҲжңҖй«ҳдҪҚдё?/span>0иҜҙжҳҺе®ғдёҚжҳ?/span>NдҪҚж•°еQ?/span>N>1еQүпјүгҖ?/span>
121 Bridges painting еӣҫи®әеQҡжҹ“иүІй—®йў?/span>
122 The Book еӣҫи®әеQҡе“ҲеҜҶе°”ҷеҝеӣһи·?/strong>
123 The Sum йҖ’жҺЁ
124 Broken Line и®Ўз®—еҮ дҪ•еQҡзәҝҢDөеҲӨдә?a >
125 shtirlits жҗңзғҰеQҡж·ұеәҰдјҳе…Ҳжҗңзҙ?/strong>
126 boxes еҲқзӯүж•°и®ә
127 Telephone directory жҺ’еәҸ
128 Snake жҺ’еәҸ + HASH
129 Inheritance и®Ўз®—еҮ дҪ•еQҡеҮёеҢ?ҫUҝж®өеҲӨдәӨ
120 Archipelago
и®Ўз®—еҮ дҪ•еQҡе°„ҫUҝж—ӢиҪ?br />
йўҳж„ҸеQҡйңҖиҰҒжұӮдёҖдёӘжӯЈеӨҡиҫ№еҪўзҡ„NдёӘзӮ№еQҢдҪҶжҳҜз»ҷеҮәзҡ„еҸӘжңүNе’ҢжҹҗдёӨдёӘзӮ№зҡ„еқҗж ҮгҖ?/span>
йўҳи§ЈеQҡж ёеҝғжҖқжғіжҳҜж №жҚ®з»ҷе®ҡзҡ„йӮЈдёӨдёӘзӮ№зҡ„еқҗж ҮзЎ®е®ҡеӨҡиҫ№еЕһдёӯеҝғзӮ№зҡ„еқҗж ҮеQҢиҝҷж ҜӮҫ№й•ҝд№ҹјӢ®е®ҡдәҶпјҢ然еҗҺеҲ©з”ЁдёӯеҝғзӮ№еҲ°е…¶дёӯдёҖдёӘзӮ№зҡ„е°„ҫUҝзҡ„ж—Ӣиқ{жұӮеҮәжүҖжңүзҡ„зӮ№еқҗж ҮгҖ?/span>
1) жӯЈеӨҡиҫ№еЕһзҡ„дёӯеҝғзӮ№дёҖе®ҡеңЁд»АL„ҸдёӨдёӘҷе¶зӮ№зҡ„иҝһҫUҝзҡ„дёӯеһӮҫUҝдёҠеQҢ然еҗҺж №жҚ®е·ІзҹҘзӮ№зҡ„зӣёеҜ№е…іҫp»пјҢҪҺ—еҮә他们е’ҢдёӯеҝғзӮ№зҡ„еӨ№и§’пјҢеҲ©з”ЁҳqҷдёӨдёӘжқЎд»¶е°ұеҸҜд»ҘжұӮеҮәдёӯеҝғзӮ№зҡ„еқҗж ҮдәҶгҖ?/span>
2) 然еҗҺһ®ұжҳҜиҰҒжұӮжҹҗдёӘзӮ№з»•дёӯеҝғзӮТҺ—ӢиҪ?/span>360/NеәҰеҗҺзҡ„еқҗж ҮдәҶеQҢеҒҡN-1ӢЖЎж—ӢиҪ¬ж“ҚдҪңе°ұиғҪжұӮеҮәжүҖжңүзҡ„ҷе¶зӮ№дәҶгҖӮж—ӢиҪ¬еҸҜд»ҘйҖҡиҝҮи§Јж–№ҪEӢжұӮи§Јпјҡ
д»ӨеҺҹеҚ•дҪҚеҗ‘йҮҸIеQҢж—ӢиҪ?/span>alphaи§’еәҰеҗҺзҡ„еҚ•дҪҚеҗ‘йҮҸIaеQҢе…¶дё?/span>Iе’?/span>alphaе·ІзҹҘеQ?/span>IxжҳҜжҲ‘们йңҖиҰҒжұӮзҡ„гҖӮйӮЈд№Ҳжңүд»ҘдёӢдёӨдёӘж–№зЁӢеQ?/span>
1) I.x * Ia.x + I.y * Ia.y = cos( alpha )
2) Ia.x2 + Ia.y2 = 1
һ®?/span>1)дёӯзҡ„Ia.xз”?/span>Ia.yиЎЁзӨәд»Је…Ҙж–№зЁӢ2)еQҢеҲ©з”ЁдёҖе…ғдәҢӢЖЎжұӮж №е…¬ејҸеҸҜд»ҘжұӮеҫ—дёӨдёӘи§ЈеQҢ然еҗҺз®—еҮ?/span>Ia.xеQҢдҪҶжҳҜи§ЈиӮҜе®ҡеҸӘжңүдёҖдёӘпјҢеҸҜд»Ҙз”ЁеҸүд№ҳе…іҫpАLҺ’йҷӨжҺүеҸҰеӨ–дёҖдёӘи§ЈгҖ?br />
121 Bridges painting
еӣҫи®әеQҡDFSжһ„йҖ?/span>
йўҳж„ҸеQҡеҜ№дәҺдёҖдёӘеӣҫеQҢз»ҷе®ҡе®ғзҡ„иҫ№е’ҢзӮ№еQҢзҺ°еңЁиҰҒжұӮз»ҷиҫТҺҹ“иүФҢјҲй»‘иүІжҲ–иҖ…зҷҪиүФҢјүгҖӮй—®иғҪдёҚиғҪжһ„йҖ дёҖҝUҚжҹ“иүІж–№жі•пјҢдҪҝеҫ—жүҖжңүзҡ„еәҰж•°еӨ§дәҺ1зҡ„зӮ№зҡ„иҫ№йғҪиғҪжңүиҮіһ®‘жңүдёҖжқЎиҫ№дёәй»‘иүҢУҖҒиҮіһ®‘жңүдёҖжқЎиҫ№дёәзҷҪиүҢУҖ?/span>
йўҳи§ЈеQҡйҰ–е…ҲиҖғиҷ‘д»Җд№Ҳжғ…еҶөдёӢжҳҜдёҚеҸҜиғҪжҹ“иүІжҲҗеҠҹзҡ„пјӣеҰӮеӣҫ1жүҖҪCәпјҢеҜ№дәҺдёӢйқўҳqҷдёӘеӣҫпјҢжҜҸдёӘзӮ№зҡ„ҷе¶зӮ№еәҰж•°дё?/span>2еQҢжүҖд»Ҙд»Һд»АL„ҸдёҖжқЎиҫ№ејҖе§Ӣжҹ“иүФҢјҢзӣ”RӮ»иҫ№еҝ…然дШ“зӣёеҸҚиүФҢјҢз”ЧғәҺеӯҳеңЁеҘҮзҺҜеQҢеҜјиҮҙеҝ…然жңүдёҖдёӘзӮ№зҡ„дёӨжқЎиҫ№зҡ„йўңиүІзӣёеҗҢпјҢжҹ“иүІеӨЮpУ|гҖ?/span>
然еҗҺеҶҚжқҘиҖғиҷ‘жҖҺд№Ҳһ®ҶиҝҷдёӘеӣҫжҢҪж•‘еӣһжқҘеQҢе…¶е®һиҝҷдёӘеӣҫеӨЮpУ|зҡ„зӮ№еҸӘжңүдёҖдёӘпјҢеҰӮжһңеңЁйӮЈдёӘзӮ№дёҠеҶҚеҠ дёҖжқЎиҫ№еQҢйӮЈд№Ҳж•ҙдёӘеӣҫиІҢдјјһ®ұеҸҜд»Ҙи®Өдёәжҹ“иүІжҲҗеҠҹдәҶгҖ?/span>
дәҺжҳҜжҲ‘们ҳqӣдёҖжӯҘиҖғиҷ‘жҳҜдёҚжҳҜеәҰж•оCШ“еҘҮж•°зҡ„зӮ№йҖ е°ұдәҶиҝҷдёҖеҲҮпјҡ
еәҰж•° = 1еQҢиҜҘзӮТҺүҖеңЁиҫ№еҸҜд»ҘйҡҸдҫҝжҹ“иүІеQ?/span>
еәҰж•° > 1еQҢиҜҙжҳҺеҝ…然еӯҳеңЁзҺҜеQ?/span>
еҰӮжһңжҳҜеҒ¶ж•°зҺҜеQҢйӮЈд№Ҳз»ҸҳqҮдёҖҫpХdҲ—зҡ„дәӨй”ҷжҹ“иүФҢјҢжңҖеҗҺеҝ…然иғҪеӨҹеңЁиҜҘз»“зӮ№дёҠ收иҺ·дёӨжқЎйўңиүІдёҚдёҖж пLҡ„иҫ№пјӣ
еҰӮжһңжҳҜеҘҮж•°зҺҜеQҢеңЁжҹ“иүІе®ҢжҜ•еҗҺпјҢеҝ…然ҳqҳжңүдёҖжқЎиҫ№жңӘиў«жҹ“иүІеQҲеӣ дёәеәҰж•оCШ“еҘҮж•°еQүпјҢеҸҜд»ҘеӨ§иғҶзҡ„е°Ҷе®ғжҹ“жҲҗдёҚеҗҢзҡ„йўңиүІеQ?/span>
жүҖд»ҘеҜ№дәҺеәҰж•оCШ“еҘҮж•°зҡ„зӮ№еQҢйҮҮз”ЁдәӨй”ҷжҹ“иүФҢјҢдёҖе®ҡеҸҜд»Ҙе°Ҷеӣҫжҹ“иүІжҲҗеҠҹпјӣ
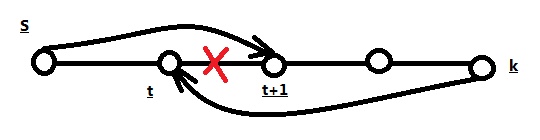
еҰӮеӣҫеQҢеҸҜд»ҘеҜ№дәҺжүҖжңүеҘҮеәҰж•°ҷе¶зӮ№дҪңдШ“ж №иҝӣиЎҢдёҖӢЖ?/span>dfsеQҢжҢүз…§зј–еҸ·йЎәеәҸиҝӣиЎҢж·ұеәҰдјҳе…ҲйҒҚеҺҶпјҢе…ҲйҒҚеҺҶеҲ°зҡ„жҳҜ1еҸшPјҢж Үи®°дёәй»‘иүФҢјҢ然еҗҺһ®Ҷе®ғзҡ„第дёҖдёӘе„ҝеӯҗж Үи®оCШ“зҷҪиүІеQҢйҒҚеҺҶе®ҢжҜ•пјҢһ®Ҷ第дәҢдёӘе„ҝеӯҗж Үи®°дёәй»‘иүФҢјҲдәӨй”ҷжҹ“иүІеQүпјҢеҚПxҜҸӢЖЎжӣҙжҚўз»“зӮ№зҡ„ж—¶еҖҷе°ұһ®ҶйўңиүІеҸ–еҸҚпјҢеҪ“жҲ‘们йҒҚеҺҶеҲ°иҫ?/span>6зҡ„ж—¶еҖҷеҸ‘зҺ?/span>7жҳҜдёҖжқЎеҗҺеҗ‘иҫ№еQҢдәҺжҳҜеӣһеҲоCәҶж №з»“зӮ№пјҢе®ҢжҲҗйҒҚеҺҶгҖ?/span>
еҲ©з”ЁеҗҢж ·ж–ТҺі•еQҢе°ҶжүҖжңүеәҰж•оCШ“еҘҮж•°зҡ„зӮ№ҳqӣиЎҢдёҖӢЖЎйҒҚеҺҶпјҢ然еҗҺеҶҚе°ҶеәҰж•°дёәеҒ¶ж•°зҡ„зӮ№иҝӣиЎҢзӣёеҗҢзҡ„йҒҚеҺҶеQҲеӣ дёәеҸҜиғҪиҝҷдёҚжҳҜдёҖдёӘиҝһйҖҡеӣҫеQҢжүҖд»ҘеҰӮжһңеәҰж•оCШ“еҒ¶ж•°зҡ„зӮ№жүҖеңЁзҡ„еӣщNӣҶеҗҲдёӯжңүеҘҮж•°зҺҜеQҢеҰӮеӣ?/span>1зҡ„жғ…еҶөпјҢйӮЈд№Ҳеҝ…з„¶ж— и§ЈеQүгҖ?/span>
йҒҚеҺҶе®ҢжҜ•еQҢйңҖиҰҒеҜ№жҜҸдёӘзӮ№еҲӨж–ӯжҳҜеҗҰеӯҳеңЁдёҚеҗҲжі•зҡ„йЎ¶зӮ№пјҲиҫТҺ•°еӨ§дәҺ1еQҢеЖҲдё”еҸӘжңүдёҖҝUҚжҹ“иүФҢјүеQҢеҰӮжһңеҗҲжі•пјҢиҜҙжҳҺжүҖжңүиҫ№йғҪиў«жҹ“иүІдәҶпјҢиҫ“еҮәи§ЈеҚіеҸҜгҖ?/span>
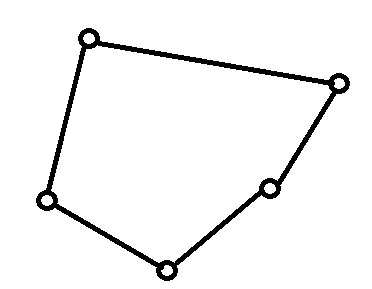
еӣ?/span>1
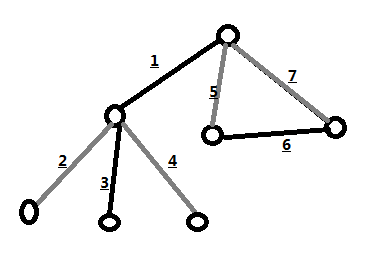
еӣ?/span>2
е“ҲеҜҶһ®”йЎҝеӣһиө\й—®йўҳеQҡOreе®ҡзҗҶ + жһ„йҖ?/span>
йўҳж„ҸеQҡз»ҷе®?/span>N(N <= 1000)дёӘзӮ№ҳqһжҲҗзҡ„еӣҫеQҢжҜҸдёӘзӮ№еәҰж•°еӨ§дәҺҪ{үдәҺ(N+1)/2еQҢжұӮҳqҷдёӘеӣ„Ўҡ„дёҖжқЎе“ҲеҜҶе°”ҷеҝеӣһи·ҜгҖ?/span>
йўҳи§ЈеQ?/span>
1еQүйҰ–е…ҲеҒҮи®‘Ц·ІҫlҸеҫ—еҲоCәҶдёҖдёӘзҺҜRеQ?/span>Rзҡ„йЎ¶зӮ№дёӘж•оCШ“rеQүпјҢйӮЈд№ҲеңЁжңӘйҖүеҲ°зҺҜеҶ…зҡ„зӮ№йӣ?/span>R’дёӯеҝ…然иғҪеӨҹжүҫеҲ°жҹҗдёӘзӮ№kе’ҢзҺҜRдёӯе…¶дёӯдёҖдёӘзӮ№jжңүиҫ№зӣёиҝһеQҢеҒҮи®ҫжІЎжңүиҫ№зӣёиҝһеQҢйӮЈд№ҲзҺҜRе’ҢзҺҜеӨ–зҡ„зӮҡwӣҶR’дә’дёҚҳqһйҖҡпјҢдёЮZёӨдёӘиҝһйҖҡеҲҶйҮҸпјҢе’Ңйўҳж„Ҹзӣёе·ҰпјҲеӣ дШ“жҜҸдёӘзӮ№зҡ„еәҰж•°еӨ§дәҺҪ{үдәҺеQ?/span>N+1еQ?/span>/2еQҢеӣҫи®ЮZ№ҰдёҠжңүиҜҒжҳҺеQҢиҝҷиӮҜе®ҡжҳҜдёҖдёӘиҝһйҖҡеӣҫеQҢж•…дёҚеҶҚзҙҜиҝ°еQүпјҢж•?/span>R’дёӯеҝ…然еӯҳеңЁиҮіһ®‘дёҖдёӘзӮ№kе’?/span>RдёӯзӮ№jзӣёиҝһеQҢдәҺжҳҜе°ҶйӮЈдёӘзӮ?/span>jҳqһжҺҘеҲ?/span>kдёҠпјҢҳqҷж ·һ®ұеҸҳжҲҗдәҶдёҖдёӘй•ҝеәҰдШ“r+1зҡ„й“ҫгҖ?/span>
2еQүиҝҷдёӘй“ҫзҡ„еӨҙдё?/span>sеQҢе°ҫдё?/span>kеQҢй•ҝеәҰдШ“r+1еQҢдёҚж–ӯеңЁеү©дёӢзҡ„зӮ№йӣҶдёӯжү„ЎӮ№ҳqһжҺҘеҲ?/span>sе’?/span>kдёҠпјҢтq¶дё”дёҚж–ӯжӣҙж–°sе’?/span>kеQҲиҝһжҺҘеҲ°еӨҙдёҠеQҢиҝһжҺҘзҡ„зӮ№е°ұеҸҳжҲҗдә?/span>sеQҢиҝһжҺҘеҲ°һ®ҫдёҠеQҢиҝһжҺҘзҡ„зӮ№е°ұеҸҳжҲҗдә?/span>kеQүпјҢзӣҙеҲ°жү‘ЦҲ°дёҖдёӘжһҒеӨ§иҝһйҖҡеӯҗй“ҫпјҲдёҚиғҪеҶҚеңЁеү©дёӢзҡ„зӮ№дёӯжүҫеҲ°зӮ№ҳqһжҺҘеҲ°й“ҫзҡ„дёӨз«ҜдәҶеQүгҖ?/span>
3еQүз”ұдә?/span>kе’Ңеү©дёӢзӮ№йӣ?/span>R’жІЎжңүзӮ№зӣёҳqһпјҢжүҖд»ҘжҲ‘们еҸӘиғҪеңЁҳqҷжқЎй•үK“ҫдёҠжүҫе’?/span>kзӣёиҝһзҡ„зӮ№tеQҲеӣ дёЮZёҖе®ҡеҸҜд»ҘжүҫеҲҺНјҢдёЮZ»Җд№Ҳе‘ўеQ?/span>kжң¬инnдёҚе°ұжңүдёӘй“‘ЦҶ…зҡ„зӮ№ҳqһзқҖеҳӣпјҢдёҚ然е®ғе°ұжҳҜдёӘеӯӨз«ӢзӮ№дәҶеQ?/span>гҖӮжүҖд»ҘжүҫеҲ?/span>(k , t)зӣёиҝһеQҢеЖҲдё?/span>(s, t+1) зӣёиҝһеQҢ然еҗҺеҲ жҺ?/span>(t, t+1)ҳqҷжқЎиҫ№пјҢһ®ЮpғҪеӨҹеҫ—еҲоCёҖдёӘж–°зҡ„зҺҜдәҶпјҢеҰӮжһңжӯӨж—¶зҺҜзҡ„й•ҝеәҰдё?/span>nһ®Юq»“жқҹдәҶеQҢеҗҰеҲҷз‘фҫl?/span>1еQүгҖ?/span>
123 The sum
йҖ’жҺЁ
йўҳж„ҸеQҡжұӮж–җжҮLйӮЈеҘ‘ж•°еҲ—зҡ„第N(N <= 40)ҷеҸVҖ?/span>
йўҳи§ЈеQ?/span>__int64ж•°з»„йў„еӨ„зҗҶеҚіеҸҜгҖ?br />
124 Broken line
и®Ўз®—еҮ дҪ•: ҫUҝж®өеҲӨдәӨ
йўҳж„ҸеQҡеңЁтqійқўдёҠжңүдёҖдәӣй—ӯеҗҲзәҝҢDөпјҲжІЎжңүиҮӘдәӨе’Ңзӣёдә’дәӨеҸүпјүеQҢеҲӨж–ӯз»ҷе®ҡзҡ„зӮ?/span>PжҳҜеҗҰеңЁиҝҷдёӘй—ӯеҗҲзәҝҢDөеҶ…гҖ?/span>
йўҳи§ЈеQҡе…¶е®һе°ұжҳҜеҲӨж–ӯдёҖдёӘзӮ№жҳҜеҗҰеңЁеӨҡиҫ№еЕһеҶ…пјӣ
йҰ–е…ҲеQҢиҷҡжӢҹеҮәдёҖдёӘж— ҪIҜӮҝңзҡ„зӮ№QеQҢ然еҗҺз”ЁPQе’ҢжҜҸдёӘй—ӯеҗҲзәҝҢDөеҺ»еҒҡзӣёдәӨжЈҖӢ№?/span>(дёӨзәҝҢDөеҲӨдәӨеңЁй»‘д№ҰдёҠжңүиҜҰе°Ҫзҡ„и§ЈйҮ?/span>,дёҚеҶҚзҙҜиҝ°)гҖ?/span>
1) еҰӮжһңPеңЁжҹҗжқЎзәҝҢDөдёҠеQҢиҫ“еҮ?/span>BORDERеQ?/span>
2) еҰӮжһңPQе’ҢжүҖжңүзәҝҢDөдәӨзӮ№дёӘж•оCШ“еҘҮж•°еQҢиҜҙжҳҺеңЁеӨҡиҫ№еҪўеҶ…еQҢиҫ“еҮ?/span>INSIDEеQ?/span>
3) еҰӮжһңPQе’ҢжүҖжңүзәҝҢDөдәӨзӮ№дёӘж•оCШ“еҒ¶ж•°еQҢиҜҙжҳҺеңЁеӨҡиҫ№еҪўеӨ–еQҢиҫ“еҮ?/span>OUTSIDEеQ?/span>
125 Shtirlits
ж·ұеәҰдјҳе…ҲжҗңзғҰ + еүӘжһқ
йўҳж„ҸеQҡз»ҷе®ҡдёҖдёӘзҹ©йҳ?/span>B (3X3)еQ?/span>B[i][j]иЎЁзӨәA[i][j]еӣӣе‘ЁжҜ”е®ғеӨ§зҡ„ж•°зҡ„дёӘж•°еQҢжұӮж»ЎиғцжқЎдҡgзҡ?/span>AгҖ?/span>
йўҳи§ЈеQҡжһҡдё?/span>A[i][j]зҡ„жҜҸдёӘж•°еӯ—пјҢж•°еӯ—зҡ„иҢғеӣҙдШ“ [0,9]гҖӮеӨҚжқӮеәҰ109еQҢжүҖд»ҘйңҖиҰҒиҝӣиЎҢдёҖе®ҡзҡ„еүӘжһқгҖ?/span>
a) йҰ–е…ҲеQҢеҸҜд»ҘиӮҜе®ҡиҝҷB[i][j]дёӯдёҖе®ҡдјҡиҮӣ_°‘жңүдёҖдё?/span>0еQҢеӣ дёәжҖАLңүдёҖдёӘж•°жІЎжңүжҜ”е®ғеӨ§зҡ„ж•ҺНјҲй«ҳеӨ„дёҚиғңеҜ’е•Ҡ~~еQүгҖ?/span>еҜ№дәҺB[i][j] == 0зҡ„ж јеӯҗпјҢһ®?/span>A[i][j]и®ҫдШ“жңҖеӨ§еҖ?/span>9дёҖе®ҡдёҚдјҡй”ҷеQҢжүҖд»ҘеӨҚжқӮеәҰиҮӣ_°‘еҸҜд»ҘйҷҚеҲ° 108 дәҶгҖ?/span>
b) һ®?/span>Aзҡ„жҜҸдёӘйқһ9зҡ„ж јеӯҗж Үи®оCШ“-1еQҢ然еҗҺеҜ№жҜҸдёӘж јеӯҗҳqӣиЎҢжһҡдӢDеQҢжһҡдёҫиҢғеӣҙдШ“ [ 0, 8 ], еӣ дШ“B[i][j]дёәеӣӣе‘ЁжҜ”е®ғеӨ§зҡ„ж•°зҡ„дёӘж•?/span>, еҰӮжһңA[i][j]==9еQҢйӮЈд№?/span>B[i][j]еҝ…йЎ»дё?/span>0еQҢеӨҚжқӮеәҰйҷҚиҮі 98гҖ?/span>
c) жҜҸж¬ЎжһҡдӢDе®ҢжҜ•еQҢиҝӣе…ҘдёӢдёҖдёӘж•°зҡ„жһҡдёҫд№ӢеүҚпјҢҳqӣиЎҢе…ЁеұҖзҡ„жЈҖӢ№ӢпјҢеҜ№дәҺжҜҸдёӘж јеӯҗҫlҹи®Ўд»ҘдёӢж•°жҚ®еQ?/span>
i) е·Із»ҸжһҡдӢDзҡ„йӮ»еұ…ж јеӯ?/span> H
ii) жҖХd…ұжңүеӨҡһ®‘дёӘйӮХdұ…ж јеӯҗ T
iii) жҜ”иҮӘе·ұеӨ§зҡ„йӮ»еұ…ж јеӯ?/span> B
然еҗҺҳqӣиЎҢҪ{ӣйҖүпјҢеҰӮжһң
x) жҜ”еҪ“еүҚж јеӯҗеӨ§зҡ„йӮ»еұ…ж•°е·Із»Ҹӯ‘…еҮәйҷҗе®ҡеҖ?/span>, еҚ?/span> B > B[i][j]
y) жҜ”еҪ“еүҚж јеӯҗеӨ§зҡ„йӮ»еұ…ж•° + еү©дҪҷжңӘзҹҘйӮХdұ…ж•?/span> < ҫlҷе®ҡжҜ”е®ғеӨ§зҡ„йӮХdұ…ж•ҺНјҢ еҚ?/span> B + (T-H) < B[i][j]
еқҮдШ“ж— ж•Ҳи§ЈпјҢж— йңҖеҫҖдёӢжһҡдёҫпјҢеӣһжәҜгҖ?/span>
d) зӣҙеҲ°жүҖжңүж•°жһҡдӢDе®ҢжҜ•еQҢиҫ“еҮшҷ§ЈеҚӣ_ҸҜгҖ?/span>
126 Boxes
еҲқзӯүж•°и®ә
йўҳж„ҸеQҡеҜ№дәҺз»ҷе®ҡзҡ„Aе’?/span>BеQ?/span>
еҰӮжһңA > B, еҲҷзҠ¶жҖҒеҸҳдё?/span> (A-B, 2*B)
еҰӮжһңA < B, еҲҷзҠ¶жҖҒеҸҳдё?/span> (2*A, B-A)
еҪ?/span> A == B ж—УһјҢҫl“жқҹгҖ?/span>
иҰҒжұӮиҫ“еҮәҳqҷдёӘжғ…еҶөжҳҜеҗҰеӯҳеңЁеQҢеҰӮжһңеӯҳеңЁиҫ“еҮәеҸҳжҚўзҡ„ӢЖЎж•°еQҢдёҚеӯҳеңЁиҫ“еҮә-1гҖ?/span>
йўҳи§ЈеQҡж №жҚ®йўҳж„ҸпјҢеҸҜд»Ҙеҫ—еҮәдёҖдәӣз®ҖеҚ•зҡ„жҺЁи®әеQ?/span>
a) еҪ?/span>A == 0 жҲ–иҖ?/span> B == 0 ж—?/span> Ҫ{”жЎҲдё?/span> 0гҖ?/span>
b) жңҖеҗ?/span>A == Bзҡ„ж—¶еҖҷпјҢеҝ…е®ҡжҳ?/span>K = (A+B)/2еQҢжүҖд»ҘеҪ“A+BдёәеҘҮж•°ж—¶Ҫ{”жЎҲдёҚеӯҳеңЁгҖ?/span>
c) е®ҡд№үжңҖеҗҺзҡ„зҠ¶жҖҒдәҢе…ғз»„дё?/span> (K, K),
еҖ’ж•°ҪW¬дәҢӢЖЎзҡ„ж“ҚдҪңеҝ…е®ҡдё?/span> (3K/2,K/2) жҲ–иҖ?/span>(K/2,3K/2) (2ҝU?/span>)
еҖ’ж•°ҪW¬дёүӢЖЎзҡ„ж“ҚдҪңеҝ…е®ҡдё?/span> (7K/4, K/4) жҲ–иҖ?/span> (3K/4, 5K/4) жҲ–иҖ?/span> (5K/4, 3K/4) жҲ–иҖ?/span> (K/4, 7K/4) (4ҝU?/span>)
еҖ’ж•°ҪW¬еӣӣӢЖЎж“ҚдҪ?/span>(15K/8,K/8)... (8ҝU?/span>)
еҖ’ж•°ҪW?/span>iӢЖЎж“ҚдҪ?/span> ( (2(i-1)-1)/2(i-1) * K, 1/2(i-1) * K ) ... (2(i-1) ҝU?/span>)
d) Aе’?/span>Bзҡ„з»„еҗҲеҝ…е®ҡеңЁҳqҷдәӣжғ…еҶөдёӯжүҫгҖ?/span>
дәҺжҳҜе®ҡд№ү A = L1 / 2n * K, B = L2 / 2n * K (е…¶дёӯK = (A+B)/2, L1,L2дёәеҘҮж•ҺНјҢтq¶дё”(L1+L2) = 2(n+1))
еҫ—пјҡ
L1 = 2n * (A/K)
L2 = 2n * (B/K)
д»?/span> A = 2a * A', K = 2k * K'
еҲҷжңү L1 = 2(n+a-k) * A'/K' дёәеҘҮж•ҺНјҢжүҖд»?/span>n+a-k = 0еQҢеЖҲдё”иҰҒдҝқиҜҒA' mod K' == 0еQ?/span>A е’?/span> K йғҪдШ“е·ІзҹҘеQҢеҲҷеҸҜд»Ҙи®Ўз®—еҮ?/span> a гҖ?/span>A'гҖ?/span>kгҖ?/span>K'еQҢжңҖҫlҲзҡ„жӯҘж•°һ®ұжҳҜk-a+1гҖ?/span>
йңҖиҰҒжіЁж„Ҹзү№ҢDҠжғ…еҶөпјҡAжҲ?/span>Bдё?/span>0зҡ„жғ…еҶөпјҢд»ҘеҸҠA+BдёәеҘҮж•°зҡ„жғ…еҶөгҖ?/span>
127 Telephone directory
һ®ҶжүҖжңүз”өиҜқеҸ·з ҒжҢүйҰ–еӯ—жҜҚжҺ’еәҸпјҢҫlҹи®ЎжҜҸдёӘйҰ–еӯ—жҜҚеҮәзҺ°зҡ„ӢЖЎж•°AiеQ?Sum{ (Ai + K - 1 ) / K } + 2 һ®ұжҳҜҪ{”жЎҲгҖ?/p>
128 Snake
жғПxі•йў?/span>
йўҳж„ҸеQҡз»ҷе®?/span>NеQ?/span>4<=N<=10000еQүдёӘж•ҙж•°зӮ№пјҢй—®иғҪдёҚиғҪҫl„еҮәдёҖдёӘеӨҡиҫ№еЕһеQҢж»Ўӯ‘ід»ҘдёӢжқЎд»Уһјҡ
a) й—ӯеҗҲеQ?/span>
b) жүҖжңүзҡ„зӮҡwғҪжҳҜеӨҡиҫ№еЕһдёҠзҡ„зӮ№пјҢтq¶дё”еҸӘиғҪиў«з”ЁдёҖӢЖЎпјӣ
c) д»ЦMҪ•дёӨдёӘҳqһз®Ӣзҡ„зәҝҢDөйңҖиҰҒз»„жҲҗдёҖдё?/span>90еәҰзҡ„зӣҙи§’еQ?/span>
d) еӨҡиҫ№еҪўзҡ„жүҖжңүиҫ№йғҪиҰҒтqҢҷЎҢдәҺеқҗж ҮибuеQ?/span>
e) еӨҡиҫ№еҪўдёҚиғҪеӯҳеңЁиҮӘдәӨпјӣ
f) еӨҡиҫ№еҪўзҡ„е‘Ёй•ҝиҰҒж»Ўӯ‘ПxңҖһ®Ҹпјӣ
йўҳи§ЈеQ?/span>
1) еҜ№дәҺиҫ“е…Ҙзҡ„зӮ№дҝқеӯҳдёӨдҶҫж•°з»„PXгҖ?/span>PYеQҢеЖҲдё”и®°еҪ•жҜҸдёӘзӮ№еңЁеҺҹж•°з»„зҡ„дёӢж ?/span>indexеQ?/span>
2) еҜ?/span>PXҳqӣиЎҢXдјҳе…ҲжҺ’еәҸеQҢеҜ№PYҳqӣиЎҢYдјҳе…ҲжҺ’еәҸеQ?/span>
3) еҜ?/span>PXдёӯеәҸеҸ·дШ“еҘҮж•°зҡ„зӮ№PX[i]е’Ңе®ғзҡ„дёӢдёҖдёӘзӮ№PX[i+1]ҳqӣиЎҢyеҖјзҡ„еҲӨж–ӯеQҢеҰӮжһңиҝҷдёӨдёӘзӮ№зҡ„yеҖйgёҚзӣёзӯүеQҢйӮЈд№ҲиҜҙжҳҺиҝҷдёӘзӮ№ж— жі•еҠ е…ҘеӨҡиҫ№еҪўдёӯеQ?/span>PX[i]ж— жі•й…ҚеҜ№еQҢиў«еӯӨз«ӢдәҶпјүеQҢж— и§ЈгҖӮеҗҰеҲ?/span>PX[i].indexе’?/span>PX[i+1].indexеҝ…然жңүдёҖжқЎиҫ№еQҲеҸҜд»Ҙз”ЁйӮАLҺҘиЎЁжқҘеӯҳиҫ№е…ізі»еQҢеӣ дёәжңҖеҗҺжұӮзҡ„жҳҜдёҖдёӘеӨҡиҫ№еЕһеQҢжүҖд»ҘжҜҸдёӘзӮ№жңүдё”д»…жңүдёӨжқЎиҫ№пјҢе…¶е®һһ®ұжҳҜдёҖдёӘе“ҲеҜҶе°”ҷеҝеӣһи·ҜпјүгҖ?/span>
тq¶дё”еҠ?/span>PX[i+1].x - PX[i].index зҙҜеҠ еҲ°зӯ”жЎ?/span>ansдёӯпјӣ
4) еҜ?/span>PYдёӯзҡ„зӮ№дҪңе’?/span>3еQүдёҖж пLҡ„еӨ„зҗҶеQҢдҝқеӯҳиҫ№зҡ„е…іҫp»пјҢдҪҶжҳҜҳqҷйҮҢйңҖиҰҒеҲӨж–ӯдёҖҝUҚиҮӘдәӨзҡ„жғ…еҶөеQҢеҰӮеӣ?/span>1дёӯпјҢ3)ж“ҚдҪңе®ҢжҜ•еҗҺпјҢдә§з”ҹдёүжқЎиҫ?/span>(1,1) - (2,1) (1,2) -(3, 2) (2,3) - (3,3)еQӣйӮЈд№ҲеңЁҳqӣиЎҢж“ҚдҪң4еQүзҡ„ж—¶еҖ?/span>(1,1)-(1,2) е’?/span> (3,2) - (3, 3)йғҪжҳҜжІЎй—®йўҳзҡ„еQҢе”ҜзӢ?/span> (2,1) - (2,3) е’?/span> е…ҲеүҚзҡ„иҫ№ (1,2) -(3, 2) дјҡдс”з”ҹиҮӘдәӨпјҢҳqқеҸҚдә?/span>eҳqҷжқЎи§„еҲҷеQҢжүҖд»ҘйңҖиҰҒжЈҖӢ№ӢиҝҷҝUҚжғ…еҶү|ҳҜеҗҰеӯҳеңЁпјҢеҰӮжһңеӯҳеңЁеQҢйӮЈд№Ҳеҝ…з„¶ж— и§Јпјӣе…·дҪ“ӢӮҖӢ№Ӣж–№жі•еҫҲеӨҡпјҢдёҚеҶҚзҙҜиҝ°еQ?/span>
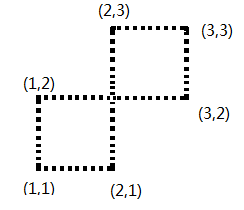
еӣ?/span>1
5) ҳqӣиҝҮ3)е’?/span>4)еҗҺпјҢеҶҚиҝӣиЎҢдёҖӢЖЎиҝһйҖҡжҖ§еҲӨж–ӯеҚіеҸҜпјҢд»ҘйҳІеӣ?/span>2зҡ„жғ…еҶьcҖ?/span>

еӣ?/span>2
129 Inheritance
и§ЈжһҗеҮ дҪ• + еҮёеҢ… + ҫUҝж®өеҲӨдәӨ
йўҳж„ҸеQҡз»ҷе®ҡдёҖдёӘеӨҡиҫ№еЕһе’ҢиӢҘтqІзәҝҢDөпјҢҳqҷдёӘеӨҡиҫ№еҪўеҶ…д»АL„ҸдёӨзӮ№ҳqһзәҝдёҚдјҡе’ҢеӨҡиҫ№еЕһиҫ№з•ҢзӣжҖәӨеQҢеҲҶеҲ«жұӮҳqҷдәӣҫUҝж®өеңЁеӨҡиҫ№еЕһеҶ…йғЁзҡ„й•ҝеәҰгҖ?/span>
йўҳи§ЈеQҡйҰ–е…ҲпјҢж ТҺҚ®“еӨҡиҫ№еҪўеҶ…д»АL„ҸдёӨзӮ№ҳqһзәҝдёҚдјҡе’ҢеӨҡиҫ№еЕһиҫ№з•ҢзӣжҖәӨ”еҸҜд»ҘиӮҜе®ҡҳqҷжҳҜдёӘеҮёеӨҡиҫ№еҪўпјҢдәҺжҳҜй—®йўҳһ®Юpқ{еҢ–жҲҗдәҶжұӮжҹҗжқЎҫUҝж®өе’ҢеҮёеӨҡиҫ№еҪўзӣёдәӨеҗҺҫUҝж®өеңЁеӨҡиҫ№еЕһеҶ…йғЁеҲҶзҡ„й•ҝеәҰгҖ?/span>
з”ЧғәҺҫlҷе®ҡзҡ„зӮ№жҳҜдШ•еәҸзҡ„еQҢжүҖд»ҘжңҖҪҺҖеҚ•зҡ„ж–ТҺі•жҳҜжұӮҳqҷдәӣзӮҡwӣҶзҡ„дёҖдёӘеҮёеҢ…пјҢжһ„йҖ еҮәдёҖдёӘжҢүзӮТҺҺ’еәҸзҡ„еӨҡиҫ№еҪўпјҢзӣ”RӮ»дёӨзӮ№ҳqһзәҝдёәеҺҹеӨҡиҫ№еҪўзҡ„дёҖжқЎиҫ№гҖ?/span>
йӮЈд№ҲжһҡдӢDжҜҸжқЎиҫ№е’Ңҫlҷе®ҡҫUҝж®өзҡ„зӣёдәӨжғ…еҶөпјҡ
1) дёҚзӣёдәӨпјҲтqҢҷЎҢеQүпјҢҫl§з®ӢеҲӨж–ӯдёӢдёҖжқЎиҫ№еQ?/span>
2) е…ЮqәҝеQҢзӣҙжҺҘиҹ©еҮәжһҡдёҫпјҢеQҲз”ұдәҺжҳҜеҮёеӨҡиҫ№еЕһеQҢж”№ҫUҝж®өиӮҜе®ҡдёҚеҸҜиғҪеңЁеӨҡиҫ№еҪўеҶ…еQүпјӣ
3) зӣжҖәӨеQҢе°ҶҳqҷдёӘдәӨзӮ№еӯҳе…ҘйӣҶеҗҲSеQ?/span>
һ®ҶеҺҹҫUҝж®өзҡ„дёӨдёӘз«ҜзӮ№еӯҳе…ҘйӣҶеҗ?/span>SеQҢеҜ№йӣҶеҗҲSзҡ„зӮ№ҳqӣиЎҢxеқҗж ҮйҖ’еўһжҺ’еәҸеQ?/span>xзӣёеҗҢж—?/span>yеқҗж ҮйҖ’еўһжҺ’еәҸеQүпјҢ然еҗҺжһҡдӢDзӣ”RӮ»дёӨдёӘзӮ№зҡ„дёӯзӮ№еQҢеҲӨж–ӯжҳҜеҗҰеңЁеңЁеҺҹеӨҡиҫ№еҪўеҶ…еQҢеҰӮжһңеңЁеQҢйӮЈд№Ҳе°ҶҳqҷдёӨдёӘзӣёйӮИқӮ№ҫlғжҲҗзҡ„зәҝҢDлҠҡ„й•ҝеәҰзҙҜеҠ еҲ°жңҖеҗҺзҡ„Ҫ{”жЎҲдёӯгҖӮеҰӮеӣ?/span>1дёЮZёӨдёӘдәӨзӮ№зҡ„жғ…еҶөгҖ?/span>
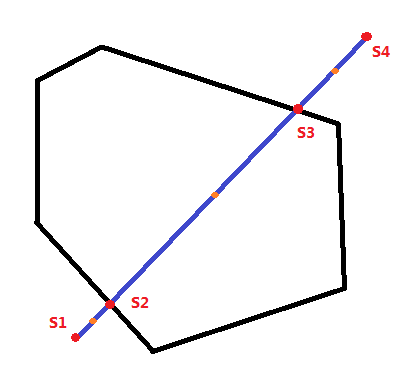
еӣ?/span>1
111 Very simple problem дәҢеҲҶжһҡдӢD
112 a^b-b^a дәҢеҲҶжұӮе№Ӯ
113 Nearly prime numbers ж•°и®әеQҡзҙ ж•°зӯӣйҖ?br />114 Telecasting station жһҡдӢD
115 Calendar ҪҺҖеҚ•жЁЎжӢ?/strong>
116 Index of super-prime еҠЁжҖҒ规еҲ’пјҡи®°еҝҶеҢ–жҗңзҙ?/strong>
117 Counting дәҢеҲҶжұӮе№Ӯ
118 Digital Root ж•°еӯҰйў?/strong>
119 Magic Pairs ж•°и®әеQҡжү©еұ•ж¬§еҮ йҮҢеҫ?/strong>
110 Dungeon
и®Ўз®—еҮ дҪ•еQҡе°„ҫUҝе’ҢзҗғдҪ“зӣжҖәӨ
йўҳж„ҸеQҡз»ҷе®ҡдёҖжқ?/span>3Dһ®„зәҝ е’?/span> NдёӘзҗғдҪ“пјҢй—®е°„ҫUҝзҡ„еҗ„з§ҚеҸҚеј№ҫlҸиҝҮзҡ„зҗғдҪ“зј–еҸшPјҢеҰӮжһңеҸҚе°„ӯ‘…иҝҮ10ӢЖЎпјҢеҸӘйңҖиҰҒиҫ“еҮәеүҚеҚҒж¬ЎгҖ?/span>
йўҳи§ЈеQҡеҫҲжҳҺжҳҫеQҢйҰ–е…ҲйңҖиҰҒжһҡдёҫжҜҸдёӘзҗғдҪ“е’ҢеҪ“еүҚһ®„зәҝзҡ„зӣёдәӨжғ…еҶөпјҢеҰӮжһңе’ҢеӨҡдёӘзҗғдҪ“зӣёдәӨиӮҜе®ҡжҳҜеҸ–и·қјӣАLңҖҳq‘зҡ„зҗғдҪ“ҳqӣиЎҢзӣжҖәӨи®Ўз®—еQҢ然еҗҺи®ЎҪҺ—еҮәҪIәй—ҙеҸҚе°„һ®„зәҝеQҢйҮҚеӨҚд»ҘдёҠж“ҚдҪ?/span>11ӢЖЎпјҢеҰӮжһңжҹҗж¬Ўзҡ„еҸҚһ®„е°„ҫUҝе·ІҫlҸдёҚиғҪе’Ңд»ЦMҪ•зҗғдҪ“зӣжҖәӨйӮЈд№ҲзӣҙжҺҘи·ӣ_ҮәҳqҷдёӘҳqҮзЁӢгҖ?/span>
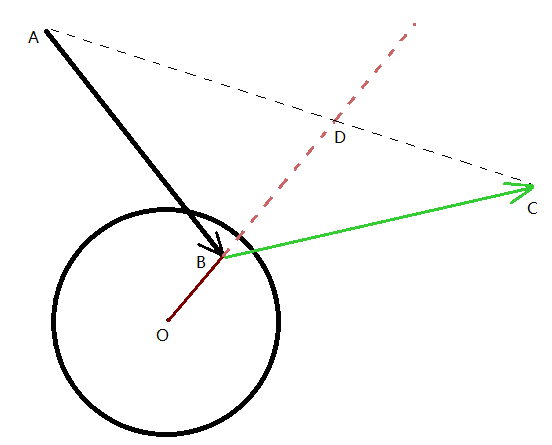
еӣ?
еҰӮеӣҫ1еQҢиЎЁҪCәе°„ҫU?/span>ABе’ҢзҗғOзӣжҖәӨдә?/span>BзӮ№пјҢеҸҚе°„еҗҺзҡ„һ®„зәҝдё?/span>BCеQ?/span>BDдёәзҗғеҝ?/span>OеҲоCәӨзӮ№зҡ„е»үҷ•ҝҫUҝпјҢйӮЈд№Ҳеҝ…е®ҡж»Ўиғцд»ҘдёӢеҮ дёӘжқЎдҡgеQ?/span>
е·ІзҹҘAзӮ№еқҗж ?/span>(xa, ya, za)еQҢеҚ•дҪҚеҗ‘йҮ?/span>tab
BзӮ№еқҗж ?/span> дё?/span> (xb, yb, zb) = (xa, ya, za) + |AB| * tab (1)
BзӮ№еңЁзҗ?/span>OдёҠпјҢжүҖд»?/span>BзӮ№еқҗж Үж»Ўӯ‘?/span>
| (xb, yb, zb) - (xo, yo, zo) | = OB = Ro (2)
һ®?/span>(1)д»Је…Ҙ(2)еQҢеҸҜи®Ўз®—еҮ?/span>|AB|зҡ„й•ҝеәҰпјҲз”ЧғәҺжҳҜе°„ҫUҝе’ҢзҗғдҪ“жұӮдәӨеQҢиҝҷдёӨдёӘж–№зЁӢжұӮеҮәжқҘзҡ„жҳҜзӣҙҫUҝе’ҢзҗғдҪ“зҡ„дәӨзӮ№пјҢжүҖд»ҘиҝҳйңҖиҰҒи®ЎҪҺ—ж–№еҗ‘еҲӨж–ӯдәӨзӮ№зҡ„еҸҜиЎҢжҖ§пјҢеҰӮжһңдәӨзӮ№жңүдёӨдёӘпјҢеҲҷеҸ–и·қзҰ»һ®Ҹзҡ„йӮЈдёӘеQҢеҰӮжһңеҸӘжңүдёҖдёӘдәӨзӮ№пјҢиҜҙжҳҺжҳҜзӣёеҲҮпјүеQҢ然еҗҺеҲ©з”?/span>(1)ејҸи®ЎҪҺ—еҮәBзӮ№еқҗж ҮгҖ?/span>
2) һ®„зәҝҫlҸиҝҮзҗғдҪ“зҡ„еҸҚһ®„е°„ҫU?/span>
еҒҮи®ҫCзӮ№еңЁAҫlҸиҝҮBзӮ№еҸҚһ®„еҗҺзҡ„еҸҚһ®„е°„ҫUҝдёҠеQҢеЖҲдё?/span>AB = BCеQҢйӮЈд№?/span>ACеҝ…е®ҡе’?/span>OBе»үҷ•ҝҫUҝзӣёдәӨпјҢеҒҮи®ҫдәӨдәҺDзӮ№пјӣ
еҚ•дҪҚеҗ‘йҮҸcos(ABD) = Iba * IbdеQ?/span>
BD = AB * cos(ABD)еQ?/span>
еҗ‘йҮҸAD = еҗ‘йҮҸAB + еҗ‘йҮҸBDеQ?/span>
еҗ‘йҮҸAC = 2 * ADеQ?/span>
зӮ?/span>C (xc, yc, zc) = еҗ‘йҮҸAC + (xa, ya, za)еQ?/span>
еҗ‘йҮҸBCжұӮеҮәеҗҺиҝ”еӣ?/span>1) ҫl§з®ӢеҲӨж–ӯе’ҢеҲ«зҡ„зҗғзҡ„зӣёдәӨжғ…еҶөпјӣ
111 Very simple problem
дәҢеҲҶҪ{”жЎҲ + еӨ§ж•°жЁЎжӢҹ
йўҳж„ҸеQҡз»ҷе®?/span>X( X <= 10100)еQҢжұӮXејҖж–№еҗҺзҡ„дёӢеҸ–ж•ҙгҖ?/span>
йўҳи§ЈеQҡж•°ҫl„жЁЎжӢҹеӨ§ж•°гҖӮдәҢеҲҶзӯ”жЎ?/span>AеQҢжүҫж»Ўиғц A*A <= X жңҖеӨ§зҡ„AеҚідШ“Ҫ{”жЎҲгҖ?/span>
112 a^b-b^a
дәҢеҲҶжұӮе№Ӯ + еӨ§ж•°жЁЎжӢҹ
йўҳж„ҸеQҡжұӮ ab - ba ( 0 < a, b < 100)гҖ?/span>
йўҳи§ЈеQҡж•°ҫl„жЁЎжӢҹеӨ§ж•°гҖӮдәҢеҲҶжұӮ ABгҖ?/span>
еҪ?/span> B == 0 еҲ?AB = 1; еҗҰеҲҷ AB = (A2)(B/2) * ( (B mod 2) ? A : 1 ); йҖ’еҪ’жұӮи§ЈгҖ?/p> 113 Nearly prime numbers зҙ ж•°Ҫ{ӣйҖ?/span> + зҙ ж•°еҲӨе®ҡ йўҳж„ҸеQҡеҲӨж–ӯдёҖдёӘж•°жҳҜеҗҰдёЮZёӨдёӘзҙ ж•°зҡ„ҝUҜгҖ?/span> йўҳи§ЈеQҡеҲ©з”Ёдј ҫlҹзҡ„зҙ ж•°Ҫ{ӣйҖүе°Ҷ 1-31623 зҡ„зҙ ж•°зӯӣйҖүеҮәжқҘпјҢ31623дёәег^ж–№еӨ§дәҺзӯүдә?/span>109зҡ„жңҖһ®Ҹж•ҙж•ҺНјҢеӣ дШ“дёҖдёӘж•°зҡ„ејҖж–№еҶ…жүҫдёҚеҲоCёҖдё?йқ?жҲ–е®ғжң¬инn)еӣ еӯҗзҡ„иҜқе®ғжң¬нw«е°ұжҳҜзҙ ж•ҺНјҢжүҖд»Ҙзҙ ж•°еҸӘйңҖиҰҒзӯӣйҖүеҲ° 109 зҡ„ејҖж–?/span> еҚӣ_ҸҜгҖ?/span> еҜ№дәҺжҜҸдёӘж•ҺНјҢйҒҚеҺҶзҙ ж•°ж•°з»„еQҢеҰӮжһңиғҪиў«жҹҗдёӘзҙ ж•°ж•ҙйҷӨпјҢеҲӨж–ӯе•ҶжҳҜдёҚжҳҜдёҖдёӘзҙ ж•ҺНјҢеҰӮжһңе•Ҷд№ҹжҳҜзҙ ж•°з»“жһңдШ“YesеQҢеҗҰеҲҷдШ“NoгҖ?/span> 114 Telecasting station жһҡдӢD + ҫlҹи®Ў йўҳж„ҸеQҡеңЁXиҪҙдёҠ规е®ҡдёҖдәӣжңүжқғеҖ?/span>aiзҡ„зӮ№ (x1,a1), (x1,a1), (x2,a2) .. (xn,an)иҰҒжұӮең?/span>xеқҗж ҮдёҠжүҫеҲоCёҖдёӘзӮ№XдҪҝеҫ— M = |X-x1|*a1 + ... |X-xn|*an зҡ„еҖјжңҖһ®ҸгҖ?/span> йўҳи§ЈеQҡз»Ҷеҝғи§ӮеҜҹеҸҜд»ҘеҸ‘зҺҺНјҢMжҳҜе…ідә?/span>Xзҡ„дёҖӢЖЎеҮҪж•ҺНјҢжүҖд»ҘеҸҜд»ҘзЎ®е®?/span>Xеҝ…е®ҡдё?/span> x1...xnдёӯзҡ„жҹҗдёӘзӮҸVҖ?/span> з”ЧғәҺеҺҹејҸдёӯеӯҳеңЁз»қеҜ№еҖы|јҢдёЮZәҶһ®Ҷз»қеҜ№еҖјеҢ–ҪҺҖеQҢеҸҜд»Ҙе°ҶXзҡ„еҢәй—ҙеҲҶҢDөпјҢжҜ”еҰӮеҪ?/span>X дё?/span> xjж—¶еҸҜд»Ҙз®ҖеҢ–дШ“ M = (X-x1)*a1 + ...(X-xj)*aj + (xj+1-X)*aj+1 + ... + (xn-X)*an = (X * presum[j] - preproduct[j]) + (postproduct[j+1] - X * postsum[j+1]) ҳqҷдәӣиҫ…еҠ©ж•°з»„еҸҜд»ҘйҖҡиҝҮеӣӣж¬ЎҫUҝжҖ§жү«жҸҸеҫ—еҮәпјҢеӨҚжқӮеә?/span>O(n)гҖ?/span>然еҗҺеQ?/span>е…Ҳе°ҶxiйҖ’еўһжҺ’еәҸеQҢжһҡдёҫжҜҸдё?/span>xiеQҢи®ЎҪҺ—жңҖһ®ҸеҖјжӣҙж–?/span>MеQҢе°ұеҸҜд»Ҙең?/span>O(n)зҡ„ж—¶й—ҙеҶ…жұӮи§ЈдәҶгҖӮжҖЦMҪ“ҪҺ—жі•еӨҚжқӮеәҰдШ“жҺ’еәҸеӨҚжқӮеә?/span>O(n log n)гҖ?br /> ҪҺҖеҚ•жЁЎжӢ?/span> йўҳж„ҸеQҡз»ҷе®ҡдёҖдёӘжңҲд»?/span>Mе’ҢеӨ©ж•?/span>NеQҢжұӮ2001зҡ„йӮЈдёҖеӨ©жҳҜжҳҹжңҹеҮ гҖ?/span> йўҳи§ЈеQҡеҸҜд»Ҙйў„еӨ„зҗҶеҮәжҜҸдёӘжңҲзҡ„еӨ©ж•ҺНјҢеҰӮжһңеӨ©ж•°еӨ§дәҺйӮЈдёӘжңҲеҜ№еә”зҡ„еӨ©ж•°жҲ–иҖ…жңҲж•°еӨ§дә?/span>12иӮҜе®ҡжҳҜдёҚеҸҜиЎҢзҡ„пјҢеҗҰеҲҷһ®Ҷз»ҷе®ҡжңҲж•?/span>Mд№ӢеүҚзҡ?/span> 1еҲ?/span>M-1дёӘжңҲзҡ„еӨ©ж•°зӣёеҠ еҶҚеҠ дёҠNеҫ—еҲ°SumеQ?/span>Sum mod 7һ®ұеҸҜд»Ҙе®ҡдҪҚеҲ°жҳҹжңҹеҮ дәҶгҖ?/span>
зҙ ж•°Ҫ{ӣйҖ?/span> + и®°еҝҶеҢ–жҗңзҙ?/span>(жҲ?/span> еҠЁжҖҒ规еҲ?/span>) йўҳи§ЈеQҡе…Ҳһ®Ҷж»Ўӯ‘ПxқЎд»¶зҡ„ ӯ‘…зс”зҙ ж•° Ҫ{ӣйҖүеҮәжқҘпјҢ3 5 11 17Ҫ{үзӯүеQ?/span>然еҗҺеҜ№дәҺиҫ“е…Ҙзҡ?/span>NҳqӣиЎҢдёҖӢЖЎи®°еҝҶеҢ–жҗңзғҰеQ?/span>DPеQ?/span> дҫӢеҰӮ N = 15 йӮЈд№ҲNзҡ„жңҖдјҳеҖйgёҖе®ҡжҳҜжқҘиҮӘ 15-3=12еQ?/span>
15-5=10еQ?/span> 15-11=4 ҳqҷдёүдёӘж•°еQ?/span>д»ҘжӯӨҫcАLҺЁеQҢйҖ’еҪ’еҮәеҸЈжҳ?/span>N = 0еQҢжҜҸӢЖЎи®ЎҪҺ—е®ҢNһ®ұе°Ҷе®ғдҝқеӯҳдёӢжқҘпјҢдёӢж¬Ўһ®ЧғёҚз”ЁйҮҚеӨҚи®ЎҪҺ—дәҶгҖ?/span> жүҖд»ҘзҠ¶жҖҒиқ{ҝUАL–№ҪEӢдШ“еQ?/span>DP[i] =
min{ DP [ i - p ] , p дёшҷ¶…ҫU§зҙ ж•?/span> } + 1 еӣ дШ“йңҖиҰҒиҫ“еҮәз»„еҗҲзҡ„еәҸеҲ—еQҢжүҖд»ҘжҜҸӢЖЎжҗңзҙўпјҢйңҖиҰҒдҝқеӯҳеҪ“еүҚжңҖдјҳеҖјзҡ„еүҚй©ұҫl“зӮ№еQҢжңҖеҗҺдёҖӢЖЎжҖ§иҫ“еҮәеҚіеҸҜгҖ?/span> дәҢеҲҶжұӮдҪҷ йўҳж„ҸеQҡз»ҷе®?/span>N(N < 10001)дёӘж•°AiеQҢжұӮе…¶дёӯAiM
жҳ?/span>Kзҡ„еҖҚж•°зҡ„ж•°зҡ„дёӘж•°гҖ?/span> йўҳи§ЈеQ?/span>еҜ№дәҺab mod cдәҢеҲҶжұӮи§ЈгҖ?/span>еҪ?/span>
b == 0 еҲ?nbsp;ab mod c = 1 mod c; еҗҰеҲҷ ab mod c = (A2)(B/2)
* ( (B%2) ? A : 1 ) mod c; ж•°еӯҰеҪ’зәіжі?/span> йўҳж„ҸеQ?/span>е®ҡд№үf(n) дё?/span> nзҡ„жүҖжңүж•°еӯ—зҡ„е’?/span>. еҰӮжһң f(n) жҳ?/span>1дҪҚж•°еӯ—пјҢйӮЈд№Ҳе®ғжҳҜnзҡ?/span> "digital root"еQҢеҗҰеҲ?/span>nзҡ?/span>"digital root" дё?/span> f(n) зҡ?/span>"digital root"гҖ?br /> ҫlҷе®ҡж•°з»„AiеQҢжұӮ A1*A2* … *AN + A1*A2*…*AN-1 + … + A1*A2 + A1 зҡ?/span>"digital root"(N <= 1000)гҖ?/span> йўҳи§ЈеQҡе®ҡд№?/span>d(n)дё?/span>nзҡ?/span>"digital root"еQ?/span>еҲ©з”Ёж•°еӯҰеҪ’зәіжі•еҸҜиҜҒжҳҺ(д»?/span>N=1зҡ„жғ…еҶлҠҪ‘дёҠйҖ’жҺЁ)еQ?/span> 1) d( A1*A2* … *AN ) = d( AN * d( A1*A2* … *AN-1 ) ) 2) d(A1 + A2 ) = d( d(A1) +d(A2) ) еҲ©з”ЁҳqҷдёӨзӮ№пјҢеҸҜд»ҘзӣҙжҺҘжү«жҸҸAж•°з»„һ®ұеҸҜд»Ҙи®ЎҪҺ—еҮәҫlҷе®ҡиЎЁиҫҫејҸзҡ„"digital root"дәҶгҖ?/span> жһҡдӢD + жү©еұ•ӢЖ§еҮ йҮҢеҫ— йўҳж„ҸеQҡеҜ№дәҺжүҖжңүзҡ„(X,Y)еңЁж»Ўӯ‘?/span> (A0 * X + B0 * Y) % N = 0 (1) зҡ„жғ…еҶөдёӢ,дҪҝеҫ—(A * X + B * Y) % N = 0 (2) д№ҹжҲҗз«?/span>, жұӮиҝҷж пLҡ„ (A, B)гҖ?/span> йўҳи§ЈеQҡйҰ–е…ҲжұӮеҮ?/span>A0гҖ?/span>B0гҖ?/span>NдёүиҖ…зҡ„GCDеQҢжңҖеҗҺз®—еҮәжқҘзҡ„зӯ”жЎҲйңҖиҰҒд№ҳдёҠиҝҷдё?/span>GCDгҖ?/span> (A0 * X + B0 * Y) = K * N (3) (Kдёәж•ҙж•?/span>) (A * X + B * Y) = K' * N (4) (K'дёәж•ҙж•?/span>) X = (K*N - B0*Y) / A0 д»Је…Ҙ(4)еј?/span>,еҸҜеҫ— A*(K*N - B0*Y) + B*A0*Y = K'* N * A0 (5) еҢ–з®Җеҫ?/span> (6) (B*A0 - A*B0) * Y = (K'*A0 - K*A) * N (6) дёӨиҫ№еҗҢж—¶mod N еҫ?/span> (B*A0 - A*B0) * Y % N = 0 (7) з”ЧғәҺYдёЮZ“Qж„Ҹж•ҙж•?/span>(еҚ?/span>YжңүеҸҜиғҪе’ҢNдә’зҙ ), жүҖд»Ҙеҝ…ҷеАL»Ўӯ‘?/span> (B*A0 - A*B0) % N = 0 (8) еҸҜд»ҘеҢ–з®Җдё?/span> (B*A0 - A*B0) = K'' * N (9) (K''дёәж•ҙж•?/span>) A0 * B + N * (-K'') = A*B0 (10) жһҡдӢDAзҡ„еҖы|јҢһ®ұеҸҜд»ҘжҠҠж–№зЁӢиҪ¬еҢ–жҲҗдәҶ ax + by = cзҡ„еЕһејҸпјҢе…¶дёӯ: a = A0, b = N, c = A*B0 x = B, y = -K'' еҲ©з”Ёжү©еұ•ӢЖ§еҮ йҮҢеҫ—еҚӣ_ҸҜжұӮеҫ—жңҖһ®Ҹзҡ„ж»ЎиғцжқЎдҡgзҡ?/span>x(еҚ?/span>B)зҡ„еҖйgәҶгҖ?/span> жңҖеҗҺзҡ„Ҫ{”жЎҲйңҖиҰҒд№ҳдё?/span> A0гҖ?/span>B0гҖ?/span>N дёүиҖ…зҡ„GCDгҖ?/span> 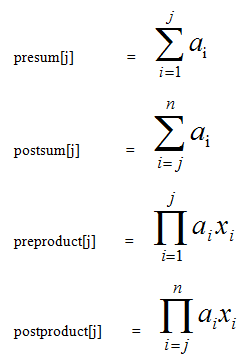
еӣ?
115 Calendar
йўҳж„ҸеQҡи¶…ҫU§зҙ ж•°жҳҜзҙ ж•°дёӢж Үд№ҹжҳҜзҙ ж•°зҡ„ж•°еQҢз»ҷе®ҡдёҖдёӘж•°NеQҢй—®ҳqҷдёӘж•°иғҪдёҚиғҪиў«дёҖдәӣи¶…ҫU§зҙ ж•°з»„еҗҲеҮәжқҘпјҢеҰӮжһңеҸҜд»ҘеQҢйңҖиҰҒж»Ўӯ‘Ңҷ¶…ҫU§зҙ ж•°зҡ„дёӘж•°жңҖһ®‘пјҢиҰҒжұӮиҫ“еҮәдёҖдёӘж–№жЎҲгҖ?/span>
118 Digital Root