130 Circle 數(shù)學：卡特蘭數(shù)
131 Hardwood floor 動態(tài)規(guī)劃：狀態(tài)壓縮132 Another Chocolate maniac 動態(tài)規(guī)劃：狀態(tài)壓縮133 Border 簡單統(tǒng)計134 Centroid 簡單統(tǒng)計135 Drawing Lines 遞推136 Erasing Edges 數(shù)學：一次方程137 Funny Strings 枚舉138 Games of chess 貪心139 Help Needed! 數(shù)學：逆序數(shù)相關(guān)性質(zhì)130 Circle 卡特蘭數(shù)
題意：給定一個圓，上面有2K個點，這2K個點可以互相連接，一個點只能連一次，問連接完畢將圓分割成最小的平面數(shù)的分割種類數(shù)。
題解：
1）首先K=1，最小平面為2，種數(shù)為f[1] = 1種。
2）然后考慮K=2的情況，將K0和K1連，那么剩下的情況就是K=1的情況，將K0和K3連，那么剩下的也是K=1的情況，所以K=2的情況為f[0]*f[1] + f[1]*f[0] = 2, 分割的平面數(shù)為3。
3）按照和K=2一樣的遞推方式，K = 5 時的情況為：
K0 - K1 -> f[0] * f[4]
K0 - K3 -> f[1] * f[3]
K0 - K5 -> f[2] * f[2]
K0 - K7 -> f[3] * f[1]
K0 - K9 -> f[4] * f[0]
于是可以得出遞推式： f[i] = sum { f[j] * f[i-1-j] 0 <= j < i }
131 Hardwood floor
動態(tài)規(guī)劃：狀態(tài)壓縮
方塊A 
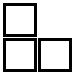方塊B
圖1
題意：利用以上兩種積木（任意數(shù)量，可進行旋轉(zhuǎn)），拼出一個M*N( 1<= M <= 9, 1 <= N <= 9)的矩形，問這樣的方式有多少種。如M = 2, N = 3 的情況 
，有以下5種拼接方式：
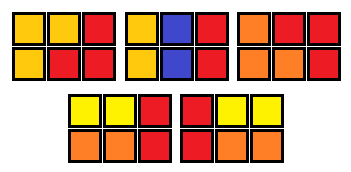
圖2
題解：考慮到N和M都很小，所以可以將每一行的狀態(tài)壓縮在一個二進制的整數(shù)中，0表示沒有放置，1表示已經(jīng)放置，圖3的第一行狀態(tài)就可以表示成101000（二進制表示，紫羅蘭色表示上一行延伸過來的方塊，灰色表示暫時沒有放置方塊的格子）。這樣就可以通過枚舉第i行的所有狀態(tài)，擴展出第i+1行的所有狀態(tài)。
舉例說明：
如圖3，枚舉到第i行的狀態(tài)為 101000（二進制數(shù)，實際操作的時候是轉(zhuǎn)化成十進制然后通過位運算來變換狀態(tài)的），假設對于當前狀態(tài)的所有解的情況已經(jīng)求出來，為DP[i][101000]，然后可以通過枚舉列將第i行填滿。并且要記錄下當前行狀態(tài)now = 101000, 下一行狀態(tài) next = 000000。
那么接下來一步就要開始枚舉列了，當枚舉到第一列時，發(fā)現(xiàn)當前格子已經(jīng)被i-1行所占據(jù)，所以直接進入下一列，這一列為空，所以我們需要某種方式將它填滿，對于圖3的情況，一共有三種填充方式(圖3、圖4、圖5)，因為格子不能重疊，所以在枚舉的時候需要判斷當前方塊放入的時候會不會導致和之前放置的方塊重疊，如果不會重疊說明狀態(tài)可達，否則不進入下一次迭代。
now = 101000 next = 000000
圖3
now = 111000 next = 110000
圖4
now = 111000 next = 010000
圖5
now = 111000 next = 011000
圖6
圖3的狀態(tài)一共生成三種狀態(tài)，然后我們繼續(xù)對生成的狀態(tài)進行擴展。以圖5的狀態(tài)為例，對它的狀態(tài)進行擴展，可以得到以下幾種狀態(tài)（橙色表示當前放入的方塊）：
1)放置一個橫躺的方塊A
now = 111110 next = 010000
圖7
2)放置一個豎著的方塊A
now = 111100 next = 010100
圖8
3)放置一個 "反7" 字 方塊B
now = 111110 next = 010100
圖9
4)放置一個 "L"字 方塊B
now = 111100 next = 010110
圖10
5)放置一個 "7" 字方塊 B
now = 111110 next = 010010
圖11
6)放置一個 "反L"字 方塊 B
now = 111100 next = 011100
圖12
枚舉列的過程是用dfs遞歸實現(xiàn)的，遞歸出口為列數(shù)col == N的時候，那時候當前行的狀態(tài)now一定是 2N - 1，因為要保證第i行能夠被填充滿，于是就可以得出狀態(tài)轉(zhuǎn)移方程DP[i+1][ next ] += DP[i][ now ]。
繼續(xù)枚舉第i+1行的所有狀態(tài)，擴展i+2行的可達狀態(tài)。
然后就要考慮初始狀態(tài)的情況，可以虛擬出一個第0行，那么第0行的狀態(tài)除了2N-1的情況為1，其他必定是0（因為是虛擬出來的，可以理解為全部填滿的狀態(tài)）。然后通過第0行的這個狀態(tài)可以迭代計算出第1行的各種可達狀態(tài)的解數(shù)。直到第M行，最后解的情況是DP[M+1][0]的值而非DP[M][2N-1]（因為枚舉到第M行后，第M行的非全滿的狀態(tài)也可以導致最后的格子鋪滿）。
132 Another Chocolate Maniac
動態(tài)規(guī)劃：狀態(tài)壓縮
題意：給定一個M*N (M <= 70, N <= 7)的棋盤，求放置最少數(shù)量的多米諾骨牌(大小為2X1)，使得它不能再放置更多的骨牌，給定的棋盤某些點不能被放置。
題解：沿用131那題的思路，但是這題只知道前一行的狀態(tài)是不夠的（因為多米諾骨牌的大小為2X1），考慮下面這種情況：
圖1
現(xiàn)在需要推導第i+2行的狀態(tài)，考慮在(i+2, 4)（紅色方塊）上如果不放置骨牌是否合法，那么由于(i+1, 4)為空，但是我們無法知道第i行的那個？格子到底是空還是非空，所以無法對紅色格子進行狀態(tài)轉(zhuǎn)移，所以需要將狀態(tài)表示稍作變形。
對于每一行用一個3進制的整數(shù)表示當前一行的狀態(tài)，定義以下常量：
#define STATE_PRE_EMPTY 0 // 上一行對應格為空
#define STATE_PRE_FULL 1 // 上一行對應格為滿
#define STATE_NOW_FULL 2 // 當前行對應格為滿
那么圖1的情況就可以表示成下面的狀態(tài)：
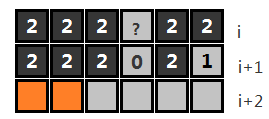
圖2
？格子所代表的的狀態(tài)就可以通過i+1行的那個值來確定了，i+1行對應列的格子值為0，表示第i行對應列的格子為未放置狀態(tài)（再上一行的狀態(tài)就不需要關(guān)心了，因為骨牌的最大長度為2）。
那么如果前一行對應列的狀態(tài)值為0的時候，必須放置一個骨牌（如果因為有障礙無法放置，那么說明這個狀態(tài)無法往下轉(zhuǎn)移了）。知道方法之后，具體做法就是初始化狀態(tài)，這里我們?yōu)榱诉\算簡便，可以虛擬出一個第零行來，對于第0行，它一定是全部塞滿的，所以第0行只有一個合法狀態(tài)，即：DP[0][ 3N - 1 ] = 0（每格的狀態(tài)都是2，最小骨牌數(shù)為0）,然后通過這個狀態(tài)，進行行枚舉，每一行進行列位移（可以采用dfs實現(xiàn)），將上一行的狀態(tài)推導產(chǎn)生下一行的可行狀態(tài)，每次dfs模擬放置和不放置兩種情況；
最后DP[M+1][ 3N - 1 ]就是最后的答案。
133 Border
簡單統(tǒng)計
題意：給定N(N <= 16000)個整數(shù)對(Ai, Bi)，如果存在一個整數(shù)對(A j, Bj) 使得 Aj < Ai 并且Bi < Bj 則稱(Ai, Bi)是多余的，問整數(shù)對中有多少是多余的。
題解：將整數(shù)對按Ai遞增排序，然后遍歷Bi記錄最大值，每次遇到比最大值小的可以斷定一定是多余的，計數(shù)器加1。知道遍歷完畢輸出即可。
134 Centroid
枚舉 + 樹形統(tǒng)計
題意：給定一棵樹，刪除樹上的某個結(jié)點（以及它所附帶的邊）i，剩下的各個連通塊中結(jié)點數(shù)目最大值為Ti，求 M = Min{Ti 1<= i <= n}，并且輸出刪除哪些點，能得到這個最小值M。
題解：遍歷一棵樹，并且用sum[i]記錄以i為根結(jié)點的樹的結(jié)點數(shù)目，通過一次遍歷就能把所有的sum求出來。記錄M = n；然后遍歷根結(jié)點，對于刪除i結(jié)點，剩下連通塊中的最大值為 max( n - sum[v], max{sum[v] v為i個直接子結(jié)點} )。同樣一次遍歷就能將所有的值求出來。
135 Drawing Lines
公式題
答案：n(n+1)/2 + 1
只是奇怪不能寫成 while (scanf("%d", &n) ！= EOF) 的形式，會PE。
136 Erasing Edges
數(shù)學題
題意：給定一個多邊形S的N條邊的中點，求這個多邊形S。
題解：假設原多邊形中點集合為Ci，多邊形點集合Pi。
假設 第0個點P0 = (x, y)，那么第一個點的坐標可以通過C0計算出來，即P1 = 2*C0 - P0,同理第二個點可以通過C1計算出，并且可以用P0的一次函數(shù)來表示，做n-1次迭代就可以把Pn-1用P0表示出來，而 Pn-1 + P0 = Cn-1，所以x，y都可以通過一次線性方程求出解來（也有可能有無解的情況）。然后再做n-1次迭代將所有點求出來即可。
137 Funny Strings
記憶化搜索
題意：對于一個序列S1, S2, S3 ... SN, 如果S1+1, S2, S3 ... SN-1進過一些左移或者右移幾次操作，可以和原序列保持一致，則稱這個序列為Funny String，給定N和K，求長度為N，和為K的Funny String。
題解：首先考慮，左移后第幾位和原來的第一位對應，可以假設是第i位吧，那么有以下關(guān)系式：
S[1] + 1 = S[i] ... (1)
S[2] = S[i+1] ... (2)
S[3] = S[i+2] ... (3)
......
S[j] = S[1] ... (N-i+2)
S[j+1] = S[2] ... (N-i+3)
......
S[n-1] = S[i-2] ... (N-1)
S[n] - 1 = S[i-1] ... (N)
顯然i不可能為1，因為S[1] + 1 != S[1]
并且GCD(N, (i-1)) 必須為1，否則這個等式組會存在內(nèi)環(huán)，無法求解。
接下來就可以通過記憶化搜索將S[2] ... S[N] 的值都用S[1] 表示出來。
表示方式有很多種，例如用一個二元組Tk = (ak, bk)來保存對于前一項的系數(shù)，
例如：
S[i] 可以表示為 Ti = (1, 1) (即 S[i] = 1 * S[1] + 1)
S[i+1] 可以表示為 Ti+1 = (1, 0) (即 S[i+1] = 1 * S[2] + 0)
這里的S[2]尚未計算出來，所以需要遞歸計算，具體計算方法第j項的方法如下：
getS ( j )
if j == i
return (1, 1)
else if j == i - 1
(ta, tb) = getS(n)
return (ta, tb - 1)
else if j > i
return getS( j - i + 1)
else if j < i
return getS(N + j - (i-1))
遞歸原因來自上面那N個等式，其中ta一定為1，tb為1或0。
所以這題的做法就是枚舉左移點i，計算出所有數(shù)對于S[1]的一次線性表示形式，然后利用所有數(shù)之和為K這個條件，求出非負整數(shù)S[1]，就能將所有數(shù)都求出來了。
138 Games of Chess
貪心
題意：給定N(N <= 100)個人的比賽場數(shù)X[i]，需要構(gòu)造一個比賽安排，假設G表示所有人的參賽場數(shù)之和，一共G/2場比賽，那么需要輸出G/2行，每行為a b，a、b表示參賽隊員的編號，其中a不等于b，并且a是勝利方，當前場的勝利方需要在上一場比賽中出現(xiàn)過（類似不斷淘汰的機制）。
題解：將每個人的參賽場數(shù)X[i]從大到小排序，如圖1所示，共有八位參賽選手，參賽場數(shù)分別為4、3、2、1、1、1、1、1，總和為14，所以總共有7場比賽。從第一個選手開始，將他的前X[i] - 1場比賽在賽程表的前X[i] - 1個位置的勝場中填滿，他的最后一場比賽和場數(shù)次多的人比，并且輸?shù)簦瑢鰯?shù)次多的人的剩余場數(shù)按照同樣的方式去填賽程表，直到所有比賽的勝利方都確定（即表中左邊那一列不為空），然后將剩下的還有剩余比賽的填在失敗方即可。
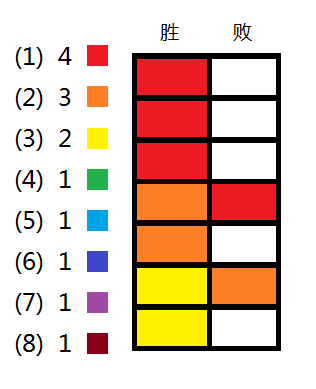
圖1
139 Help Needed!
數(shù)學證明
題意：如圖，給定一個亂序的十六數(shù)碼，問是否能通過一些移動，將它恢復到初始狀態(tài)（0的位置表示空缺位置，非0位置上的方塊可以向0移動，移動只能在上下左右四個方向進行）。
圖1
題解：只需要判斷 當前狀態(tài)數(shù)碼的逆序數(shù) 和 0到目標點曼哈頓距離 的奇偶性 即可。
證明如下：
首先將目標數(shù)碼排成一排，計算它的逆序數(shù)為15（為了便于理解，將每一行的數(shù)碼涂成不同的顏色）。
圖2
然后來看任意狀態(tài)的逆序數(shù)：
圖3
I）如圖3，考慮當前狀態(tài)下的水平移動，即X可以向0移動，Y也可以向0移動（也可以理解成兩個方塊的交換）。對于這兩種情況：
1) X 和0交換(X
> 0)，交換后的數(shù)碼，逆序數(shù)-1；
2) Y 和0交換(Y
> 0)，交換后的數(shù)碼，逆序數(shù)+1；
圖4
II）如圖4，考慮當前狀態(tài)下的豎直移動，即A可以向0移動，B也可以向0移動。
由于兩者情況是一樣的，這里只介紹A和0交換的情況。
假設A和0中間的三個方塊（十六數(shù)碼，一定是三個方塊）中比A小的有x個，那么比A大的就是(3-x)個，這三個方塊的本身逆序數(shù)為K，那么：
1）交換前，A 到0
這個區(qū)間段的逆序數(shù)為 x + 1 + K + 3;
2）交換后，A 到0
這個區(qū)間段的逆序數(shù)為 (3-x) + K;
交換前后逆序數(shù)的差值為 (3-x) + K - (x + 1 + K + 3) = -2x - 1;
綜合I 、II發(fā)現(xiàn)，每進行一次交換，逆序數(shù)的變化一定是奇數(shù)，最終狀態(tài)的逆序數(shù)15也是奇數(shù)，所以如果某個狀態(tài)逆序數(shù)和 0到目標點的曼哈頓距離
的奇偶性一致時，必定是無解的。