A. Up and Down
PKU 3912
http://poj.org/problem?id=3912
題意：給定一個一維的棋盤，范圍為[0, W] (W <= 1000,000,000)，某兩個點之間有梯子或蟲洞，梯子的下端點到上端點以及蟲洞的上端點到下端點花費的步數為0，其它任意點之間的距離通過跳躍來計算，最多每次跳躍不超過S格（S<= 6），跳躍的過程中如果跳到梯子的下端點或者蟲洞的上端點就會被直接傳送到另一端，并且每次跳躍只能從小的點跳到大的點（蟲洞是個例外），求從0到W的最短距離。
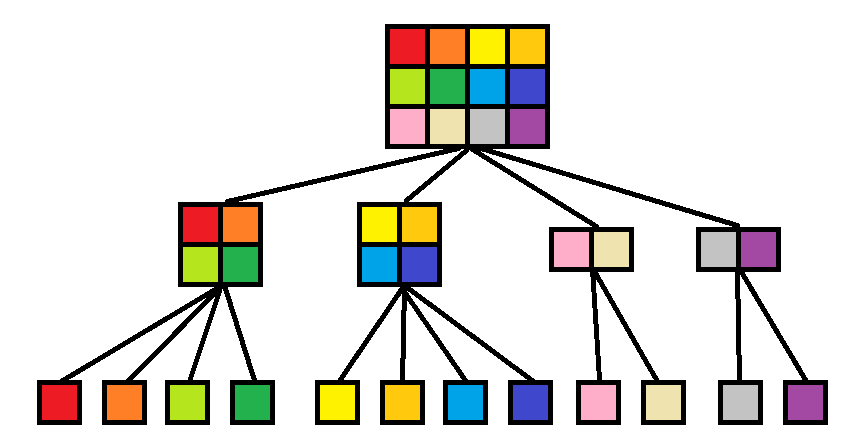
圖A-1
題解：
離散化 + SPFA。
將所有梯子和蟲洞的兩端點、0和W以及他們往前往后S步以內的數全部記錄下來，梯子和蟲洞有P（P <= 40）個，加上起點終點，總共82個點，算上前后各六步，總共82 * 13 = 1066個點，然后將這些點排序后離散化，最后就是要構建一個網絡圖，通過網絡求0到W的最短路，最短路可以用SPFA求解。
談談建圖的過程，對于任意兩個點，他們之間必定可以連一條邊，然后有一個步數表示邊的權值（這里的步數也可能是正無窮，也即永遠都無法到達）。
對于任意兩個點(u, v)，他們的步數w(u, v)（邊權）我們做如下討論（這里的u、v是離散化后的點）：
1）如果u是梯子的下端點，v是梯子的上端點 或者 u是蟲洞的上端點，v是蟲洞的下端點，那么w(u, v) = 0，否則進入2)的判斷;
2）如果u的編號大于v，w(u, v) = inf，表示永遠不可達，因為某次跳躍只能從小的點跳到大的點，否則進入3）的判斷;
3）如果u的實際位置和v的實際位置差值小于等于S，則w(u, v) = 1；
4）檢查u和v之間是否有蟲洞的上端點或者梯子的下端點，之后將這兩種點稱為X點
a）如果有，判斷他們是否連續，
i) 如果不連續w(u, v) = inf（這一步這么做是為了簡單化，試想一下，如果X點不是全部連續，說明u可以先跳到他們中間的某個非X的點，然后再跳到v點，這一步是通過SPFA來實現迭代的，建邊的時候可以不考慮）。
ii）如果連續，判斷他們連續的格子的數目，如果大于等于S說明這個連續的塊必定跳不過去，所以w(u, v) = inf，否則可以先跳到最先的一個X點的前面一個點，然后經過一步S跳躍將這個連續塊跳過去，再跳到v。
b）如果沒有X點，那么直接從u點跳到v點。
這里我們需要計算從a點跳到b點不考慮蟲洞和梯子的最短距離，可以貪心的跳，每次往大的跳，直到剩余格子不足S格，即(b-a + S-1) / S （b-a對S求商的上整）。
邊建立完成就可以利用廣搜求解0-W的最短路了。
B. Gnome Sequencing
PKU 3913 http://poj.org/problem?id=3913
水題，判斷三個數是全遞增還是全遞減還是無序。
C. DuLL
PKU 3914 http://poj.org/problem?id=3914
題意：給定一些dll文件和它占用的內存空間，以及一些可執行程序占用的內存空間和它依賴的dll文件，程序以進程為單位，兩個相同的程序可能有不同的進程，進行一些下列的操作：
1）某個程序運行的時候需要它依賴的dll文件也加載到內存中，多個程序可以共用一個dll文件；
2）某個程序退出的時候，如果它所依賴的dll文件沒有其它程序使用，需要釋放這段內存空間；
給定一系列的運行進程，求某個時刻的最大內存占用。
題解：HASH的簡單應用。
初始化內存占用V = 0，
對于給定的輸入進程：
1）如果是新運行的進程，將V加上這個進程的內存占用，并將它所有依賴的dll文件檢查一遍，如果引用計數為0，則將對應dll文件的內存累加到V上，引用計數+1；
2）如果是退出進程，將V減去這個進程的內存占用，并將它所有依賴的dll文件檢查一遍，如果引用計數為1，則用V減去對應dll文件的占用量，引用計數-1；
每次操作記錄最大的V就是最后的答案。
D. Black Vienna
PKU 3915 http://poj.org/problem?id=3915
題意：三個人，每個人五張牌，互相不知道對方的牌，還有額外的三張牌放在一邊（所有牌編號為A - R）。每一輪，由 (i-1)%3+1 (1 <= i <= 15) 號玩家進行發問，問Ai (1 <= Ai <= 3) 號玩家XYZ（代表任意三個牌號）三張牌中有多少張在他手上，然后他回答Bi (0 <= Bi <= 3)，問經過多少輪之后有某位玩家知道 額外 的那三張牌是什么。
題解：dfs枚舉 + 剪枝。
首先枚舉到某個詢問i的時候玩家j能夠猜出的那三張牌的情況，如果枚舉完所有情況最后確定只有一個解滿足條件的時候，那個詢問的編號i就是答案了。
類似IDA*的思路，先枚舉詢問最大深度，如果到達那個詢問不能確定額外的那三張牌或者有很多種情況，那么說明還需要更多的詢問，迭代深度繼續枚舉。
對于某個詢問i，找到詢問的那三張牌中已經是Ai號選手的數量ansCnt，以及尚未確定牌的歸屬的牌的數量xCnt，如果已經確定位置的牌數量 大于 實際他回答的數量（ansCnt > Bi）或者 尚未確定位置的牌數量 + 已經確定為他的牌數量 小于 實際他回答的數量（ansCnt + xCnt < Bi）都是不合理的情況，剪枝，不用繼續往下搜索；
否則，將(Bi - ansCnt)張牌分配給Ai，(xCnt - (Bi - ansCnt))張牌分配給其它兩位玩家以及額外的那一堆，這里需要用到嵌套dfs枚舉，枚舉完后進入下一個詢問的枚舉，每次詢問的時候可以有幾個剪枝：
1）如果某個階段某個人的牌數超過5張；
2）枚舉的解的數量超過2個；
3) 對于一次完全枚舉，枚舉完所有詢問后還是有無法確定三張額外的牌的情況；
E. Duplicate Removal
PKU 3916 http://poj.org/problem?id=3916
水題，對輸入的元素進行連續判重輸出。
F. Rock, Paper, Scissors
PKU 3917 http://poj.org/problem?id=3917
水題，剪刀石頭布！O_o
G. A to Z Numerals
PKU 3918 http://poj.org/problem?id=3918
題意：復雜模擬。（沒做出來，#-_-# 樣例的98是怎么出來的呀?。。。?/span>
H. Cell Towers
PKU 3919 http://poj.org/problem?id=3919
題意：給出一條曲折的連續線段，曲線從起點開始每經過一個長度為1的單位會放置一個守衛K，在曲線以外的某些地方會有T(T <= 10)個信號發射器，用A、B、C...來表示，每個信號發射器有它的信號強度Pi，每個信號發射器到守衛K的距離如果是D，那么它能接收到的信號值為Pi / D2的最近整數，并且對于守衛K，它只會接收最大的信號值，如果有多個發射器對于K的信號值相同，那么選擇字典序最小的發射器。需要求是一些守衛集合，這些守衛分別和它的前一個守衛所接收的信號發射器不一樣。
題解：計算幾何、向量的簡單應用。
對于每條射線，終點減去起點，再單位化后就可以得到這條射線的單位向量，利用這一點可以很簡單的將所有守衛的坐標求出來，然后對于每個守衛判斷接收的是哪個發射器，判斷和之前那個守衛是否相同即可。
需要注意的是最后一個守衛，當和上一個守衛距離小于0.5的時候不會建立新的守衛。
I. RIPOFF
PKU 3920 http://poj.org/problem?id=3920
題意：給定N(N <= 200)個數的一維數組A，取不大于T+2個數，每相鄰兩個數之間的下標不大于S，問最大的取值總和(第0個和第N+1個數必取，且權值為0)。
題解：動態規劃。
DP[i][j] 表示第j個數取 A[i]的最大值，那么狀態轉移方程可以表示為：
DP[i][j] = max{ DP[k][j-1] + A[i], i > k > i-1-S && k >= 0};
特殊的，DP[0][0] = 0，其他的DP[i][j] 都初始化為INF;
最后計算出的DP[N+1][i]中的最大值就是答案了。