英雄哪里出來(lái)

       計(jì)算幾何：射線旋轉(zhuǎn)

       題意：需要求一個(gè)正多邊形的N個(gè)點(diǎn)，但是給出的只有N和某兩個(gè)點(diǎn)的坐標(biāo)。

       題解：核心思想是根據(jù)給定的那兩個(gè)點(diǎn)的坐標(biāo)確定多邊形中心點(diǎn)的坐標(biāo)，這樣邊長(zhǎng)也確定了，然后利用中心點(diǎn)到其中一個(gè)點(diǎn)的射線的旋轉(zhuǎn)求出所有的點(diǎn)坐標(biāo)。

       1) 正多邊形的中心點(diǎn)一定在任意兩個(gè)頂點(diǎn)的連線的中垂線上，然后根據(jù)已知點(diǎn)的相對(duì)關(guān)系，算出他們和中心點(diǎn)的夾角，利用這兩個(gè)條件就可以求出中心點(diǎn)的坐標(biāo)了。

       2) 然后就是要求某個(gè)點(diǎn)繞中心點(diǎn)旋轉(zhuǎn)360/N度后的坐標(biāo)了，做N-1次旋轉(zhuǎn)操作就能求出所有的頂點(diǎn)了。旋轉(zhuǎn)可以通過解方程求解：

       令原單位向量I，旋轉(zhuǎn)alpha角度后的單位向量I_a，其中I和alpha已知，I_x是我們需要求的。那么有以下兩個(gè)方程：

       1) I.x * I_a.x + I.y * I_a.y = cos( alpha )

       2) I_a.x² + I_a.y² = 1

       將1)中的I_a.x用I_a.y表示代入方程2)，利用一元二次求根公式可以求得兩個(gè)解，然后算出I_a.x，但是解肯定只有一個(gè)，可以用叉乘關(guān)系排除掉另外一個(gè)解。

121 Bridges painting

      圖論：DFS構(gòu)造

題意：對(duì)于一個(gè)圖，給定它的邊和點(diǎn)，現(xiàn)在要求給邊染色（黑色或者白色）。問能不能構(gòu)造一種染色方法，使得所有的度數(shù)大于1的點(diǎn)的邊都能有至少有一條邊為黑色、至少有一條邊為白色。

題解：首先考慮什么情況下是不可能染色成功的；如圖1所示，對(duì)于下面這個(gè)圖，每個(gè)點(diǎn)的頂點(diǎn)度數(shù)為2，所以從任意一條邊開始染色，相鄰邊必然為相反色，由于存在奇環(huán)，導(dǎo)致必然有一個(gè)點(diǎn)的兩條邊的顏色相同，染色失敗。

然后再來(lái)考慮怎么將這個(gè)圖挽救回來(lái)，其實(shí)這個(gè)圖失敗的點(diǎn)只有一個(gè)，如果在那個(gè)點(diǎn)上再加一條邊，那么整個(gè)圖貌似就可以認(rèn)為染色成功了。

于是我們進(jìn)一步考慮是不是度數(shù)為奇數(shù)的點(diǎn)造就了這一切：

度數(shù) = 1，該點(diǎn)所在邊可以隨便染色；

度數(shù) > 1，說明必然存在環(huán)；

如果是偶數(shù)環(huán)，那么經(jīng)過一系列的交錯(cuò)染色，最后必然能夠在該結(jié)點(diǎn)上收獲兩條顏色不一樣的邊；

如果是奇數(shù)環(huán)，在染色完畢后，必然還有一條邊未被染色（因?yàn)槎葦?shù)為奇數(shù)），可以大膽的將它染成不同的顏色；

所以對(duì)于度數(shù)為奇數(shù)的點(diǎn)，采用交錯(cuò)染色，一定可以將圖染色成功；

如圖，可以對(duì)于所有奇度數(shù)頂點(diǎn)作為根進(jìn)行一次dfs，按照編號(hào)順序進(jìn)行深度優(yōu)先遍歷，先遍歷到的是1號(hào)，標(biāo)記為黑色，然后將它的第一個(gè)兒子標(biāo)記為白色，遍歷完畢，將第二個(gè)兒子標(biāo)記為黑色（交錯(cuò)染色），即每次更換結(jié)點(diǎn)的時(shí)候就將顏色取反，當(dāng)我們遍歷到邊6的時(shí)候發(fā)現(xiàn)7是一條后向邊，于是回到了根結(jié)點(diǎn)，完成遍歷。

利用同樣方法，將所有度數(shù)為奇數(shù)的點(diǎn)進(jìn)行一次遍歷，然后再將度數(shù)為偶數(shù)的點(diǎn)進(jìn)行相同的遍歷（因?yàn)榭赡苓@不是一個(gè)連通圖，所以如果度數(shù)為偶數(shù)的點(diǎn)所在的圖集合中有奇數(shù)環(huán)，如圖1的情況，那么必然無(wú)解）。

遍歷完畢，需要對(duì)每個(gè)點(diǎn)判斷是否存在不合法的頂點(diǎn)（邊數(shù)大于1，并且只有一種染色），如果合法，說明所有邊都被染色了，輸出解即可。

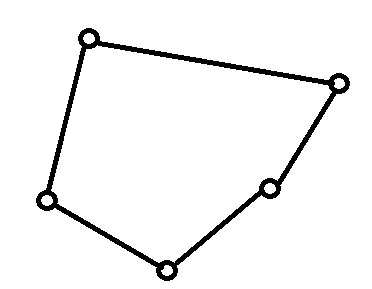
圖1

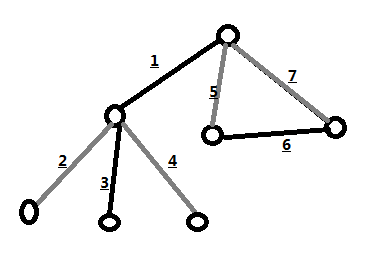
圖2

122 The book

      哈密爾頓回路問題：Ore定理 + 構(gòu)造

題意：給定N(N <= 1000)個(gè)點(diǎn)連成的圖，每個(gè)點(diǎn)度數(shù)大于等于(N+1)/2，求這個(gè)圖的一條哈密爾頓回路。

題解：

1）首先假設(shè)已經(jīng)得到了一個(gè)環(huán)R（R的頂點(diǎn)個(gè)數(shù)為r），那么在未選到環(huán)內(nèi)的點(diǎn)集R’中必然能夠找到某個(gè)點(diǎn)k和環(huán)R中其中一個(gè)點(diǎn)j有邊相連，假設(shè)沒有邊相連，那么環(huán)R和環(huán)外的點(diǎn)集R’互不連通，為兩個(gè)連通分量，和題意相左（因?yàn)槊總€(gè)點(diǎn)的度數(shù)大于等于（N+1）/2，圖論書上有證明，這肯定是一個(gè)連通圖，故不再累述），故R’中必然存在至少一個(gè)點(diǎn)k和R中點(diǎn)j相連，于是將那個(gè)點(diǎn)j連接到k上，這樣就變成了一個(gè)長(zhǎng)度為r+1的鏈。

2）這個(gè)鏈的頭為s，尾為k，長(zhǎng)度為r+1，不斷在剩下的點(diǎn)集中找點(diǎn)連接到s和k上，并且不斷更新s和k（連接到頭上，連接的點(diǎn)就變成了s，連接到尾上，連接的點(diǎn)就變成了k），直到找到一個(gè)極大連通子鏈（不能再在剩下的點(diǎn)中找到點(diǎn)連接到鏈的兩端了）。

3）由于k和剩下點(diǎn)集R’沒有點(diǎn)相連，所以我們只能在這條長(zhǎng)鏈上找和k相連的點(diǎn)t（因?yàn)橐欢梢哉业剑瑸槭裁茨兀?/span>k本身不就有個(gè)鏈內(nèi)的點(diǎn)連著嘛，不然它就是個(gè)孤立點(diǎn)了）。所以找到(k , t)相連，并且(s, t+1) 相連，然后刪掉(t, t+1)這條邊，就能夠得到一個(gè)新的環(huán)了，如果此時(shí)環(huán)的長(zhǎng)度為n就結(jié)束了，否則繼續(xù)1）。

 

圖3

123 The sum

      遞推

       題意：求斐波那契數(shù)列的第N(N <= 40)項(xiàng)。

       題解：__int64數(shù)組預(yù)處理即可。

124 Broken line

      計(jì)算幾何: 線段判交

       題意：在平面上有一些閉合線段（沒有自交和相互交叉），判斷給定的點(diǎn)P是否在這個(gè)閉合線段內(nèi)。

       題解：其實(shí)就是判斷一個(gè)點(diǎn)是否在多邊形內(nèi)；

       首先，虛擬出一個(gè)無(wú)窮遠(yuǎn)的點(diǎn)Q，然后用PQ和每個(gè)閉合線段去做相交檢測(cè)(兩線段判交在黑書上有詳盡的解釋,不再累述)。

       1) 如果P在某條線段上，輸出BORDER；

       2) 如果PQ和所有線段交點(diǎn)個(gè)數(shù)為奇數(shù)，說明在多邊形內(nèi)，輸出INSIDE；

       3) 如果PQ和所有線段交點(diǎn)個(gè)數(shù)為偶數(shù)，說明在多邊形外，輸出OUTSIDE；

 

125 Shtirlits

      深度優(yōu)先搜索 + 剪枝

       題意：給定一個(gè)矩陣B (3X3)，B[i][j]表示A[i][j]四周比它大的數(shù)的個(gè)數(shù)，求滿足條件的A。

       題解：枚舉A[i][j]的每個(gè)數(shù)字，數(shù)字的范圍為 [0,9]。復(fù)雜度10⁹，所以需要進(jìn)行一定的剪枝。

       a)   首先，可以肯定這B[i][j]中一定會(huì)至少有一個(gè)0，因?yàn)榭傆幸粋€(gè)數(shù)沒有比它大的數(shù)（高處不勝寒啊~~）。對(duì)于B[i][j] == 0的格子，將A[i][j]設(shè)為最大值9一定不會(huì)錯(cuò)，所以復(fù)雜度至少可以降到 10⁸ 了。

       b)   將A的每個(gè)非9的格子標(biāo)記為-1，然后對(duì)每個(gè)格子進(jìn)行枚舉，枚舉范圍為 [ 0, 8 ], 因?yàn)?/span>B[i][j]為四周比它大的數(shù)的個(gè)數(shù), 如果A[i][j]==9，那么B[i][j]必須為0，復(fù)雜度降至 9⁸。

       c)   每次枚舉完畢，進(jìn)入下一個(gè)數(shù)的枚舉之前，進(jìn)行全局的檢測(cè)，對(duì)于每個(gè)格子統(tǒng)計(jì)以下數(shù)據(jù)：

            i)    已經(jīng)枚舉的鄰居格子      H

            ii)   總共有多少個(gè)鄰居格子   T

             iii)   比自己大的鄰居格子       B

     然后進(jìn)行篩選，如果

          x) 比當(dāng)前格子大的鄰居數(shù)已經(jīng)超出限定值, 即 B > B[i][j]

          y) 比當(dāng)前格子大的鄰居數(shù) + 剩余未知鄰居數(shù) < 給定比它大的鄰居數(shù)， 即 B + (T-H) < B[i][j]

     均為無(wú)效解，無(wú)需往下枚舉，回溯。

       d)   直到所有數(shù)枚舉完畢，輸出解即可。

126 Boxes

      初等數(shù)論

       題意：對(duì)于給定的A和B，

              如果A > B, 則狀態(tài)變?yōu)?/span> (A-B, 2*B)

              如果A < B, 則狀態(tài)變?yōu)?/span> (2*A, B-A)

              當(dāng) A == B 時(shí)，結(jié)束。

              要求輸出這個(gè)情況是否存在，如果存在輸出變換的次數(shù)，不存在輸出-1。

       題解：根據(jù)題意，可以得出一些簡(jiǎn)單的推論：

          a) 當(dāng)A == 0 或者 B == 0 時(shí) 答案為 0。

          b) 最后A == B的時(shí)候，必定是K = (A+B)/2，所以當(dāng)A+B為奇數(shù)時(shí)答案不存在。

          c) 定義最后的狀態(tài)二元組為 (K, K),

                倒數(shù)第二次的操作必定為 (3K/2,K/2)  或者(K/2,3K/2)                                                                                                 (2種)

                倒數(shù)第三次的操作必定為 (7K/4, K/4) 或者 (3K/4, 5K/4) 或者 (5K/4, 3K/4) 或者 (K/4, 7K/4)                                         (4種)

                倒數(shù)第四次操作(15K/8,K/8)...                                                                                                                                   (8種)

                倒數(shù)第i次操作 ( (2^(i-1)-1)/2^(i-1) * K, 1/2^(i-1) * K ) ...                                                                                                    (2^(i-1) 種)

          d) A和B的組合必定在這些情況中找。

              于是定義 A = L1 / 2ⁿ * K,  B = L2 / 2ⁿ * K  (其中K = (A+B)/2, L1,L2為奇數(shù)，并且(L1+L2) = 2⁽ⁿ⁺¹⁾)

             得：

                 L1 = 2ⁿ * (A/K)

                 L2 = 2ⁿ * (B/K)

        令 A = 2^a * A', K = 2^k * K'

        則有 L1 = 2^(n+a-k) * A'/K' 為奇數(shù)，所以n+a-k = 0，并且要保證A' mod K' == 0，A 和 K 都為已知，則可以計(jì)算出 a 、A'、k、K'，最終的步數(shù)就是k-a+1。

        需要注意特殊情況：A或B為0的情況，以及A+B為奇數(shù)的情況。

127 Telephone directory

      將所有電話號(hào)碼按首字母排序，統(tǒng)計(jì)每個(gè)首字母出現(xiàn)的次數(shù)Ai， Sum{ (Ai + K - 1 ) / K } + 2 就是答案。

128 Snake

       想法題

       題意：給定N（4<=N<=10000）個(gè)整數(shù)點(diǎn)，問能不能組出一個(gè)多邊形，滿足以下條件：

       a) 閉合；

       b) 所有的點(diǎn)都是多邊形上的點(diǎn)，并且只能被用一次；

       c) 任何兩個(gè)連續(xù)的線段需要組成一個(gè)90度的直角；

       d) 多邊形的所有邊都要平行于坐標(biāo)軸；

       e) 多邊形不能存在自交；

       f) 多邊形的周長(zhǎng)要滿足最小；

       題解：

       1) 對(duì)于輸入的點(diǎn)保存兩份數(shù)組PX、PY，并且記錄每個(gè)點(diǎn)在原數(shù)組的下標(biāo)index；

       2) 對(duì)PX進(jìn)行X優(yōu)先排序，對(duì)PY進(jìn)行Y優(yōu)先排序；

       3) 對(duì)PX中序號(hào)為奇數(shù)的點(diǎn)PX[i]和它的下一個(gè)點(diǎn)PX[i+1]進(jìn)行y值的判斷，如果這兩個(gè)點(diǎn)的y值不相等，那么說明這個(gè)點(diǎn)無(wú)法加入多邊形中（PX[i]無(wú)法配對(duì)，被孤立了），無(wú)解。否則PX[i].index和PX[i+1].index必然有一條邊（可以用鄰接表來(lái)存邊關(guān)系，因?yàn)樽詈笄蟮氖且粋€(gè)多邊形，所以每個(gè)點(diǎn)有且僅有兩條邊，其實(shí)就是一個(gè)哈密爾頓回路）。

          并且加PX[i+1].x - PX[i].index 累加到答案ans中；

       4) 對(duì)PY中的點(diǎn)作和3）一樣的處理，保存邊的關(guān)系，但是這里需要判斷一種自交的情況，如圖1中，3)操作完畢后，產(chǎn)生三條邊(1,1) - (2,1)  (1,2) -(3, 2)   (2,3) - (3,3)；那么在進(jìn)行操作4）的時(shí)候(1,1)-(1,2) 和 (3,2) - (3, 3)都是沒問題的，唯獨(dú) (2,1) - (2,3) 和 先前的邊 (1,2) -(3, 2) 會(huì)產(chǎn)生自交，違反了e這條規(guī)則，所以需要檢測(cè)這種情況是否存在，如果存在，那么必然無(wú)解；具體檢測(cè)方法很多，不再累述；

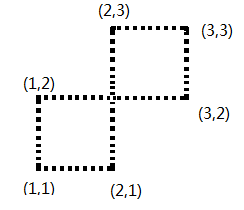
圖1

       5) 進(jìn)過3)和4)后，再進(jìn)行一次連通性判斷即可，以防圖2的情況。

圖2

129 Inheritance

      解析幾何 + 凸包 + 線段判交

         題意：給定一個(gè)多邊形和若干線段，這個(gè)多邊形內(nèi)任意兩點(diǎn)連線不會(huì)和多邊形邊界相交，分別求這些線段在多邊形內(nèi)部的長(zhǎng)度。

         題解：首先，根據(jù)“多邊形內(nèi)任意兩點(diǎn)連線不會(huì)和多邊形邊界相交”可以肯定這是個(gè)凸多邊形，于是問題就轉(zhuǎn)化成了求某條線段和凸多邊形相交后線段在多邊形內(nèi)部分的長(zhǎng)度。

         由于給定的點(diǎn)是亂序的，所以最簡(jiǎn)單的方法是求這些點(diǎn)集的一個(gè)凸包，構(gòu)造出一個(gè)按點(diǎn)排序的多邊形，相鄰兩點(diǎn)連線為原多邊形的一條邊。

那么枚舉每條邊和給定線段的相交情況：

         1) 不相交（平行），繼續(xù)判斷下一條邊；

         2) 共線，直接跳出枚舉，（由于是凸多邊形，改線段肯定不可能在多邊形內(nèi)）；

         3) 相交，將這個(gè)交點(diǎn)存入集合S；

         將原線段的兩個(gè)端點(diǎn)存入集合S，對(duì)集合S的點(diǎn)進(jìn)行x坐標(biāo)遞增排序（x相同時(shí)y坐標(biāo)遞增排序），然后枚舉相鄰兩個(gè)點(diǎn)的中點(diǎn)，判斷是否在在原多邊形內(nèi)，如果在，那么將這兩個(gè)相鄰點(diǎn)練成的線段的長(zhǎng)度累加到最后的答案中。如圖1為兩個(gè)交點(diǎn)的情況。

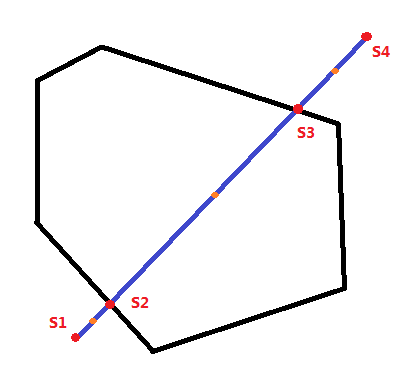
圖1