有一段輸入的離散信號{Zi},假定這段信號長度為N(N=2^n)。
Q1:
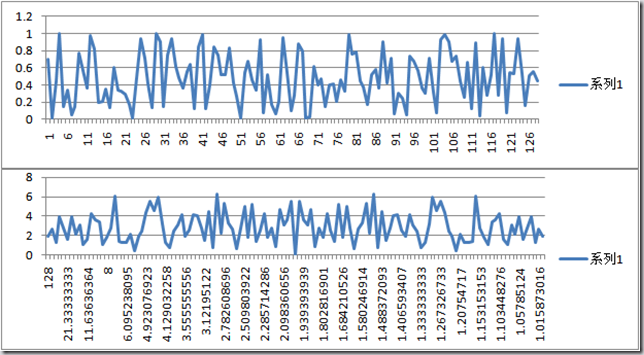
通常,可以用Fourier Transform來進(jìn)行頻域分析。例如對于一段隨機(jī)白噪,可以得出時(shí)域和頻域的圖像如下:
其中,上圖為時(shí)域,橫軸t,縱軸為Zt。下圖為頻域,橫軸為1/f(即周期T),縱軸為|Fn|(波幅)。
如果有這樣一種假說,一個(gè)信號,是由一個(gè)基頻與若干高/低頻諧波和噪聲的混合,且基頻、噪聲和高/低頻諧波的波幅存在著一定的分布率,例如指數(shù)分布,例如,假設(shè)基頻波幅期望是t(0<t<1),而次一級的諧波/噪聲波幅的期望為t^2,以此類推。且信號的波幅是隨機(jī)的,其波幅概率曲線成正態(tài)分布。
問題:有沒有一種辦法,可以對頻譜加以分析,判斷出可能概率最大的基頻頻率,并給出這一判斷的概率是多少。(要做假設(shè)檢驗(yàn)用,例如90%)
Q2:
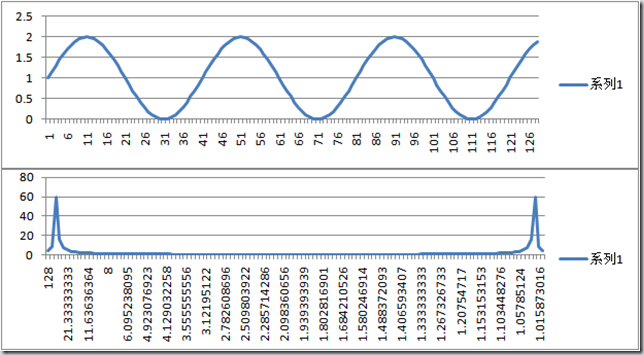
使用一個(gè)信號發(fā)生器,Zi = 1 + Sin( i * Pi / 20 )。并經(jīng)過傅里葉分析,得出以下的時(shí)域和頻域統(tǒng)計(jì):
其中,上圖為時(shí)域,橫軸t,縱軸為Zt。下圖為頻域,橫軸為1/f(即周期T),縱軸為|Fn|(波幅)。
問題:為什么在周期接近1的時(shí)候,會有一個(gè)波幅尖峰?