先來段前言。

今天跟某vczh在群里面聊天的時(shí)候，他突然很詭秘的說要我看看他的空間連接。
然后翻開一看，我靠，一連串1-7的標(biāo)題。
從尾到頭倒讀一通，才發(fā)現(xiàn)寫的挺清楚的，比一般的教科書都要到位。
不愧是要去google/msra實(shí)習(xí)的編譯器狂人。（此人成天琢磨編譯器）
遂轉(zhuǎn)發(fā)，希望對有志了解編譯器工作原理的人們有所幫助。
雖然這小子說不能修改，但是有的玩意貼的時(shí)候還是稍微動一下好發(fā)一點(diǎn)。
不跟他打招呼了，嘿嘿。

構(gòu)造可配置詞法分析

陳梓瀚
華南理工大學(xué)計(jì)算機(jī)軟件學(xué)院軟件工程05級本科
vczh _at_ 163 _dot_ com
2007-11-8

 

    本文詳細(xì)描述了通過正則表達(dá)式構(gòu)造通用詞法分析器的整個(gè)算法流程。如果有需要的話請?jiān)谠u論留下自己的Email，或通過QQ向本人索取文章及附件。任何人(除了作者)不得修改本文。自由轉(zhuǎn)載，注明出處。

    文檔使用doc格式。附件帶有文章所有圖片的jpg及vsd格式。

構(gòu)造可配置詞法分析器

 

陳梓瀚

華南理工大學(xué)計(jì)算機(jī)軟件學(xué)院軟件工程05級本科

vczh@163.com

2007-11-8

 

一、問題概述

 

隨著計(jì)算機(jī)語言的結(jié)構(gòu)越來越復(fù)雜，為了開發(fā)優(yōu)秀的編譯器，人們已經(jīng)漸漸感到將詞法分析獨(dú)立出來做研究的重要性。不過詞法分析器的作用卻不限于此。回想一下我們的老師剛剛開始向我們講述程序設(shè)計(jì)的時(shí)候，總是會出一道題目：給出一個(gè)填入了四則運(yùn)算式子的字符串，寫程序計(jì)算該式子的結(jié)果。除此之外，我們有時(shí)候建立了比較復(fù)雜的配置文件，譬如XML的時(shí)候，分析器首先也要對該文件進(jìn)行詞法分析，把整個(gè)字符串?dāng)喑闪艘粋€(gè)一個(gè)比較短小的記號(指的是具有某種屬性的字符串)，之后才進(jìn)行結(jié)構(gòu)上的分析。再者，在實(shí)現(xiàn)某種控制臺應(yīng)用程序的時(shí)候，程序需要分析用戶打進(jìn)屏幕的命令。如果該命令足夠復(fù)雜的話，我們也首先要對這個(gè)命令進(jìn)行詞法分析，之后得到的結(jié)果會大大方便進(jìn)行接下去的工作。

 

當(dāng)然，這些問題大部分已經(jīng)得到了解決，而且歷史上也有人做出了各種各樣專門的或者通用的工具(Lex、正則表達(dá)式引擎等)來解決這一類問題。我們在使用這種工具的時(shí)候，為了更加高效地書寫配置，或者我們在某種特殊情況下需要自己制作類似的工具，就需要了解詞法分析背后的原理。本文將給出一個(gè)構(gòu)造通用詞法分析工具所需要的原理。由于實(shí)現(xiàn)的代碼過長，本文將不附帶實(shí)現(xiàn)。

 

究竟什么是“把一個(gè)字符串?dāng)喑梢恍┯浱?#8221;呢？我們先從四則運(yùn)算式子入手。一個(gè)四則運(yùn)算式子是一個(gè)字符數(shù)列，可是我們關(guān)心的對象實(shí)際上是操作符、括號和數(shù)字。于是此法分析的作用就是把一個(gè)字符串?dāng)嚅_成我們關(guān)心的帶有屬性的記號。舉個(gè)例子：(11+22)*(33+44)是一個(gè)合法的四則運(yùn)算式子，如果輸入是(左括號,”(“) (數(shù)字,”11”) (一級操作符,”+”) (數(shù)字,”22”) (右括號,”)”) (二級操作符,”*”) (左括號,”(“) (數(shù)字,”33”) (一級操作符,”+”) (數(shù)字,”44”) (右括號,”)”)的話，我們在檢查結(jié)構(gòu)的時(shí)候只需要關(guān)心這個(gè)記號的屬性(也就是左括號、右括號、數(shù)字、操作符等)就行了，具體計(jì)算的時(shí)候才需要關(guān)心這個(gè)記號實(shí)際上的內(nèi)容。如果式子里邊有空格的話，我們也僅僅需要把空格當(dāng)成是一種記號類型，在詞法分析得出結(jié)果之后，將具有空格屬性的記號丟棄掉就可以了，接下去的步驟不需變化。

 

但需要注意的是，詞法分析得到的結(jié)果是沒有層次結(jié)構(gòu)的，所有的記號都是等價(jià)的對象。我們在計(jì)算表達(dá)式的時(shí)候把+和*看成了不同層次的操作符，類似的結(jié)構(gòu)是具有嵌套的層次的。詞法分析不能得出嵌套層次結(jié)構(gòu)的信息，最多只能得到關(guān)于重復(fù)結(jié)構(gòu)的信息。

 

二、正則表達(dá)式

 

我們現(xiàn)在需要尋找一種可以描述記號類型的工具，在此之前我們首先研究一下常見的記號的結(jié)構(gòu)。為了表示出具有某種共性的字符串的集合，我們需要書寫出一些能代表字符串集合的規(guī)則。這個(gè)集合中的所有成員都將被認(rèn)為是一種特定類型的記號。

 

首先，規(guī)則可以把一個(gè)特定的字符或者是空字符串認(rèn)為是一種類型的記號的全部。上文所說到的四則運(yùn)算式子的例子，“左括號”這種類型的記號就僅僅對應(yīng)著字符”(“，其他的字符或者字符串都不可能是“左括號”這個(gè)類型的記號。

 

其次，規(guī)則可以進(jìn)行串聯(lián)。串聯(lián)的意思是這樣的，我們可以讓一個(gè)字符串的前綴符合某一個(gè)指定的規(guī)則，剩下的部分的前綴符合第二個(gè)規(guī)則，剩下的部分的前綴符合第三個(gè)規(guī)則等等，一直到最后一個(gè)部分的全部要符合最后一個(gè)規(guī)則。如果我們把”function”這個(gè)字符串作為一個(gè)記號類型來處理的話，我們可以把”function”這個(gè)字符串替換成8個(gè)串聯(lián)的規(guī)則：”f”,”u”,”n”,”c”,”t”,”i”,”o”,”n”。首先，字符串”function”的前綴”f”符合規(guī)則”f”，剩下的部分”unction”的前綴”u”符合規(guī)則”u”，等等，一直到最后一個(gè)部分”n”的全部符合規(guī)則”n”。

 

第三，規(guī)則可以進(jìn)行并聯(lián)。并聯(lián)的意思就是，如果一個(gè)字符串符合一系列規(guī)則中的其中一個(gè)的話，我們就說這個(gè)字符串符合這一些規(guī)則的并聯(lián)。于是這些規(guī)則的并聯(lián)就構(gòu)成了一個(gè)新的規(guī)則。一個(gè)典型的例子就是判斷一個(gè)字符串是否關(guān)鍵字。關(guān)鍵字可以是”if”，可以是”else”，可以是”while”等等。當(dāng)然，一個(gè)關(guān)鍵字是不可能同時(shí)符合這些規(guī)則的，不過只要一個(gè)字符串符合這些規(guī)則的其中一個(gè)的話，我們就說這個(gè)字符串是關(guān)鍵字。于是，關(guān)鍵字這個(gè)規(guī)則就是”if”、”else”、”while”等規(guī)則的并聯(lián)。

 

第四，一個(gè)規(guī)則可以是可選的。可選的規(guī)則實(shí)際上是屬于并聯(lián)的一種特殊形式。加入我們需要規(guī)則”abc”和”abcde”并聯(lián)，我們會發(fā)現(xiàn)這兩個(gè)規(guī)則有著相同的前綴”abc”，而且這個(gè)前綴恰好就是其中的一個(gè)規(guī)則。于是我們可以把規(guī)則改寫成”abc”與””和”de”的并聯(lián)的串聯(lián)。但是規(guī)則””指定的規(guī)則是空串，因此這個(gè)規(guī)則與”de”的并聯(lián)就可以看成是一個(gè)可選的規(guī)則”de”。

 

第五，規(guī)則可以被重復(fù)。有限次的重復(fù)可以使用串聯(lián)表示，但是如果我們不想限制重復(fù)的次數(shù)的話，串聯(lián)就沒法表示這個(gè)規(guī)則了，于是我們引入了“重復(fù)”。一個(gè)典型的例子就是程序設(shè)計(jì)語言的標(biāo)識符。標(biāo)識符可以是一個(gè)變量的名字或者是其他東西。一門語言通常沒有規(guī)定變量名的最大長度。因此為了表示這個(gè)規(guī)則，就需要將52個(gè)字母進(jìn)行并聯(lián)，然后對這個(gè)規(guī)則進(jìn)行重復(fù)。

 

上述的5種構(gòu)造規(guī)則的方法中，后面的4個(gè)方法被用于把規(guī)則組合成為更大的規(guī)則。為了給出這種規(guī)則的形式化表示，我們引入了一種范式。這種范式有以下語法：

1：字符用雙引號包圍起來，空串使用ε代替。

2：兩個(gè)規(guī)則頭尾連接代表規(guī)則的串聯(lián)。

3：兩個(gè)規(guī)則使用 | 隔開代表規(guī)則的并聯(lián)。

4：規(guī)則使用[]包圍代表該規(guī)則是可選的，規(guī)則使用{}包圍代表該規(guī)則是重復(fù)的。

5：規(guī)則使用()包圍代表該規(guī)則是一個(gè)整體，通常用于改變操作符 | 的優(yōu)先級。

 

舉個(gè)例子，一個(gè)實(shí)數(shù)的規(guī)則書寫如下：

{“0”|”1”|”2”|”3”|”4”|”5”|”6”|”7”|”8”|”9”}”.”[{“0”|”1”|”2”|”3”|”4”|”5”|”6”|”7”|”8”|”9”}]。

 

但是，我們?nèi)绾伪硎?#8220;不是數(shù)字的其他字符呢”？字符的數(shù)量是有限的，因此我們可以使用規(guī)則的并聯(lián)來表示。但是所有的字符實(shí)在是太多（ASCII字符集有127個(gè)字符，UTF-16字符集有65535個(gè)字符），因此后來人們想出了各種各樣的簡化規(guī)則書寫的辦法。比較著名的有BNF范式。BNF范式經(jīng)常被用于理論研究，但是更加實(shí)用的是正則表達(dá)式。

 

正則表達(dá)式的字符不需要用雙引號括起來，但是如果需要表示一些被定義了的字符(如 “|” )的話，就使用轉(zhuǎn)義字符的方法表示(如 “\|”)。其次，X?代表[X]，X+代表{X}，X*代表[{X}]。字符集合可以用區(qū)間來表示，[0-9]可以表示“0”|”1”|”2”|”3”|”4”|”5”|”6”|”7”|”8”|”9”，[^0-9]則表示“除了數(shù)字以外的其他字符”。正則表達(dá)式還有各種各樣的其他規(guī)則來簡化我們的書寫，不過由于本文并不是“精通正則表達(dá)式”，因此我們只保留若干比較本質(zhì)的操作來進(jìn)行詞法分析原理的描述。

 

正則表達(dá)式的表達(dá)能力極強(qiáng)，小數(shù)的規(guī)則可以使用[0-9]+.[0-9]來表示，C語言的注釋可以表示為/\*([^\*]|\*+[\*/])*\*+/來表示。

 

三、有窮狀態(tài)自動機(jī)

 

人閱讀正則表達(dá)式會比較簡單，但是機(jī)器閱讀正則表達(dá)式就是一件非常困難的事情了。而且，直接使用正則表達(dá)式進(jìn)行匹配配的話，不僅工作量大，而且速度緩慢。因此我們還需要另外一種專門為機(jī)器設(shè)計(jì)的表達(dá)方式。本文在以后的章節(jié)中會給出一種算法把正則表達(dá)式轉(zhuǎn)換為機(jī)器可以閱讀的形式，就是這一章節(jié)所描述的有窮狀態(tài)自動機(jī)。

 

有窮狀態(tài)自動機(jī)這個(gè)名字聽起來比較可怕，不過實(shí)際上這種自動機(jī)并沒有想象中的那么復(fù)雜。狀態(tài)機(jī)的這種概念被廣泛的應(yīng)用在各種各樣的領(lǐng)域中。軟件工程的統(tǒng)一建模語言(UML)有狀態(tài)圖，數(shù)字邏輯中也有狀態(tài)轉(zhuǎn)移圖。不過這些各種各樣的圖在本質(zhì)上都跟狀態(tài)機(jī)沒有什么區(qū)別。我將會通過一個(gè)例子來講述狀態(tài)的實(shí)際意義。

 

假設(shè)我們現(xiàn)在需要檢查一個(gè)字符串中a的數(shù)量和b的數(shù)量是否都是偶數(shù)。當(dāng)然我們可以用一個(gè)正則表達(dá)式來描述它。不過對于這個(gè)問題來說，用正則表達(dá)式來描述遠(yuǎn)遠(yuǎn)不如構(gòu)造狀態(tài)機(jī)方便。我們可以設(shè)計(jì)出一個(gè)狀態(tài)的集合，然后指定集合中的某一個(gè)元素為“起始狀態(tài)”。其實(shí)狀態(tài)就是在工作還沒開始的時(shí)候，分析器所處的狀態(tài)。分析器在每一次進(jìn)行一項(xiàng)新的工作的時(shí)候，都要把狀態(tài)重置為起始狀態(tài)。分析器每讀入一個(gè)字符就修改一次狀態(tài)，修改的方法我們也可以指定。分析器在讀完所有的字符以后，必然停留在一個(gè)確定的狀態(tài)中。如果這個(gè)狀態(tài)跟我們所期望的狀態(tài)一致的話，我們就說這個(gè)分析器接受了這個(gè)字符串，否則我們就說這個(gè)分析器拒絕了這個(gè)字符串。

 

如何通過設(shè)計(jì)狀態(tài)及其轉(zhuǎn)移方法來實(shí)現(xiàn)一個(gè)分析器呢？當(dāng)然，如果一個(gè)字符串僅僅包含a或者b的話，那么分析器的狀態(tài)只有四種：“奇數(shù)a奇數(shù)b”、“奇數(shù)a偶數(shù)b”、“偶數(shù)a奇數(shù)b”、“偶數(shù)a偶數(shù) b”。我們把這些狀態(tài)依次命名為aa、aB、Ab、AB。大寫代表偶數(shù)，小寫代表奇數(shù)。當(dāng)工作還沒開始的時(shí)候，分析器已經(jīng)讀入的字符串是空串，那么理所當(dāng)然的起始狀態(tài)應(yīng)當(dāng)是AB。當(dāng)分析器讀完所有字符的時(shí)候，我們期望讀入的字符串的a和b的數(shù)量都是偶數(shù)，那么結(jié)束的狀態(tài)也應(yīng)該是AB。于是我們給出這樣的一個(gè)狀態(tài)圖：

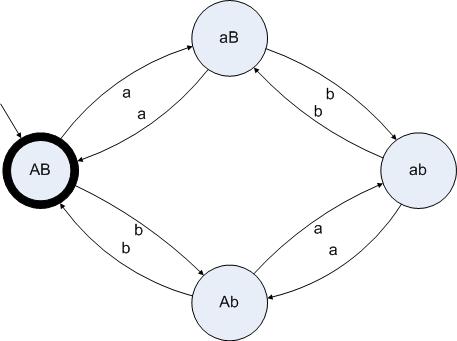
圖3.1

檢查一個(gè)字符串是否由偶數(shù)個(gè)a和偶數(shù)個(gè)b組成的狀態(tài)圖

 

在這個(gè)狀態(tài)圖里，有一個(gè)短小的箭頭指向了AB，代表AB這個(gè)狀態(tài)是初始狀態(tài)。AB狀態(tài)有粗的邊緣，代表AB這個(gè)狀態(tài)是結(jié)束的可接受狀態(tài)。一個(gè)狀態(tài)圖的結(jié)束狀態(tài)可以是一個(gè)或者多個(gè)。在這個(gè)例子里，起始狀態(tài)和結(jié)束狀態(tài)剛好是同一個(gè)狀態(tài)。標(biāo)有字符”a”的箭頭從AB指向aB，代表如果分析器處于狀態(tài)AB并且讀入的字符是a的話，就轉(zhuǎn)移到狀態(tài)aB上。

 

我們把這個(gè)狀態(tài)圖應(yīng)用在兩個(gè)字符串上，分別是”abaabbba”和”aababbaba”。其中，第一個(gè)字符串是可以接受的，第二個(gè)字符串是不可接受的(因?yàn)橛?/span>5個(gè)a和4個(gè)b)。

 

分析第一個(gè)字符串的時(shí)候，狀態(tài)機(jī)所經(jīng)過的狀態(tài)是：

AB[a]aB[b]ab[a]Ab[a]ab[b]aB[b]ab[b]aB[a]AB

分析第二個(gè)字符串的時(shí)候，狀態(tài)機(jī)所經(jīng)過的狀態(tài)是：

AB[a]aB[a]AB[b]Ab[a]ab[b]aB[b]ab[a]Ab[b]AB[a]aB

 

第一個(gè)字符串”abaabbba”讓狀態(tài)機(jī)在狀態(tài)AB上停了下來，于是這個(gè)字符串是可以接受的。第二個(gè)字符串”aababbaba”讓狀態(tài)機(jī)在狀態(tài)aB上停了下來，于是這個(gè)字符串是不可以接受的。

 

在機(jī)器內(nèi)部表示這個(gè)狀態(tài)圖的話，我們可以使用一種比較簡單的方法。這種方法僅僅把狀態(tài)與狀態(tài)之間的箭頭、起始狀態(tài)和結(jié)束狀態(tài)集合記錄下來。對應(yīng)于這個(gè)狀態(tài)圖的話，我們就可以把這個(gè)狀態(tài)圖表示成以下形式：

 

起始狀態(tài)：AB

結(jié)束狀態(tài)集合：AB

(AB,a,aB)

(AB,b,Ab)

(aB,a,AB)

(aB,b,ab)

(Ab,a,ab)

(Ab,b,AB)

(ab,a,Ab)

(ab,b,aB)

 

用一個(gè)狀態(tài)圖來表示狀態(tài)機(jī)的時(shí)候有時(shí)候會遇到確定性與非確定性的問題。所謂的確定性就是指對于任何一個(gè)狀態(tài)，輸入一個(gè)字符都可以跳轉(zhuǎn)到另一個(gè)確定的狀態(tài)中去。確定性和非確定性的區(qū)別有一個(gè)直觀的描述：狀態(tài)圖的任何一個(gè)狀態(tài)都可以有不定數(shù)量的邊指向另一個(gè)狀態(tài)，如果在這些邊里面，存在兩條邊，它們所承載的字符如果相同，那么這個(gè)狀態(tài)輸入這個(gè)就字符可以跳轉(zhuǎn)到另外兩個(gè)狀態(tài)中去，于是該狀態(tài)機(jī)就是不確定的。如圖所示：

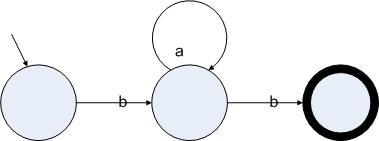
圖3.2

正則表達(dá)式ba*b的一個(gè)確定的狀態(tài)機(jī)表示

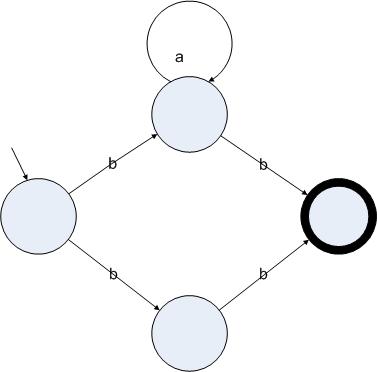
圖3.3

正則表達(dá)式ba*b的一個(gè)非確定的狀態(tài)機(jī)表示

 

圖3.3中的狀態(tài)機(jī)的起始狀態(tài)讀入字符b后可以跳轉(zhuǎn)到中間的兩個(gè)狀態(tài)里，因此這個(gè)狀態(tài)機(jī)是非確定的。相反，圖3.2中的狀態(tài)機(jī)，雖然功能跟圖3.3的狀態(tài)機(jī)一致，但卻是確定的。我們還可以使用一種特殊的邊來進(jìn)行狀態(tài)的轉(zhuǎn)換。我們用ε邊來表示一個(gè)狀態(tài)可以不讀入字符就跳轉(zhuǎn)到另一個(gè)狀態(tài)上。下圖給出了一個(gè)跟圖3.3功能一致的包含ε邊的非確定的狀態(tài)機(jī)：

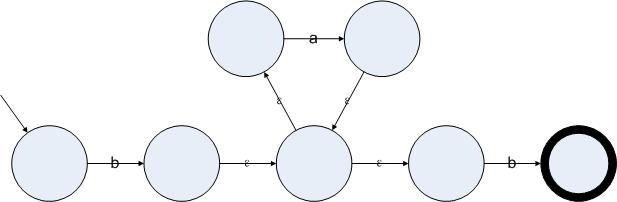
圖3.4

正則表達(dá)式ba*b的一個(gè)帶有ε邊的非確定的狀態(tài)機(jī)

 

在教科書中，通常把確定的有窮狀態(tài)自動機(jī)(有窮狀態(tài)自動機(jī)也就是本文討論的這種狀態(tài)機(jī))稱為DFA，把非確定的有窮狀態(tài)自動機(jī)稱為NFA，把帶有ε邊的非確定的狀態(tài)機(jī)稱為ε-NFA。下文中也將采用這幾個(gè)術(shù)語來指示各種類型的有窮狀態(tài)自動機(jī)。

 

在剛剛接觸到ε邊的時(shí)候，一個(gè)通常的疑問就是這種邊存在的理由。事實(shí)上如果是人直接畫狀態(tài)機(jī)的話，有時(shí)候也可以直接畫出一個(gè)確定的狀態(tài)機(jī)，復(fù)雜一點(diǎn)的話也可以畫出一個(gè)非確定的狀態(tài)機(jī)，在有些極端的情況下我們需要使用ε邊來更加簡潔的表示我們的意圖。不過ε邊存在的最大的理由就是：我們可以通過使用ε邊來給出一個(gè)簡潔的算法把一個(gè)正則表達(dá)式轉(zhuǎn)換成ε-NFA。

 

四、從正則表達(dá)式到ε-NFA

 

通過第二節(jié)所描述的內(nèi)容，我們知道一個(gè)正則表達(dá)式的基本元素就是字符集。通過對規(guī)則的串聯(lián)、并聯(lián)、重復(fù)、可選等操作，我們可以構(gòu)造除更復(fù)雜的正則表達(dá)式。如果從正則表達(dá)式構(gòu)造狀態(tài)機(jī)的時(shí)候也可以用這幾種操作對狀態(tài)圖進(jìn)行組合的話，那么方法將會變得很簡單。接下來我們將一一對這5個(gè)構(gòu)造正則表達(dá)式的方法進(jìn)行討論。使用下文描述的算法構(gòu)造出來的所有ε-NFA都有且只有一個(gè)結(jié)束狀態(tài)。

 

1：字符集

 

字符集是正則表達(dá)式最基本的元素，因此反映到狀態(tài)圖上，字符集也會是構(gòu)成狀態(tài)圖的基本元素。對于字符集C，如果有一個(gè)規(guī)則只接受C的話，這個(gè)規(guī)則對應(yīng)的狀態(tài)圖將會被構(gòu)造成以下形式：

 

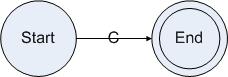
圖4.1

 

這個(gè)狀態(tài)圖的初始狀態(tài)是Start，結(jié)束狀態(tài)是End。Start狀態(tài)讀入字符集C跳轉(zhuǎn)到End狀態(tài)，不接受其他字符集。

 

2：串聯(lián)

 

如果我們使用A⊙B表示規(guī)則A和規(guī)則B的串聯(lián)，我們可以很容易的知道串聯(lián)這個(gè)操作具有結(jié)合性，也就是說(A⊙B)⊙C=A⊙(B⊙C)。因此對于n個(gè)規(guī)則的串聯(lián)，我們只需要先將前n-1個(gè)規(guī)則進(jìn)行串連，然后把得到的規(guī)則看成一個(gè)整體，跟最后一個(gè)規(guī)則進(jìn)行串聯(lián)，那么就得到了所有規(guī)則的串聯(lián)。如果我們知道如何將兩個(gè)規(guī)則串聯(lián)起來的話，也就等于知道了如何把n個(gè)規(guī)則進(jìn)行串聯(lián)。

 

為了將兩個(gè)串聯(lián)的規(guī)則轉(zhuǎn)換成一個(gè)狀態(tài)圖，我們只需要先將這兩個(gè)規(guī)則轉(zhuǎn)換成狀態(tài)圖，然后讓第一個(gè)狀態(tài)的結(jié)束狀態(tài)跳轉(zhuǎn)到第二個(gè)狀態(tài)圖的起始狀態(tài)。這種跳轉(zhuǎn)必須是不讀入字符的跳轉(zhuǎn)，也就是令這兩個(gè)狀態(tài)等價(jià)。因此，第一個(gè)狀態(tài)圖跳轉(zhuǎn)到了結(jié)束狀態(tài)的時(shí)候，就可以當(dāng)成第二個(gè)狀態(tài)圖的起始狀態(tài)，繼續(xù)第二個(gè)規(guī)則的檢查。因此我們使用了ε邊連接兩個(gè)狀態(tài)圖：

圖4.2

 

3：并聯(lián)

 

并聯(lián)的方法跟串聯(lián)類似。為了可以在起始狀態(tài)讀入一個(gè)字符的時(shí)候就知道這個(gè)字符可能走的是并聯(lián)的哪一些分支并進(jìn)行跳轉(zhuǎn)，我們需要先把所有分支的狀態(tài)圖構(gòu)造出來，然后把起始狀態(tài)連接到所有分支的起始狀態(tài)上。而且，在某個(gè)分支成功接受了一段字符串之后，為了讓那個(gè)狀態(tài)圖的結(jié)束狀態(tài)反映在整個(gè)狀態(tài)圖的結(jié)束狀態(tài)上，我們也把所有分支的結(jié)束狀態(tài)都連接到大規(guī)則的結(jié)束狀態(tài)上。如下所示：

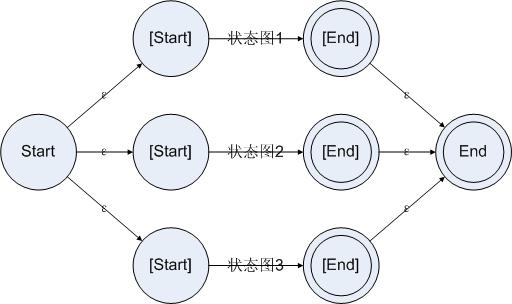
圖4.3

 

4：重復(fù)

 

對于一個(gè)重復(fù)，我們可以設(shè)立兩個(gè)狀態(tài)。第一個(gè)狀態(tài)是起始狀態(tài)，第二個(gè)狀態(tài)是結(jié)束狀態(tài)。當(dāng)狀態(tài)走到結(jié)束狀態(tài)的時(shí)候，如果遇到一個(gè)可以讓規(guī)則接受的字符串，則再次回到結(jié)束狀態(tài)。這樣的話就可以用一個(gè)狀態(tài)圖來表示重復(fù)了。于是對于重復(fù)，我們可以構(gòu)造狀態(tài)圖如下所示：

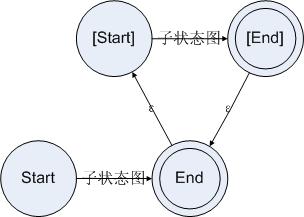
圖4.4

 

5：可選

 

為可選操作建立狀態(tài)圖比較簡單。為了完成可選操作，我們需要在接受一個(gè)字符的時(shí)候，如果字符串的前綴被當(dāng)前規(guī)則接受則走當(dāng)前規(guī)則的狀態(tài)圖，如果可選規(guī)則的后續(xù)規(guī)則接受了字符串則走后續(xù)規(guī)則的狀態(tài)圖，如果都接受的話就兩個(gè)圖都要走。為了達(dá)到這個(gè)目的，我們把規(guī)則的狀態(tài)圖的起始狀態(tài)和結(jié)束狀態(tài)連接起來，得到了如下狀態(tài)圖：

 

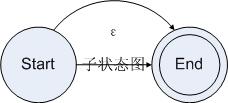
圖4.5

 

如果重復(fù)使用的是0次以上重復(fù)，也就是原來的重復(fù)加上可選的結(jié)果，那么可以簡單地把圖4.4的Start狀態(tài)去掉，讓End狀態(tài)同時(shí)擁有起始狀態(tài)和結(jié)束狀態(tài)兩個(gè)角色，[Start]和[End]則保持原狀。

 

至此，我們已經(jīng)將5種構(gòu)造狀態(tài)圖的辦法都對應(yīng)到了5種構(gòu)造規(guī)則的辦法上了。對于任意的一個(gè)正則表達(dá)式，我們僅需要把這個(gè)表達(dá)式還原成那5種構(gòu)造的嵌套，然后把每一步構(gòu)造都對應(yīng)到一個(gè)狀態(tài)圖的構(gòu)造上，就可以將一個(gè)正則表達(dá)式轉(zhuǎn)換成一個(gè)ε-NFA了。舉個(gè)例子，我們使用正則表達(dá)式來表達(dá)“一個(gè)字符串僅包含偶數(shù)個(gè)a和偶數(shù)個(gè)b”，然后把它轉(zhuǎn)換成ε-NFA。

 

我們先對這個(gè)問題進(jìn)行分析。如果一個(gè)字符串僅包含偶數(shù)個(gè)a和偶數(shù)個(gè)b的話，那么這個(gè)字符串一定是偶數(shù)長度的。于是我們可以把這個(gè)字符串分割成兩個(gè)兩個(gè)的字符段。而且這些字符段只有四種：aa、bb、ab和ba。對于aa和bb來說，無論出現(xiàn)多少次都不會影響字符串中a和b的數(shù)量的奇偶性(理由：在一個(gè)模2加法系統(tǒng)里，0是不變項(xiàng)，也就是說對于任何屬于模2加法的數(shù)X有X+0 = 0+X = X)。對于ab和ba的話，如果一個(gè)字符串的開始和結(jié)束是ab或者ba，中間的部分是aa或者bb的任意組合，這個(gè)字符串也是具有偶數(shù)個(gè)a和偶數(shù)個(gè)b的。我們現(xiàn)在得到了兩種構(gòu)造偶數(shù)個(gè)a和偶數(shù)個(gè)b的字符串的方法。把串聯(lián)、并聯(lián)、可選、重復(fù)等操作應(yīng)用在這些字符串上，仍然會得到具有偶數(shù)個(gè)a和偶數(shù)個(gè)b的字符串。于是我們可以把正則表達(dá)式書寫成以下形式：

((aa|bb)|((ab|ba)(aa|bb)*(ab|ba)))*

根據(jù)上文提到的方法，我們可以把這個(gè)正則表達(dá)式轉(zhuǎn)換成以下狀態(tài)機(jī)：

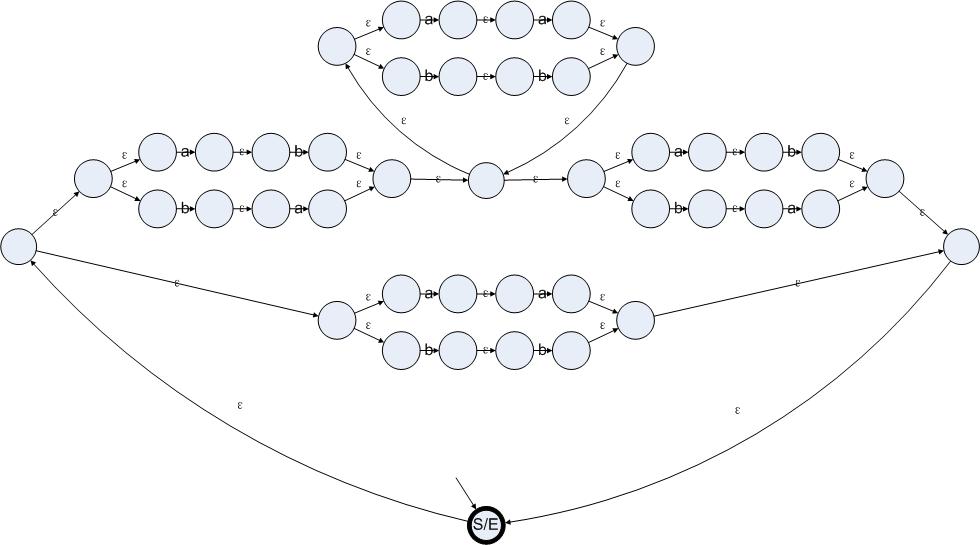 圖4.6 

至此，我們已經(jīng)得到了把一個(gè)正則表達(dá)式轉(zhuǎn)換為ε-NFA的方法了。但是只得到ε-NFA還是不行的，因?yàn)?#949;-NFA的不確定性太大了，直接根據(jù)ε-NFA跑的話，每一次都會得到大量的臨時(shí)狀態(tài)集合，會極大地降低效率。因此，我們還需要一個(gè)辦法消除一個(gè)狀態(tài)機(jī)的非確定性。

 

五、消除非確定性

 

消除ε邊算法

 

我們見到的有窮狀態(tài)自動機(jī)一共有三種：ε-NFA、NFA和DFA。現(xiàn)在我們需要將ε-NFA轉(zhuǎn)換為DFA。一個(gè)DFA中不可能出現(xiàn)ε邊，所以我們首先要消除ε邊。消除ε邊算法基于一個(gè)很簡單的想法：如果狀態(tài)A通過ε邊到達(dá)狀態(tài)B的話，那么狀態(tài)A無需讀入字符就可以直達(dá)狀態(tài)B。如果狀態(tài)B需要讀入字符x才可以到達(dá)狀態(tài)C的話，那么狀態(tài)A讀入x也可以到達(dá)狀態(tài)C。因?yàn)閺?/span>A到C的路徑是A B C，其中A到B不需要讀入字符。

 

于是我們會得到一個(gè)很自然的想法：消除從狀態(tài)A出發(fā)的ε邊，只需要尋找所有從A開始僅通過ε邊就可以到達(dá)的狀態(tài)，并把從這些狀態(tài)觸出發(fā)的非ε邊復(fù)制到A上即可。剩下的工作就是刪除所有的ε邊和一些因?yàn)橄?#949;邊而變得不可到達(dá)的狀態(tài)。為了更加形象地描述消除ε邊算法，我們從正則表達(dá)式(ab|cd)*構(gòu)造一個(gè)ε-NFA，并在此狀態(tài)機(jī)上應(yīng)用消除ε邊算法。

 

正則表達(dá)式(ab|cd)*的狀態(tài)圖如下所示：

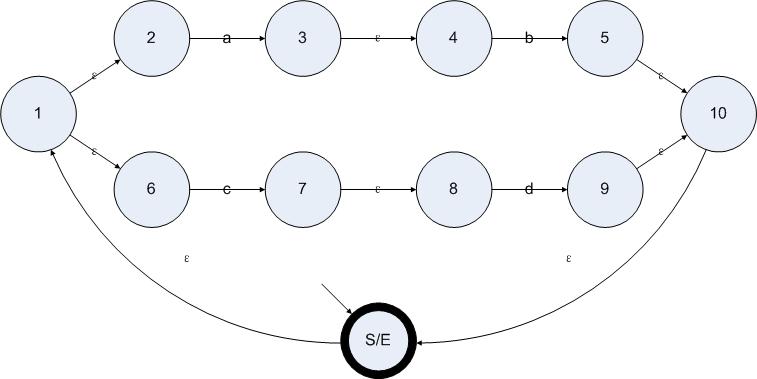
圖5.1

1：找到所有有效狀態(tài)。

 

有效狀態(tài)就是在完成了消除ε邊算法之后仍然存在的狀態(tài)。我們可以在開始整個(gè)算法之前就預(yù)先計(jì)算出所有有效狀態(tài)。有效狀態(tài)的特點(diǎn)是存在非ε邊的輸入。同時(shí)，起始狀態(tài)也是一個(gè)有效狀態(tài)。結(jié)束狀態(tài)不一定是有效狀態(tài)，但是如果存在一個(gè)有效狀態(tài)可以僅通過ε邊到達(dá)結(jié)束狀態(tài)的話，那么這個(gè)狀態(tài)應(yīng)該被標(biāo)記為結(jié)束狀態(tài)。因此對一個(gè)ε-NFA應(yīng)用消除ε邊算法產(chǎn)生的NFA可能出現(xiàn)多個(gè)結(jié)束狀態(tài)。不過起始狀態(tài)仍然只有一個(gè)。

 

我們可以把“存在非ε邊的輸入或者起始狀態(tài)”這個(gè)判斷方法應(yīng)用在圖5.1每一個(gè)狀態(tài)上，計(jì)算出圖5.1中所有的有效狀態(tài)。結(jié)果如下圖所示。

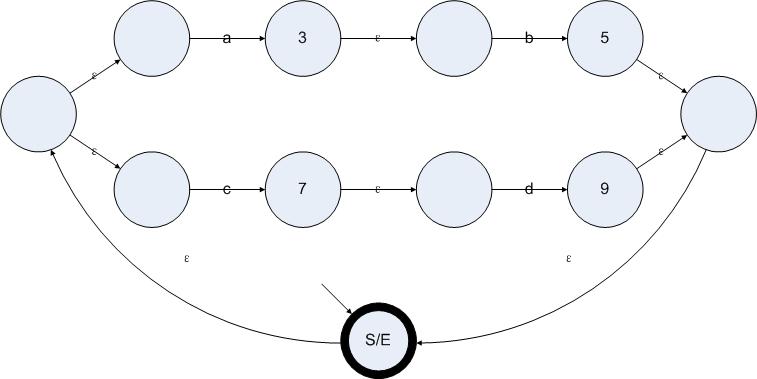
圖5.2

所有非有效狀態(tài)的標(biāo)簽都被刪除

 

如果一個(gè)狀態(tài)同時(shí)具有ε邊和非ε邊輸入的話，那么這個(gè)狀態(tài)仍然是有效狀態(tài)。因?yàn)樗械挠行顟B(tài)在下一步的操作中，都會得到新的輸出和新的輸入。

 

2：添加所有必要的邊

 

接下來我們要對所有的有效狀態(tài)都應(yīng)用一個(gè)算法。這個(gè)算法分成兩步。第一步是尋找一個(gè)狀態(tài)的ε閉包，第二步是把這個(gè)狀態(tài)的ε閉包看成一個(gè)整體，把所有從這個(gè)閉包中輸出的邊全部復(fù)制到當(dāng)前狀態(tài)上。從標(biāo)記有效狀態(tài)的結(jié)果我們得到了圖5.1狀態(tài)圖的有效狀態(tài)集合是{S/E 3 5 7 9}。我們依次對這些狀態(tài)應(yīng)用上述算法。第一步，計(jì)算S/E狀態(tài)的ε閉包。所謂一個(gè)狀態(tài)的ε閉包就是從這個(gè)狀態(tài)出發(fā)，僅通過ε邊就可以到達(dá)的所有狀態(tài)的集合。下圖中標(biāo)記出了狀態(tài)S/E的ε閉包：

 

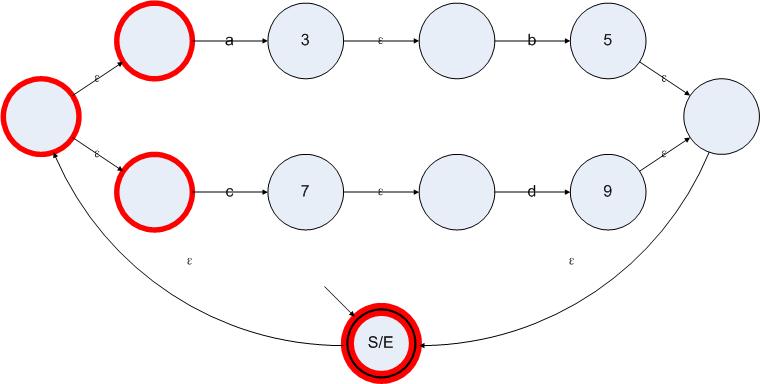
圖5.3

現(xiàn)在，我們把狀態(tài)S/E從狀態(tài)S/E的ε閉包中排除出去。因?yàn)閺臓顟B(tài)A輸出的非ε邊都屬于從狀態(tài)A的ε閉包中輸出的非ε邊，復(fù)制這些邊是沒有任何價(jià)值的。接下來就是找到從狀態(tài)S/E的ε閉包中輸出的非ε邊。在圖5.3我們可以很容易地發(fā)現(xiàn)，從狀態(tài)1和狀態(tài)6(見圖5.1的狀態(tài)標(biāo)簽)分別輸出到狀態(tài)3和狀態(tài)7的標(biāo)記了a或者b的邊，就是我們所要尋找的邊。接下來我們把這些邊復(fù)制到狀態(tài)S/E上，邊的目標(biāo)狀態(tài)仍然保持不變，可以得到下圖：

 

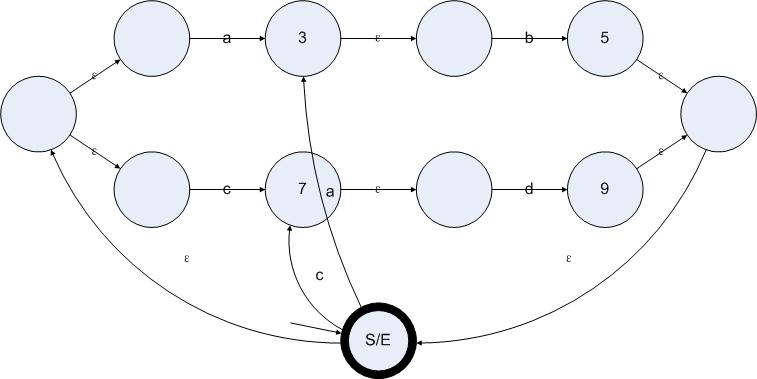
圖5.4

至此，這個(gè)算法在S/E上的應(yīng)用就結(jié)束了，接下來我們分別對剩下的有效狀態(tài){3 5 7 9}分別應(yīng)用此算法，可以得到下圖：

 
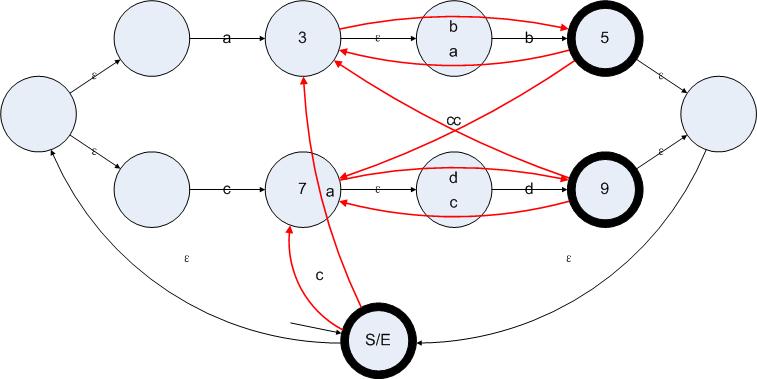
圖5.5

紅色的邊為新增加的邊

 

3：刪除所有ε邊和無效狀態(tài)

 

這一步操作是消除ε邊算法的最后步驟。我們只需要?jiǎng)h除所有的ε邊和無效狀態(tài)就完成了整個(gè)消除ε邊算法。現(xiàn)在我們對圖5.5的狀態(tài)機(jī)應(yīng)用第三步，得到如下狀態(tài)圖：

 
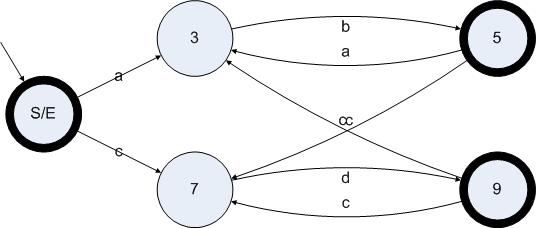
圖5.6

 

不過并不是只有新增的邊才不被刪除。根據(jù)定義，所有從有效狀態(tài)出發(fā)的非ε邊都是不能刪除的邊。

 

我們通過把消除ε邊算法應(yīng)用在圖5.1的狀態(tài)機(jī)上，得到了圖5.6這個(gè)DFA。但是并不是所有的消除ε邊算法都可以直接從ε-NFA直接得到DFA，這個(gè)其實(shí)跟正則表達(dá)式本身有關(guān)。至于什么正則表達(dá)式可以達(dá)到這個(gè)效果這里就不深究了。但是因?yàn)橛锌赡墚a(chǎn)生NFA，所以我們還需要一個(gè)算法把NFA轉(zhuǎn)換成DFA。

 

從NFA到DFA

 

NFA是非確定性的狀態(tài)機(jī)，DFA是確定性的狀態(tài)機(jī)。確定性和非確定性的最大區(qū)別就是：從一個(gè)狀態(tài)讀入一個(gè)字符，確定性的狀態(tài)機(jī)得到一個(gè)狀態(tài)，而非確定性的狀態(tài)機(jī)得到一個(gè)狀態(tài)的集合。如果我們把NFA的起始狀態(tài)S看成一個(gè)集合{S}的話，對于一個(gè)狀態(tài)集合S’，給定一個(gè)輸入，就可以用NFA計(jì)算出對應(yīng)的狀態(tài)集合T’。因此我們在構(gòu)造DFA的時(shí)候，只需要把起始狀態(tài)對應(yīng)到S’，并且找到所有可能在NFA同時(shí)出現(xiàn)的狀態(tài)集合，把這些集合都轉(zhuǎn)換成DFA的一個(gè)狀態(tài)，那么任務(wù)就完成了。因?yàn)?/span>NFA的狀態(tài)是有限的，所以NFA所有狀態(tài)的集合的冪集的元素個(gè)數(shù)也是有限的，因此使用這個(gè)方法構(gòu)造DFA是完全可能的。

 

為了形象地表達(dá)出這個(gè)算法的過程，我們將構(gòu)造一個(gè)正則表達(dá)式，然后給出該正則表達(dá)式轉(zhuǎn)換成NFA的結(jié)果，并把構(gòu)造DFA的算法應(yīng)用在NFA上。假設(shè)一個(gè)字符串只有a、b和c三種字符，判斷一個(gè)字符串是不是以abc開始并且以cba結(jié)束正則表達(dá)式如下：

abc(a|b|c)*cba

通過上文的算法，可以得出如下圖所示的NFA：

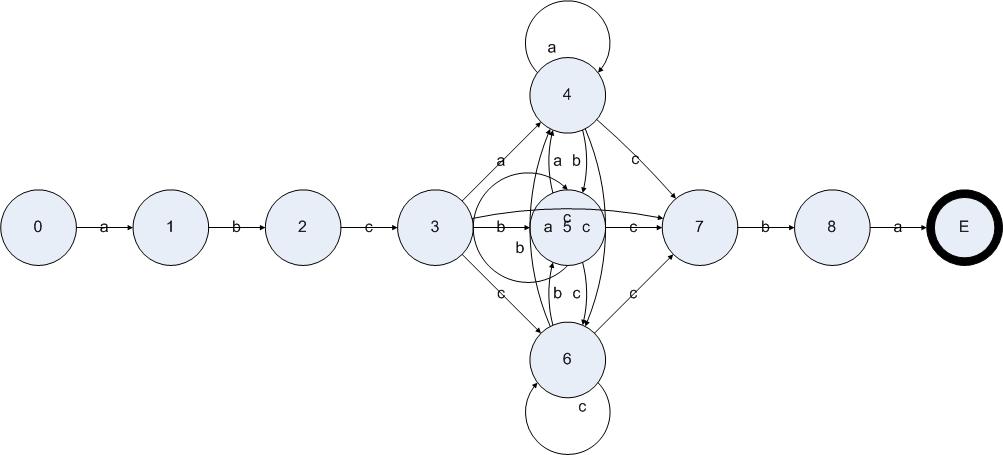
圖5.7

 

現(xiàn)在我們開始構(gòu)造DFA，具體算法如下：

 

1：把{S}放進(jìn)隊(duì)列L和集合D中。其中S是NFA的起始狀態(tài)。隊(duì)列L放置的是未被處理的已經(jīng)創(chuàng)建了的DFA狀態(tài)，集合D放置的是已經(jīng)存在的DFA狀態(tài)。根據(jù)上文的討論，DFA的每一個(gè)狀態(tài)都對應(yīng)著NFA的一些狀態(tài)。

 

2：從隊(duì)列L中取出一個(gè)狀態(tài)，計(jì)算從這個(gè)狀態(tài)輸出的所有邊所接受的字符集的并集，然后對該集合中的每一個(gè)字符尋找接受這個(gè)字符的邊，把這些邊的目標(biāo)狀態(tài)的并集T計(jì)算出來。如果T∈D則代表當(dāng)前字符指向了一個(gè)已知的DFA狀態(tài)。否則則代表當(dāng)前字符指向了一個(gè)未創(chuàng)建的DFA狀態(tài)，這個(gè)時(shí)候就把T放進(jìn)L和D中。在這個(gè)步驟里有兩層循環(huán)：第一層是遍歷所有接受的字符的并集，第二層是對每一個(gè)可以接受的字符遍歷所有輸出的邊計(jì)算目標(biāo)DFA狀態(tài)所包含的NFA狀態(tài)的集合。

 

3：如果L非空則跳到2。

 

現(xiàn)在我們開始對圖5.7的狀態(tài)機(jī)應(yīng)用DFA構(gòu)造算法。

 

首先執(zhí)行第一步，我們得到：

圖5.8

 

從上到下分別是隊(duì)列L、集合D和DFA的當(dāng)前狀態(tài)。就這樣一直執(zhí)行該算法直到狀態(tài)3進(jìn)入集合D，我們得到：

 
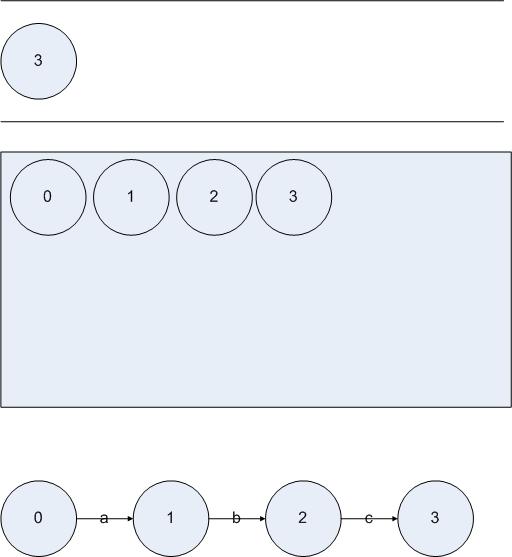
圖5.9

 

現(xiàn)在從隊(duì)列L中取出{3}，經(jīng)過分析得到狀態(tài)集合{3}接受的字符集合為{a b c}。{3}讀入a到達(dá){4}，讀入b到達(dá){5}，讀入c到達(dá){6 7}。因?yàn)?/span>{4}、{5}和{6 7}都不屬于D，所以把它們都放入隊(duì)列L和集合D：

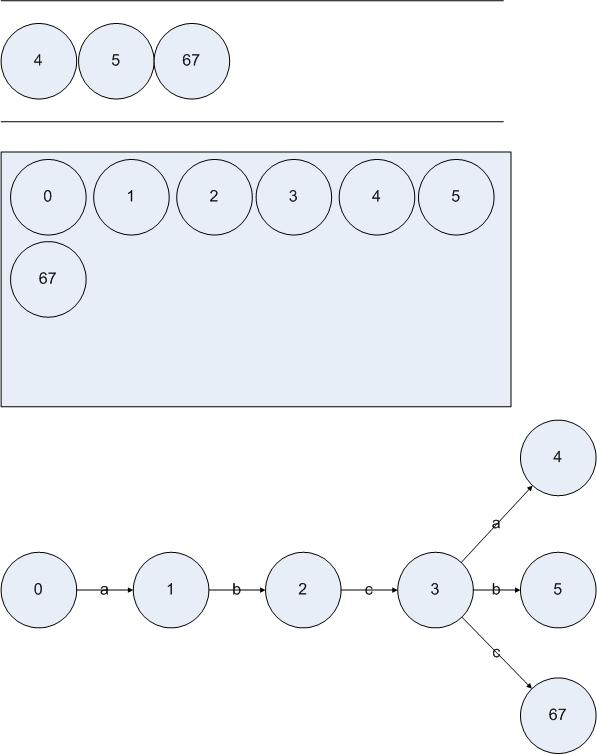
圖5.10

 

從隊(duì)列中取出4進(jìn)行計(jì)算，我們得到：

 
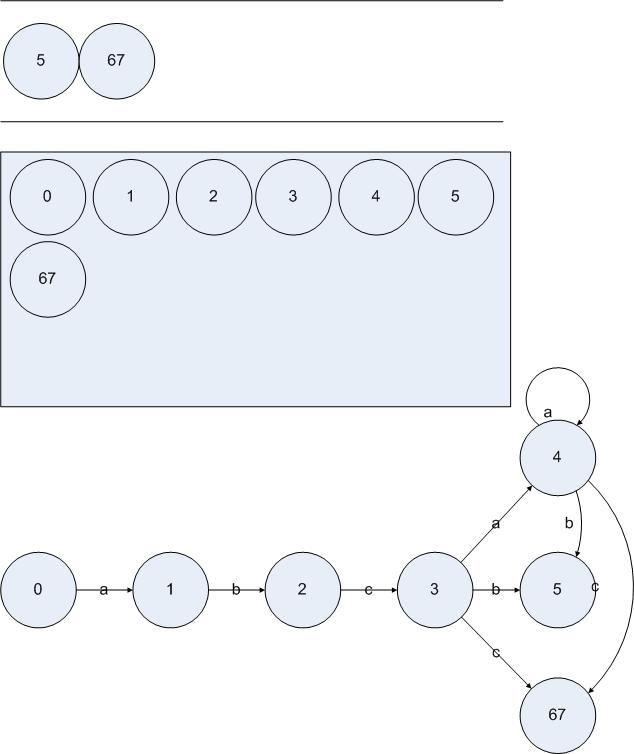
圖5.11

 

顯然，對于狀態(tài){4}的處理并沒有發(fā)現(xiàn)新的DFA狀態(tài)。于是處理{5}和{6 7}，我們可以得到：

 
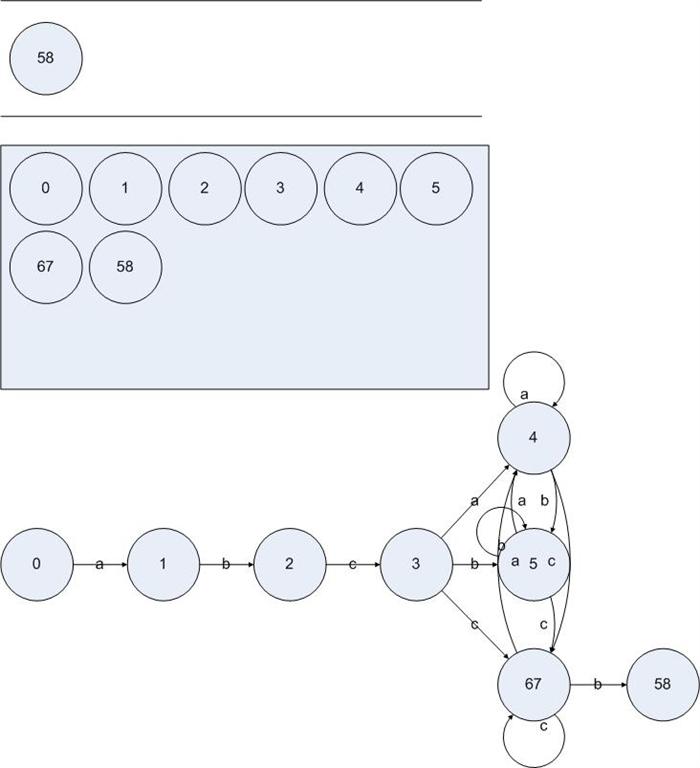
圖5.12

 

在處理狀態(tài){5}的時(shí)候沒有發(fā)現(xiàn)新的DFA狀態(tài)，處理{6 7}在輸入{a c}之后的跳轉(zhuǎn)也沒有發(fā)現(xiàn)新的DFA狀態(tài)，但是我們發(fā)現(xiàn)了{6 7}輸入b卻得到了新的DFA狀態(tài){5 8}。把算法執(zhí)行完，我們得到一個(gè)DFA：
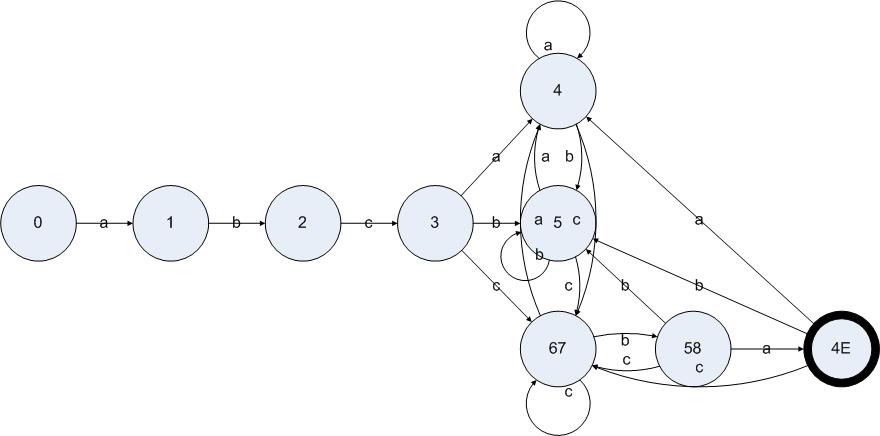圖5.13

 

至此，對圖5.7的狀態(tài)機(jī)應(yīng)用DFA構(gòu)造算法的流程就結(jié)束了，我們得到了圖5.13的DFA，其功能與圖5.7的NFA等價(jià)。在DFA中，起始狀態(tài)是0，結(jié)束狀態(tài)是4E。凡是包含了NFA的結(jié)束狀態(tài)的DFA狀態(tài)都必須是結(jié)束狀態(tài)。

 

六、使用正則表達(dá)式構(gòu)造詞法分析器

 

判斷一個(gè)字符串是否屬于某規(guī)則的算法介紹到這里就結(jié)束了。回到我們一開始的問題上，我們需要使用一些規(guī)則來吧一個(gè)長的字符串?dāng)嚅_成記號，然后計(jì)算出每一個(gè)記號對應(yīng)的規(guī)則。在解決這個(gè)問題之前，我們先考察一下能夠成功地被詞法分析器接受的字符串應(yīng)該是什么樣子的。

 

假設(shè)我們現(xiàn)在有規(guī)則A、B、C和D，分別對應(yīng)于四種記號類型，那么被詞法分析器接受的字符串就是A、B、C和D的任意組合，也就是(A|B|C|D)*。如果規(guī)定了輸入的字符串不能為空的話，那么被詞法分析器接受的字符串就是(A|B|C|D)+。但是單純地使用(A|B|C|D)+作為一個(gè)規(guī)則去應(yīng)用在輸入的字符串的話，我們只能夠判斷字符串是否是詞法分析器能夠接受的字符串。因此我們需要對這個(gè)方法進(jìn)行修改。

 

首先按照上文的方法，把每一個(gè)記號類型對應(yīng)的規(guī)則的正則表達(dá)式轉(zhuǎn)換成DFA，然后使用并聯(lián)的方法將他們組合起來，但是并不使用“重復(fù)”。但是這次我們要做一點(diǎn)修改，我們要把新的DFA的每一個(gè)狀態(tài)對應(yīng)的規(guī)則的DFA狀態(tài)集合記住。

 

這里給出一個(gè)例子，我們假設(shè)需要一個(gè)簡單語言的詞法分析器，規(guī)則如下：

 

I：[a-zA-Z_][a-zA-Z_0-9]*

N：[0-9]+

R：[0-9]+.[0-9]+

O：[=>+-*/|&]

 

按照規(guī)則構(gòu)造出四個(gè)DFA并將它們組合起來：

 
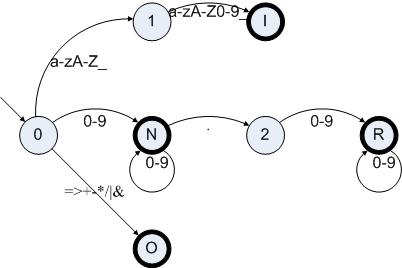
圖6.1

我們構(gòu)造出了I|N|R|O的DFA，并且標(biāo)識出了哪些狀態(tài)包含了原DFA的結(jié)束狀態(tài)。這樣做的一個(gè)好處是，當(dāng)我們把一個(gè)字符串放進(jìn)這樣的一個(gè)DFA之后，我們就一直等待整個(gè)字符串被接受，或者失敗。如果字符串被接受的話，我們就把當(dāng)前的結(jié)束狀態(tài)記下來。如果失敗的話，我們就把這個(gè)狀態(tài)機(jī)在分析字符串的時(shí)候經(jīng)過的最后一個(gè)結(jié)束狀態(tài)記下來。這個(gè)時(shí)候，結(jié)束狀態(tài)所代表的原DFA結(jié)束狀態(tài)的相應(yīng)記號類型就是我們所需要的信息了。如果得不到任何結(jié)束狀態(tài)的話，輸入的字符串就是不背詞法分析其接受的。

 

舉個(gè)例子，使用上述狀態(tài)機(jī)分析”123.ABC”。

 

首先從狀態(tài)0開始，依次經(jīng)過狀態(tài)N N N 2，然后宣告失敗。最后一個(gè)N(結(jié)束狀態(tài))以及當(dāng)時(shí)被接受的字符串”123”被識別，結(jié)果為(N，”123”)。然后從”.ABC”開始，輸入第一個(gè)記號就失敗了，于是”.”被識別為不可接受字串。最后輸入”ABC”，依次經(jīng)過狀態(tài)0 1 I I，然后字符串結(jié)束并且被接受，于是輸出(I，”ABC”)。

 

為什么我們在構(gòu)造狀態(tài)機(jī)的時(shí)候不使用“重復(fù)”呢？因?yàn)樵诿恳粋€(gè)記號被識別出的時(shí)候，我們都要做一些額外的工作。如果我們使用“重復(fù)”來構(gòu)造詞法分析器的狀態(tài)機(jī)，我們將無從知道一個(gè)記號被識別出來的確切時(shí)間。

 

算法到這里基本上就結(jié)束了，不過還存在一些小問題需要在細(xì)節(jié)上解決。一般來說我們給出的一些構(gòu)成詞法分析器的規(guī)則很少有沖突，不過偶爾會出現(xiàn)兩個(gè)規(guī)則所代表的字符串集合存在交集的情況。有了DFA這個(gè)工具，我們可以很輕易地識別出規(guī)則沖突。

 

假如我們的詞法分析器有A和B兩個(gè)狀態(tài)，那么我們構(gòu)造詞法分析器A|B的時(shí)候，將會得到一些包含DFA(A)和DFA(B)的結(jié)束狀態(tài)的新狀態(tài)。我們只需要檢查這些狀態(tài)是否具有以下特征，就可以判斷A和B的關(guān)系。我們假設(shè)DFA(A)為規(guī)則A的狀態(tài)機(jī)，DFA(B)為規(guī)則B的狀態(tài)機(jī)，DFA(L)為詞法分析器A|B的狀態(tài)機(jī)：

 

1：如果DFA(L)存在一個(gè)或多個(gè)狀態(tài)同時(shí)包含了DFA(A)和DFA(B)的結(jié)束狀態(tài)，那么A和B所代表的字符串存在交集。

2：如果DFA(L)不存在同時(shí)包含了DFA(A)和DFA(B)的結(jié)束狀態(tài)的狀態(tài)，那么A和B所代表的字符串不存在交集。

3：如果DFA(L)的某些狀態(tài)包含了DFA(A)的結(jié)束狀態(tài)，并且這些狀態(tài)都無一例外地包含了DFA(B)的結(jié)束狀態(tài)的話，那么A是B的子集。

4：如果DFA(L)的某些狀態(tài)包含了DFA(A)的結(jié)束狀態(tài)，但是這些狀態(tài)并沒有無一例外地包含DFA(B)的結(jié)束狀態(tài)的話，那么A不是B的子集。

 

在圖6.1的詞法分析器中，我們可以很清楚地看出I、N、R和O四個(gè)規(guī)則兩兩之間都不存在交集。我們可以嘗試構(gòu)造一個(gè)沖突的規(guī)則，并看一看詞法分析器的DFA是什么樣子的：

 

假設(shè)詞法分析器包含以下規(guī)則：

A：”if”

B：[a-z]+

 

對A|B構(gòu)造DFA，我們將會得到如下狀態(tài)機(jī)：

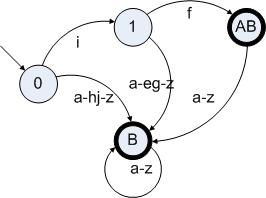
圖6.2

 

通過圖6.2我們可以看出，這個(gè)狀態(tài)圖滿足了上述的條件3：包含了狀態(tài)A的結(jié)束狀態(tài)的狀態(tài)都包含了B的結(jié)束狀態(tài)，因此A是B的子集。顯然”if”是[a-z]+的一個(gè)子集。在處理這種有沖突的規(guī)則的時(shí)候，既可以報(bào)錯(cuò)，也可以根據(jù)指定的優(yōu)先級進(jìn)行挑選。

 

七、尾聲

 

使用DFA的方法完成的可配置詞法分析器的性能是相當(dāng)好的。筆者前不久曾經(jīng)做過實(shí)驗(yàn)，首先使用本文提到的算法開發(fā)一個(gè)這樣的詞法分析器，然后在一份C++代碼(這份代碼經(jīng)過多次復(fù)制而成件，一共有3.12M)中抽取所有數(shù)字、標(biāo)識符和注釋，吞吐速度高達(dá)46萬記號/秒（筆者的臺式電腦配置是奔騰4的超線程2.99GHz處理器，1G內(nèi)存），其中抽取出來的記號一共有22萬個(gè)。在分析的過程中，只有10%的時(shí)間花在了DFA上，90%的時(shí)間花在了處理結(jié)果的工作上。DFA本身造成的消耗是很小的。不過詞法分析的性能在很大程度上跟DFA的實(shí)現(xiàn)有很大關(guān)系。三個(gè)月前筆者也實(shí)現(xiàn)過一個(gè)同類的程序，但是吞吐速度僅有1.1萬記號/秒。

 

一般來說，比較高性能的DFA的實(shí)現(xiàn)是一張二維的表。行代表字符，列代表DFA的狀態(tài)，單元格代表該狀態(tài)經(jīng)輸入某個(gè)字符之后進(jìn)行轉(zhuǎn)移的目標(biāo)狀態(tài)。此外還有一張表用來記錄哪些狀態(tài)對應(yīng)哪些規(guī)則的結(jié)束狀態(tài)。筆者的詞法分析器是基于UTF-16編碼的字符串，一張表一共有65535行顯然是不現(xiàn)實(shí)的，因此還有另一張表把字符轉(zhuǎn)換成字符類。字符類是這樣定義的：假設(shè)現(xiàn)在已經(jīng)存在了65535行的一張大表，如果在某個(gè)字符區(qū)間所對應(yīng)的子表內(nèi)，任意一列的單元格的數(shù)據(jù)都一樣的話，那么這個(gè)區(qū)間內(nèi)的所有字符就可以被視為是等價(jià)的，這些字符就屬于同一個(gè)字符類。于是僅需要另外一張65535個(gè)單元的表用來把一個(gè)字符映射到字符類。這種做法可以大大的壓縮DFA所需要的空間。在筆者的程序里，識別字符類的算法被融入了DFA的構(gòu)造算法中

 

參考文獻(xiàn)

 

【1】：Alfred V.Aho  Ravi Sethi  Jeffrey D.Ullman ，Compilers Principles , Techniques , and Tools

【2】：Dick Grune  Ceriel Jacobs ，Parsing Techniques ---- A Practical Guide

【3】：Kenneth C.Louden ，Compiler Construction Principles and Practice