《Near Optimal Hierarchical Path-Finding》中提出了一種層次A*算法,正好能夠用于解決項目大地圖尋路的問題。大致思路是:1)預處理。將地圖劃分為nxn大小的區塊,找出每個區塊與周圍四個區塊在邊界上的互通點,在區塊中使用局部A*對找出的點做連通性測試并將其保存下來;2)尋路時,使用預處理得到的數據(邊界上的可通點與區塊內部的互通點),先在區塊層級上做一次A*,根據結果再在每個區塊中使用局部A*找到區塊與區塊之間的路徑,最終得到完整路徑。
一、A* Path-Finding
A*算法就不多講了,可參考:
A*算法的優化可從搜索節點儲存和OpenList排序兩方面入手。
二、預處理
每個相鄰區塊(C1和C2)都有一條由公共邊,該邊兩側小格組成L1和L2,則連通點集E滿足下列條件:
- E ? L1 ∪ L2
- ?t ∈ L1 ∪ L2 : t ∈ E ? symm(t) ∈ E ,其中symm(t)為對稱關系
- E不含不可行走格子
對在E中且同邊的連續格子取其中點,如下圖所示:
_thumb.png)
對上面得到的位于同一區塊的點集合使用local A*做連通性測試,下圖用直線連接來表示兩點互通:
_thumb.png)
三、尋路
使用區塊連通信息,進行區塊級A*,得到區塊之間的連接點,如果在預處理時保存了區塊內互通點的路徑,就不必再進行區塊內的local A*了。
實驗結果表明,在未采用區塊內預存路徑的情況下,中長距離尋路使用層次A*后的平均效率是普通A*的5倍以上,距離越長效率對比越明顯。
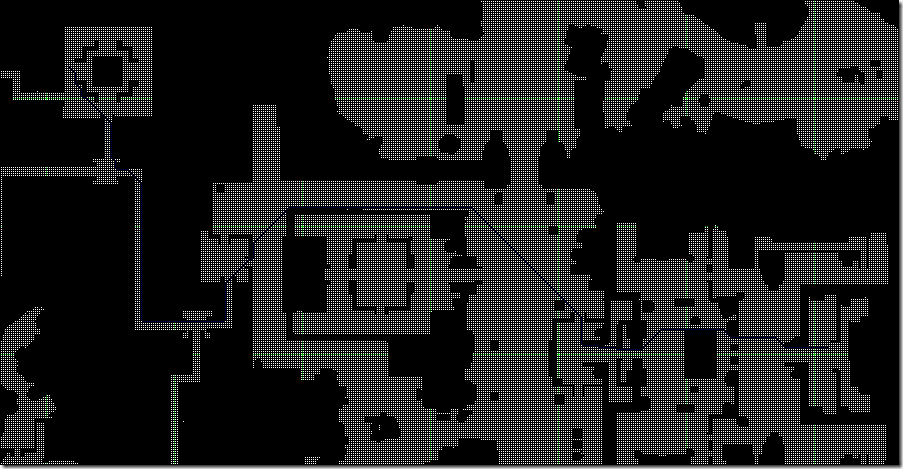
A* 93ms

HPA* 15ms
從上圖中可以看出,HPA*得到的路徑并不是最優的,它是在最優和效率上的折中,適合作為長距離尋路的一種優化方案。
四、優化點
- 可擴展為多層而不僅限于一層
- 預存區塊內連通點路徑
- 區塊邊界可通面積較大時,產生不自然路徑,如下圖所示:

一個改進的方法是對過長的邊界再做劃分:
_thumb.png)