很多DCC工具都提供了Curves Editor,通過控制點來構造插值曲線,這樣可以精確地插值軌跡。在我們游戲的過場編輯器中,我們并沒有開發這類工具,一方面由于時間人力有限,另一方面希望能夠提供一種直觀簡便的方式達到想要的效果。因此我們支持兩種攝像機路徑創建方法:1)以攝像機視角直接將攝像機擺到想要位置,保存此時攝像機的位置與旋轉;2)將3DS Max中的路徑導出為游戲的過場格式。前者可以滿足90%的過場編輯需求,后者滿足了10%的復雜路徑編輯需求。
不管使用那種方式,都需要將離散點進行插值(interpolation)以便得到平滑路徑。這里就牽涉到位置插值和朝向插值。
從插值函數上可分為三類:1)線性;2)多項式;3)樣條。顧名思義,線性插值采用線性函數,多項式插值采用多項式,而樣條插值則采用了一組多項式組成的分段函數。由于攝像機的關鍵路徑點通常都會大于2個,所以插值方法上就必須選取樣條方法。
一、位置插值
1.1 樣條類型選擇
在這里我們僅考慮三次樣條插值,因為它們可達到C2連續。三次樣條中主要以Bezier、Catmull-Rom、均勻B樣條為考查對象,它們都具有計算開銷小的優點。可以通過下面公式來定義它們:
_thumb.png)
簡化為:
_thumb.png)
下面表格列出了三種插值曲線對應的G和M:
_thumb.png)
如下圖所示,對4個點進行Bezier插值得到的曲線只會有兩個點被曲線穿過,而B-Spline插值得到的曲線不會經過控制點,只有Catmull-Rom Spline可以得到穿過除起點和終點之間的所有控制點。正因為Catmull-Rom具有這個特性,使得它被廣泛地應用在關鍵幀平滑插值上,因此我們選擇了Catmull-Rom樣條作為攝像機位置點的插值算法。
_thumb.png)
1.2 實現
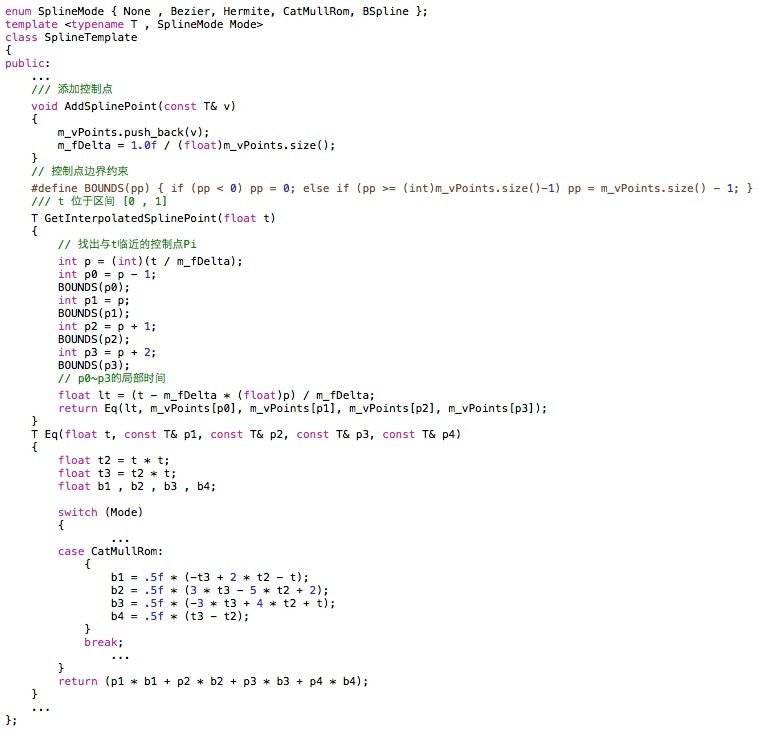
參考:
[1] Mathematics for 3D Game Programming and Computer Graphics 3e by Eric Lengyel
[2] http://en.wikipedia.org/wiki/Catmull-Rom_spline#Catmull.E2.80.93Rom_spline
[3] http://www.codeproject.com/Articles/30838/Overhauser-Catmull-Rom-Splines-for-Camera-Animatio
二、朝向(旋轉)插值
2.1 Euler Angles VS Quaternion
三維空間中描述旋轉的主要方法有Euler Angles和Quaternion。Euler Angles有三個明顯的問題:1)三軸上的旋轉順序敏感;2)Gimbal Lock現象導致旋轉自由度丟失;3)獨立地對三個旋轉分量進行插值,忽略了三軸之間的依賴關系,導致插值結果不理想。與Euler Angles不同的是,Quaternion沒有將旋轉分解到三個軸向上,而是用一個旋轉軸和繞該軸的旋轉角度來描述,所以從根本上消除了Euler Angles的三大問題。有關Quaternion的詳細描述可參考[1],在此不再累述。
2.2 LERP VS SLERP
四元數線性插值(Linear Quaternion interpolation)的計算公式為:
_thumb.jpg)
四元數球面線性插值(Spherical Linear Quaternion interpolation)的計算公式為:
_thumb.jpg)
_thumb.jpg)
其中,θ為兩個四元數的夾角。
為了方便展示,我們考慮在2D情況對角度V進行兩次插值,兩種算法在插值效果上存在的差異,如下圖(b為LERP、c為SLERP):
_thumb.jpg)
從圖中可以看出LERP其實是對兩四元數在圓上的弦進行了等分,而SLERP則是對圓弧進行等分。由此得出的結論是,SLERP得到了比LERP更平滑的插值結果。
為了保證插值曲線的C2連續性,需要使用球面四邊形插值(Spherical Quadrangle interpolation)方法。例如,對q1和q2插值,首先要用q0、q1、q2、q3計算出兩個控制點(Inner Quadrangle Point),公式如下:
_thumb.jpg)
然后通過下式得到最終插值結果:
_thumb.jpg)
2.3 實現
_thumb.jpg)
上面代碼沒有考慮兩個四元數之間夾角大于180°的情況。例如,考慮q1->q2的插值角度θ>180°,我們可以讓q1->q2反向旋轉2π-θ,即旋轉-(2π-θ),根據四元數的定義[v*sin(θ/2) , cos(θ/2)],那么對q2進行處理變為[-v*sin(θ/2) , -cos(θ/2)]。這個處理可以放在AddSplinePoint中來做:
_thumb.jpg)
參考:
[1] Quaternions, Interpolation and Animation by EB Dam - 1998
[2] Game Engine Architecture by Jason Gregory - 2009
[3] https://theory.org/software/qfa/writeup/node12.html