遞歸通常很直白地描述了一個求解過程，因此也是最容易被想到和實現(xiàn)的算法。循環(huán)其實和遞歸具有相同的特性（即：做重復任務），但有時，使用循環(huán)的算法并不會那么清晰地描述解決問題步驟。單從算法設計上看，遞歸和循環(huán)并無優(yōu)劣之別。然而，在實際開發(fā)中，因為函數(shù)調(diào)用的開銷，遞歸常常會帶來性能問題，特別是在求解規(guī)模不確定的情況下。而循環(huán)因為沒有函數(shù)調(diào)用開銷，所以效率會比遞歸高。除少數(shù)編程語言對遞歸進行了優(yōu)化外，大部分語言在實現(xiàn)遞歸算法時還是十分笨拙，由此帶來了如何將遞歸算法轉換為循環(huán)算法的問題。算法轉換應當建立在對求解過程充分理解的基礎上，有時甚至需要另辟蹊徑。
前段時間遇到過這樣的問題：已知一2D地圖格子的長寬（w、h）及每個格子的邊長（a，格子為正方形），給定物體的2D坐標（pos[x , y]）及半徑（r），求解物體在2D地圖格子中所占的格子，僅考慮n*n的情況。大概的求解過程如下：
1）根據(jù)半徑，確定n*n中的n。假定計算公式為：n = Round(2*r / a)
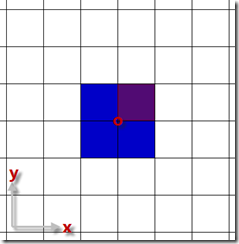
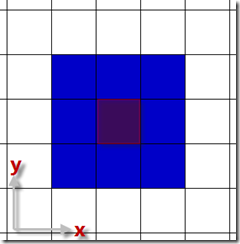
2）根據(jù)2D坐標得到物體的“中心格子”。根據(jù)n的奇偶，計算公式不同，如下圖所示。
n為偶數(shù)[1] n為奇數(shù)[2]
[1]：grid(x , y) = Round(pos / a)
[2]：grid(x , y) = Floor(pos / a)
其中，格子坐標x >= 0 , y >= 0。
3）以“中心格子”為基礎，求出物體占據(jù)的其他格子。這樣的描述，讓人容易想到遞歸，就像用深度優(yōu)先方法遍歷樹那樣，偽代碼算法如下：
if n is even
{
get the index of 'center grid' (row , col)
ExtendHeldGrid(row , col , n)
ExtendHeldGrid(row - 1 , col , n)
ExtendHeldGrid(row - 1 , col - 1 , n)
ExtendHeldGrid(row , col - 1 , n)
}
else
{
get the index of 'center grid' (row , col)
ExtendHeldGrid(row , col , n)
}
function ExtendHeldGrid(row , col , level)
{
if(level <= 0)
return
if((row >= 0 and row < MaxGridWidth) and (col >= 0 and col < MaxGridHeight))
{
mark the grid(row , col)
ExtendHeldGrid(row , col , level - 2)
if(level - 2 > 0)
{
ExtendHeldGrid(row + 1 , col , level - 2)
ExtendHeldGrid(row - 1 , col , level - 2)
ExtendHeldGrid(row , col + 1 , level - 2)
ExtendHeldGrid(row , col - 1 , level - 2)
ExtendHeldGrid(row + 1 , col + 1 , level - 2)
ExtendHeldGrid(row - 1 , col + 1 , level - 2)
ExtendHeldGrid(row + 1 , col - 1 , level - 2)
ExtendHeldGrid(row - 1 , col - 1 , level - 2)
}
}
}
雖然，該算法得到了正確的求解結果，但是由于每個格子都會標記周圍的8個格子，所以存在大量的重復，再者如果上面的過程每幀都進行的話，函數(shù)調(diào)用開銷也是相當可觀。
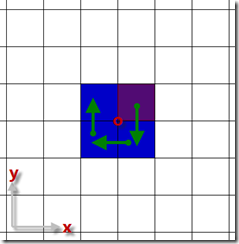
循環(huán)自然是不可避免的，消除重復便成了優(yōu)化的目標。分析格子圖和n為2和3的情況，試圖找出用循環(huán)代替遞歸的方法，我發(fā)現(xiàn)了下面一個有趣的規(guī)律：
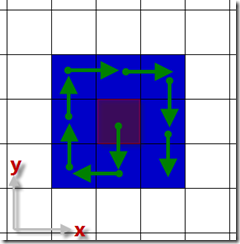
從“中心格子”出發(fā)，順時針（或逆時針）以上圖方式可以走遍所求解的每個格子而不重復。在實現(xiàn)上，每個轉角也是有規(guī)律的，可以通過一個2*2的轉角矩陣來控制：
[1 , 0][0 , -1]
[0 , 1][-1 , 0]
順時針方式的轉角陣
矩陣中的每個元素代表從當前格子走到下個格子在row和col上的變化。加之，在轉角之間的路長（以格子個數(shù)計）有每轉兩次遞增單位1的規(guī)律，算法就不難得到了，下面同樣以偽代碼示：
conerMat =
{
{0 , -1} ,
{-1 , 0} ,
{0 , 1} ,
{1 , 0}
}
dir = 0 /// 轉角控制，四個轉角順時針0~3
span = 1 /// 轉角間的跨度
count = 1 /// 每兩次增加一個跨度
rin = 1 /// 下一個轉角的循環(huán)索引
if n is even
get the index of 'center grid' (row , col)
else
get the index of 'center grid' (row , col)
for(i = 0; i < n * n; ++i)
{
if((row >= 0 and row < MaxGridWidth) and (col >= 0 and col < MaxGridHeight))
mark the grid(row , col)
if(i == rin)
{
dir = (dir + 1) % 4
if(count == 2)
{
++span
count = 1
}
else
++count
rin = i + span
}
row = row + conerMat[dir][0]
col = col + conerMat[dir][1]
}
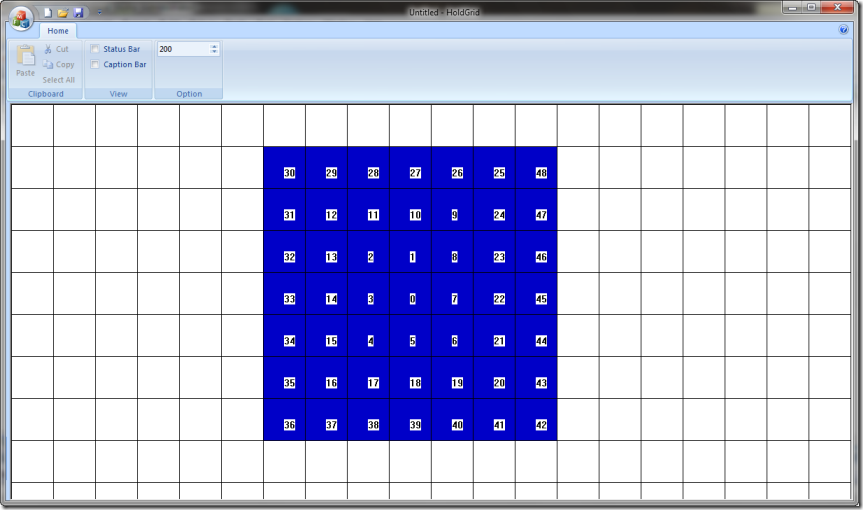
用MFC程序驗證了一下算法的正確性，標號展示了循環(huán)的路線（注意GDI的坐標系中Y的正方向朝下）：
