eryar

B樣條曲線比Bezier曲線更靈活，它的靈活性來自于你對基函數(shù)靈活地控制。我將對B樣條的各組成部分進(jìn)行講解，首先講一下控制頂點(diǎn)（Control Points）。

Control Points 控制頂點(diǎn)

Bezier曲線的控制頂點(diǎn)對整條曲線都有影響，即改變某一頂點(diǎn)的位置，對整條曲線都有影響，因而Bezier曲線不具有局部修改性。

由于靈活性的緣故，你可以對B樣條設(shè)置任意數(shù)量的控制頂點(diǎn)，也可以確定各控制頂點(diǎn)的影響范圍。

Degree and Order 次數(shù)和階數(shù)

多項(xiàng)式曲線時(shí)，曲線的次數(shù)是由多項(xiàng)式中變量指數(shù)最高項(xiàng)確定。Bezier曲線時(shí)，曲線的次數(shù)由控制頂點(diǎn)數(shù)N確定，即N個(gè)控制頂點(diǎn)的曲線的次數(shù)是（N-1）次。基于這一點(diǎn)，我將引入一些新的術(shù)語來討論曲線的次數(shù)和階數(shù)，即階數(shù)（Order）由設(shè)計(jì)值k確定，次數(shù)（Degree）則為（k-1）。

B樣條把控制頂點(diǎn)數(shù)N與曲線的次數(shù)和控制頂點(diǎn)影響范圍解耦。再抽象點(diǎn)說，曲線上的點(diǎn)只受一些控制頂點(diǎn)的影響，而不是任意控制頂點(diǎn)。或者說每個(gè)控制頂點(diǎn)只影響曲線上的一部分點(diǎn)的值。這就有意思啦，因?yàn)槟銓η€有了局部修改的權(quán)力。你可用16個(gè)控制頂點(diǎn)定義一條曲線，但是它的階數(shù)為4。如圖4.1所示，移動一個(gè)控制頂點(diǎn)只會影響曲線上的一部分。若要用Bezier曲線來實(shí)現(xiàn)，就只能是把幾個(gè)Bezier曲線拼接啦。

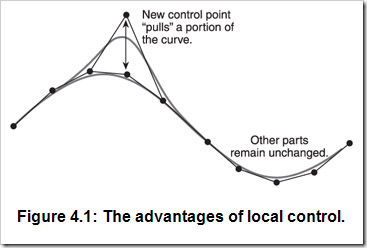
我已經(jīng)講到了術(shù)語階數(shù)（Order）、次數(shù)（Degree），及控制頂點(diǎn)對曲線區(qū)間的影響，但是并沒有講到具體是怎樣影響的。使用Bezier曲線時(shí)，沒有任何的機(jī)制來限制影響的區(qū)間，因?yàn)槿我庖粋€(gè)控制頂點(diǎn)的改變都會影響到曲線上的每個(gè)點(diǎn)。B樣條給你更多的控制，正是由于有節(jié)點(diǎn)向量（Knot Vectors）的機(jī)制。

Knot Vectors 節(jié)點(diǎn)向量

節(jié)點(diǎn)向量的目的就是描述控制頂點(diǎn)的影響范圍。想象一下你想畫一個(gè)有五個(gè)控制頂點(diǎn)的三階曲線，每個(gè)控制頂點(diǎn)只會影響到參數(shù)區(qū)間上的曲線的一小部分。你可以描述任意一個(gè)控制頂點(diǎn)的影響范圍為：[t₀, t₃], [t ₁, t₄], [t₂, t₅], [t₃, t₆], [t₄, t₇]。也可以在一個(gè)單一序列中緊湊的寫成：[t₀ t₁ t₂ t₃ t₄ t₅ t₆ t₇]。這就是節(jié)點(diǎn)向量。圖4.3所示為正式地表示了節(jié)點(diǎn)向量的影響范圍：

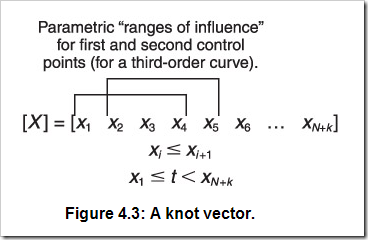
還可以從本例中推出幾個(gè)更普遍的結(jié)論。首先，一個(gè)節(jié)點(diǎn)向量必須有N+k個(gè)元素；其次，節(jié)點(diǎn)向量必須是單調(diào)遞增的。即每個(gè)節(jié)點(diǎn)向量的元素必須比前一個(gè)大或相等。單調(diào)遞增的區(qū)間可以是任意的，當(dāng)然也可以是[0，1]。下面是三個(gè)節(jié)點(diǎn)向量的例子。注意第二個(gè)節(jié)點(diǎn)向量和第三個(gè)在功能上相同，即用它們將會生成相同的曲線：

[X] = [3 4 5 6 7 8]

[X] = [1 2 3 4 5 6 7 8]

[X] = [0.125 0.25 0.375 0.5 0.625 0.75 0.875 1.0]

本書中大部分情況下將會使用整型的節(jié)點(diǎn)向量值，如第二種，因?yàn)檫@樣解釋起來要簡單些。而在程序代碼中，我將使用單位化后的節(jié)點(diǎn)向量，因?yàn)楫?dāng)參數(shù)區(qū)間為[0，1]時(shí)，考慮不同的范圍要簡單些。這兩種情況產(chǎn)生的曲線沒什么不同。

通常喜歡按節(jié)點(diǎn)向量是否均勻分布把節(jié)點(diǎn)向量分為均勻節(jié)點(diǎn)向量和非均勻節(jié)點(diǎn)向量。各舉例如下：

• [X] = [1 2 3 4 5 6] (uniform)

• [X] = [1 3 5 7 9 11] (uniform)

• [X] = [1 2 2 3 3 4] (nonuniform)

• [X] = [1 2 3 3 4 5] (nonuniform)

節(jié)點(diǎn)向量還有兩種類型：開放（Open）和周期性的（Periodic）。

至此為止，你已經(jīng)知道創(chuàng)建B樣條曲線的所有內(nèi)容，除了B樣條的基函數(shù)。知道一系列控制頂點(diǎn)可以用來定義曲線；知道可以用階數(shù)及其相應(yīng)的次數(shù)來描述曲線的屬性；知道節(jié)點(diǎn)向量的機(jī)制，控制頂點(diǎn)是怎樣來影響曲線的。你還需要一個(gè)基本的部分，即把上面所有組合在一起來畫些東西，這就是基函數(shù)（the Basis Function）。

B樣條基函數(shù) B-Spline Basis Functions

在第三章講Bezier曲線時(shí)，生活要簡單的多。Bezier曲線的Bernstein基函數(shù)只是控制頂點(diǎn)的函數(shù)?，F(xiàn)在，有了更多的靈活性，但是需要關(guān)注的就更多。（能力越大，責(zé)任越大。）除了控制頂點(diǎn)以外，B樣條基函數(shù)還需要解釋曲線的次數(shù)，還有由節(jié)點(diǎn)矢量定義的區(qū)間。這個(gè)基函數(shù)不是由Bernstein多項(xiàng)式定義的，而是由Cox-de Boor遞歸公式定義的。這個(gè)著名的遞推公式的發(fā)現(xiàn)是B樣條理論的最重要的進(jìn)展。

[eryar:個(gè)人認(rèn)為公式中第一個(gè)下標(biāo)i是控制頂點(diǎn)的序號，第二個(gè)下標(biāo)是階數(shù)。]

B樣條基的性質(zhì)：

1. 遞推性。由遞推公式可以表明；
2. 局部支承性。局部支承性表明B樣條基是定義在整個(gè)參數(shù)軸上，但僅在支承區(qū)間上有大于零的值，在這個(gè)區(qū)間外均為零。B樣條由其支承區(qū)間內(nèi)的所有節(jié)點(diǎn)決定。
3. 規(guī)范性。

    

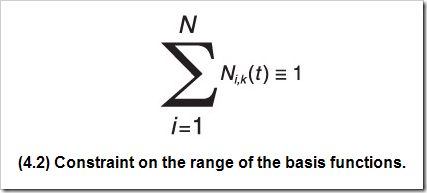
4. 可微性。在節(jié)點(diǎn)區(qū)間內(nèi)部是無限次可微的。

遞推公式的幾何意義可以歸結(jié)為：移位、升階、線性組合。

這些公式初看起來很嚇人，其實(shí)不然，只要你理解它們都是做什么用的。畫Bezier曲線時(shí)，可以根據(jù)Bernstein基函數(shù)很容易就推出一個(gè)基函數(shù)。現(xiàn)在必須根據(jù)階數(shù)來遞推去找到基函數(shù)。從一階基函數(shù)開始推導(dǎo)，因?yàn)楸阌趫D示和舉例。

想像一下我想用四個(gè)控制頂點(diǎn)畫一個(gè)四階三次曲線，我選擇節(jié)點(diǎn)矢量為[X] = [0, 0, 0, 0, 1, 1, 1, 1]。在繼續(xù)后面內(nèi)容之前，用圖4.3中的術(shù)語來考慮一下這個(gè)節(jié)點(diǎn)矢量。這個(gè)節(jié)點(diǎn)矢量讓每個(gè)控制頂點(diǎn)的改變都會影響到整條曲線，聽起來很耳熟？

根據(jù)遞推公式，一階（零次）B樣條的結(jié)果為（此時(shí)階數(shù)k=4，節(jié)點(diǎn)矢量為：[0 0 0 0 1 1 1 1].）：

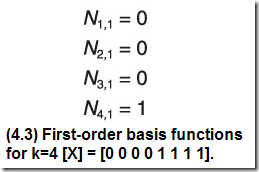
基函數(shù)的圖像為：

將兩個(gè)一階B樣條代入公式即可得到二階B樣條基函數(shù)。推導(dǎo)出方程為：

圖形顯示為：

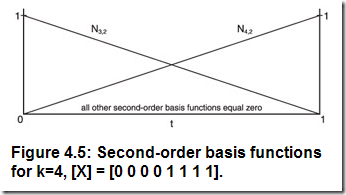
重復(fù)這幾步可以得到三階、四階B樣條基函數(shù)的方程和圖形，如下所示：

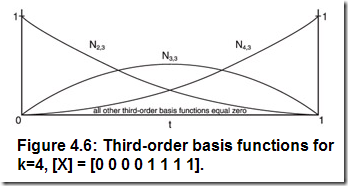
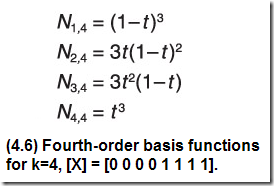
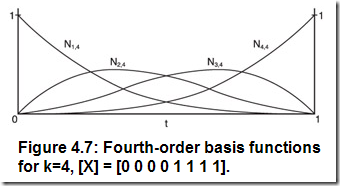
四階B樣條基函數(shù)就是四階、三次曲線所需要的基函數(shù)。這些基函數(shù)畫在一起在圖4.7中，看起來是不是有點(diǎn)眼熟？

正如你所看到的，這些基函數(shù)和第三章中的Bernstein基函數(shù)一模一樣。在第三章中我也提到過，Bezier曲線可以認(rèn)為是B樣條曲線的一個(gè)特例，這里就是證明。通過合適的節(jié)點(diǎn)矢量和次數(shù)，你可以把Bezier曲線看成是更通用的B樣條曲線的特例。這里的節(jié)點(diǎn)矢量選擇的為每個(gè)控制頂點(diǎn)的改變都會影響到整條曲線，次數(shù)也是匹配Bezier曲線的次數(shù)而設(shè)置的。我將在講述不同類型的節(jié)點(diǎn)矢量時(shí)詳談。

上面那些概念都是B樣條曲線的重要組成部分，還有一個(gè)更重的部分。

B樣條曲線方程 The B-Spline Curve Equation

你已經(jīng)有了一系列的基函數(shù)及怎么確定曲線的次數(shù)。如下方程所示為B樣條曲線方程。

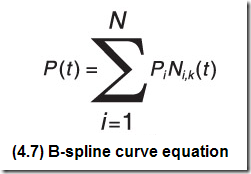
這個(gè)方程和Bezier曲線的方程非常相似。這里基函數(shù)的序列主要用來確定曲線的次數(shù)，基函數(shù)用參數(shù)t定義了每個(gè)控制頂點(diǎn)的影響區(qū)間。只要有了相應(yīng)的基函數(shù)，曲線上的點(diǎn)就可以簡單的表示為所有的控制頂點(diǎn)在給定參數(shù)值t處的權(quán)重的總和。只是現(xiàn)在有些控制頂點(diǎn)的權(quán)重可能是0。

目前為止，你已經(jīng)有了畫出B樣條曲線的所有基礎(chǔ)知識。我也遺露了很多細(xì)節(jié)，最重要的細(xì)節(jié)是節(jié)點(diǎn)矢量部分。既然已經(jīng)掌握了所有基礎(chǔ)知識點(diǎn)，現(xiàn)在回去講解一下細(xì)節(jié)。