A*在游戲?qū)ぢ匪惴ɡ锸褂煤軓V，可是感覺很多介紹它的文章故意讓人看不懂。
仔細看了看gamedev.net的一片文章(
A* Pathfinding for Beginners
http://www.gamedev.net/reference/articles/article2003.asp
)，對A*更了解了一點，寫點東西記錄一下。
A*是一種啟發(fā)式的算法，所謂的"啟發(fā)式"，就是對每一個搜索的位置進行評估，也就是把找的位置離目標(biāo)的距離當(dāng)成找點的一個依據(jù)，然后猜測這個點是否最佳("啟發(fā)式"就是猜測)。
為了找到最佳的那個點
可以規(guī)定：
G = 從起點，沿著產(chǎn)生的路徑，移動到網(wǎng)格上指定方格的距離。
H = 從網(wǎng)格上那個方格移動到終點B的預(yù)估移動距離。
F = G + H
F最小的點可以認為是該選的點。
引用一下原文的翻譯：
我們令水平或者垂直移動的耗費為10，對角線方向耗費為14。我們?nèi)∵@些值是因為沿對角線的距離是沿水平或垂直移動耗費的的根號2（別怕），或者約1.414倍。為了簡化，我們用10和14近似。比例基本正確，同時我們避免了求根運算和小數(shù)。
既然我們在計算沿特定路徑通往某個方格的G值，求值的方法就是取它父節(jié)點的G值，然后依照它相對父節(jié)點是對角線方向或者直角方向(非對角線)，分別增加14和10。例子中這個方法的需求會變得更多，因為我們從起點方格以外獲取了不止一個方格。
H值可以用不同的方法估算。我們這里使用的方法被稱為曼哈頓方法，它計算從當(dāng)前格到目的格之間水平和垂直的方格的數(shù)量總和，忽略對角線方向。然后把結(jié)果乘以10。這被成為曼哈頓方法是因為它看起來像計算城市中從一個地方到另外一個地方的街區(qū)數(shù)，在那里你不能沿對角線方向穿過街區(qū)。很重要的一點，我們忽略了一切障礙物。這是對剩余距離的一個估算，而非實際值，這也是這一方法被稱為啟發(fā)式的原因。想知道更多？你可以在這里找到方程和額外的注解。
第一步搜索的結(jié)果可以在下面的圖表中看到。F,G和H的評分被寫在每個方格里。正如在緊挨起始格右側(cè)的方格所表示的，F(xiàn)被打印在左上角，G在左下角，H則在右下角。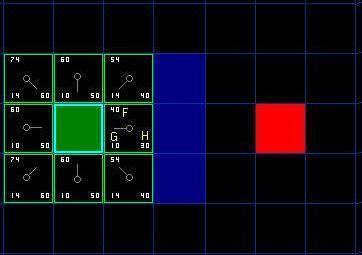
引用一下原文的翻譯：
我們做如下操作開始搜索：
???1，從點A開始，并且把它作為待處理點存入一個“開啟列表”。開啟列表就像一張購物清單。盡管現(xiàn)在列表里只有一個元素，但以后就會多起來。你的路徑可能會通過它包含的方格，也可能不會。基本上，這是一個待檢查方格的列表。
???2，尋找起點周圍所有可到達或者可通過的方格，跳過有墻，水，或其他無法通過地形的方格。也把他們加入開啟列表。為所有這些方格保存點A作為“父方格”。當(dāng)我們想描述路徑的時候，父方格的資料是十分重要的。后面會解釋它的具體用途。
???3，從開啟列表中刪除點A，把它加入到一個“關(guān)閉列表”，列表中保存所有不需要再次檢查的方格。
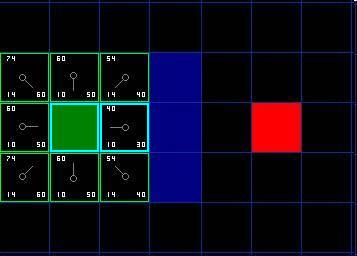
為了繼續(xù)搜索，我們簡單的從開啟列表中選擇F值最低的方格。然后，對選中的方格做如下處理：
???4，把它從開啟列表中刪除，然后添加到關(guān)閉列表中。
???5，檢查所有相鄰格子。跳過那些已經(jīng)在關(guān)閉列表中的或者不可通過的(有墻，水的地形，或者其他無法通過的地形)，把他們添加進開啟列表，如果他們還不在里面的話。把選中的方格作為新的方格的父節(jié)點。
???6，如果某個相鄰格已經(jīng)在開啟列表里了，檢查現(xiàn)在的這條路徑是否更好。換句話說，檢查如果我們用新的路徑到達它的話，G值是否會更低一些。如果不是，那就什么都不做。
??????另一方面，如果新的G值更低，那就把相鄰方格的父節(jié)點改為目前選中的方格（在上面的圖表中，把箭頭的方向改為指向這個方格）。最后，重新計算F和G的值。如果這看起來不夠清晰，你可以看下面的圖示。
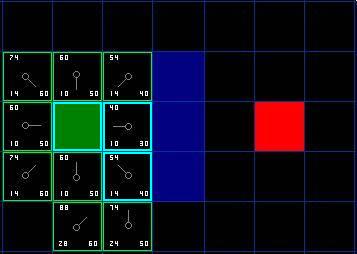
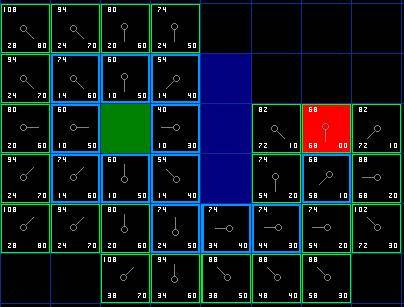
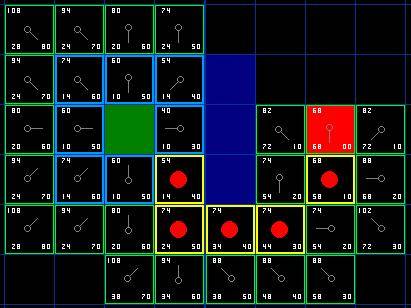
這樣就可以找到最佳路徑了。