散列表(Hash table,也叫哈希表),是根據(jù)關(guān)鍵碼值(Key value)而直接進(jìn)行訪問(wèn)的數(shù)據(jù)結(jié)構(gòu)。也就是說(shuō),它通過(guò)把關(guān)鍵碼值映射到表中一個(gè)位置來(lái)訪問(wèn)記錄,以加快查找的速度。這個(gè)映射函數(shù)叫做散列函數(shù),存放記錄的數(shù)組叫做散列表。
哈希表算法-哈希表的構(gòu)造方法
1、直接定址法
例如:有一個(gè)從1到100歲的人口數(shù)字統(tǒng)計(jì)表,其中,年齡作為關(guān)鍵字,哈希函數(shù)取關(guān)鍵字自身。
但這種方法效率不高,時(shí)間復(fù)雜度是O(1),空間復(fù)雜度是O(n),n是關(guān)鍵字的個(gè)數(shù)
 哈希表算法
哈希表算法
2、數(shù)字分析法
有學(xué)生的生日數(shù)據(jù)如下:
年.月.日
75.10.03
75.11.23
76.03.02
76.07.12
75.04.21
76.02.15
...
經(jīng)分析,第一位,第二位,第三位重復(fù)的可能性大,取這三位造成沖突的機(jī)會(huì)增加,所以盡量不取前三位,取后三位比較好。
3、平方取中法
取關(guān)鍵字平方后的中間幾位為哈希地址。
4、折疊法
將關(guān)鍵字分割成位數(shù)相同的幾部分(最后一部分的位數(shù)可以不同),然后取這幾部分的疊加和(舍去進(jìn)位)作為哈希地址,這方法稱為折疊法。
例如:每一種西文圖書都有一個(gè)國(guó)際標(biāo)準(zhǔn)圖書編號(hào),它是一個(gè)10位的十進(jìn)制數(shù)字,若要以它作關(guān)鍵字建立一個(gè)哈希表,當(dāng)館藏書種類不到10,000時(shí),可采用此法構(gòu)造一個(gè)四位數(shù)的哈希函數(shù)。如果一本書的編號(hào)為0-442-20586-4,則:
 哈希表算法
哈希表算法
5、除留余數(shù)法
取關(guān)鍵字被某個(gè)不大于哈希表表長(zhǎng)m的數(shù)p除后所得余數(shù)為哈希地址。
H(key)=key MOD p (p<=m)
6、隨機(jī)數(shù)法
選擇一個(gè)隨機(jī)函數(shù),取關(guān)鍵字的隨機(jī)函數(shù)值為它的哈希地址,即
H(key)=random(key) ,其中random為隨機(jī)函數(shù)。通常用于關(guān)鍵字長(zhǎng)度不等時(shí)采用此法。
5、除留余數(shù)法
取關(guān)鍵字被某個(gè)不大于哈希表表長(zhǎng)m的數(shù)p除后所得余數(shù)為哈希地址。
H(key)=key MOD p (p<=m)
6、隨機(jī)數(shù)法
選擇一個(gè)隨機(jī)函數(shù),取關(guān)鍵字的隨機(jī)函數(shù)值為它的哈希地址,即
H(key)=random(key) ,其中random為隨機(jī)函數(shù)。通常用于關(guān)鍵字長(zhǎng)度不等時(shí)采用此法。
5、除留余數(shù)法
取關(guān)鍵字被某個(gè)不大于哈希表表長(zhǎng)m的數(shù)p除后所得余數(shù)為哈希地址。
H(key)=key MOD p (p<=m)
6、隨機(jī)數(shù)法
選擇一個(gè)隨機(jī)函數(shù),取關(guān)鍵字的隨機(jī)函數(shù)值為它的哈希地址,即
H(key)=random(key) ,其中random為隨機(jī)函數(shù)。通常用于關(guān)鍵字長(zhǎng)度不等時(shí)采用此法。
處理沖突的方法 通常有兩類方法處理沖突:開(kāi)放定址(Open Addressing)法和拉鏈(Chaining)法。前者是將所有結(jié)點(diǎn)均存放在散列表T[0..m-1]中;后者通常是將互為同義詞的結(jié)點(diǎn)鏈成一個(gè)單鏈表,而將此鏈表的頭指針?lè)旁谏⒘斜鞹[0..m-1]中。1、開(kāi)放定址法(1)開(kāi)放地址法解決沖突的方法 用開(kāi)放定址法解決沖突的做法是:當(dāng)沖突發(fā)生時(shí),使用某種探查(亦稱探測(cè))技術(shù)在散列表中形成一個(gè)探查(測(cè))序列。沿此序列逐個(gè)單元地查找,直到找到給定 的關(guān)鍵字,或者碰到一個(gè)開(kāi)放的地址(即該地址單元為空)為止(若要插入,在探查到開(kāi)放的地址,則可將待插入的新結(jié)點(diǎn)存人該地址單元)。查找時(shí)探查到開(kāi)放的 地址則表明表中無(wú)待查的關(guān)鍵字,即查找失敗。注意:①用開(kāi)放定址法建立散列表時(shí),建表前須將表中所有單元(更嚴(yán)格地說(shuō),是指單元中存儲(chǔ)的關(guān)鍵字)置空。②空單元的表示與具體的應(yīng)用相關(guān)。【例】關(guān)鍵字均為非負(fù)數(shù)時(shí),可用"-1"來(lái)表示空單元,而關(guān)鍵字為字符串時(shí),空單元應(yīng)是空串。總之:應(yīng)該用一個(gè)不會(huì)出現(xiàn)的關(guān)鍵字來(lái)表示空單元。(2)開(kāi)放地址法的一般形式開(kāi)放定址法的一般形式為: hi=(h(key)+di)%m 1≤i≤m-1 其中: ①h(key)為散列函數(shù),di為增量序列,m為表長(zhǎng)。 ②h(key)是初始的探查位置,后續(xù)的探查位置依次是hl,h2,…,hm-1,即h(key),hl,h2,…,hm-1形成了一個(gè)探查序列。 ③若令開(kāi)放地址一般形式的i從0開(kāi)始,并令d0=0,則h0=h(key),則有:hi=(h(key)+di)%m 0≤i≤m-1 探查序列可簡(jiǎn)記為hi(0≤i≤m-1)。(3)開(kāi)放地址法堆裝填因子的要求 開(kāi)放定址法要求散列表的裝填因子α≤l,實(shí)用中取α為0.5到0.9之間的某個(gè)值為宜。(4)形成探測(cè)序列的方法 按照形成探查序列的方法不同,可將開(kāi)放定址法區(qū)分為線性探查法、二次探查法、雙重散列法等。①線性探查法(Linear Probing)該方法的基本思想是:將散列表T[0..m-1]看成是一個(gè)循環(huán)向量,若初始探查的地址為d(即h(key)=d),則最長(zhǎng)的探查序列為:d,d+l,d+2,…,m-1,0,1,…,d-1 即:探查時(shí)從地址d開(kāi)始,首先探查T[d],然后依次探查T[d+1],…,直到T[m-1],此后又循環(huán)到T[0],T[1],…,直到探查到T[d-1]為止。探查過(guò)程終止于三種情況: (1)若當(dāng)前探查的單元為空,則表示查找失敗(若是插入則將key寫入其中); (2)若當(dāng)前探查的單元中含有key,則查找成功,但對(duì)于插入意味著失敗; (3)若探查到T[d-1]時(shí)仍未發(fā)現(xiàn)空單元也未找到key,則無(wú)論是查找還是插入均意味著失敗(此時(shí)表滿)。利用開(kāi)放地址法的一般形式,線性探查法的探查序列為:hi=(h(key)+i)%m 0≤i≤m-1 //即di=i利用線性探測(cè)法構(gòu)造散列表【例9.1】已知一組關(guān)鍵字為(26,36,41,38,44,15,68,12,06,51),用除余法構(gòu)造散列函數(shù),用線性探查法解決沖突構(gòu)造這組關(guān)鍵字的散列表。解答:為了減少?zèng)_突,通常令裝填因子α 由除余法的散列函數(shù)計(jì)算出的上述關(guān)鍵字序列的散列地址為(0,10,2,12,5,2,3,12,6,12)。 前5個(gè)關(guān)鍵字插入時(shí),其相應(yīng)的地址均為開(kāi)放地址,故將它們直接插入T[0],T[10),T[2],T[12]和T[5]中。 當(dāng)插入第6個(gè)關(guān)鍵字15時(shí),其散列地址2(即h(15)=15%13=2)已被關(guān)鍵字41(15和41互為同義詞)占用。故探查h1=(2+1)%13=3,此地址開(kāi)放,所以將15放入T[3]中。 當(dāng)插入第7個(gè)關(guān)鍵字68時(shí),其散列地址3已被非同義詞15先占用,故將其插入到T[4]中。 當(dāng)插入第8個(gè)關(guān)鍵字12時(shí),散列地址12已被同義詞38占用,故探查hl=(12+1)%13=0,而T[0]亦被26占用,再探查h2=(12+2)%13=1,此地址開(kāi)放,可將12插入其中。 類似地,第9個(gè)關(guān)鍵字06直接插入T[6]中;而最后一個(gè)關(guān)鍵字51插人時(shí),因探查的地址12,0,1,…,6均非空,故51插入T[7]中。 構(gòu)造散列表的具體過(guò)程【參見(jiàn)動(dòng)畫演示】聚集或堆積現(xiàn)象用線性探查法解決沖突時(shí),當(dāng)表中i,i+1,…,i+k的位置上已有結(jié)點(diǎn)時(shí),一個(gè)散列地址為i,i+1,…,i+k+1的結(jié)點(diǎn)都將插入在位置i+k+1 上。把這種散列地址不同的結(jié)點(diǎn)爭(zhēng)奪同一個(gè)后繼散列地址的現(xiàn)象稱為聚集或堆積(Clustering)。這將造成不是同義詞的結(jié)點(diǎn)也處在同一個(gè)探查序列之 中,從而增加了探查序列的長(zhǎng)度,即增加了查找時(shí)間。若散列函數(shù)不好或裝填因子過(guò)大,都會(huì)使堆積現(xiàn)象加劇。【例】上例中,h(15)=2,h(68)=3,即15和68不是同義詞。但由于處理15和同義詞41的沖突時(shí),15搶先占用了T[3],這就使得插入68時(shí),這兩個(gè)本來(lái)不應(yīng)該發(fā)生沖突的非同義詞之間也會(huì)發(fā)生沖突。 為了減少堆積的發(fā)生,不能像線性探查法那樣探查一個(gè)順序的地址序列(相當(dāng)于順序查找),而應(yīng)使探查序列跳躍式地散列在整個(gè)散列表中。②二次探查法(Quadratic Probing) 二次探查法的探查序列是:hi=(h(key)+i*i)%m 0≤i≤m-1 //即di=i2即探查序列為d=h(key),d+12,d+22,…,等。 該方法的缺陷是不易探查到整個(gè)散列空間。③雙重散列法(Double Hashing) 該方法是開(kāi)放定址法中最好的方法之一,它的探查序列是:hi=(h(key)+i*h1(key))%m 0≤i≤m-1 //即di=i*h1(key) 即探查序列為:d=h(key),(d+h1(key))%m,(d+2h1(key))%m,…,等。 該方法使用了兩個(gè)散列函數(shù)h(key)和h1(key),故也稱為雙散列函數(shù)探查法。注意:定義h1(key)的方法較多,但無(wú)論采用什么方法定義,都必須使h1(key)的值和m互素,才能使發(fā)生沖突的同義詞地址均勻地分布在整個(gè)表中,否則可能造成同義詞地址的循環(huán)計(jì)算。【例】若m為素?cái)?shù),則h1(key)取1到m-1之間的任何數(shù)均與m互素,因此,我們可以簡(jiǎn)單地將它定義為:h1(key)=key%(m-2)+1【例】對(duì)例9.1,我們可取h(key)=key%13,而h1(key)=key%11+1。【例】若m是2的方冪,則h1(key)可取1到m-1之間的任何奇數(shù)。2、拉鏈法(1)拉鏈法解決沖突的方法 拉鏈法解決沖突的做法是:將所有關(guān)鍵字為同義詞的結(jié)點(diǎn)鏈接在同一個(gè)單鏈表中。若選定的散列表長(zhǎng)度為m,則可將散列表定義為一個(gè)由m個(gè)頭指針組成的指針數(shù) 組T[0..m-1]。凡是散列地址為i的結(jié)點(diǎn),均插入到以T[i]為頭指針的單鏈表中。T中各分量的初值均應(yīng)為空指針。在拉鏈法中,裝填因子α可以大于 1,但一般均取α≤1。【例9.2】已知一組關(guān)鍵字和選定的散列函數(shù)和例9.1相同,用拉鏈法解決沖突構(gòu)造這組關(guān)鍵字的散列表。解答:不妨和例9.1類似,取表長(zhǎng)為13,故散列函數(shù)為h(key)=key%13,散列表為T[0..12]。注意:當(dāng)把h(key)=i的關(guān)鍵字插入第i個(gè)單鏈表時(shí),既可插入在鏈表的頭上,也可以插在鏈表的尾上。這是因?yàn)楸仨毚_定key不在第i個(gè)鏈表時(shí),才能將它插入 表中,所以也就知道鏈尾結(jié)點(diǎn)的地址。若采用將新關(guān)鍵字插入鏈尾的方式,依次把給定的這組關(guān)鍵字插入表中,則所得到的散列表如下圖所示。 具體構(gòu)造過(guò)程【參見(jiàn)動(dòng)畫演示】。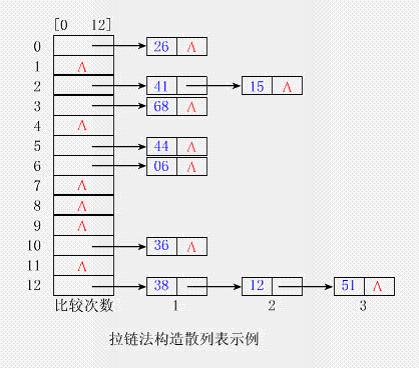 (2)拉鏈法的優(yōu)點(diǎn) 與開(kāi)放定址法相比,拉鏈法有如下幾個(gè)優(yōu)點(diǎn):(1)拉鏈法處理沖突簡(jiǎn)單,且無(wú)堆積現(xiàn)象,即非同義詞決不會(huì)發(fā)生沖突,因此平均查找長(zhǎng)度較短;(2)由于拉鏈法中各鏈表上的結(jié)點(diǎn)空間是動(dòng)態(tài)申請(qǐng)的,故它更適合于造表前無(wú)法確定表長(zhǎng)的情況;(3)開(kāi)放定址法為減少?zèng)_突,要求裝填因子α較小,故當(dāng)結(jié)點(diǎn)規(guī)模較大時(shí)會(huì)浪費(fèi)很多空間。而拉鏈法中可取α≥1,且結(jié)點(diǎn)較大時(shí),拉鏈法中增加的指針域可忽略不計(jì),因此節(jié)省空間;(4)在用拉鏈法構(gòu)造的散列表中,刪除結(jié)點(diǎn)的操作易于實(shí)現(xiàn)。只要簡(jiǎn)單地刪去鏈表上相應(yīng)的結(jié)點(diǎn)即可。而對(duì)開(kāi)放地址法構(gòu)造的散列表,刪除結(jié)點(diǎn)不能簡(jiǎn)單地將 被刪結(jié)點(diǎn)的空間置為空,否則將截?cái)嘣谒筇钊松⒘斜淼耐x詞結(jié)點(diǎn)的查找路徑。這是因?yàn)楦鞣N開(kāi)放地址法中,空地址單元(即開(kāi)放地址)都是查找失敗的條件。 因此在用開(kāi)放地址法處理沖突的散列表上執(zhí)行刪除操作,只能在被刪結(jié)點(diǎn)上做刪除標(biāo)記,而不能真正刪除結(jié)點(diǎn)。(3)拉鏈法的缺點(diǎn) 拉鏈法的缺點(diǎn)是:指針需要額外的空間,故當(dāng)結(jié)點(diǎn)規(guī)模較小時(shí),開(kāi)放定址法較為節(jié)省空間,而若將節(jié)省的指針空間用來(lái)擴(kuò)大散列表的規(guī)模,可使裝填因子變小,這又減少了開(kāi)放定址法中的沖突,從而提高平均查找速度。
(2)拉鏈法的優(yōu)點(diǎn) 與開(kāi)放定址法相比,拉鏈法有如下幾個(gè)優(yōu)點(diǎn):(1)拉鏈法處理沖突簡(jiǎn)單,且無(wú)堆積現(xiàn)象,即非同義詞決不會(huì)發(fā)生沖突,因此平均查找長(zhǎng)度較短;(2)由于拉鏈法中各鏈表上的結(jié)點(diǎn)空間是動(dòng)態(tài)申請(qǐng)的,故它更適合于造表前無(wú)法確定表長(zhǎng)的情況;(3)開(kāi)放定址法為減少?zèng)_突,要求裝填因子α較小,故當(dāng)結(jié)點(diǎn)規(guī)模較大時(shí)會(huì)浪費(fèi)很多空間。而拉鏈法中可取α≥1,且結(jié)點(diǎn)較大時(shí),拉鏈法中增加的指針域可忽略不計(jì),因此節(jié)省空間;(4)在用拉鏈法構(gòu)造的散列表中,刪除結(jié)點(diǎn)的操作易于實(shí)現(xiàn)。只要簡(jiǎn)單地刪去鏈表上相應(yīng)的結(jié)點(diǎn)即可。而對(duì)開(kāi)放地址法構(gòu)造的散列表,刪除結(jié)點(diǎn)不能簡(jiǎn)單地將 被刪結(jié)點(diǎn)的空間置為空,否則將截?cái)嘣谒筇钊松⒘斜淼耐x詞結(jié)點(diǎn)的查找路徑。這是因?yàn)楦鞣N開(kāi)放地址法中,空地址單元(即開(kāi)放地址)都是查找失敗的條件。 因此在用開(kāi)放地址法處理沖突的散列表上執(zhí)行刪除操作,只能在被刪結(jié)點(diǎn)上做刪除標(biāo)記,而不能真正刪除結(jié)點(diǎn)。(3)拉鏈法的缺點(diǎn) 拉鏈法的缺點(diǎn)是:指針需要額外的空間,故當(dāng)結(jié)點(diǎn)規(guī)模較小時(shí),開(kāi)放定址法較為節(jié)省空間,而若將節(jié)省的指針空間用來(lái)擴(kuò)大散列表的規(guī)模,可使裝填因子變小,這又減少了開(kāi)放定址法中的沖突,從而提高平均查找速度。本文轉(zhuǎn)自:http://bbs.csdn.net/topics/320198804
http://www.cnblogs.com/jiewei915/archive/2010/08/09/1796042.html
posted on 2012-11-21 14:22
王海光 閱讀(729)
評(píng)論(0) 編輯 收藏 引用 所屬分類:
算法