本文轉(zhuǎn)自：http://www.cnblogs.com/jillzhang/archive/2006/11/02/547679.html

哈希表和哈希函數(shù)是大學(xué)數(shù)據(jù)結(jié)構(gòu)中的課程，實(shí)際開發(fā)中我們經(jīng)常用到Hashtable這種結(jié)構(gòu)，當(dāng)遇到鍵-值對(duì)存儲(chǔ)，采用Hashtable比ArrayList查找的性能高。為什么呢？我們?cè)谙硎芨咝阅艿耐瑫r(shí)，需要付出什么代價(jià)(這幾天看紅頂商人胡雪巖，經(jīng)典臺(tái)詞：在你享受這之前，必須受別人吃不了的苦，忍受別人受不了的屈辱)，那么使用Hashtable是否就是一樁無本萬利的買賣呢？就此疑問，做以下分析，希望能拋磚引玉。
1)hash它為什么對(duì)于鍵-值查找性能高
學(xué)過數(shù)據(jù)結(jié)構(gòu)的，都應(yīng)該曉得，線性表和樹中，記錄在結(jié)構(gòu)中的相對(duì)位置是隨機(jī)的，記錄和關(guān)鍵字之間不存在明確的關(guān)系，因此在查找記錄的時(shí)候，需要進(jìn)行一系列的關(guān)鍵字比較，這種查找方式建立在比較的基礎(chǔ)之上，在.net中(Array,ArrayList,List)這些集合結(jié)構(gòu)采用了上面的存儲(chǔ)方式。
比如，現(xiàn)在我們有一個(gè)班同學(xué)的數(shù)據(jù)，包括姓名，性別，年齡，學(xué)號(hào)等。假如數(shù)據(jù)有

姓名	性別	年齡	學(xué)號(hào)
張三	男	15	1
李四	女	14	2
王五	男	14	3

 

假如，我們按照姓名來查找，假設(shè)查找函數(shù)FindByName(string name);
1)查找“張三”
只需在第一行匹配一次。
2)查找"王五"
   在第一行匹配，失敗，
   在第二行匹配，失敗，
   在第三行匹配，成功
上面兩種情況，分別分析了最好的情況，和最壞的情況，那么平均查找次數(shù)應(yīng)該為 (1+3)/2=2次，即平均查找次數(shù)為(記錄總數(shù)+1)的1/2。
盡管有一些優(yōu)化的算法，可以使查找排序效率增高，但是復(fù)雜度會(huì)保持在log2n的范圍之內(nèi)。
如何更更快的進(jìn)行查找呢？我們所期望的效果是一下子就定位到要找記錄的位置之上，這時(shí)候時(shí)間復(fù)雜度為1，查找最快。如果我們事先為每條記錄編一個(gè)序號(hào)，然后讓他們按號(hào)入位，我們又知道按照什么規(guī)則對(duì)這些記錄進(jìn)行編號(hào)的話，如果我們?cè)俅尾檎夷硞€(gè)記錄的時(shí)候，只需要先通過規(guī)則計(jì)算出該記錄的編號(hào)，然后根據(jù)編號(hào)，在記錄的線性隊(duì)列中，就可以輕易的找到記錄了 。
注意，上述的描述包含了兩個(gè)概念，一個(gè)是用于對(duì)學(xué)生進(jìn)行編號(hào)的規(guī)則，在數(shù)據(jù)結(jié)構(gòu)中，稱之為哈希函數(shù)，另外一個(gè)是按照規(guī)則為學(xué)生排列的順序結(jié)構(gòu)，稱之為哈希表。
仍以上面的學(xué)生為例，假設(shè)學(xué)號(hào)就是規(guī)則，老師手上有一個(gè)規(guī)則表，在排座位的時(shí)候也按照這個(gè)規(guī)則來排序，查找李四，首先該教師會(huì)根據(jù)規(guī)則判斷出，李四的編號(hào)為2，就是在座位中的2號(hào)位置，直接走過去，“李四，哈哈，你小子，就是在這！”
看看大體流程:
 
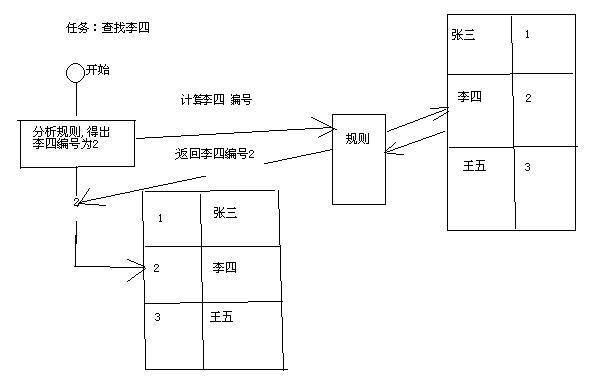
從上面的圖中，可以看出哈希表可以描述為兩個(gè)筒子，一個(gè)筒子用來裝記錄的位置編號(hào)，另外一個(gè)筒子用來裝記錄，另外存在一套規(guī)則，用來表述記錄與編號(hào)之間的聯(lián)系。這個(gè)規(guī)則通常是如何制定的呢？
a)直接定址法:
   我在前一篇文章對(duì)GetHashCode()性能比較的問題中談到，對(duì)于整形的數(shù)據(jù)GetHashCode()函數(shù)返回的就是整形　　　本身，其實(shí)就是基于直接定址的方法，比如有一組0-100的數(shù)據(jù)，用來表示人的年齡
那么，采用直接定址的方法構(gòu)成的哈希表為:

0	1	2	3	4	5
0歲	１歲	２歲	３歲	４歲	５歲

.....
這樣的一種定址方式，簡(jiǎn)單方便，適用于元數(shù)據(jù)能夠用數(shù)字表述或者原數(shù)據(jù)具有鮮明順序關(guān)系的情形。
b)數(shù)字分析法:
  有這樣一組數(shù)據(jù)，用于表述一些人的出生日期

年	月	日
７５	１０	１
７５	１２	１０
７５	０２	１４

分析一下，年和月的第一位數(shù)字基本相同，造成沖突的幾率非常大，而后面三位差別比較大，所以采用后三位
c)平方取中法
　取關(guān)鍵字平方后的中間幾位作為哈希地址
d) 折疊法：
　將關(guān)鍵字分割成位數(shù)相同的幾部分，最后一部分位數(shù)可以不相同，然后去這幾部分的疊加和（取出進(jìn)位）作為哈希地址，比如有這樣的數(shù)據(jù)20-1445-4547-3
可以
        5473
+      4454
+        201
=    10128
取出進(jìn)位1,取0128為哈希地址
e)取余法
取關(guān)鍵字被某個(gè)不大于哈希表表長(zhǎng)m的數(shù)p除后所得余數(shù)為哈希地址。H(key)=key MOD p (p<=m)
f) 隨機(jī)數(shù)法
　選擇一個(gè)隨機(jī)函數(shù)，取關(guān)鍵字的隨機(jī)函數(shù)值為它的哈希地址，即H(key)=random(key) ,其中random為隨機(jī)函數(shù)。通常用于關(guān)鍵字長(zhǎng)度不等時(shí)采用此法。

 

總之，哈希函數(shù)的規(guī)則是：通過某種轉(zhuǎn)換關(guān)系，使關(guān)鍵字適度的分散到指定大小的的順序結(jié)構(gòu)中。越分散，則以后查找的時(shí)間復(fù)雜度越小，空間復(fù)雜度越高。
２)使用hash，我們付出了什么？
hash是一種典型以空間換時(shí)間的算法，比如原來一個(gè)長(zhǎng)度為100的數(shù)組，對(duì)其查找，只需要遍歷且匹配相應(yīng)記錄即可，從空間復(fù)雜度上來看，假如數(shù)組存儲(chǔ)的是byte類型數(shù)據(jù)，那么該數(shù)組占用100byte空間。現(xiàn)在我們采用hash算法，我們前面說的hash必須有一個(gè)規(guī)則，約束鍵與存儲(chǔ)位置的關(guān)系，那么就需要一個(gè)固定長(zhǎng)度的hash表，此時(shí)，仍然是100byte的數(shù)組，假設(shè)我們需要的100byte用來記錄鍵與位置的關(guān)系，那么總的空間為200byte,而且用于記錄規(guī)則的表大小會(huì)根據(jù)規(guī)則，大小可能是不定的，比如在lzw算法中，如果一個(gè)很長(zhǎng)的用于記錄像素的byte數(shù)組，用來記錄位置與鍵關(guān)系的表空間，算法推薦為一個(gè)1２bit能表述的整數(shù)大小，那么足夠長(zhǎng)的像素?cái)?shù)組，如何分散到這樣定長(zhǎng)的表中呢，lzw算法采用的是可變長(zhǎng)編碼，具體會(huì)在深入介紹lzw算法的時(shí)候介紹。
注:hash表最突出的問題在于沖突，就是兩個(gè)鍵值經(jīng)過哈希函數(shù)計(jì)算出來的索引位置很可能相同，這個(gè)問題，下篇文章會(huì)令作闡述。
注:之所以會(huì)簡(jiǎn)單得介紹了hash，是為了更好的學(xué)習(xí)lzw算法，學(xué)習(xí)lzw算法是為了更好的研究gif文件結(jié)構(gòu)，最后，我將詳細(xì)的闡述一下gif文件是如何構(gòu)成的，如何高效操作此種類型文件。

HASH如何處理沖突：

1)沖突是如何產(chǎn)生的？
上文中談到，哈希函數(shù)是指如何對(duì)關(guān)鍵字進(jìn)行編址的規(guī)則，這里的關(guān)鍵字的范圍很廣，可視為無限集，如何保證無限集的原數(shù)據(jù)在編址的時(shí)候不會(huì)出現(xiàn)重復(fù)呢？規(guī)則本身無法實(shí)現(xiàn)這個(gè)目的。舉一個(gè)例子，仍然用班級(jí)同學(xué)做比喻，現(xiàn)有如下同學(xué)數(shù)據(jù)
張三，李四，王五，趙剛，吳露.....
假如我們編址規(guī)則為取姓氏中姓的開頭字母在字母表的相對(duì)位置作為地址，則會(huì)產(chǎn)生如下的哈希表

位置	字母	姓名
0	a
1	b
2	c

 

...

10

L

李四

...

22

W

王五，吳露

..

25

Z

張三，趙剛

我們注意到，灰色背景標(biāo)示的兩行里面，關(guān)鍵字王五，吳露被編到了同一個(gè)位置，關(guān)鍵字張三，趙剛也被編到了同一個(gè)位置。老師再拿號(hào)來找張三，座位上有兩個(gè)人，"你們倆誰是張三？"
2)如何解決沖突問題
既然不能避免沖突，那么如何解決沖突呢，顯然需要附加的步驟。通過這些步驟，以制定更多的規(guī)則來管理關(guān)鍵字集合，通常的辦法有:
a)開放地址法
開放地執(zhí)法有一個(gè)公式:Hi=(H(key)+di) MOD m i=1,2,...,k(k<=m-1)
其中，m為哈希表的表長(zhǎng)。di 是產(chǎn)生沖突的時(shí)候的增量序列。如果di值可能為1,2,3,...m-1，稱線性探測(cè)再散列。
如果di取1，則每次沖突之后，向后移動(dòng)1個(gè)位置.如果di取值可能為1,-1,2,-2,4,-4,9,-9,16,-16,...k*k,-k*k(k<=m/2) 
稱二次探測(cè)再散列。如果di取值可能為偽隨機(jī)數(shù)列。稱偽隨機(jī)探測(cè)再散列。仍然以學(xué)生排號(hào)作為例子，
現(xiàn)有兩名同學(xué)，李四，吳用。李四與吳用事先已排好序，現(xiàn)新來一名同學(xué)，名字叫王五，對(duì)它進(jìn)行編制

10..	....	22	..	..	25
李四..	....	吳用	..	..	25

   趙剛未來之前

10..	..	22	23	25
李四..		吳用	王五

   (a)線性探測(cè)再散列對(duì)趙剛進(jìn)行編址，且di=1

10...	20	22	..	25
李四..	王五	吳用

   (b)二次探測(cè)再散列，且di=-2

1...	10...	22	..	25
王五..	李四..	吳用

   (c)偽隨機(jī)探測(cè)再散列,偽隨機(jī)序列為:5,3,2

b)再哈希法 
當(dāng)發(fā)生沖突時(shí)，使用第二個(gè)、第三個(gè)、哈希函數(shù)計(jì)算地址，直到無沖突時(shí)。缺點(diǎn)：計(jì)算時(shí)間增加。
比如上面第一次按照姓首字母進(jìn)行哈希，如果產(chǎn)生沖突可以按照姓字母首字母第二位進(jìn)行哈希，再?zèng)_突，第三位，直到不沖突為止
c)鏈地址法
將所有關(guān)鍵字為同義詞的記錄存儲(chǔ)在同一線性鏈表中。如下：

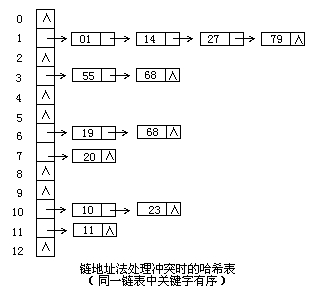
因此這種方法，可以近似的認(rèn)為是筒子里面套筒子
d.建立一個(gè)公共溢出區(qū)
假設(shè)哈希函數(shù)的值域?yàn)閇0,m-1],則設(shè)向量HashTable[0..m-1]為基本表，另外設(shè)立存儲(chǔ)空間向量OverTable[0..v]用以存儲(chǔ)發(fā)生沖突的記錄。
經(jīng)過以上方法，基本可以解決掉hash算法沖突的問題。