[點連通度與邊連通度]

在一個無向連通圖中，如果有一個頂點集合，刪除這個頂點集合，以及這個集合中所有頂點相關聯的邊以后，原圖變成多個連通塊，就稱這個點集為割點集合。一個圖的點連通度的定義為，最小割點集合中的頂點數。

A cut, vertex cut, or separating set of a connected graph G is a set of vertices whose removal renders G disconnected. Theconnectivity or vertex connectivity κ(G) is the size of a smallest vertex cut. A graph is called k-connected or k-vertex-connected if its vertex connectivity is k or greater. A complete graph with n vertices has no cuts at all, but by convention its connectivity is n-1. A vertex cut for two vertices u and v is a set of vertices whose removal from the graph disconnects u and v. The local connectivity κ(u,v) is the size of a smallest vertex cut separating u and v. Local connectivity is symmetric for undirected graphs; that is, κ(u,v)=κ(v,u). Moreover, except for complete graphs, κ(G) equals the minimum of κ(u,v) over all nonadjacent pairs of vertices u,v.

2-connectivity is also called "biconnectivity" and 3-connectivity is also called "triconnectivity".

Analogous concepts can be defined for edges. In the simple case in which cutting a single, specific edge would disconnect the graph, that edge is called a bridge. More generally, the edge cut of G is a group of edges whose total removal renders the graph disconnected. The edge-connectivity λ(G) is the size of a smallest edge cut, and the local edge-connectivity λ(u,v) of two vertices u,v is the size of a smallest edge cut disconnecting u from v. Again, local edge-connectivity is symmetric. A graph is called k-edge-connected if its edge connectivity is k or greater.

類似的，如果有一個邊集合，刪除這個邊集合以后，原圖變成多個連通塊，就稱這個點集為割邊集合。一個圖的邊連通度的定義為，最小割邊集合中的邊數。

[雙連通圖 割點 與橋]

Point Biconnected Component 無向圖點2連通分量與    cut point 割點

Edge Biconnected Component 無向圖邊2連通分量與    bridge 橋

如果一個無向連通圖的點連通度大于1，則稱該圖是點雙連通的(point biconnected)，簡稱雙連通或重連通。一個圖有割點，當且僅當這個圖的點連通度為1，則割點集合的唯一元素被稱為割點(cut point)，又叫關節點(articulation point)。

如果一個無向連通圖的邊連通度大于1，則稱該圖是邊雙連通的(edge biconnected)，簡稱雙連通或重連通。一個圖有橋，當且僅當這個圖的邊連通度為1，則割邊集合的唯一元素被稱為橋(bridge)，又叫關節邊(articulation edge)。

可以看出，點雙連通與邊雙連通都可以簡稱為雙連通，它們之間是有著某種聯系的

[雙連通分支] 

在圖G的所有子圖G’中，如果G’是雙連通的，則稱G’為雙連通子圖。如果一個雙連通子圖G’它不是任何一個雙連通子圖的真子集，則G’為極大雙連通子圖。雙連通分支(biconnected component)，或重連通分支，就是圖的極大雙連通子圖。特殊的，點雙連通分支又叫做塊。

[求割點與橋]

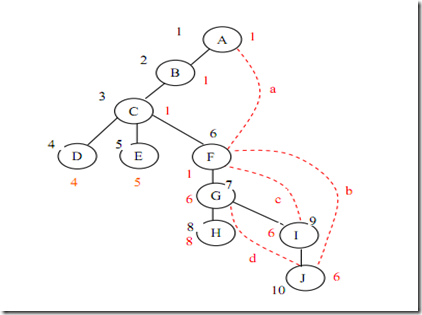
該算法是R.Tarjan發明的。對圖深度優先搜索，定義DFS(u)為u在搜索樹（以下簡稱為樹）中被遍歷到的次序號。定義Low(u)為u或u的子樹中能通過非父子邊追溯到的最早的節點，即DFS序號最小的節點。根據定義，則有：

Low(u)=Min
{
DFS(u)
DFS(v) (u,v)為后向邊(返祖邊) 等價于 DFS(v)<DFS(u)且v不為u的父親節點
Low(v) (u,v)為樹枝邊(父子邊)
}

一個頂點u是割點，當且僅當滿足(1)或(2)
(1) u為樹根，且u有多于一個子樹。
(2) u不為樹根，且滿足存在(u,v)為樹枝邊(或稱父子邊，即u為v在搜索樹中的父親)，使得DFS(u)<=Low(v)。

一條無向邊(u,v)是橋，當且僅當(u,v)為樹枝邊，且滿足DFS(u)<Low(v)。

[求雙連通分支]

下面要分開討論點雙連通分支與邊雙連通分支的求法。

對于點雙連通分支，實際上在求割點的過程中就能順便把每個點雙連通分支求出。建立一個棧，存儲當前雙連通分支，在搜索圖時，每找到一條樹枝邊或后向邊(非橫叉邊)，就把這條邊加入棧中。如果遇到某時滿足DFS(u)<=Low(v)，說明u是一個割點，同時把邊從棧頂一個個取出，直到遇到了邊(u,v)，取出的這些邊與其關聯的點，組成一個點雙連通分支。割點可以屬于多個點雙連通分支，其余點和每條邊只屬于且屬于一個點雙連通分支。

對于邊雙連通分支，求法更為簡單。只需在求出所有的橋以后，把橋邊刪除，原圖變成了多個連通塊，則每個連通塊就是一個邊雙連通分支。橋不屬于任何一個邊雙連通分支，其余的邊和每個頂點都屬于且只屬于一個邊雙連通分支。

[構造雙連通圖]

有橋的連通圖必然有割點，有割點的連通圖不一定有橋(下圖可以很明顯得到)

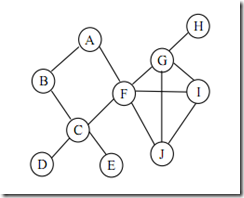
如果一個圖有橋，則把此圖變成無橋的圖的最優策略：

一個有橋的連通圖（其必然有割點），如何把它通過加邊變成邊雙連通圖？方法為首先求出所有的橋，然后刪除這些橋邊，剩下的每個連通塊都是一個邊雙連通子圖。把每個雙連通子圖收縮為一個頂點，再把橋邊加回來，最后的這個圖一定是一棵樹，邊連通度為1。

統計出樹中度為1的節點的個數，即為葉節點的個數，記為leaf。則至少在樹上添加(leaf+1)/2條邊，就能使樹達到邊二連通，所以至少添加的邊數就是(leaf+1)/2。具體方法為，首先把兩個最近公共祖先最遠的兩個葉節點之間連接一條邊，這樣可以把這兩個點到祖先的路徑上所有點收縮到一起，因為一個形成的環一定是雙連通的。然后再找兩個最近公共祖先最遠的兩個葉節點，這樣一對一對找完，恰好是(leaf+1)/2次，把所有點收縮到了一起。

如果一個圖無橋有割點，則把此圖變成雙連通的最優策略：

如果一個圖既有橋，又有割點，則把此圖變成雙連通的策略：（不是最優。。。）

1 首先把圖變成無橋的

2 把有割點無橋的圖變成雙連通

（顯然這個算法不是最優的。。關鍵問題是把圖變成無橋的圖的時候的策略選擇！這個需要高手指點。。。）

A biconnected component (or 2-connected component) in graph theory is a maximalbiconnected subgraph. Any connected graph decomposes into a tree of biconnected components called the block tree of the graph. The blocks are attached to each other at shared vertices called cut vertices or articulation points. Specifically, a cut vertex is any vertex that when removed increases the number of connected components.

算法的基本描述：

The classic sequential algorithm for computing biconnected components in a connected undirected graph due to John Hopcroft andRobert Tarjan (1973) ^[1] runs in linear time, and is based on depth-first search. This algorithm is also outlined as Problem 22-2 of Introduction to Algorithms (both 2nd and 3rd edition).

The idea is to run a depth-first search while maintaining the following information:

1. the depth of each vertex in the depth-first-search tree (once it gets visited), and
2. for each vertex v, the lowest depth of neighbors of all descendants of v in the depth-first-search tree, called thelowpoint.

The depth is standard to maintain during a depth-first search. The lowpoint of v can be computed after visiting all descendants of v (i.e., just before v gets popped off the depth-first-search stack) as the minimum of the depth of all neighbors of v (other than v's parent in the depth-first-search tree) and the lowpoint of all children of v in the depth-first-search tree.

The key fact is that a nonroot vertex v is a cut vertex (or articulation point) separating two biconnected components if and only if v's lowpoint is at least as large as v's depth. This property can be tested once the lowpoint of v is computed (i.e., just before v gets popped off the depth-first-search stack), and if true, v separates the graph into different biconnected components. This can be represented by computing one biconnected component out of the descendants of v (by traversing the depth-first-search tree), and henceforth pretending that v had no children in the depth-first-search tree, so that the subgraph abovev will not descend into v's ancestors.

The root vertex must be handled separately: it is a cut vertex if and only if it has at least two children. Thus, it suffices to simply build one component out of each child subtree of the root (including the root).

Each color corresponds to a biconnected component. Multi-colored vertices are cut vertices, and thus belong to multiple biconnected components.

引入割點的目的： 如果我們去掉圖中的某個點之后，那么這個圖是否還是連通的！

引入2連通分量(塊)的目的：圖的某個子圖是否可以去掉一個點之后，仍然是連通的。也就是說相對于這個子圖，沒有割點。此圖的割含有兩個點。

（注意一個圖的割和割點不是一個概念！）

Reference ：

http://www.byvoid.com/blog/biconnect/         byvoid的NX文章

Wiki 配圖

中科院研究生院算法分析設計講義（陳老師）