看到好朋友zz的一個(gè)ACM總結(jié)，寫(xiě)的非常好。。暫且轉(zhuǎn)載一下把。。。
ACM比賽對(duì)于選手的要求，很簡(jiǎn)單，只有兩點(diǎn)：算法和程序?qū)崿F(xiàn)。
當(dāng)然一些隊(duì)友的配合以及良好的心態(tài)都是一些很隱性的因素，這里只說(shuō)如何提高這兩塊。
算法方面：
第一，要不斷學(xué)習(xí)新算法，擴(kuò)寬自己的知識(shí)面，不要怕難，不要怕麻煩，學(xué)習(xí)是在別人研究的基礎(chǔ)上，如果這點(diǎn)做不好，也很難在更深的層次發(fā)展；
第二，平時(shí)著重培養(yǎng)自己思考問(wèn)題的能力，而不是拘泥在固有的算法和題目里，拿來(lái)一道題目，要有自己的一套思維習(xí)慣，從何入手，如何分析問(wèn)題，思考的軌跡要很清晰的展開(kāi)，這一點(diǎn)，是最核心的，也是最難的；
第三，模板一定要用自己理解后自己寫(xiě)的，只是秉著一副“拿來(lái)主義”，很多自認(rèn)為了解的東西也只是表層的；
第四，不要局限自己的思維，既有的東西雖好，但創(chuàng)新永遠(yuǎn)是樂(lè)趣所在。
程序設(shè)計(jì)方面：
第一，養(yǎng)成良好的編程習(xí)慣，做好一件東西，首先要把他當(dāng)做一種藝術(shù)，程序也是一種藝術(shù)，把自己的程序經(jīng)營(yíng)成可以欣賞的藝術(shù)；
第二，不要在思路不清晰的時(shí)候?qū)懗绦颍砗盟悸罚@也是設(shè)計(jì)的過(guò)程；
第三，不必使用一些高深的語(yǔ)法，多用類(lèi)來(lái)封裝，適當(dāng)?shù)睦肧TL；
第四，寫(xiě)的時(shí)候著重整體，檢查的時(shí)候注意細(xì)節(jié)。
寫(xiě)的非常好，對(duì)自己是一種鼓勵(lì)！！
如果一個(gè)NPC問(wèn)題存在偽多項(xiàng)式時(shí)間算法，那么稱(chēng)其為Weakly NP-Complete。否則，稱(chēng)為Strongly NP-Complete.
很明顯的一個(gè)例子是0-1背包問(wèn)題，這一點(diǎn)經(jīng)常容易引起別人的誤解。其實(shí)0-1背包問(wèn)題是一個(gè)NPC問(wèn)題，你可以簡(jiǎn)單的把它規(guī)約到子集和問(wèn)題，但是有人經(jīng)常爭(zhēng)辯說(shuō)0-1 kanpsack問(wèn)題存在Polynomial Algorithm，那么問(wèn)題就在這里，那個(gè)所謂的Polynomial Algorithm is Pseudo-Polynomial actually！
一個(gè)經(jīng)典0-1背包問(wèn)題的DP解法的時(shí)間復(fù)雜度是O(nW)，W為背包容量，但是背包容量是否需要枚舉[min(…),\sum(…)]呢？所以問(wèn)題就在這里了復(fù)雜度是O(n2^n)…
還有一個(gè)問(wèn)題就是素性檢測(cè)！這個(gè)當(dāng)然也是NPC的了。。
In the case of primality, it turns out there is a different algorithm for testing whether n is prime (discovered in 2002) which runs in time O(log6n).
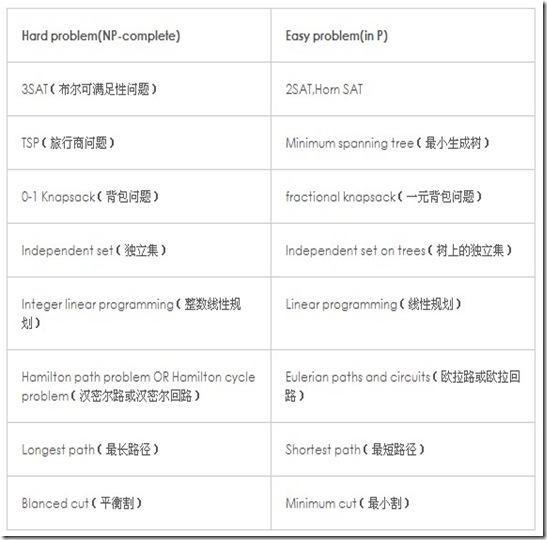
如果仍然不是很清楚，那么需要熟悉一下NPC與P類(lèi)問(wèn)題區(qū)別，下面是一個(gè)不錯(cuò)的表格。。。
不過(guò)貌似在源blog中有一處錯(cuò)誤。。。Linear Programming的確是P問(wèn)題，但是解決這個(gè)P問(wèn)題的simplex 算法卻不是Polynomial的，這個(gè)需要注意！
http://brand.site.co.il/riddles/usingyourhead.html