When the depth-first search reaches a vertex v, the algorithm performs the following steps:
- Set the preorder number of v to C, and increment C.
- Push v onto S and also onto P.
- For each edge from v to a neighboring vertex w:
- If the preorder number of w has not yet been assigned, recursively search w;
- Otherwise, if w has not yet been assigned to a strongly connected component:
- Repeatedly pop vertices from P until the top element of P has a preorder number less than or equal to the preorder number of w.
- If v is the top element of P:
- Pop vertices from S until v has been popped, and assign the popped vertices to a new component.
- Pop v from P.
Gabow_Algorithm偽代碼:
step1:
找一個沒有被訪問過的節(jié)點v，goto step2(v)。否則，算法結(jié)束。
step2(v):
將v壓入堆棧stk1[]和stk2[]
對于v所有的鄰接頂點u：
1) 如果沒有訪問過，則step2(u)
2) 如果訪問過，但沒有刪除，維護stk2[](處理環(huán)的過程，在stk2 中刪除構(gòu)成環(huán)的節(jié)點)
如果stk2[]的頂元素==v，那么輸出相應(yīng)的強連通分量
這個算法其實就是Tarjan算法的變異體，我們觀察一下，只是它用第二個堆棧來輔助求出強連通分量的根，而不是Tarjan算法里面的DFN[]和Low[]數(shù)組。那么，我們說一下如何使用第二個堆棧來輔助求出強連通分量的根。
我們使用類比方法，在Tarjan算法中，每次Low[i]的修改都是由于環(huán)的出現(xiàn)(不然，Low[i]的值不可能變小)，每次出現(xiàn)環(huán)，在這個環(huán)里面只剩下一個Low[i]沒有被改變(深度最低的那個)，或者全部被改變，因為那個深度最低的節(jié)點在另一個環(huán)內(nèi)。那么Gabow算 法中的第二堆棧變化就是刪除構(gòu)成環(huán)的節(jié)點，只剩深度最低的節(jié)點，或者全部刪除，這個過程是通過出棧來實現(xiàn)，因為深度最低的那個頂點一定比前面的先訪問，那 么只要出棧一直到棧頂那個頂點的訪問時間不大于深度最低的那個頂點。其中每個被彈出的節(jié)點屬于同一個強連通分量。那有人會問：為什么彈出的都是同一個強連 通分量？因為在這個節(jié)點訪問之前，能夠構(gòu)成強連通分量的那些節(jié)點已經(jīng)被彈出了，這個對Tarjan算法有了解的都應(yīng)該清楚，那么Tarjan算法中的判斷根我們用什么來代替呢？想想，其實就是看看第二個堆棧的頂元素是不是當前頂點就可以了。
現(xiàn)在，你應(yīng)該明白其實Tarjan算法和Gabow算法其實是同一個思想的不同實現(xiàn)，但是，Gabow算法更精妙，時間更少(不用頻繁更新Low[])。
代碼：
#include "cstdlib"
#include "cctype"
#include "cstring"
#include "cstdio"
#include "cmath"
#include "algorithm"
#include "vector"
#include "string"
#include "iostream"
#include "sstream"
#include "set"
#include "queue"
#include "stack"
#include "fstream"
#include "strstream"
using namespace std;
#define M 2000 //題目中可能的最大點數(shù)
int STACK[M],top=0; //Gabow 算法中的輔助棧
int STACK2[M],top2=0; //
int DFN[M]; //深度優(yōu)先搜索訪問次序
int ComponetNumber=0; //有向圖強連通分量個數(shù)
int Index=0; //索引號
int Belong[M]; //某個點屬于哪個連通分支
vector <int> Edge[M]; //鄰接表表示
vector <int> Component[M]; //獲得強連通分量結(jié)果
void Gabow(int i)
{
int j;
DFN[i]=Index++;
STACK[++top]=i;
STACK2[++top2]=i;
for (int e=0;e<Edge[i].size();e++)
{
j=Edge[i][e];
if (DFN[j]==-1) Gabow(j);
else if (Belong[j]==-1) //如果訪問過，但沒有刪除，維護STACK2
{
while(DFN[STACK2[top2]]>DFN[j]) //刪除構(gòu)成環(huán)的頂點
top2--;
}
}
if(i==STACK2[top2]) //如果Stack2 的頂元素等于i，輸出相應(yīng)的強連通分量
{
--top2; ++ComponetNumber;
do
{
Belong[STACK[top]]=ComponetNumber;
Component[ComponetNumber].push_back(STACK[top]);
}while ( STACK[top--]!=i);
}
}
void solve(int N) //此圖中點的個數(shù)，注意是0-indexed！
{
memset(STACK,-1,sizeof(STACK));
memset(STACK2,-1,sizeof(STACK2));
memset(Belong,-1,sizeof(Belong));
memset(DFN,-1,sizeof(DFN));
for(int i=0;i<N;i++)
if(DFN[i]==-1)
Gabow(i);
}
/*
此算法正常工作的基礎(chǔ)是圖是0-indexed的。但是獲得的結(jié)果Component數(shù)組和Belong數(shù)組是1-indexed
*/
int main()
{
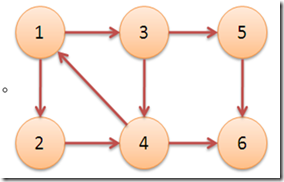
Edge[0].push_back(1);Edge[0].push_back(2);
Edge[1].push_back(3);
Edge[2].push_back(3);Edge[2].push_back(4);
Edge[3].push_back(0);Edge[3].push_back(5);
Edge[4].push_back(5);
int N=6;
solve(N);
cout<<"ComponetNumber is "<<ComponetNumber<<endl;
for(int i=0;i<N;i++)
cout<<Belong[i]<<" ";
cout<<endl;
for(int i=0;i<N;i++)
{
for(int j=0;j<Component[i].size();j++)
cout<<Component[i][j];
cout<<endl;
}
return 0;
}
Reference：
http://rchardx.is-programmer.com/posts/14898.html
wiki
終于搞完了SCC問題的3大算法：
小總結(jié)一下：
三種算法的時間復(fù)雜度都是O(M+N) （N為圖的點數(shù)，M為邊數(shù)）
Tarjan 算法和Gabow算法思想類似，在Tarjan算法中用Low[]數(shù)組來記錄所能達到的最小時間戳，而Gabow算法則是用Stack2[]輔助獲得了強連通分量的根！
二者實質(zhì)是一樣的！
Kosaraju 算法則是兩次DFS，所以在時間復(fù)雜度常數(shù)因子的比拼上，肯定拼不過 Tarjan Gabow，但是額外的常數(shù)帶來了良好的拓撲性質(zhì)！它得到的節(jié)點是按照拓撲序組織好的，在求解2-SAT的過程中十分方便。
下面是題目來總結(jié)或者來一個求無向圖雙連通分量Tarjan算法 和求最近公共祖先的離線Tarjan算法！
再引用一次：
Tarjan算法與求無向圖的雙連通分量(割點、橋)的Tarjan算法也有著很深的聯(lián)系。學(xué)習(xí)該Tarjan算法，也有助于深入理解求雙連通分量的Tarjan算法，兩者可以類比、組合理解。
求有向圖的強連通分量的Tarjan算法是以其發(fā)明者Robert Tarjan命名的。Robert Tarjan還發(fā)明了求雙連通分量的Tarjan算法，以及求最近公共祖先的離線Tarjan算法，在此對Tarjan表示崇高的敬意。