1 隨機(jī)化算法優(yōu)點(diǎn):
Best
Speed
Simplicity
Derandomization
Adversary argumetns and lower bounds
這個(gè)和沒說一樣。�����。
2 Randomized Algorithms 與average case analyasis的不同點(diǎn)���。這個(gè)也是顯然
3 快速排序的比較次數(shù)分析
<=n +2nln(n)
分析使用的技巧相當(dāng)相當(dāng)牛�!
4 BSP問題:
Binary space partitioning (BSP) is a method for recursively subdividing a space into convex sets by hyperplanes. This subdivision gives rise to a representation of the scene by means of a tree data structure known as a BSP tree.
Originally, this approach was proposed in 3D computer graphics to increase the rendering efficiency. Some other applications include performing geometrical operations with shapes (constructive solid geometry) in CAD, collision detection in robotics and 3D computer games, and other computer applications that involve handling of complex spatial scenes.
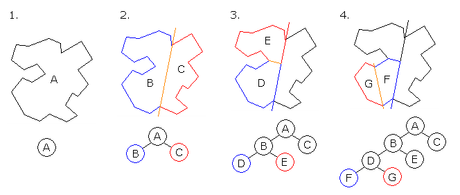
1. A is the root of the tree and the entire polygon
2. A is split into B and C
3. B is split into D and E.
4. D is split into F and G, which are convex and hence become leaves on the tree.
看一下這個(gè)圖,不用介紹大概也明白了���。。但是�,我們需要多少次操作呢�����。。作者又進(jìn)行了概率分析�。�。2*n *H(n) Harmonic Number還真是哪里都有���。�。服了�����。�����。
Other space partitioning structures其他的空間劃分的數(shù)據(jù)結(jié)構(gòu)
BSP trees divide a region of space into two subregions at each node. They are related to quadtrees and octrees, which divide each region into four or eight subregions, respectively.
Relationship Table
Name
p
s
Binary Space Partition
1
2
Quadtree
2
4
Octree
3
8
where p is the number of dividing planes used, and s is the number of subregions formed.
BSP trees can be used in spaces with any number of dimensions, but quadtrees and octrees are most useful in subdividing 2- and 3-dimensional spaces, respectively. Another kind of tree that behaves somewhat like a quadtree or octree, but is useful in any number of dimensions, is the kd-tree.
教程很新穎,雖然在北美開randomized Algorithms已經(jīng)很多年了���。。但是貌似在中國(guó)還沒聽說過這課程�����。�。
利用概率分析的相當(dāng)透徹。。把QuickSort和BSP數(shù)開始�����,進(jìn)行了隨機(jī)化過程中的比較次數(shù)的期望分析�����。�。方法很新穎�!
我用的這個(gè)講義是UIUC 08的。���。此外Berkerly 和CMU也有這門課程。�。教材是那本盡人皆知的Randomized Algorithms�。�����。。大牛?。�����。?/p>