今天保研的小朋友來所里筆試+面試。。。。全國各大名牌高校都往這里擠啊。。。
有序立方體
問題描述:
給定一個由N個互不相同的整數(shù)構(gòu)成的序列{x0, x1, ..., xN-1 },如果其元素是按照升序排列的:x0 < x1 < ... < xN-1,那么我們稱之為有序數(shù)列
類似地,如果一個N x N的二維數(shù)組滿足它的所有行和所有列都是有序數(shù)列的話,那么它就是一個有序平面。
于是我們可以定義一個N x N x N的三維數(shù)組為有序立方體,如果它垂直于三個軸向的所有截面都是有序平面。如下圖所示,z = 0定義了立方體垂直于z軸的頂截面,而z = N – 1則定義了立方體垂直于z軸的底截面。在本題中,1到N3的所有整數(shù)均出現(xiàn)且僅出現(xiàn)一次。
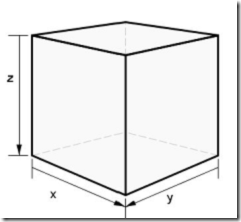
要求編寫函數(shù)sortCube,使其以盡量少的交換次數(shù)將初始立方體變換為有序立方體。
輸入?yún)?shù):
? int N表示立方體每個維度的尺寸大小;
? int initCube[N*N*N]為初始立方體配置,按照平面優(yōu)先和行優(yōu)先的順序?qū)⑷S數(shù)組表示為一維向量,即立方體中坐標(biāo)(X, Y, Z)的數(shù)據(jù)在initCube中的索引值為N*N*Z + N*Y + X;。
輸出參數(shù):
? 按照"X1,Y1,Z1-X2,Y2,Z2"的格式輸出所需交換操作步驟。這里'X1', 'Y1', 'Z1', 'X2', 'Y2', 'Z2'表示0到N-1之間的數(shù)據(jù)下標(biāo),而每一個元素則表示互換(X1, Y1, Z1)與(X2, Y2, Z2)位置的數(shù)據(jù)。
這里給出我的想法吧:
首先給出一個定義,在原點處我們假設(shè)其坐標(biāo)為(0,0,0)。對于3*3*3立方體,從一個很顯然的角度來說,把立方體沿著對角線立起來。。我們可以注意到這個立方體可以被分為很多層,第一層是(0,0,0)第二層是(0,0,1)(1,0,0)(0,1,0),第三層是(0,0,2)(2,0,0)(0,2,0)(1,0,1)(1,1,0)(0,1,1),這樣子可以擴展地想一下,總共可以分為7層,這七層中可以用曼哈頓距離分類:
距離: 0 1 2 3 4 5 6
點數(shù): 1 3 6 7 6 3 1
總共有27個點了。。。
如果擴展到n*n*n的話,我們依然使用 曼哈頓距離來分類。假設(shè)n無限大的話,
在第n層中會有幾個點呢?這個可以等價到這樣一個問題,x+y+z=n
x>=0 y>=0 z>=0 的正整數(shù)解的個數(shù)。這個問題高中生都會。。。。
等價于從n+2個物品中選擇2個。。。C(2,n+2)
然后對于一個給定的n,我們究竟有多少層呢?。。。簡單的觀察就知道,前后對稱。。
以此正方體體對角線開始減1 3 。。。直至構(gòu)造到(0,0,N-1),此時停止構(gòu)造。。這個時候,上面推導(dǎo)的那個公式C(2,n+2)就不對了。。此時剩余了多少層呢?。。。同樣的哈密頓距離告訴我們N層。。。那么這n層怎么搞呢?
x+y+z=M
N>x>=0 N>y>=0 N>z>=0 就是這樣一個方程。。。M的范圍在[0,3*N-1]。。。有想法了吧?!
下面將是這個問題的核心部分,也是最精彩的部分。。。給出了3*N層,把它抽象成一個3*N個點的圖。。遍歷給定的一個特殊的立方體,判斷相應(yīng)位置中的數(shù)是屬于那一層的。如果屬于該層,當(dāng)然不用什么交換了之類的操作,如果不屬于,把當(dāng)前層的點與它隸屬層的點連接一條有向邊,指向它的目標(biāo)層。遍歷操作結(jié)束,就構(gòu)造成了一張圖!
有點眉目了么?沒錯,就是置換群的變種!此時,我們只要在圖中尋找回路,然后求得回路的邊數(shù),一個回路組成一個置換群。答案就是所有回路邊數(shù)-回路數(shù)。。。。
的確是很bug的一道題目。。去年的這個時候看過這個題目。。沒有想出解答方案。。當(dāng)然面試的時候比較簡單。。直接是求出一個方案,沒必要要求最小。。。今天終于想到了一個解決方案。。。問題的思考是慢慢的一步一步的。。。