棋盤分割
Time Limit:1000MS? Memory Limit:10000K
Total Submit:490 Accepted:194
Description
將一個８*８的棋盤進行如下分割：將原棋盤割下一塊矩形棋盤并使剩下部分也是矩形，再將剩下的部分繼續如此分割，這樣割了(n-1)次后，連同最后剩下的矩形棋盤共有n塊矩形棋盤。(每次切割都只能沿著棋盤格子的邊進行)
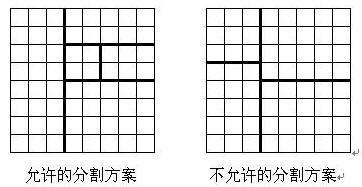
原棋盤上每一格有一個分值，一塊矩形棋盤的總分為其所含各格分值之和。現在需要把棋盤按上述規則分割成n塊矩形棋盤，并使各矩形棋盤總分的均方差最小。
均方差
，其中平均值
，xi為第i塊矩形棋盤的總分。
請編程對給出的棋盤及n，求出O'的最小值。
Input
第1行為一個整數n(1 < n < 15)。
第2行至第9行每行為8個小于100的非負整數，表示棋盤上相應格子的分值。每行相鄰兩數之間用一個空格分隔。
Output
僅一個數，為O'（四舍五入精確到小數點后三位）。
Sample Input
3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 3
Sample Output
1.633
Source
Noi 99
#include?
<
iostream
>
#include?
<
cstdlib
>
#include?
<
cmath
>
using
?
namespace
?std;
const
?
int
?INF?
=
?
2000000000
;
int
?f[
9
][
9
][
9
][
9
][
15
];
int
?s[
9
][
9
][
9
][
9
];
int
?d[
9
][
9
];
void
?init()
{
????
int
?x1,?y1,?x2,?y2;
????
int
?i,?j;
????
int
?sum;
????
for
?(x1
=
1
;?x1
<=
8
;?x1
++
)
????????
for
?(y1
=
1
;?y1
<=
8
;?y1
++
)
????????????
for
?(x2
=
x1;?x2
<=
8
;?x2
++
)
????????????????
for
?(y2
=
y1;?y2
<=
8
;?y2
++
)
????????????????
{
????????????????????sum?
=
?
0
;
????????????????????
for
?(i
=
x1;?i
<=
x2;?i
++
)
????????????????????????
for
?(j
=
y1;?j
<=
y2;?j
++
)
????????????????????????????sum?
+=
?d[i][j];
????????????????????s[x1][y1][x2][y2]?
=
?sum;
????????????????????f[x1][y1][x2][y2][
1
]?
=
?sum?
*
?sum;
????????????????}
}
int
?main()
{
????
int
?n;
????
int
?i,?j,?k;
????
int
?x1,?y1,?x2,?y2;
????
int
?a,?b;
????
int
?t,?tmp;
????
double
?p?
=
?
0
;
????scanf(
"
%d
"
,?
&
n);
????
????
for
?(i
=
1
;?i
<=
8
;?i
++
)
????????
for
?(j
=
1
;?j
<=
8
;?j
++
)
????????
{
????????????scanf(
"
%d
"
,?
&
d[i][j]);
????????????p?
+=
?d[i][j];
????????}
????p?
/=
?n;
//
????cout?<<?"???"<<?p?<<?endl;
????init();
????
for
?(k
=
2
;?k
<=
n;?k
++
)
????
{
????????
for
?(x1
=
1
;?x1
<=
8
;?x1
++
)
????????????
for
?(y1
=
1
;?y1
<=
8
;?y1
++
)
????????????????
for
?(x2
=
x1;?x2
<=
8
;?x2
++
)
????????????????????
for
?(y2
=
y1;?y2
<=
8
;?y2
++
)
????????????????????
{
????????????????????????tmp?
=
?INF;
????????????????????????
//
豎切
????????????????????????
for
?(a
=
x1;?a
<
x2;?a
++
)
????????????????????????
{
????????????????????????????t?
=
?min(f[x1][y1][a][y2][k
-
1
]
+
s[a
+
1
][y1][x2][y2]
*
s[a
+
1
][y1][x2][y2]
????????????????????????????????,?f[a
+
1
][y1][x2][y2][k
-
1
]
+
s[x1][y1][a][y2]
*
s[x1][y1][a][y2]);
????????????????????????????
if
?(tmp?
>
?t)?
????????????????????????????????tmp?
=
?t;
????????????????????????}
????????????????????????
//
橫切
????????????????????????
for
?(b
=
y1;?b
<
y2;?b
++
)
????????????????????????
{
????????????????????????????t?
=
?min(f[x1][y1][x2][b][k
-
1
]
+
s[x1][b
+
1
][x2][y2]
*
s[x1][b
+
1
][x2][y2]
????????????????????????????????,?f[x1][b
+
1
][x2][y2][k
-
1
]
+
s[x1][y1][x2][b]
*
s[x1][y1][x2][b]);
????????????????????????????
if
?(tmp?
>
?t)
????????????????????????????????tmp?
=
?t;
????????????????????????}
????????????????????????
????????????????????????f[x1][y1][x2][y2][k]?
=
?tmp;
????????????????????}
????}
????printf(
"
%.3f\n
"
,?sqrt(
double
(f[
1
][
1
][
8
][
8
][n])
/
double
(n)
-
p
*
p));
????
return
?
0
;
}
posted on 2006-09-08 22:57
豪 閱讀(1318)
評論(0) 編輯 收藏 引用 所屬分類:
ACM題目