如何���定中文字符串的�怼��?/span>
作者:肖�L
个�h博客�Q?/span>http://blog.csdn.net/eaglet
Email�Q?a href="mailto:blog.eaglet@gmail.com">blog.eaglet@gmail.com
2007/4 南京
摘要
在数据挖掘的研究中,我们往往需要判断文章是否雷�?/span>,对类似文章或短句�q�行归类处理�{�,�q�其中就会遇到这��L��问题�Q�如何确定两个字�W�串之间的相似程度�?/span>
本文�l�合作者的实际工作�l�验和数据挖掘理论,�l�合中文字符串特性介�l�一套相对完整的�Ҏ���Q�以解决上述问题.�?/span>
分析
最���单的问题求解
字符串由一�l�不同含义的单词�l�成�Q�它不同于数值型变量�Q�可以用一个特定的数值来���定它的大小或位�|�,所以用何种方式来描�q�C��个字�W�串之间的距���,成�ؓ了一个值得探讨的问题�?/span>
通常情况下,用于分析的数据类型有如下几种�Q�区间标度遍历、二元变量、标�U�型变量、序数型变量、比例标度型变量、�合类型变量等�?/span>
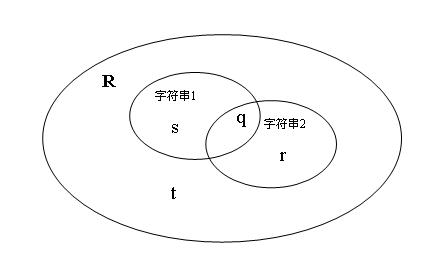
�l�合�q�些变量�c�d���Q�本文认为字�W�串变量更适合于归�c�M��二元变量�Q�我们可以利用分词技术将字符串分成若�q�个单词�Q�每个独立的单词作�ؓ二元变量的一个属性。我们把所有单词设定�ؓ一个二元变量属性集�?/span>R�Q�字�W�串1和字�W�串2的单词包含于�q�个集合R。设q是字�W�串1和字�W�串2中都存在的单词的��L���Q?/span>s是字�W�串1中存在,字符�?/span>2中不存在的单词��L���Q?/span>r是字�W�串2中存在,字符�?/span>1中不存在的单词��L���Q?/span>t是字�W�串1和字�W�串2中都不存在的单词��L��。我们称 q,r,s,t为字�W�串比较中的4个状态分量�?/span> 如图1所�C�:
�׃��两个字符串都不存在的单词对两个字�W�串的比较没有�Q何作用,所以忽�?/span>t�Q�于是我们采用非恒定的相似度评�h�p�L��(Jaccard�p�L��)来描�q�C��个字�W�串见的相异度表�C�公式�ؓ
相异�?/span> = r+s / (q+r+s)�Q�不难推断,他们的�Ş似度公式�?/span>
�怼��?/span>=q/(q+r+s) 公式1
�?/span>1 字符串关�p�L���q?/span>
例如如下两个字符串串�Q?/font>
字符�?/span>1�Q�非对称变量
字符�?/span>2�Q�非对称�I�间
他们的二元属性关�p�表为:
|
字符�?/span>/属�?/span>
|
�?/font>
|
对称
|
变量
|
�I�间
|
|
非对�U�变�?/font>
|
Y
|
Y
|
Y
|
N
|
|
非对�U�空�?/font>
|
Y
|
Y
|
N
|
Y
|
Y 表示存在该单词属性,N表示不存在该单词属�?/span>
那么对应�?/font>
s = 1; q = 2; r = 1
两个字符串的�怼�度�ؓ 2/(1+2+1) = 50%
单词重复问题求解
前面讨论的问题是最���单的字符串比较问题,�q�个问题中单个字�W�串不存在重复的单词�Q�然而如果字�W�串中出现重复单词,采用上一节的公式套用后得到的�l�果往往不够理想�Q�比�?/font>
字符�?/span>1�Q�前�q�前�q?/span>
字符�?/span>2�Q�前�q?/span>
公式1�怼��?/span>=q/(q+r+s) 来计���,
q = 1 , r=s=0 �Q�得到的�怼�度�ؓ100%�Q�而实际上�q�两个字�W�串�q�不完全相同。�ؓ解决�q�个问题�Q�我们必���d��在不同位�|�出现的相同单词假设��Z��同单词,以其在字�W�串中出现的�ơ序作�ؓ区分�Q�这样其二元属性关�p�表如下�Q?/span>
|
字符�?/span>/属�?/span>
|
前进1
|
前进2
|
|
前进前进
|
Y
|
Y
|
|
前进
|
Y
|
N
|
相应�?/span> q = 1, s=1, r= 0
其相似度�?/span> 1/(1+1+0) = 50%
状态分量权�?/span>
在实际应用中�Q?/span>q,r,s三种状态分量�ƈ不一定是同等价值的�Q�它们往往�Ҏ��实际应用的需要存在不同的权重�Q�比如对于某些应用来��_��两个字符串中相同单词数量比不同单词数量更能说明字�W�串的相似程度,那么我们必须��?/span>q的权重提高,重新计算�怼��E�度�?/span>
我们讑֯��?/span>q,r,s三个变量的权重分别是Kq, Kr, Ks �Q�则公式1 演进�?/span>
�怼��?/span>=Kq*q/(Kq*q+Kr*r+Ks*s) (Kq > 0 , Kr>=0,Ka>=0) 公式2
回到上面问题�Q�对于上一节的两个字符�Ԍ��如果我们讄���Kq = 2 ,Kr=Ks=1�Q�则更加公式2
它们的相似度�?/span> 2*1/ (2*1+1*1+1*0) = 66.7%
同义词问�?/span>
在语�a�中,同义词是�l�常遇到的问题,如果两个字符串中存在同义词,其相似度又如何计���呢�?/font>
对于同义词问题,我们要从分词�q�程中来解决。首先我们需要构��Z��个同义词对照表,���同义词对应��C��个等价单词,在对字符串分词后对字�W�串中的所有单词到同义词表中查找,如果存在�Q�则替换为对应的�{��h单词�Q�这样分词后�Q�两个字�W�串中的同义词就指向了相同的单词�?/font>
比如存在同义词表如下�Q?/font>
|
单词
|
�{��h�?/font>
|
|
也许
|
也许
|
|
或许
|
也许
|
|
可能
|
也许
|
字符�?/span>1�Q�他也许不来�?/span>
字符�?/span>2�Q�他可能不来�?/span>
分词后二元属性关�p�表如下�Q?/font>
|
字符�?/span>/属�?/span>
|
�?/font>
|
也许
|
不来
|
�?/font>
|
|
他也�怸�来了
|
Y
|
Y
|
Y
|
Y
|
|
他可能不来了
|
Y
|
Y
|
Y
|
Y
|
不难看出�Q�两个字�W�串的相似度�?/span> 100%
同音不同�?/span>
在中文网�l�环境中�Q�由于大多数�|�络文章的作者都是采用拼韌���入法输入汉字�Q�经�怼�出现输入同音不同义的文字错误�Q��ؓ了纠正这�U�错误,我们可以考虑采用汉语拼音的方式进行分词,也可以综合分词,也就是先正常分词�Q�在拼音分词�Q�字�W�串的分词结果去两者的�q�����?/font>
���节
���定字符串相似度的方法很多,本文�Ҏ��作者多�q�从事数据挖掘工作的�l�验�l�合数据挖掘理论提出的相兌�����x��案,可以较好的解决中文字�W�串分析中的�怼�度比较问题。但技术的发展是不断前�q�的�Q�相信未来还会有更好的方法来解决中文字符串相似度比较问题。读者如果有更好的想法或者发现本文算法中的不���I��非常�Ƣ迎和本文作者联�p�R�?/font>
参考文�?/font>
《数据挖掘概念与技术�?/span> 机械工业出版�C?/span> Jiawei Han, Micheline Kamber

]]>